Wie wir im vorherigen Kapitel betrachtet haben, spricht vieles für einen kosmischen Wirbel, der im Zentrum unseres Universums rotiert. Einige Wissen­schaftler sprechen auch von einem kosmischen String, ein langes schweres Objekt mit einem winzigen Quer­schnitt, wie es während der Frühphase des Universums entstanden sein könnte. Dieser Kosmos­wirbel hat einen Gesamt­drehimpuls, der sich maßgeblich auf die von ihm umgebenen Strukturen auswirkt. Dieser Wirbel im Zentrum ist im Grunde die „Mutter” aller Schwarzen Löcher.

Abb. 1: Schwarzes Loch (© NASA/JPL-Caltech)

Schwarze Löcher bringt man im Allgemeinen mit einer Supernova in Verbindung. Hat z. B. ein Protostern am Ende seines Lebens­zyklus eine Masse von mehr als 8 Sonnen­massen, dann kollabiert der Rote Riese nicht zu einem Neutronen­stern, sondern zu einem „Schwarzen Loch”, weil die Gravita­tion im Innern viel stärker ist. Ein Schwarzes Loch ist letzt­lich ein durch die Geometrie verzerrter Raum. Der „Ereignis­horizont” definiert, ab welchem Punkt das Licht noch ent­weichen kann und wann nicht mehr. Bei 8 Sonnen­massen würde der Radius des Ereignis­horizonts beispiels­weise 24 km betragen (R = 3 km × Masse / Sonnenmasse).

Sobald die Photonen den Ereignis­horizont über­schritten haben, reicht ihre Energie nicht mehr aus, um den gekrümmten Raum zu verlassen. Daher kann das Licht nicht mehr zu uns gelangen und wird quasi von dem Schwarzen Loch geschluckt.

Jedes Schwarze Loch zeichnet sich vereinfacht betrachtet durch drei Eigen­schaften aus. Es hat eine extrem große Masse, es besitzt nach wie vor einen Dreh­impuls und es verfügt über Ladung. Alle anderen Eigen­schaften gehen während des Kollapses scheinbar verloren. Aller­dings darf man dabei nicht über­sehen, dass es nach Über­schreiten des Ereignis­horizonts nach wie vor Quanten­zustände gibt. Somit endet nicht alles in einer Singularität.

Die nachfolgende künstlerische Darstellung zeigt die Zentral­region einer aktiven Galaxie, über die Materie spiral­förmig in das super­massereiche Schwarze Loch im Zentrum einströmt. Ein energie­reicher, durch starke Magnet­felder gebündelter Radiojet, wird senkrecht zur Scheibe abgestrahlt. Innerhalb des Jets werden nicht nur Radio-, sondern auch Gamma­photonen erzeugt.

Abb. 2: Schnell rotierendes Schwarzes Loch, das Materie ansammelt. (© NASA/JPL-Caltech)

Um den weiteren Gedanken­gang bezüglich der spiralförmigen Strukturen in den Galaxien nach­vollziehen zu können, müssen wir einen kurzen Sprung zu den kleinsten Strukturen des Lebens machen.

Fast jede Zelle unseres Körpers trägt die Information für den Bau unseres gesamten Körpers in sich. Diese Erbinformation ist im Zell­kern in der DNA, auch „DNS” genannt, gespeichert.

Die DNA ist ein Makromolekül, in welchem die Informationen zur Entwicklung und Funktion des Lebe­wesens kodiert werden. Jeder Abschnitt der DNA, der für ein bestimmtes Protein kodiert, wird als Gen bezeichnet. Im Grunde ist die DNA der Bauplan für die Herstellung von Proteinen.

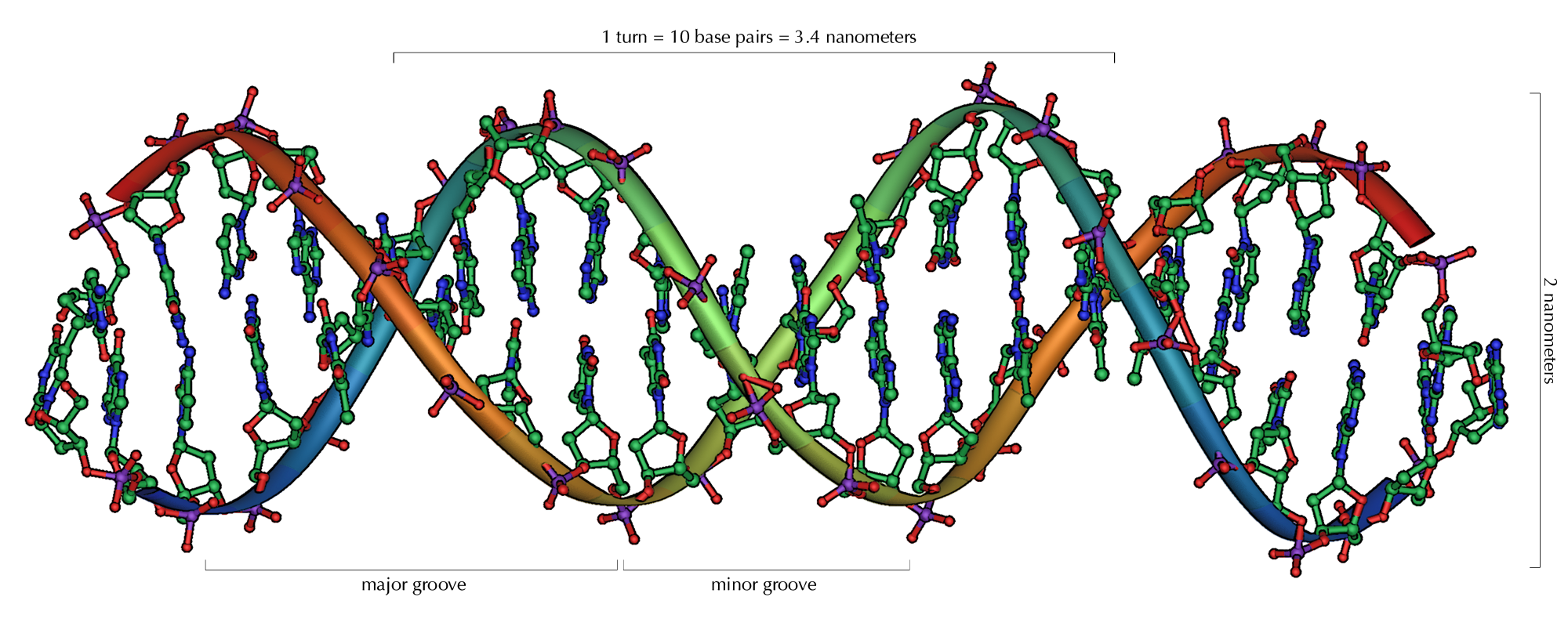
Die Bausteine der DNA sind die sogenannten Nukleotide, die unter anderem aus einer von vier organischen Basen besteht, wobei sich die Nukleotide aneinander­reihen und lange Ketten bilden können. DNA-Moleküle bestehen aus zwei solchen Ketten, die umeinander gewunden sind und damit eine Doppelhelix bilden.

Abb. 3: Der DNA-Strang mit seiner „Doppelhelix”. (BY-SA 3.0)

Diese zwei umeinander gewundenen Ketten, auch „DNA-Stränge” genannt, werden dadurch zusammen­gehalten, dass sich Basen von dem einen Strang mit den Basen vom dem anderen Strang bleibend verbinden. Vereinfacht kann man sich die DNA wie eine Wendel­treppe vorstellen.

Jede Zelle enthält fast zwei Meter DNA! Doch damit die DNA in den winzigen Zellen Platz hat, wird sie fest aufgewunden und raum­sparend in sogenannte Chromosomen verpackt.

Was uns in diesem Zusammen­hang besonders interessiert, ist die „Doppel­helix”. Die zwei Stränge winden sich um eine imaginäre Zentral­achse. Damit die DNA raumsparend und zugleich zerreißsicher verpackt werden kann, muss sich diese Struktur im Raum winden können. Diesen Aspekt zu verstehen ist wichtig, um ihn auf den Kosmos über­tragen zu können.

Nehmen wir an, es würden sich nicht nur 2 sondern z. B. 5, oder unzählbar viele Stränge um eine solche Zentral­achse winden, wobei die Bahn­kurven die Bewegungs­richtung der Galaxien veranschaulichen sollen. Diese Galaxien winden sich im weiteren Verlauf entlang des kosmischen Zeit­strahls, der im Grunde mit der Zentral­achse der DNA vergleichbar wäre.

Eine Galaxie würde also in unserem Beispiel in einem solchen Strang bzw. Bahnkurve rotieren, während der Strang selbst, wie bei der Doppelhelix, um den kosmischen Zeit­strahl driftet. Quasi ähnlich wie bei unserem Sonnen­system. Während das Sonnen­system um das Zentrum der Galaxie rotiert, kreist es mit einem anderen Drehimpuls um die Sonne.

Abb. 4: Beispiel − 5 Galaxien driften durch den gekrümmten Raum.

Alle Galaxien rotieren letzt­endlich um das kosmische Zentrum unseres Universums. Während die Galaxien durch den 4-dimensionalen gekrümmten Raum mit einer Drift ihre Bahnen ziehen, rotieren sie mit einem von ihrem Umfeld abhängigen Dreh­impuls um das jeweilige galaktische Zentrum. Wie wir später noch sehen werden, kann die Rotations­richtung entlang einer solchen Bahn­kurve durchaus variieren. Denn schließlich gibt es Galaxien, die sich links herum drehen und andere, die sich rechts herum drehen.

Abb. 5: Die Galaxien rotieren um den kosmischen Zeitstrahl.

Die Gesamtzahl der Galaxien ist im Kosmos unter­schiedlich verteilt. Es gibt Bereiche, wo die Dichte­verteilung etwas offener ist, wobei es in anderen Bereichen zu sogenannten „Galaxie­haufen” kommt. Dennoch ist unser Universum eine unberandete Mannig­faltigkeit, und die Ausmaße unseres Universums sind trotz seiner gigantischen Größe nicht unendlich.

Des Weiteren ist unser Universum entgegen vorherrschender Meinungen nicht völlig homogen und somit anisotrop. Mit anderen Worten, die Geometrie und die damit verbundene Krümmung des Raums führen im Universum zu unterschiedlichen Expansionsraten, wenngleich vom kosmischen Zeit­strahl im Zentrum aus betrachtet, es in alle Richtungen aufgrund der Spiral­geometrien ähnlich strukturiert aussieht. Die zuvor erwähnten Bahn­kurven der Galaxien sind somit eingebettet im 4-dimensionalen gekrümmten Raum.

Abb. 6: Die Galaxien eingebettet im 4-dimensionalen gekrümmten Raum.

Spiralgalaxien tragen nicht ohne Grund diesen Namen, denn die in ihnen enthaltenen Massen spiralen Richtung Zentrum der Galaxie. Wobei sich jede Galaxie durch eine mitunter abweichende Anzahl von Spiral­armen und eine unter­schiedliche Dreh­richtung auszeichnen kann. Die Anordnung der Spiral­arme, egal ob enganliegend oder weit gefächert, gibt Rück­schlüsse auf den Gesamt­drehimpuls und in welcher Lebens­phase sich eine solche Galaxie befindet.

Nun haben wir bei den Spiral­kurven schon kennen­gelernt, das die Form einer Spirale von der Steigung und von der Krümmung abhängt. Beide Faktoren sind eng miteinander verknüpft und werden bei rotierenden Systemen vom Dreh­impuls beeinflusst. Daher untersuchen wir als Nächstes die Spiral­arme in einer Galaxie etwas genauer.

Jede Galaxie, die wir mithilfe von Teleskopen beobachten, ist im Raum geneigt. Das heißt, wir schauen nie lotrecht auf die Akkretions­scheibe, sondern immer unter einem individuellen Winkel. Um dies zu verdeutlichen, nehmen wir im Nach­folgenden die Whirlpool-Galaxie M51 als Grund­lage, weil man an ihr sehr schön die Spiral­arme erkennen kann. Um die Betrachtung nach­vollziehen zu können, muss man jedoch über etwas räumliches Vorstellungs­vermögen verfügen.

Abb. 7: Whirlpool Galaxy M51 (NGC 5194) (© NASA/JPL-Caltech)

Im ersten Schritt wird auf die ausgewählte Galaxie, in diesem Fall die Whirlpool-Galaxie, ein Koordinaten­kreuz gezeichnet und anschließend ein konzentrischer Kreis projiziert, dessen Radius in etwa den maximalen Abmessungen der Galaxie entspricht.

Gleich­zeitig zeichnen wir die erkennbare Anzahl der Spiral­arme ein, in diesem Fall zwei. Als Grund­lage für die Spiral­arme dient generell die Logarithmische Spirale, wobei die Steigung und die Krümmung zunächst nur grob ausgerichtet werden.

Zusätzlich wird im Koordinaten­ursprung eine z-Achse eingezeichnet, dessen Länge hier einem 1/4 des Kreis­durchmessers entspricht und in der nach­folgenden Grafik lotrecht steht, wobei sie in den anderen Grafiken räumlich mitwandert.

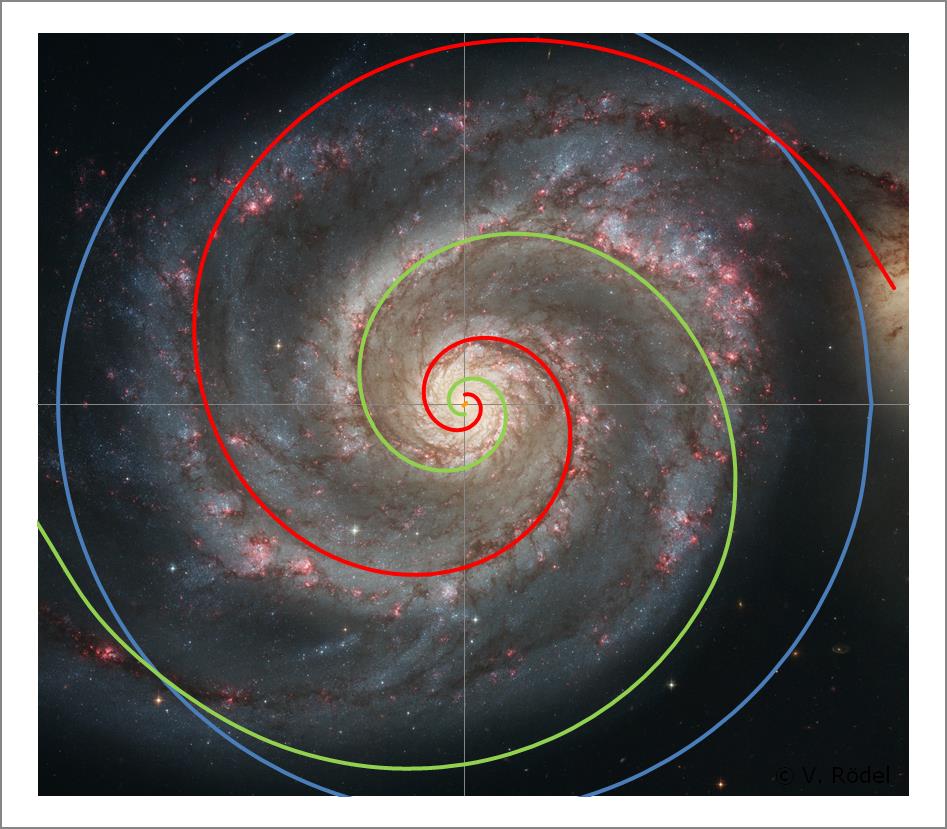
Abb. 8: Ein konzentrischer Kreis mit zwei Spiralarmen.

Im zweiten Schritt drehen wir die Spiral­kurven jetzt um den Koordinaten­ursprung 0, 0, in diesem Fall um ca. 15° gegen den Uhrzeiger­sinn. Die x-Achse passt sich entsprechend dem Dreh­winkel an.

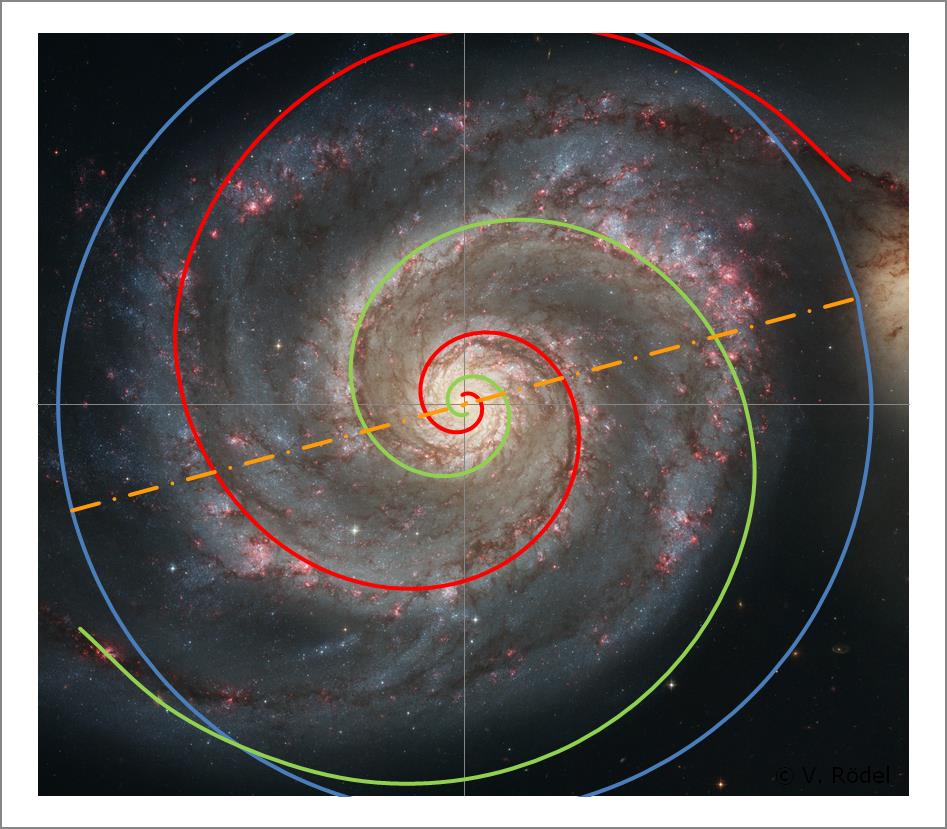
Abb. 9: Um die z-Achse gedrehte Spiralarme.

Im dritten Schritt schwenken wir den Kreis mitsamt den Spiral­armen um die x-Achse im Verhältnis zum vermeintlichen Betrachtungs­winkel, sodass der Kreis gestaucht wird und der Beobachter jetzt eine Ellipse wahrnimmt. Mithilfe eines mathe­matischen Berechnungs­tools sind alle Grafiken miteinander verknüpft. Die Steigung und die Krümmung der Spiral­arme passen sich entsprechend den Schwenk- und Dreh­winkeln an. Man kann schon erkennen, wie sich dementsprechend die Bahn­kurven der Spiral­arme der elliptischen Darstellung angleichen.

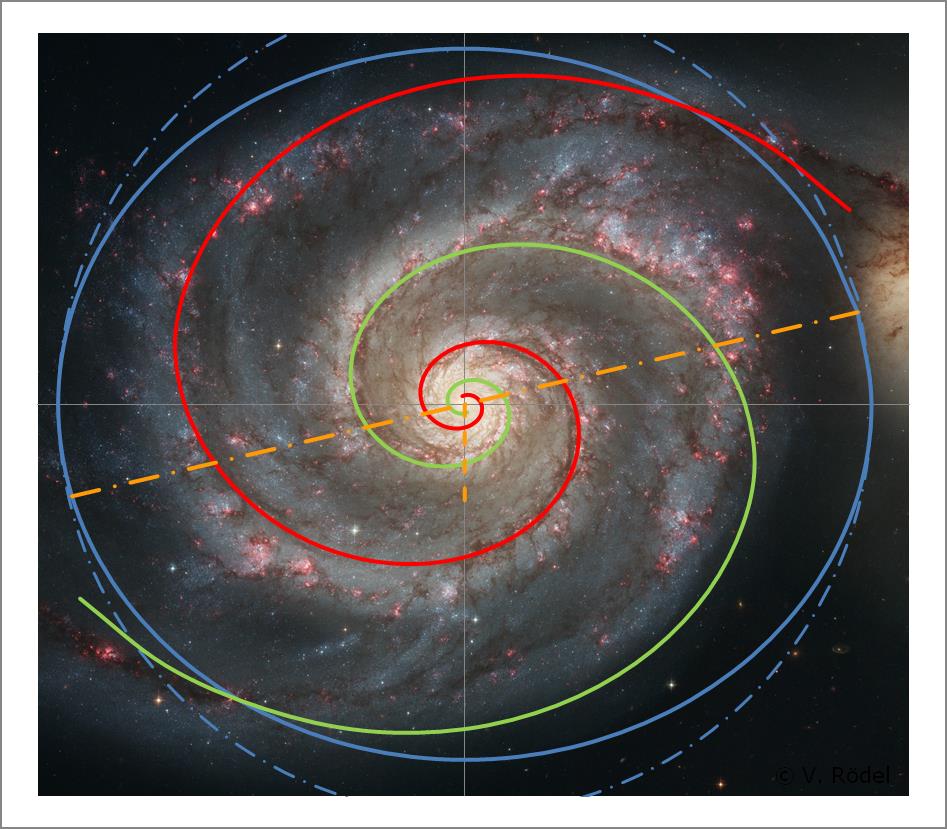
Abb. 10: Um die x-Achse geschwenkte Spiralarme.

Durch diese Vorgehens­weise, die sich übrigens auf jede beliebige Grafik über­tragen lässt, erhält man einen Eindruck, wie die Spiral­arme real aussehen, so als wenn man genau lotrecht auf die Galaxie schauen würde. Bezogen auf die Whirlpool-Galaxie beträgt der Schwenk­winkel um die x-Achse ca. 30°.

Wenn die Spiral­arme nahezu deckungs­gleich mit der Grafik sind, geben die Referenz­werte, die sich aus der Berechnung ergeben, Rück­schlüsse auf den Gesamt­drehimpuls der jeweiligen Galaxie.

Im vierten Schritt könnte man die bereits gedrehte und geschwenkte Projektion nochmals um die y-Achse drehen. Bezogen auf die Whirlpool-Galaxie ist der optische Effekt zwar nur marginal. Um die Auswirkung dennoch zu verdeutlichen, wurde die Projektion in diesem Fall um ca. 15° um die y-Achse gedreht.

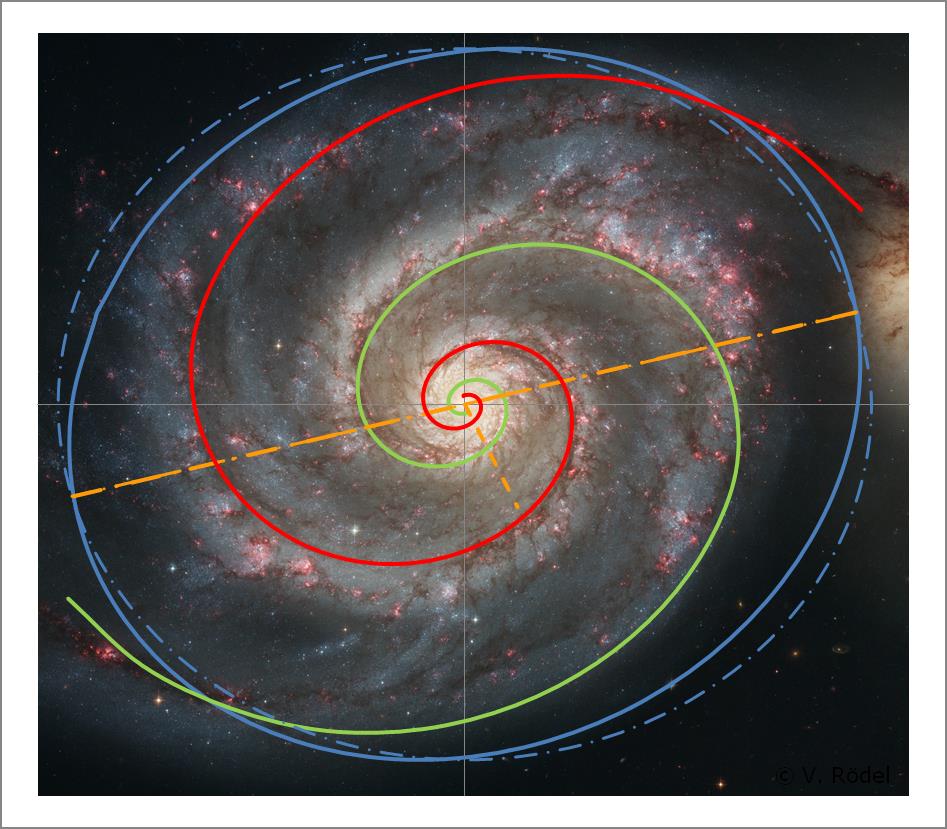
Abb. 11: Um die y-Achse gedrehte Spiralarme.

Durch die Schritte 1 bis 4 lässt sich auf diese Weise eine willkürlich im Raum angeordnete Galaxie, die aus irgendeinem Winkel fotografiert wurde, in die Ebene klappen. Die lotrechte Ansicht (Abb. 8) entspricht dann dem tatsächlichen Kurven­verlauf der Spiralarme.

Anschließend greifen wir einen dieser Spiral­arme heraus und können diesen mit seinen Energie­feldern betrachten. Auch hier geben die imaginären Grenz­linien der einzelnen Potentiale Rück­schlüsse auf die Rotations­energie.

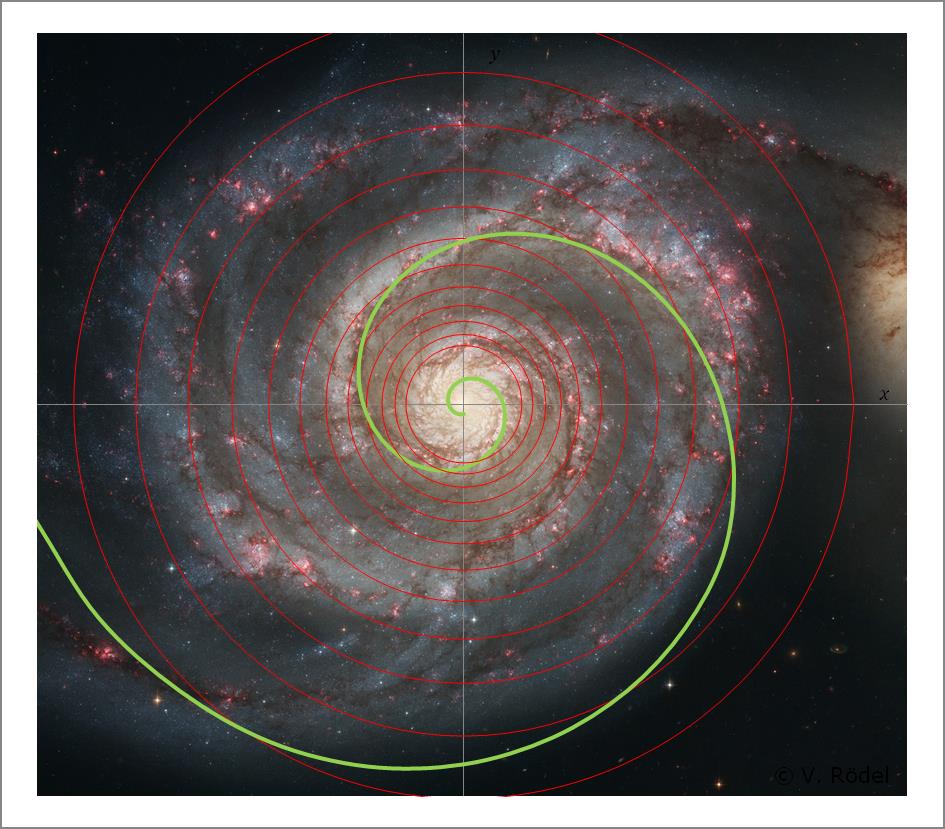
Abb. 12: Die Energiefelder in einer Galaxie.

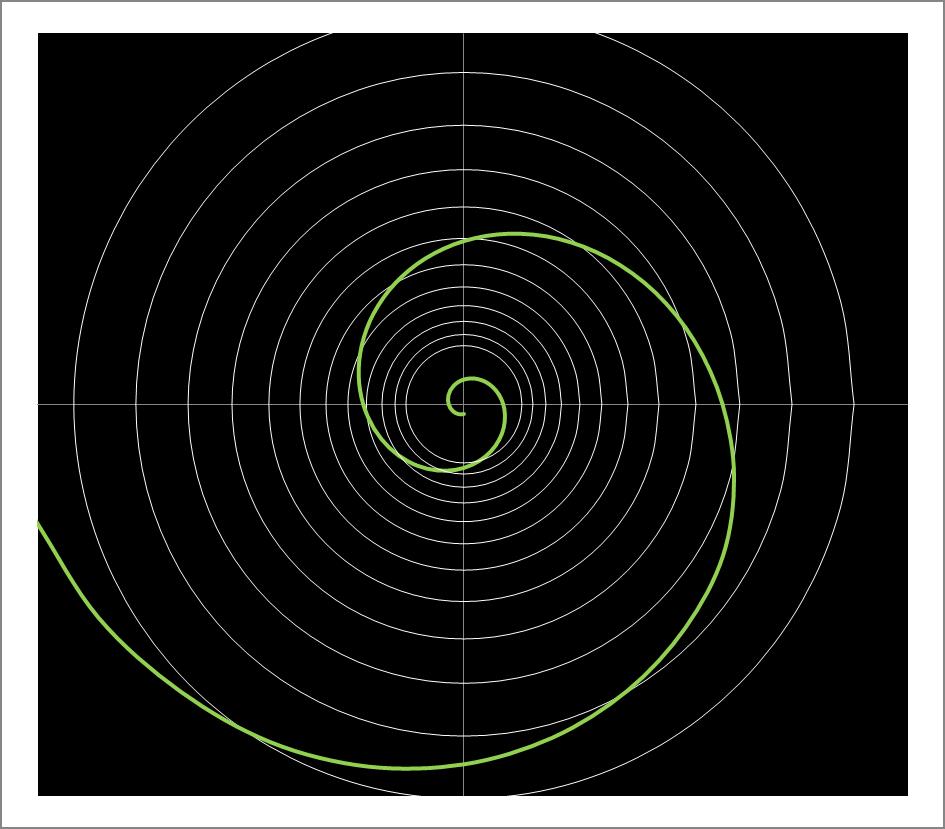
Abb. 13: Der Drehimpuls innerhalb des Potentialtrichters.

Die Spiralkurven auf dem Blütenkorb einer Sonnen­blume sind nichts anderes, wie die Spiral­kurven in einer Galaxie. Als Grund­lage dient immer die Logarithmische Spirale, wobei die Steigung k und damit die Krümmung der Bahn­kurven in den jeweiligen Systemen unter­schiedlich ist. Das hat im Wesentlichen damit zu tun, ob es sich um statische oder dynamische Strukturen handelt.

Abb. 14: Spiralmuster bei der Sonnenblume.

Die Polar­darstellung der Logarith­mischen Spirale ist definiert als:

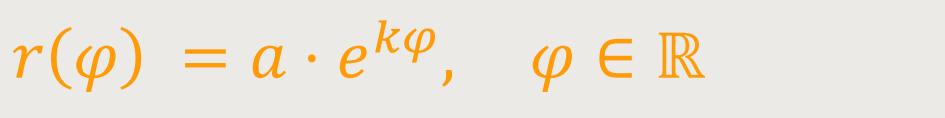
k   ist die Steigung der Spirale

Die Spirale lässt sich in karte­sischen Koordinaten (x = r · cos φ,   y = r · sin φ) durch die Parameter­darstellung beschreiben:

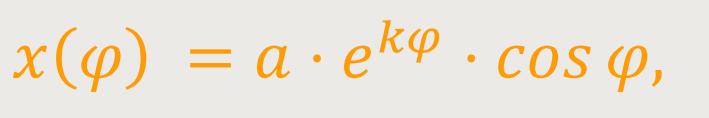
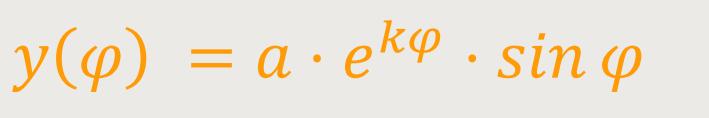
Die Spirale umkreist den Ursprung unendlich oft, ohne ihn zu erreichen.

Wir beschreiben die Polar­darstellung der Logarith­mischen Spirale jetzt mithilfe der Natur­konstanten Φ und π:

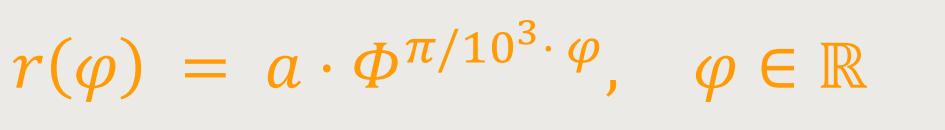
π/10³   ist die Steigung der Spirale

Die Spirale lässt sich in karte­sischen Koordinaten (x = r · cos φ,   y = r · sin φ) durch die Parameter­darstellung beschreiben:

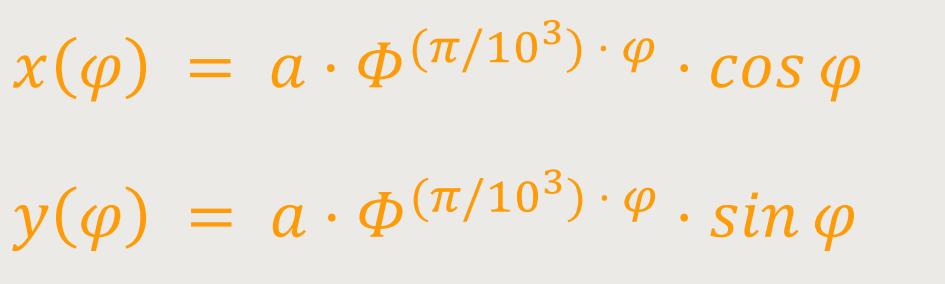
Da die Steigung jetzt die Natur­konstante π beinhaltet, ergibt sich ein Zusammen­hang zum 4-dimensionalen gekrümmten Raum. Ist die Steigung k nämlich > π, führt dies zu einer Expansion des Raums. Ist die Steigung k dagegen < π, führt dies zu einer Kontraktion des Raums.

Wenn sich ein System, wie zum Beispiel eine Galaxie um seinen Massen­schwerpunkt dreht, spricht man von einem Dreh­impuls. Der Dreh­impuls ist eine vektorielle Größe, und wie das Dreh­moment und die Winkel­geschwindigkeit ein sogenannter „Pseudovektor”. Das heißt, diese vektorielle Größe, behält bei einer Punkt­spiegelung des betrachteten physikalischen Systems ihre Richtung bei. Die Bahn­kurve, die sich aus dem Verlauf der Spiral­arme ergibt, beschreibt die unter­schiedlichen Rotations­geschwindigkeiten innerhalb des Systems. Der Gesamt­drehimpuls kann somit in Einzel­drehimpulse aufgeteilt werden.

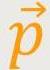Der Drehimpuls eines Massen­punktes lässt sich als Vektor­produkt aus dem Orts­vektor und dem Impuls des Massenpunkts berechnen:

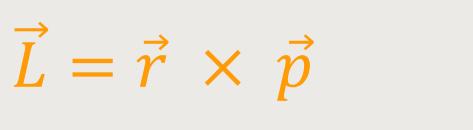
Wenn die nach innen gerichtete Kraft größer ist, als die an die Bahn­kurve angreifende Tangential­kraft, werden die Masse­teilchen nicht nur in Richtung des Zentrums gezogen, sondern sie beginnen ihrer­seits ebenfalls zu rotieren. So erhalten wir zwangs­läufig kleine Wirbel in einem großen Wirbel. Diese kleineren Wirbel können durchaus gegen­läufig sein. Ähnlich wie bei einem Zahnrad­getriebe, welches in einer Richtung aus immer kleiner werdenden Zahn­rädern besteht, wird sich die Umfangs­geschwindigkeit der Zahnräder entsprechend erhöhen.

Im Allgemeinen ist davon auszugehen, dass die Steigung der Bahn­kurven im Wesentlichen konstant bleibt. Es kann aber durchaus sein, dass sich der Radius während der Rotation ständig ändert, wie z. B. bei einer Bahn­ellipse oder einer anders gearteten Bahnkurve.

Die Bahnkurve der Spiral­arme verläuft grund­sätzlich durch zahlreiche imaginäre Grenz­linien. Je enger diese Grenz­linien beieinander­liegen, desto energie­reicher ist das Potential und desto größer ist die Geschwindigkeit der Masse­teilchen in dem Potential­trichter.

Das Wachstum eines Schnecken­hauses oder eines Blüten­korbes, wie bei der Sonnen­blume, läuft verhältnis­mäßig langsam ab. Was in dem einen Fall wenige Jahre dauert, beträgt im anderen Fall nur ein paar Monate. Je langsamer das Wachstum erfolgt, desto mehr nähert sich die Bahn­kurve der Logarithmischen Spirale an. Diese Spirale bildet eine der Grenz­linien in unserem Geschwindigkeits­schaubild ab.

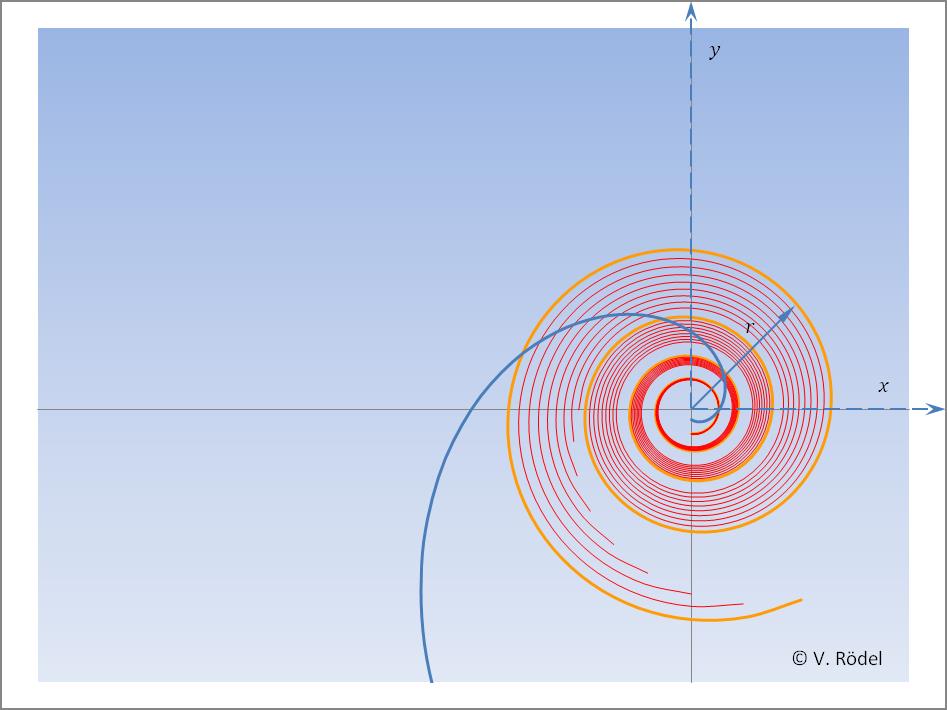
Abb. 15: Steigung der Geschwindigkeit ≤ π/10³.

Alles, was unterhalb dieser Grenz­linie liegt, lässt sich in den Bereich der Schwachen Kraft (Schwache Wechsel­wirkung) einordnen.

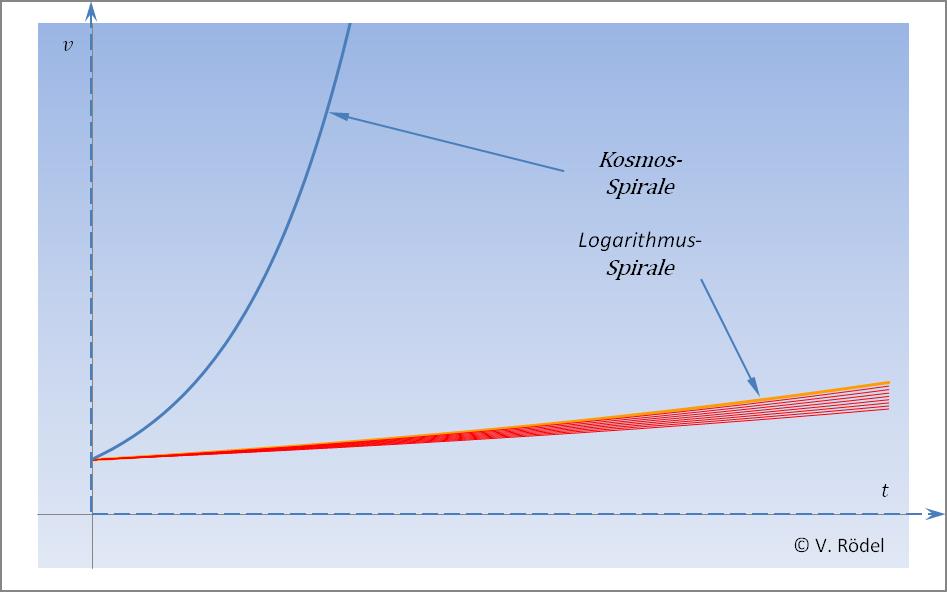
Abb. 16: Steigung der Geschwindigkeit ≤ π/10³.

Der überwiegende Bereich des Lebens spielt sich in der Region ab, dessen Steigung der Geschwindigkeiten zwischen der Logarithmischen Spirale und der Kosmos-Spirale liegt. Denn jede Struktur, egal ob Sonnen­blume, Sonnen­system oder Galaxie erreicht immer nur eine maximal mögliche Größe.

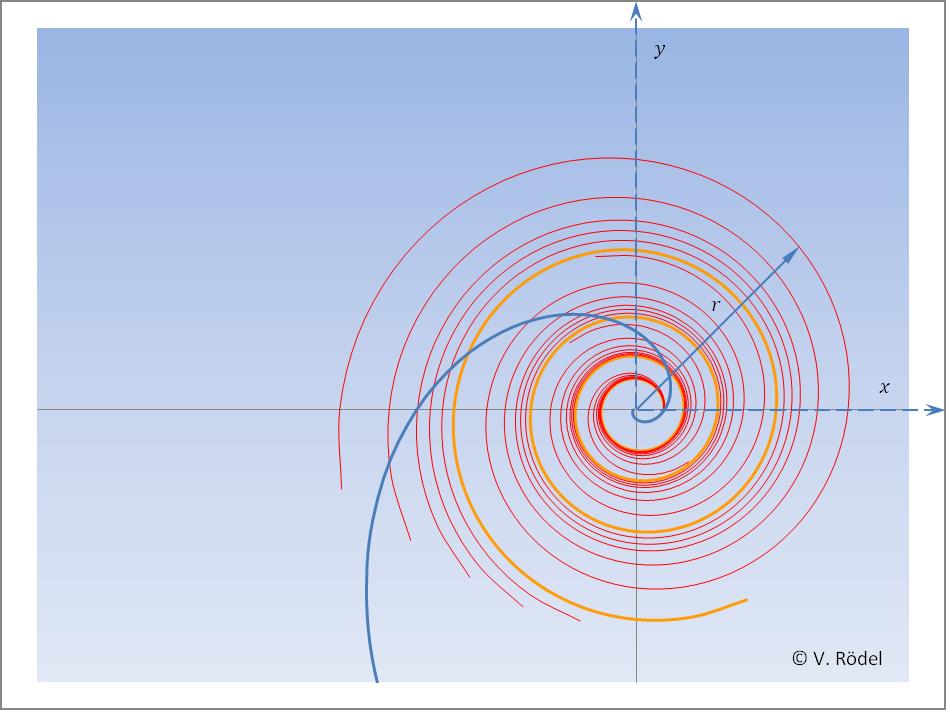
Abb. 17: Steigung der Geschwindigkeit ≥ π/10³ und ≤ Kosmos-Spirale.

Alles, was zwischen diesen beiden Grenz­linien liegt, lässt sich in den Bereich der Elektro­magnetischen Kraft (Elektro­magnetische Wechsel­wirkung) einordnen.

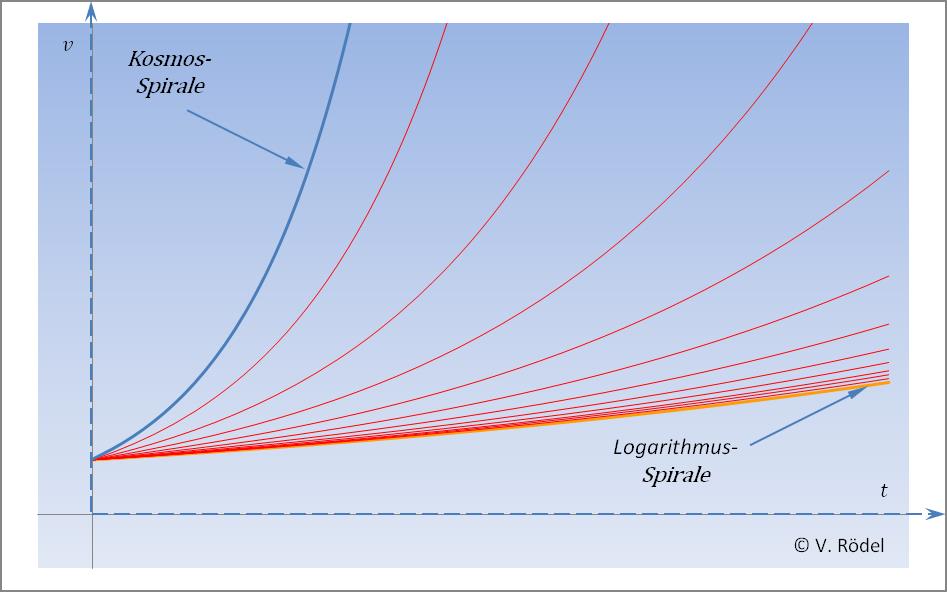
Abb. 18: Steigung der Geschwindigkeit ≥ π/10³ und ≤ Kosmos-Spirale.

Alles, was außerhalb des „stabilen” Bereichs liegt, neigt dazu auseinander zu driften, und wird von anderen benachbarten Strukturen einverleibt. Das ist zum Beispiel dann der Fall, wenn sich zwei Galaxien sehr nahe kommen und sich durch die Krümmung des Raums die Spiral­arme an den Rand­zonen aufgefächert werden. Dadurch verändert sich die Steigung und Krümmung der Bahn­kurve, sodass die Energie nicht mehr dem Gesamtdreh­impuls des Systems unter­liegt und dem­entsprechend nach außen abgegeben wird.

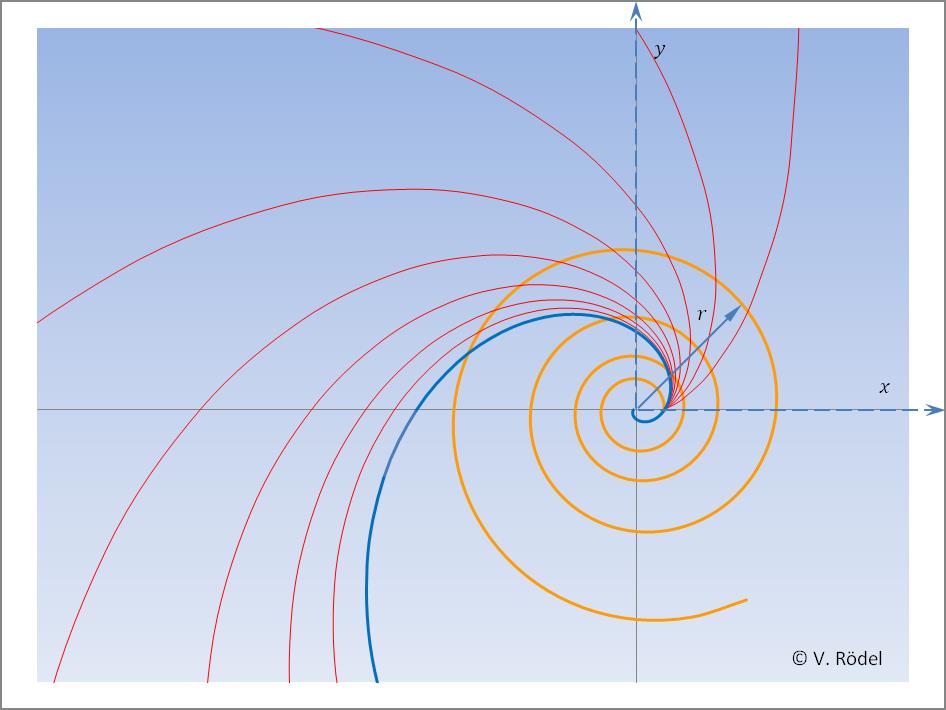
Abb. 19: Steigung der Geschwindigkeit ≥ Kosmos-Spirale.

Alles, was oberhalb der oberen Grenz­linie liegt, lässt sich in den Bereich der Starken Kraft (Starke Wechsel­wirkung) einordnen.

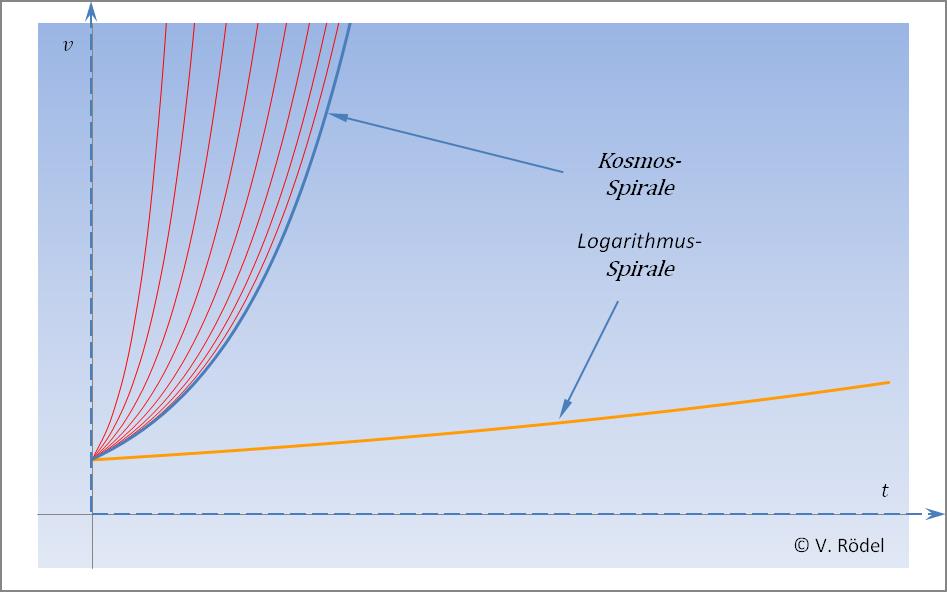
Abb. 20: Steigung der Geschwindigkeit ≥ Kosmos-Spirale.

Der Drehimpuls der Whirlpool-Galaxie lässt sich ohne Weiteres in eines dieser Schau­bilder über­tragen. Wie nicht anders zu erwarten, tendiert die Steigung der Geschwindigkeit in die Nähe der Kosmos-Spirale.

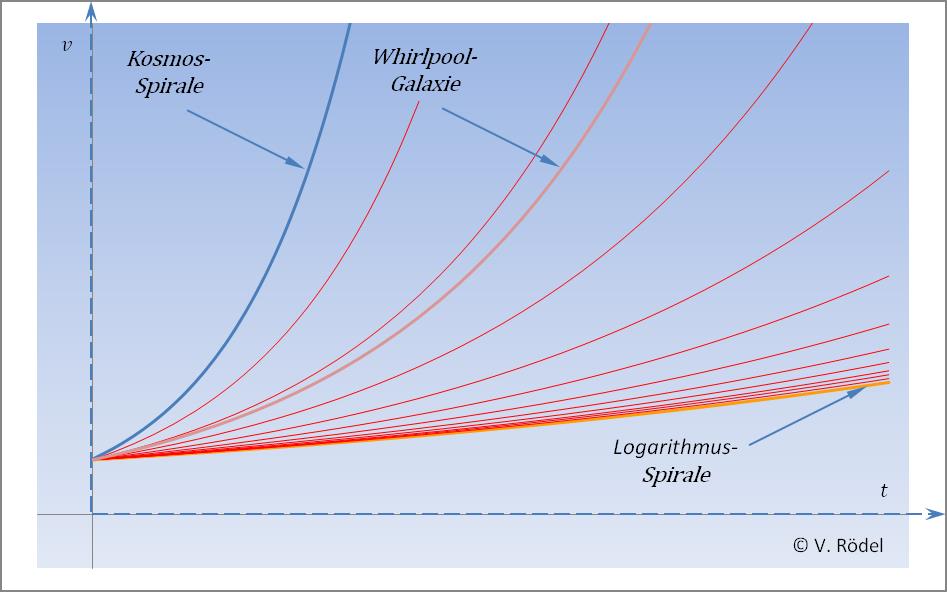
Abb. 21: Die Steigung der Geschwindigkeit der Whirlpool-Galaxie liegt im Bereich > π/10³, und tendiert Richtung Kosmos-Spirale.

Bevor wir die Wirbel­strukturen in einer Galaxie noch genauer betrachten, möchten wir uns noch kurz ein Phänomen bei der Entstehung von Wirbeln anschauen.

Bei der oberflächlichen Betrachtung eines Wirbels könnte man davon ausgehen, dass die kleineren Wirbel im Innern alle in die gleiche Richtung rotieren. Experimente fördern jedoch Erstaunliches zutage.^[1]

Zwei ineinander verschachtelte Wirbel können einen dritten Wirbel erzeugen, der sich in entgegen­gesetzter Richtung dreht. Das wider­spricht der allgemeinen Auffassung, dass die Anzahl der Wirbel in einem turbulenten System mit der Zeit abnimmt. Man kann das Wirbel­verhalten einer perfekten Flüssigkeit mittels einer Apparatur simulieren, die Elektronen in einem Magnetfeld gefangen hält.

Die mathe­matischen Gleichungen, die das Verhalten von Elektronen in einem Magnet­feld beschreiben, sind mit denen von Wirbeln in einer perfekten Flüssigkeit identisch. Dabei entspricht die Elektronen­dichte der Stärke des Wirbels. In realen Flüssig­keiten wird das Verhalten der Wirbel allerdings durch Reibungs­kräfte gestört.

Erzeugt man einen kleinen starken Wirbel innerhalb eines größeren schwächeren Wirbels, wobei sich beide in die gleiche Richtung drehen, wie das zum Beispiel auch in Galaxien oder Sonnen­systemen der Fall ist, lässt sich beobachten, dass der kleine Wirbel ein wellen­artiges Kräuseln auf dem Rand des äußeren Wirbels erzeugt. Dieses Kräuseln pflanzt sich auf dem Rand fort, wobei es sich vergrößert und sich schließlich selbst einholt.

Dabei entsteht ein „Wirbelloch”, welches sich wie ein umgekehrt drehender Wirbel verhält. Dieses Wirbel­loch ermöglicht es dem kleinen Wirbel, Energie mit dem großen Wirbel auszutauschen. Im weiteren Verlauf zieht der kleine Wirbel dieses Wirbelloch weiter in das Innere des großen Wirbels. Dabei geht das gesamte System in ein chaotisches Verhalten über.

Interessanterweise spielt dieses Phänomen bei der Entstehung von Tornados innerhalb von Hurrikans eine Rolle. Ähnliches kann man auch bei dem Roten Fleck auf der Oberfläche des Planeten Jupiter beobachten.

Der Materiefluss strömt innerhalb eines Wirbels rein kreis­förmig oder besser gesagt spiralförmig und zeit­abhängig sowie instationär um das Wirbel­zentrum. Die Visko­sität zehrt die kinetische Energie des Wirbels mit der Zeit auf und die Strö­mungs­geschwin­dig­keit nimmt monoton mit der Zeit ab.

Allerdings verhält es sich in einem hyper­bolischen Strömungs­fluss etwas anders. Dort nimmt die Geschwindigkeit zu, weil sich die Materie­teilchen den zunehmenden Scher­kräften widersetzen.

Doch im Allgemeinen, zu Beginn der Bewegung oder im Grenz­fall verschwin­dender Visko­sität, ist der Wirbel ein Potential­wirbel. Ansonsten ist das Geschwin­dig­keits­profil des Hamel-Oseenschen-Wirbels beschränkt und ent­spricht im Wirbel­kern, sowie im Außen­bereich einem Rankine-Wirbel.

Auch wenn man es nicht für möglich hält, aber der Materiefluss lässt sich sehr schön an einem Blütenkorb einer Sonnen­blume nach­vollziehen. Das beeindruckende Spiral­muster einer Sonnen­blume, lässt sich ohne Weiteres auch auf eine Galaxie über­tragen.

Abb. 22: Das Spiralmuster einer Sonnenblume.

Obwohl die Sonnen­blume als 3-dimensionale Struktur doch einen relativ flachen Blüten­korb abbildet, kann man an dieser Grafik sehr schön den hyper­bolischen Charakter erahnen. Die Drauf­sicht dieser Grafik gibt jedoch keine Rück­schlüsse darüber, wie gekrümmt die Ober­fläche der jeweiligen Struktur in der Realität ist.

In einer bestimmten Lebens­phase aller­dings wird eine solche Struktur immer flacher, egal ob es sich dabei um einen Blüten­korb, die Ekliptik eines Sonnen­systems oder die eine Galaxie handelt. Die ursprüngliche Kugel­form, oder besser gesagt das Ellipsoid, wird sich aufgrund der Rotation und der damit verbundenen Flieh­kräfte topologisch immer mehr zu einer räumlich flachen Scheibe ausbilden.

Abb. 23: Die linksläufigen und rechtsläufigen Wirbel, wie sie auch in einer Galaxie zu finden sind.

Gegenläufige Wirbel sind nicht nur charakteristisch für ein Fluid, egal ob es sich dabei um Wasser oder ein Medium aus Gas handelt. Auch der Materie­fluss in einer Galaxie zeichnet sich durch ineinander verschachtelte Wirbel­strukturen aus, die sich kaskadisch fort­pflanzen.

Dass sich diese Wirbel­strukturen in einer realen Galaxie nicht so einfach nach­vollziehen lassen, hängt mit den unter­schiedlichen anfänglichen Dichte­verteilungen in einer Akkretions­scheibe zusammen. Obige Grafik zeigt die Wirbel­strukturen in einem homogenen Medium. Was hier flach dargestellt ist, sind in Wirklichkeit alles Ellipsoide, die kaskadisch angeordnet sind, und in das Zentrum eines rotierenden Systems hineinspiralen.

Vergrößert man den unteren, rechten Bereich, kann man sehr schön die wechsel­seitig angeordneten und gegen­läufigen Wirbel erkennen, die sich auf diese Weise bis auf Molekül­größe in dem Medium fortpflanzen.

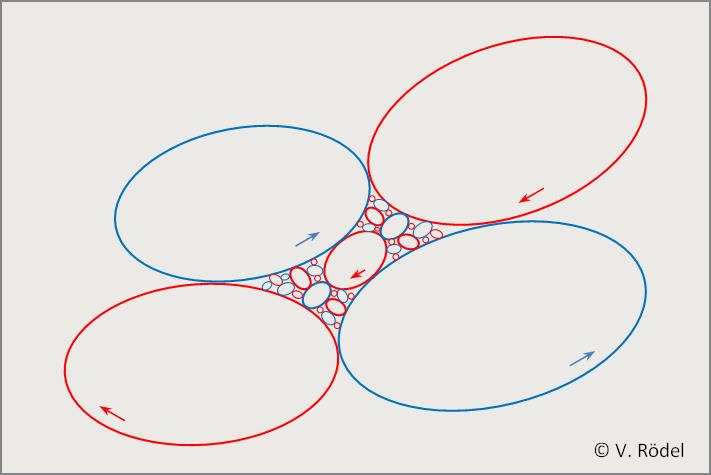
Abb. 23: Die linksläufigen und rechtsläufigen Wirbel in den Zwischenbereichen.

Innerhalb der Potentialfelder manifestieren sich schließlich die Wirbel zu Akkretions­scheiben und später zu Galaxien und zwar dort, wo die Wirbel die größte Energie haben. Die gesamte Materie innerhalb des Potentials wird quasi aufgesogen und zu einer Proto­galaxie geformt.

Und während die Materie ins Zentrum spiralt, lässt sich eine Drift bei den Molekülen beobachten.

Abb. 24: Die Drift des Materieflusses.

Wie das im Detail aussieht, und wie sich daraus der Dreh­impuls einer Galaxie ableiten lässt, wird in einem zukünftigen Kapitel näher betrachtet.

Eine weitere beeindruckende Galaxie ist unsere Nachbar­galaxie, der Andromeda-Nebel, von der wir sehr viel über unsere Heimat­galaxie abzuleiten versuchen. Auch dazu künftig mehr.

Abb. 23: Andromeda Galaxie (© NASA/JPL-Caltech)

Quellen

[1] Versuchsaufbau von Dan Durkin und Joel Fajans von der Universität von Kalifornien in Berkeley

⇦ Kapitel Kapitel ⇨