Wer sich mit der Relativitäts­theorie befasst, muss sich zunächst darüber im Klaren sein, um welche Variante dieser Theorie es geht.

Albert Einstein hatte zuerst im Jahr 1905 die Spezielle Relativitäts­theorie ent­wickelt, die im Wesent­lichen das Ver­halten von Raum und Zeit aus der Sicht von Beobach­tern beschreibt, die sich relativ zueinander bewegen, und die damit ver­bundenen Phänomene.

Seine zweite allge­meinere Fassung, die er am 25. November 1915 der Preu­ßischen Akademie der Wissen­schaften vortrug und die schließlich im Jahr 1916 publiziert wurde, ist mehr unter der Allge­meinen Relativitäts­theorie bekannt. Darin geht es im Wesent­lichen um die Gravi­tation, die auf eine Krüm­mung von Raum und Zeit zurück­geführt wird, und die unter anderem durch die beteiligten Massen verursacht wird.

Als Einstieg sollte man auch ver­stehen, was es mit dem Begriff Relativität auf sich hat. Es hat nichts mit dem Adjektiv „relativ” zu tun, in dem Sinne, dass es nur auf den Betrach­tungs­winkel ankommt. Viel­mehr geht es dabei um die Geschwin­dig­keit von Systemen. Genauer gesagt um die Relativ­geschwin­dig­keit zweier Systeme zueinander.

Einstein würdigte den Beitrag des Mathe­matikers Minkowski, der als erstes die formale Gleich­wertig­keit der räum­lichen Koordinaten und der Zeit­koordinate erkannte und die Einstein für den Aufbau seiner Theorie nutzte. Die für die Allgemeine Relativi­täts­theorie not­wendigen Hilfs­mittel lagen aus Einsteins Sicht alle bereit, und mussten nur noch zusammen­geführt werden.

Ein großes Thema sollte hierbei die Differential­geometrie spielen, mit der Einstein bestens vertraut war, und die auf den Forschungen von Gauss, Riemann, und Christoffel über nicht­euklidische Mannig­faltig­keiten beruht. Und schließ­lich von Ricci und Levi-Civita in einen Forma­lismus gebracht wurde. Diese hatten sich in der theore­tischen Physik bereits bestens bewährt.

Unter einer Mannig­faltig­keit versteht man in der Mathe­matik einen topolo­gischen Raum, der lokal dem eukli­dischen Raum Rⁿ gleicht. Global muss die Mannig­faltig­keit jedoch nicht einem eukli­dischen Raum gleichen. Der eukli­dische Raum ist zunächst der „Raum unserer Anschauung”. Der Zusatz „euklidisch” wurde nötig, nachdem in der Mathe­matik all­gemeinere Raum­konzepte entwickelt wurden. Dazu gehören zum Beispiel der hyper­bolische Raum und die Riemannschen Mannig­faltig­keiten. Im Rahmen der Speziellen und Allgemeinen Relativitätstheorie zeigte sich, dass zur Beschreibung des Raumes in der Physik andere Raum­begriffe benötigt werden.

Einstein unter­teilte seine Abhand­lung in zwei Abschnitte und diese wiederum in 5 Bereiche. Im ersten Abschnitt geht es um prinzi­pielle Erwägungen zum Postulat der Speziellen Relativi­täts­theorie.

Im zweiten Abschnitt geht es darum, die ange­sprochenen mathe­matischen Hilfs­mittel insbe­sondere für unkundige Physiker in möglichst einfacher und nach­voll­zieh­barer Weise zu ent­wickeln, sodass ein Mathematik­studium keine Voraus­setzung darstellt. In diesem Zusammen­hang dankte Einstein seinem Freund Grossmann, der als Mathe­matiker ihm mit Rat und Tat zur Seite stand, und Einstein so ein Studium der einschlä­gigen mathe­matischen Literatur ersparte. Grossmann unter­stütze ihn auch bei der richtigen Auswahl der Feld­gleichungen bezüg­lich der Gravitation.

§ 1. Bemerkungen zur Speziellen Relativitätstheorie

Einsteins Hinweis entspre­chend stützt sich die Spezielle Relativitätstheorie auf die Gesetzte der Mechanik, basierend auf Galilei und Newton. Wird ein Koordi­naten­system K gewählt, in welchem die physika­lischen Gesetze gelten, so gelten auch in einem anderen Koordi­naten­system K' dieselben Gesetze, wenn sich dieses beispiels­weise relativ zu K in gleich­förmiger Trans­lations­bewegung befindet. Dieses Prinzip nannte Einstein „Spezielles Relativitätsprinzip”. Das Wort speziell deutet an, dass es sich hierbei um einen Spezial­fall handelt, nämlich das K' eine gleich­förmige Translations­bewegung gegenüber K ausführt. Die Gleich­wertig­keit von K' und K gilt jedoch nicht für den Fall ungleich­förmiger Bewegung beider Systeme zueinander.

Die Spezielle Relativi­täts­theorie weicht nur in einem Punkt von der klassischen Mechanik ab, und zwar was die Konstanz der Vakuum-Licht­geschwin­dig­keit angeht. Aus dem speziellen Relativi­täts­prinzip folgt die Relativität der Gleich­zeitig­keit sowie der Lorentz­transformation. Das wiederum hat nach Einsteins Worten Einfluss auf das Verhalten bewegter starrer Körper und Uhren.

Die Spezielle Relativi­täts­theorie ist zwar durch die Theorie von Raum und Zeit erweitert worden, aber trotz­dem gelten weiter­hin die Grund­lagen der Geometrie, insbe­sondere die Gesetze der Kinematik, die beispiels­weise auch das Ver­halten von Mess­körpern und Uhren beschrei­ben. Mit anderen Worten, zwei Bezugs­punkte eines ruhenden starren Körpers ent­sprechen stets einer ganz bestimmten Länge unabhängig vom Ort und der Lage sowie der Zeit. Oder zwei fest­gehal­tenen Zeiger­stellungen einer relativ zu einem bevor­zugten Bezugs­system ruhenden Uhr ent­spricht stets eine Zeit­strecke von bestimmter Länge, unab­hängig von Ort und Zeit.

Nach Einsteins Worten wird die Allgemeine Relativi­täts­theorie an dieser ein­fachen physika­lischen Beschreibung von Raum und Zeit nicht fest­halten können.

§ 2. Gründe, die eine Erweiterung des Relativitätspostulats nahelegen

Einstein war davon über­zeugt, dass in der klassischen Mechanik und selbst der Speziellen Relativi­täts­theorie eine tiefer­gehende theore­tische Erkenntnis fehlte, auf die seiner­zeit bereits Ernst Mach aufmerksam gemacht hatte. Einstein versuchte das Problem an folgendem Beispiel zu erläutern:

Man denke sich zwei flüssige Körper von gleicher Größe und Struktur, die frei im Raum schweben. Beide Körper seien so weit voneinander und von anderen Massen entfernt, dass nur die Gravi­tations­kräfte berück­sichtigt werden müssen, die eines dieser Körper auf den anderen ausübt. Die Ent­fernung beider Körper zueinander soll sich nicht ändern. Und es soll auch keinen gegen­seitigen Einfluss der Körper geben, wie zum Beispiel durch relative Bewegungen. Außerdem sitzt auf jeder der beiden Massen ein Beobachter, der aus Sicht seines ruhenden Systems die andere Masse beobachtet.

Des Weiteren soll jede Masse um eine gedachte Verbindungs­linie beider Massen mit konstanter Winkel­geschwin­dig­keit rotieren. Es lässt sich vorher­sagen, dass es zu einer Relativ­bewegung beider Massen kommen wird. Wäre man nun in der Lage, die Ober­flächen beider Körper S₁ und S₂ mit einem relativ zum Körper ruhenden Maßstab zu messen, würde sich folgendes ergeben: Die Ober­fläche des Ruhe­systems S₁ würde einer Kugel entsprechen, wogegen das System S₂ am anderen Ende der gedachten Verbindungs­linie ein Rotations­ellipsoid sei.

Nun erhebt sich die Frage, warum verhalten sich die Körper S₁ und S₂ aus Sicht des jeweiligen Betrachters verschieden? Die Antwort kann nach Einsteins Worten aus Sicht der theore­tischen Erkenntnis nur dann zufrieden­stellend sein, wenn die Ursache durch beobacht­bare Erfah­rungen bestätigt wird. Denn die Ursäch­lich­keit kann nur dann als Aussage über das Gesetz von Ursache und Wirkung heran­gezogen werden, wenn es mit der Realität über­einstimmt.

Laut Einstein gibt die Newtonsche Mechanik auf diese Frage keine befrie­digende Antwort. Newtons Mechanik würde nämlich folgendes aussagen:

Die Gesetze der Mechanik gelten zwar für einen Raum R₁ in welchem der Köper S₁ in Ruhe verharrt, nicht aber für einen Raum R₂, in welchem ein Körper S₂ in Ruhe ist. Der maß­gebliche Galileische Raum, in welchem alle Inertial­systeme gleich­berechtigt sind, und in denen die gleichen physika­lischen Gesetze gelten, kann bloß als vermutete Ursache heran­gezogen werden, da sie nach Einsteins Worten nicht beobacht­bar sei. Daraus ergäbe sich die Schluss­folgerung, dass die Newtonsche Mechanik der Forderung nach einem Zusammen­hang in obigem Fall nur schein­bar Genüge leistet, indem sie die vermutete Ursache, nämlich den Raum R₁ für das unter­schied­liche Ver­halten der Körper S₁ und S₂ ver­antwort­lich macht.

Für Einstein lässt die oben aufgeworfene Frage nur eine befriedigende Antwort zu: Das aus S₁ und S₂ bestehende physika­lische System zeigt für sich allein keine nachvollbare Ursache, auf die das unter­schied­liche Ver­halten von S₁ und S₂ zurück­geführt werden könne. Die Ursache muss nach seiner Auf­fassung außer­halb dieses Systems liegen. Man gelangt zwangs­läufig zu der Auf­fassung, dass die gültigen Bewegungs­gesetze, welche die Form­gebung von S₁ und S₂ bestimmen, darin begründet liegen, dass das mechanische Verhalten von S₁ und S₂ durch ferne Massen mit beeinflusst wird, die aber bisher über­sehen wurden. Diese fernen Massen und deren Relativ­bewegungen zu den betrach­teten Körpern sind als Über­mittler der Ursachen anzusehen. Sie über­nehmen dann die Rolle der vermuteten Ursache im Raum R₁.

Einstein war davon über­zeugt, dass von allen denk­baren, relativ zueinander beliebig bewegten Räumen R₁, R₂ usw. darf von vorn­herein keiner als bevor­zugt angesehen werden, wenn nicht der dargelegte Einwand nach dem theore­tischen Verstän­dnis wieder aufleben soll. Die Gesetze der Physik müssen so beschaffen sein, dass sie in Bezug auf beliebig bewegte Bezugs­systeme gelten. Auf diesem Wege würde man nach seinen Worten zu einer Erweiterung des Relativi­täts­postulats gelangen.

Außer diesem schwer­wiegenden Argument spricht auch eine wohl­bekannte physika­lische Tatsache für eine Erwei­terung der Relativi­täts­theorie. Es sei K ein Galileisches Bezugs­system, das heißt ein solches, zu dem sich relativ (mindestens in dem betrachteten 4-dimen­sionalen Bereich) eine von anderen aus­reichend ent­fernte Masse gerad­linig und gleich­förmig bewegt. Es sei ferner K' ein zweites Koordinaten­system, welches relativ zu K in gleich­förmig beschleu­nigter Translations­bewegung sei. Relativ zu K' soll dann eine von anderen aus­reichend getrennte Masse eine beschleu­nigte Bewegung aus­führen, und zwar so, dass deren Beschleu­nigung und Beschleu­nigungs­richtung von ihrer stoff­lichen Zusammen­setzung und ihrem physika­lischen Zustand unabhängig ist.

An dieser Stelle wirft Einstein die Frage auf, ob ein relativ zu K' ruhender Beobachter hieraus den Schluss ziehen kann, dass er sich auf einem „wirklich” beschleu­nigten Bezugs­system befindet? Diese Frage sei zu verneinen.

Denn das zuvor genannte Ver­halten frei beweglicher Massen relativ zu K' könne ebenso gut auf folgende Wiese gedeutet werden: Das Bezugs­system K' ist unbeschleu­nigt. Dann würde in dem betrachteten raum­zeit­lichen Gebiet ein Gravita­tions­feld herrschen, welches die beschleu­nigte Bewegung der Körper relativ zu K' erzeugt.

Diese Auffassung würde dadurch unter­mauert, dass uns die Erfahrung das Vorhanden­sein eines Kraft­feldes, nämlich des Gravi­tations­feldes, gelehrt hätte, welches die merk­würdige Eigen­schaft hat, auf alle Körper dieselbe Beschleu­nigungs­kraft auszu­üben. Als Beweis führt Einstein das Experiment von Loránd Eötvös an, der das präzise Ver­halten des Gravita­tions­feldes bestätigt hat.

Das mechanische Ver­halten der Körper relativ zu K' sei dasselbe, wie es bei Systemen zu beobachten ist, die wir gewohnheits­mäßig als ruhendes bzw. bevor­zugtes System ansehen würden. Deshalb liegt es auch vom physika­lischen Stand­punkt aus nahe, anzu­nehmen, dass die Systeme K und K' gleich­berechtigt als ruhend angesehen werden können. Oder dass sie als Bezugs­systeme für die physika­lische Beschrei­bung der Vorgänge als gleich­berechtigt gelten.

Aus diesen Über­legungen zog Einstein den Schluss, dass die Abhandlung der Allgemeinen Relativitätstheorie zugleich zu einer Theorie der Gravi­tation führen muss. Denn man könne ein Gravi­tations­feld durch bloße Änderung des Koordi­naten­systems „erzeugen”. Ebenso würde man unmittel­bar erkennen, dass das Prinzip von der Konstanz der Vakuum-Licht­geschwin­dig­keit modi­fiziert werden müsse. Denn man sieht sofort, dass die Bahn eines Licht­strahls in Bezug auf K' im All­gemeinen gekrümmt sein müsse, wenn sich das Licht in Bezug auf K gerad­linig und mit bestimmter, konstanter Geschwin­dig­keit fort­pflanzt.

§ 3. Das Raum-Zeit-Kontinuum. Forderung der allgemeinen Kovarianz für die die allgemeinen Naturgesetze ausdrückenden Gleichungen.

In der klassischen Mechanik sowie in der Speziellen Relativi­täts­theorie haben die Koordi­naten des Raumes und der Zeit eine unmittel­bare physika­lische Bedeu­tung. Ein Punkt­ereignis hat die X₁-Koordi­nate x₁, was bedeutet: Die nach den Regeln der Eukli­dischen Geometrie mittels starrer Stäbe ermittelte Projektion des Punkt­ereig­nisses auf die X₁-Achse erhält man, indem man einen bestimmten Stab, den Einheits­maßstab, x₁-mal vom Anfangs­punkt des Koordi­naten­körpers auf der positiven X₁-Achse abträgt. Ein Punkt hat die X₄-Koordi­nate x₄ = t, was bedeutet: Eine relativ zum Koordi­naten­system ruhend ange­ordnete, und mit dem Punkt­ereignis räum­lich zusammen­fallende Einheits­uhr, welche bestimmte Vor­schriften erfüllt, hat beim Eintreten des Punkt­ereignisses x₄ = t Perioden zurück­gelegt.

Nach Aussage Einsteins schwebte diese Auf­fassung von Raum und Zeit den Physikern stets vor, wenn auch meist unbewusst. Dies sei klar erkennbar, wenn man bedenkt, welche Rolle diese Begriffe in der messenden Physik spielen. Um diese Aus­füh­rungen sinn­voll nach­voll­ziehen zu können, müsste man beim Lesen des voran­gegangen eine ähnliche Auf­fassung haben. Aller­dings wollte Einstein nun zeigen, dass man diese Auf­fassung fallen lassen und durch eine All­gemeinere ersetzen muss, um das Postulat der all­gemeinen Relativi­tät durch­führen zu können. Natür­lich gesetzt dem Fall, dass die Spezielle Relativi­täts­theorie für den Grenz­fall des Fehlens eines Gravi­tations­feldes zutrifft.

Zur weiteren Argumentation führt Einstein jetzt einem Raum ein, und zwar ein Galileisches Bezugs­system K (x, y, z, t), der frei sein soll von jeglichen Gravi­tations­feldern, und außer­dem ein relativ zu K gleich­förmig rotierendes Koordinaten­system K' (x', y', z', t'). Die Anfangs­punkte beider Systeme sowie deren z-Achsen mögen stets zusammen­fallen. Einstein wollte nun zeigen, dass für eine Raum-Zeit-Messung im System K' die obige Fest­legung für die physika­lische Bedeutung von Längen und Zeiten nicht aufrecht­erhalten werden kann. Aus Symmetrie­gründen sei klar, dass ein Kreis um den Anfangs­punkt in der X-Y-Ebene von K, zugleich als Kreis in der X'-Y'-Ebene von K' aufge­fasst werden kann. Der Umfang und Durch­messer dieses Kreises soll relativ zum Radius mit einem unendlich kleinen Einheits­maßstab ausge­messen werden. Anschlie­ßend wird der Quotient, also das Ver­hältnis, beider Mess­resultate gebildet. Würde man dieses Experiment mit einem relativ zum Galileischen System K ruhenden Maßstab aus­führen, so würde man als Quotienten die Zahl π erhalten. Das Resultat der mit einem relativ zu K' ruhenden Maßstab ausge­führten Fest­legung würde eine Zahl sein, die größer ist als π. Man würde dies leicht erkennen, wenn man den ganzen Mess­prozess vom „ruhenden” System K aus beurteilt und berück­sichtigt, dass der periodisch angelegte Maßstab eine Lorentz­verkür­zung voll­zieht, der radial ange­legte Maßstab aber nicht. Es gilt daher in Bezug auf K' nicht die Euklidische Geometrie.

Der oben festge­legte Koordinaten­begriff, welcher die Gültig­keit der Eukli­dischen Geometrie voraus­setzt, würde also mit Bezug auf das System K' versagen. Ebenso wenig könne man in diesem rotie­renden Koordinaten­system K' eine den physika­lischen Bedürf­nissen entspre­chende Zeit ein­führen, welche durch relativ zu K' ruhende, gleich geschaffene Uhren ange­zeigt wird. Um das nach­voll­ziehen zu können, denke man sich im Koordinaten­ursprung und an der Rand­zone des Kreises je eine von zwei gleich beschaffenen Uhren angeordnet, die vom „ruhenden” System K aus betrachtet werden. Nach dem bekannten Resultat der Speziellen Relativitätstheorie geht, von K aus beurteilt, die auf der Kreis­peripherie ange­ordnete Uhr langsamer als die im Koordi­naten­ursprung angeordnete Uhr, weil erstere bewegt ist, letztere aber nicht.

Ein im gemeinsamen Koordinaten­ursprung befindlicher Beobachter, der auch die an der Rand­zone befind­liche Uhr mittels des Lichtes zu beobachten in der Lage wäre, würde dement­sprechend die an der Rand­zone angeordnete Uhr lang­samer gehen sehen, als die neben ihm geordnete Uhr. Da er sich nicht dazu entschließen wird, die Licht­geschwin­dig­keit auf dem in Betracht kommenden Weg explizit von der Zeit abhängig zu machen, wird er seine Beobachtung so inter­pretieren, dass die Uhr an der Rand­zone „wirklich” lang­samer geht, als die im Ursprung ange­ordnete. Er wird also nicht umhin können, die Zeit so zu definieren, dass die Gang­geschwin­dig­keit einer Uhr vom Ort abhängt.

Laut Einstein gelangt man also zu folgendem Ergebnis: In der Allgemeinen Relativi­täts­theorie können Raum- und Zeit­größen nicht so definiert werden, dass räum­liche Koordinaten­differenzen unmittel­bar mit dem Einheits­maßstab, zeit­liche dagegen mit einer Normal­uhr gemessen werden könnten.

Die bisherige Vorgehens­weise, in das raum­zeit­liche Kontinuum in bestimmter Art und Weise Koordinaten zu legen, versagt also. Und es scheint sich auch kein anderer Weg anzu­bieten, der es möglich machen würde, in einer 4-dimen­sionalen Welt die Koordi­naten­systeme so anzu­passen, dass bei ihrer Ver­wendung, eine besonders einfache Formu­lierung der Natur­gesetze zu erwarten wäre. Es bliebe daher nichts anderes übrig, als alle denk­baren Koordi­naten­systeme prinzipiell für die Natur­beschrei­bung als gleich­berechtigt anzu­sehen. In diesem Fall ergibt sich folgende Forderung:

Die all­gemeinen Natur­gesetze sind durch Gleichungen auszu­drücken, die für alle Koordinaten­systeme gelten, das heißt die beliebigen Substi­tutionen gegen­über kovariant sind.

Nach Einsteins Auf­fassung ist klar, dass eine Physik, die diesem Postulat genügt, dem all­gemeinen Relativi­täts­postulat gerecht wird. Denn in „allen” Substitu­tionen seien jeden­falls auch die­jenigen ent­halten, welche allen Relativ­bewegungen der klassischen 3-dimen­sionalen Koordinaten­systeme ent­sprächen. Dass diese Forderung der all­gemeinen Kovarianz, die dem Raum und der Zeit den letzten Rest physika­lischer Gegen­ständ­lich­keit nimmt, eine natur­gegebene Voraus­setzung sei, würde aus folgender Über­legung hervor­gehen: Alle unsere raum­zeit­lichen Vorher­sagen laufen stets auf die Bestimmung raum­zeit­licher Koinzi­denzen hinaus. Würde beispiels­weise das Geschehen nur in der Bewegung materieller Punkte bestehen, so könnte man letzten Endes nicht mehr beobachten, als die Begegnungen zweier oder mehrerer dieser Punkte. Auch die Ergeb­nisse unserer Messungen sind nichts anderes als die Vorher­sage der­artiger Begeg­nungen materieller Punkte unserer Maßstäbe mit anderen materiellen Punkten bzw. den Koinzi­denzen zwischen Uhrzeigern, Zifferblatt­punkten und ins Auge gefassten, am gleichen Orte und zur gleichen Zeit statt­findenden Punkt­ereignissen.

Die Einführung eines Bezugs­systems dient daher zu nichts anderem als zur leichteren Beschrei­bung der Gesamt­heit solcher Koinzi­denzen. Man ordnet der Welt vier raum­zeit­liche Variable x₁, x₂, x₃, x₄ zu, in der Weise, dass jedem Punkt­ereignis ein Werte­system der Variablen x₁ ... x₄ ent­spricht. Zwei vorher­gesagten Punkt­ereignissen entspricht dann dasselbe Werte­system der Variablen x₁ ... x₄. Das heißt, die Vorher­sage wird durch die Über­einstimmung der Koordi­naten charakte­risiert. Führt man statt der Variablen x₁ ... x₄ beliebige Funktionen derselben x₁', x₂', x₃', x₄' als neues Koordi­naten­system ein, so dass die Werte­systeme einander ein­deutig zuge­ordnet sind, so ist die Gleich­heit aller vier Koordi­naten auch in dem neuen System der Aus­druck für die raum­zeit­liche Koinzi­denz zweier Punkt­ereignisse. Da sich alle unsere physika­lischen Erfahrungen letzten Endes auf solche Koinzi­denzen zurück­führen lassen, ist zunächst kein Grund vorhanden, gewisse Koordi­naten­systeme vor anderen zu bevor­zugen, das heißt wir gelangen zu der Forderung der all­gemeinen Kovarianz.

§ 4. Beziehung der vier Koordinaten zu räumlichen und zeitlichen Mess­ergebnissen.
Analytischer Ausdruck für das Gravitationsfeld.

Es kam Einstein in dieser Abhandlung nicht darauf an, die Allgemeine Relativi­täts­theorie als ein möglichst einfaches logisches System mit einem Minimum von Axiomen dar­zustellen. Sondern es war sein Haupt­ziel, diese Theorie so zu ent­wickeln, dass der Leser die, wie er sagte, psycho­logische Natür­lich­keit des einge­schlagenen Weges empfindet und dass die zugrunde gelegten Voraus­setzungen durch die Erfahrung mög­lichst gesichert erscheinen. In diesem Sinne sei nun folgende Voraus­setzung einge­führt:
Für unendlich kleine 4-dimen­sionale Gebiete sei die Relativi­täts­theorie im engeren Sinne bei passender Koordi­naten­wahl zutreffend.

Der Beschleunigungs­zustand des unend­lich kleinen, in diesem Fall „örtlichen” Koordinaten­systems sei hierbei so zu wählen, dass ein Gravi­tations­feld nicht auftritt. Dies sei für ein unend­lich kleines Gebiet möglich. Für die weitere Betrachtung seien X₁, X₂, X₃ die räum­lichen Koordinaten. Des Weiteren sei X₄ die zugehörige, in geeignetem Maßstab gemessene Zeit­koordinate. Wobei Einstein noch hinzu­fügt, dass die Zeit­einheit so zu wählen sei, dass die Vakuum-Licht­geschwin­dig­keit, in dem „lokalen” Koordinaten­system gemessen, gleich 1 wird. Diese Koordinaten haben, wenn ein starres Stäbchen als Einheits­maßstab vor­gegeben wird, bei entspre­chender Orien­tierung des Koordi­naten­systems eine unmittel­bare physika­lische Bedeutung im Sinne der Speziellen Relativi­täts­theorie. Damit kann auf Grund­lage der Speziellen Relativitäts­theorie durch Raum-Zeitmessung ein Wert ermittelt werden, der von der Orien­tierung des lokalen Koordinaten­systems unabhängig ist und wie folgt ausge­drückt werden kann: (1)

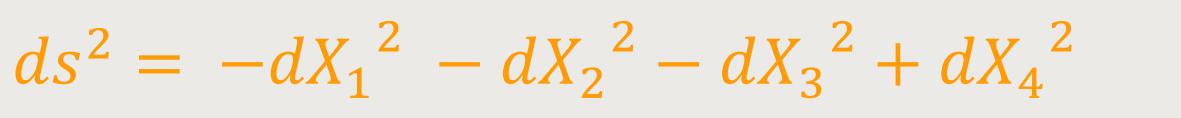
Einstein bezeichnet ds als die Größe des zu den unendlich benach­barten Punkten des 4-dimen­sionalen Raumes gehörigen Linien­elements eines Kurven­verlaufs. Ist das zu dem Element dX₁ ... dX₄ gehörige ds² positiv, so bezeichnet man ersteres nach dem Mathematiker Minkowski „zeitartig”, im entgegen­gesetzten Falle „raumartig”.

Zu dem betrachteten „Linien­element” bzw. zu den beiden unendlich benach­barten Punkt­ereignissen gehören dement­sprechend auch bestimmte Differen­tiale dx₁ ... dx₄ dieser 4-dimen­sionalen Koordinaten des gewählten Bezugs­systems. Ist dieser Umstand sowie ein „lokales” Bezugs­system obiger Darstellung für die betrachtete Stelle gegeben, so werden sich hier die dX_ν durch bestimmte lineare homogene Ausdrücke der dx_σ darstellen lassen: (2)

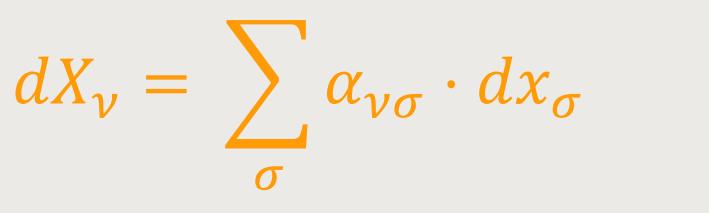
Setzt man diese Ausdrücke in (1) ein, so erhält man: (3)

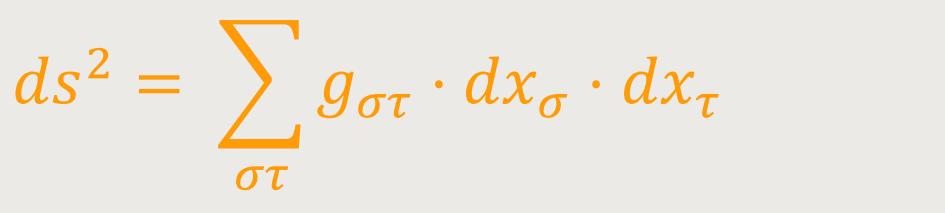
Wobei g_στ Funktionen der x_σ sein werden, die nicht mehr von der Orien­tierung und dem Bewegungs­zustand des „lokalen” Koordinaten­systems abhängen können. Denn ds² ist eine durch Maßstab-Uhren­messung definierte Größe, die ermittelt werden kann. Diese Größe gehört zu den betrach­teten, raum­zeit­lich unendlich benach­barten Punkt­ereignissen, und ist unab­hängig von jeder besonderen Koordi­naten­wahl. Die g_στ sind hierbei so zu wählen, dass g_στ = g_τσ entspricht. Die Summation ist für alle Werte von σ und τ zu ermitteln, sodass die Summe aus 4 × 4 Summanden besteht, von denen 12 paar­weise gleich sind.

Die Situation der gewöhn­lichen Relativi­täts­theorie geht aus dem hier Betrach­teten hervor, falls es unter Berück­sichtigung des besonderen Verhaltens der g_στ in einem endlichen Gebiet möglich ist, das Bezugs­system so zu wählen, dass die g_στ folgende konstante Werte annehmen: (4)

Wir werden später sehen, dass die Wahl solcher Koordinaten für endliche Gebiete im Allgemeinen nicht über­tragbar ist.

Aus den Betrachtungen der § 2 und § 3 geht hervor, dass die Größen g_στ vom physika­lischen Stand­punkt aus als solche Größen anzu­sehen sind, die das Gravi­tations­feld in Bezug auf das gewählte Bezugs­system beschreiben. Angenommen, es sei für ein gewisses betrach­tetes 4-dimen­sionales Gebiet bei geeigneter Wahl der Koordi­naten die Spezielle Relativi­täts­theorie gültig. Dann haben die g_στ die in (4) angegebenen Werte. Ein freier materieller Punkt bewegt sich dann bezüg­lich dieses Systems gerad­linig gleich­förmig. Führt man nun durch eine beliebige Substitu­tion neue Raum-Zeit-Koordinaten x₁ ... x₄ ein, so werden in diesem neuen System die g_μν nicht mehr Konstante, sondern Raum-Zeit-Funktionen sein. Gleich­zeitig wird sich die Bewegung des freien Masse­punktes in den neuen Koordinaten als eine gekrümmte, nicht gleich­förmige darstellen, wobei dieses Bewegungs­gesetz unabhängig von der Natur des bewegten Masse­punktes sein wird. Insofern wird man diese Bewegung als eine solche unter dem Einfluss eines Gravitations­feldes deuten. Damit ist das Auftreten eines Gravi­tations­feldes eng verknüpft mit einer raum­zeit­lichen Veränder­lich­keit der g_στ. Auch für den all­gemeinen Fall, dass sich nicht in einem end­lichen Gebiet bei entspre­chender Koordi­naten­wahl die Gültig­keit der Speziellen Relativi­täts­theorie herbei­führen lässt, hielt Einstein an der Auffassung fest, dass die g_στ das Gravi­tations­feld beschreiben.

Die Gravitation spielt also gemäß der Allgemeinen Relativi­täts­theorie eine Ausnahme­rolle gegen­über den übrigen Kräften, insbe­sondere den elektro­magnetischen Kräften, indem die das Gravitations­feld dar­stellenden 10 Funktionen g_στ zugleich die metrischen Eigen­schaften des 4-dimen­sionalen Messraumes bestimmen.

Hinweis:
In der Physik geht man oft von idealisierten Systemen aus, die man auch als Inertial­system bezeichnet. Im Kosmos und selbst auf der Erde gibt es solche Systeme nicht. Auch wenn wir dies mit unserem bloßen Auge nicht unbedingt wahr­nehmen, befinden wir uns ständig in einem gekrümmten Raum.

⇦ Kapitel Kapitel ⇨