Es ist kein leichtes Unterfangen, die Entfernungen im Weltall zu messen. Da die Abstände im Kosmos gigantisch sind, haben sich Astronomen spezielle Methoden ausgedacht, um die Distanzen zu anderen Sternen und weit entfernten Galaxien zu ermitteln.

Aber wie misst man Entfernungen im Weltall? Selbst zum Nachbar­stern der Sonne sind es schon 40 000 Milliarden Kilometer. Mit anderen Worten, dass Licht benötigt für diese Strecke ca. 4 Jahre.

Um die Distanzen weit entfernter Objekte abschätzen zu können, gehen die Astronomen stufen­weise vor. Zunächst versucht man, möglichst genau die Abstände in unserem Sonnen­system zu ermitteln. Anschließend werden diese Abstände quasi skaliert, wobei die Ausgangs­messungen sehr präzise ausfallen müssen, um Skalierungs­fehler zu vermeiden.

Die erste Stufe der kosmischen Entfernungs­leiter ist der mittlere Abstand, in welchem die Erde um die Sonne kreist. Er beträgt rund 149,6 Millionen Kilometer. Dieser Wert beruht vor allem auf Laufzeit­messungen von Radar­signalen, die von den Ober­flächen der Planeten Merkur, Venus und Mars reflektiert werden. Zusätzlich werden auch Bahn­daten verschiedener Satelliten auf Umlauf­bahnen um diese Planeten ausgewertet.

Heute erreichen sie dabei eine Genauigkeit von nur wenigen Metern. Allerdings ist dabei zu berück­sichtigen, dass wir bei den Gesetzen der Himmels­mechanik keinem Trugschluss erliegen. Ein solcher Trugschluss wäre z. B., wenn die Sonne nicht genau im Zentrum unseres Systems positioniert ist, sondern ebenfalls auf einem Orbit um dieses Zentrum rotiert. Da der Radius im Verhältnis zur Entfernung sehr gering ist, sind die Auswirkungen kaum wahr­nehmbar.

Bei der nächsten Stufe der kosmischen Entfernungs­leiter verlassen wir bereits unser Sonnen­system. Jetzt kommt der sogenannte „Parallaxen­effekt” zum Tragen. Die meisten kennen diesen Effekt aus eigener Erfahrung. Wenn man z. B. aus einem fahrenden Auto die vorbei­ziehende Landschaft betrachtet, verschiebt sich ein Gebäude vor dem weiter entfernten Hinter­grund. Vergleichbar damit betrachten wir im Verlauf eines Jahres den Weltraum von wechselnden Orten aus, wobei die Sterne aus ganz unter­schiedlichen Entfernungen leuchten.

Sterne mit geringeren Entfernungen verändern dadurch ihre Positionen am Firmament im Vergleich zu weit entfernten Sternen im Hinter­grund. Weil aber die Entfernungen so gigantisch sind, verschieben sich ihre Positionen am Himmel im Verlauf eines Jahres nur minimal.

Im Fachjargon bezeichnet man diesen „Wackel­winkel” als Parallaxen­winkel, der erst 1838 von dem Astronomen Friedrich Wilhelm Bessel gemessen wurde. Inner­halb eines halben Jahres verschiebt sich die Position des Sternes 61 Cygni im Stern­bild Schwan um rund 0,6 Bogen­sekunden, das ist der 3600te Teil eines Winkel­grads. Aus dieser winzigen Parallaxe konnte Bessel trigono­metrisch die Entfernung von 61 Cygni berechnen. Sie beträgt rund 100 Billionen Kilometer. Ein Licht­strahl benötigt für diese Strecke fast 11 Jahre.

Als Parallaxe bezeichnet man die scheinbare Änderung der Position eines Objektes durch verschiedene Positionen des Beobachters.

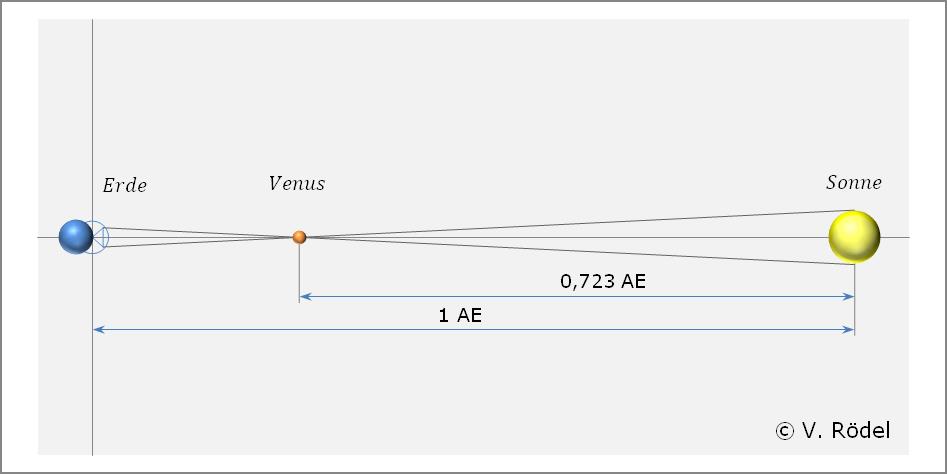
Abb. 1: Berechnen der Entfernung mithilfe der Parallaxe.

Wird ein Objekt (Bezugspunkt) vor einem Hinter­grund (Projektion­sebene) von zwei verschiedenen Positionen (Beobachtungs­punkten) aus betrachtet (Betrachtungs­vektor), so verändert sich die Stelle des Hinter­grunds, vor dem das Objekt optisch liegt (Schnitt­punkt von Vektor und Projektion­sebene). Die Strecke zwischen den Punkten bezeichnet man als „Parallaxe”. Den Abstand zwischen den beiden Beobachtungs­punkten nennt man „Basislinie”, der Richtungs­unterschied zwischen den Vektoren ist der „Parallaxen­winkel” oder parallaktische Winkel. Die Parallaxe ist umso größer, je näher sich das beobachtete Objekt befindet und je länger die Basislinie ist.

Ist die Projektion­sebene nicht klar definiert oder nicht eben, z. B. bei unter­schiedlich weitem Hinter­grund, so bezeichnet Parallaxe üblicher­weise den Winkel.

Hält man z. B. den Daumen aufwärts und betrachtet ihn abwechselnd mit dem linken und dem rechten Auge, so verschiebt sich sein Bild vor dem weiter entfernten Hinter­grund. Die Basis­linie ist hier der Augenabstand, und die Methode heißt „Daumen­sprung”. Der parallaktische Winkel ist bei durch­schnittlicher Armlänge etwa 6 Grad.

Bestimmt man den Parallaxen­winkel mit einem Sensor oder Mess­fernrohr und ist die Basis­linie bekannt, lässt sich die Entfernung zum Zielpunkt genau berechnen.

In der Astronomie wird der Parallaxen­winkel üblicher­weise kurz als „Parallaxe” bezeichnet und die Projektions­fläche ist keine Ebene, sondern die scheinbare Kugel­oberfläche des Sternen­himmels.

Für Distanz­messungen zum Erdmond und nahen Planeten kann bereits der Erd­durchmesser als Basis­linie dienen. So erscheint etwa die Parallaxe der Venus zwischen zwei Beobachtungs­orten auf der Erdkugel in einer leicht verschiedenen Position vor dem Stern­hintergrund. Bei den seltenen Venus­durchgängen vor der Sonne wurde die Parallaxe relativ zum Sonnen­rand gemessen und brachte auf diese Weise erste Werte für den Radius der Erdbahn (die Astronomische Einheit).

Beim Mond beträgt die Parallaxe wegen seiner geringen Distanz maximal 2° d. h., der Mond zieht z. B. von Europa aus betrachtet an völlig anderen Sternen vorbei als in Südafrika. Die Mond­parallaxe ist auch verantwortlich für den unter­schiedlichen Anblick, den eine Sonnen­finsternis von verschiedenen geo­graphischen Breiten aus bietet. So kann man beispielsweise eine zu Hause nur partiell auftretende Finsternis nördlicher oder südlicher als totale Finsternis erleben.

Ein zweites Mess­prinzip ist die Benutzung der Erd­rotation. Auch von einem einzelnen Standort aus entsteht eine Parallaxe, weil der Ort allein durch die Drehung der Erde verschiedene Positionen einnimmt. Die Anwendung dieses Effekts wird „Höhen­parallaxe” genannt. Umgekehrt muss bei genauer Astrometrie dieser Einfluss auf die Messungen als Reduktion korrigiert werden.

Die Parallaxe wird zur Entfernungs­messung sonnen­naher Sterne eingesetzt. Als Basis­linie dient der mittlere Radius der Erdbahn, welcher der großen Halb­achse entspricht. Der Umlauf der Erde ändert die scheinbaren Stern­positionen in Form einer kleinen Ellipse, deren Form vom Winkel abhängt, um den der Stern von der Ekliptik (Ebene der Erdbahn) absteht. Die Parallaxe ist der Winkel, unter dem der Radius der Erdbahn vom Stern aus erscheint. Beträgt die Parallaxe eine Bogen­sekunde (1/3600 Grad), so entspricht das einer Entfernung von 3,26 Lichtjahren oder rund 31 Billionen Kilometern. Diese Entfernung wird auch als eine „Parallaxen­sekunde” (1 Parsec) bezeichnet.

Zur Bestimmung der Entfernung zwischen Sonne und Erde, was einer Astronomischen Einheit (AE) entspricht, gibt es verschiedene Denkansätze. Für die weitere Berechnung verwenden wir in diesem Fall zunächst die Entfernung zwischen Erde und Mars als Grundlage.

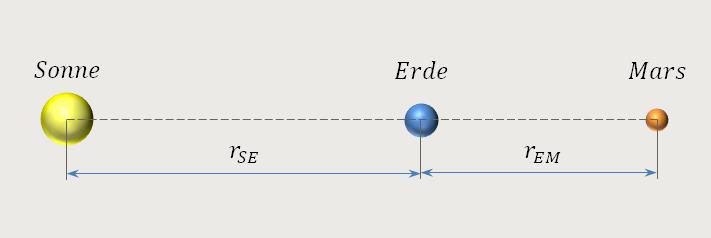
T_E   ist die Umlaufzeit der Erde
T_M   ist die Umlaufzeit des Mars
r_SE   ist der Radius Sonne – Erde
r_EM   ist der Radius Erde – Mars

Die Entfernung von der Erde zum Mars beträgt im Mittel 78,4 · 10⁶ km, wobei die Umlauf­zeit des Mars um die Sonne 1,88 Jahre beträgt.

Das 3. Kepler-Gesetz besagt, dass die Quadrate der Umlauf­zeiten zweier Planeten sich so verhalten, wie die dritten Potenzen der großen Halbachsen:

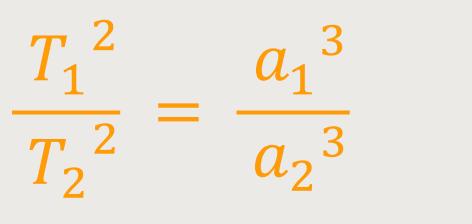
Als erstes setzen wir die Variablen in die Formel ein und ziehen anschließend die dritte Wurzel.

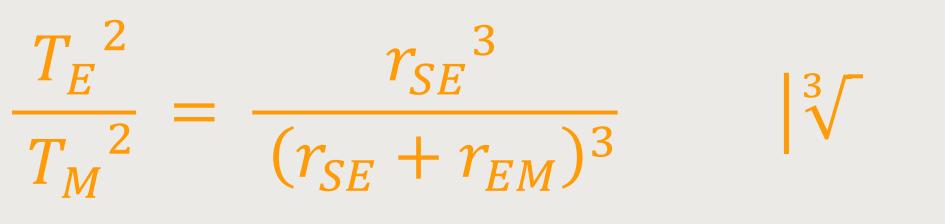
Entsprechend erhält man:

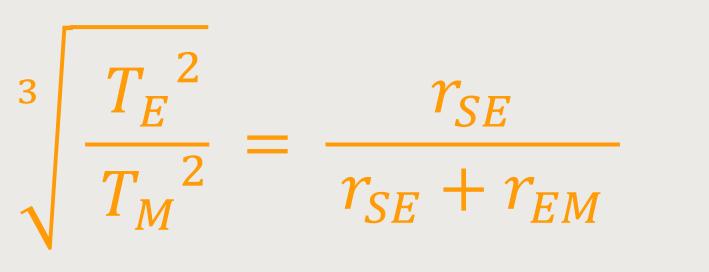
Da wir den Abstand „Sonne – Erde” wissen möchten, müssen wir den Nenner auf die andere Seite bringen.

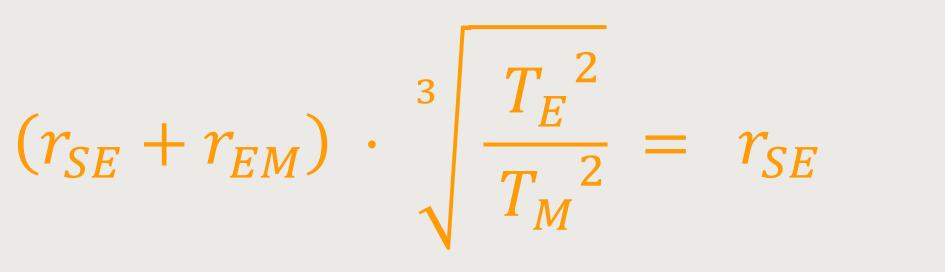
Im nächsten Schritt lösen wir die Summe auf und erhalten:

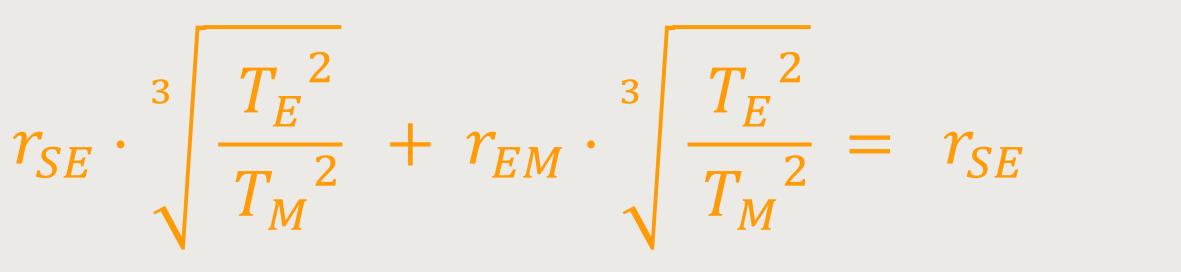
Nun tauschen wir die Terme auf beiden Seiten aus:

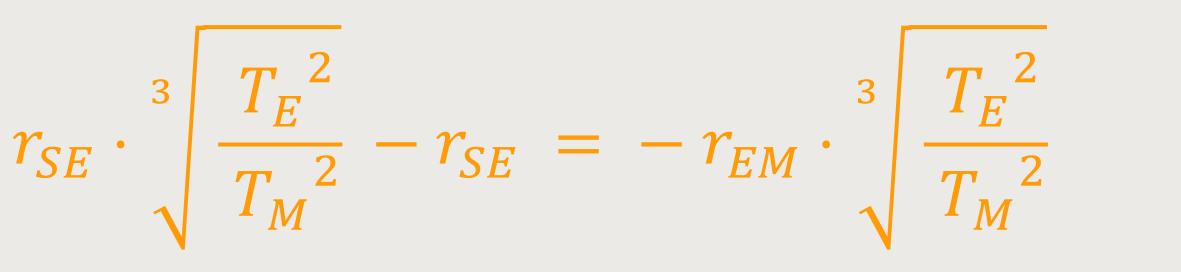
Jetzt bietet es sich an, den Wert aus­zuklammern.

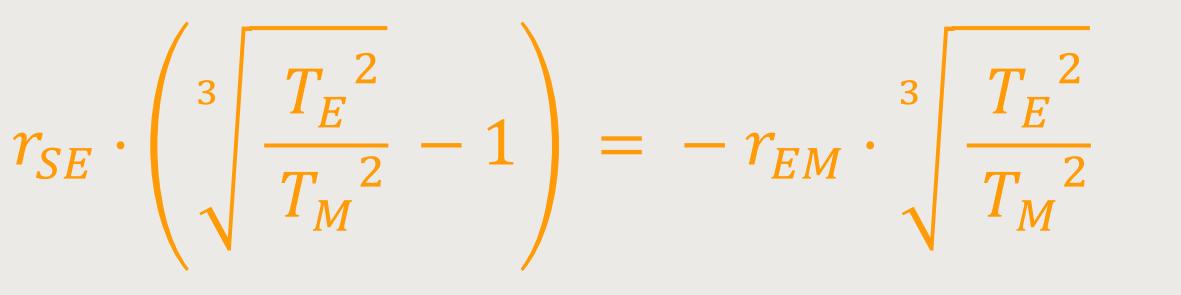
Gesucht wird nach wie vor der Abstand „Sonne – Erde”, weshalb wir den einen Term in den Nenner über­tragen müssen:

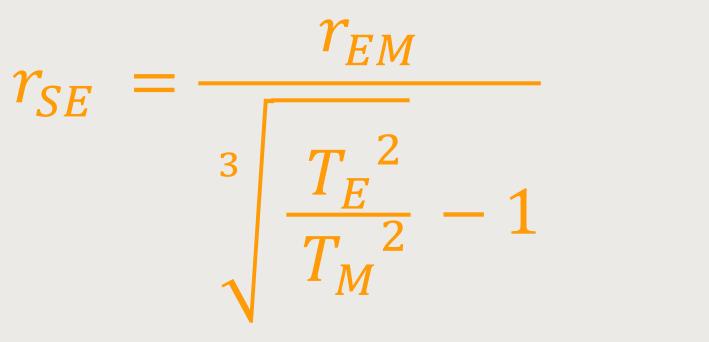
Abschließend müssen wir nur noch die uns bekannten Werte in die Gleichung einsetzen:

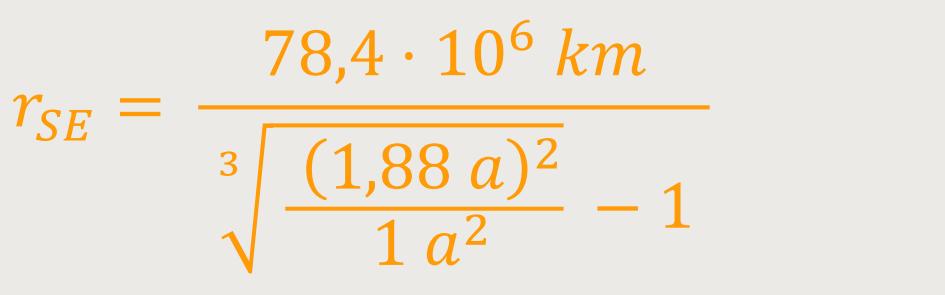
Als Ergebnis erhalten wir:

Die 28. General­versammlung der Inter­nationalen Astronomischen Union beschloss im Jahre 2012, von der bisherigen Definition abzugehen und die Astronomische Einheit einfach als eine Strecke der Länge neu zu definieren. Der genaue Wert, der diesbezüglich festgelegt wurde, und damit einer AE (Astrono­mischen Einheit) entspricht, beträgt:

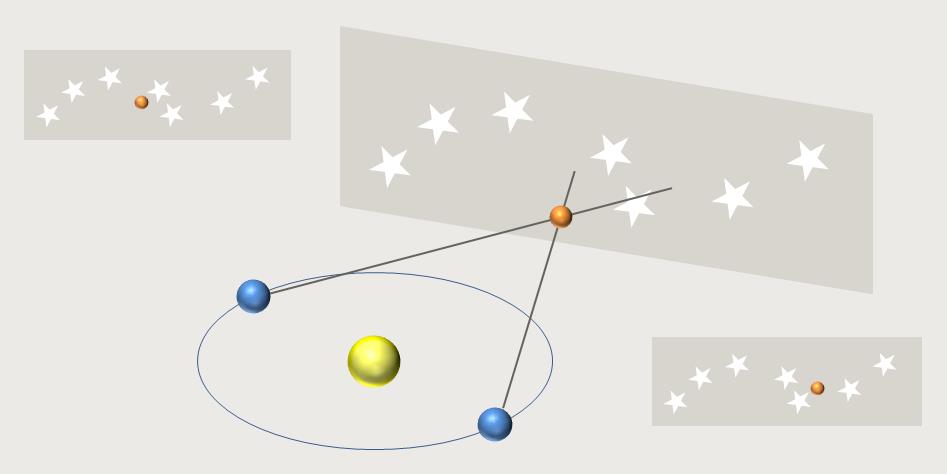
Abb. 3: Das Prinzip der Sternparallaxe im Halbjahresrythmus

Bei Sternen, die weiter entfernt sind als 300 Licht­jahre, versagt die geometrische Entfernungs­messung der Parallaxe, wenn sie von der Erde aus durch­geführt wird. Die parallak­tischen Positions­änderungen sind dann zu klein, um sie mit einem Teleskop nachweisen zu können. Das liegt vor allem an der turbulenten Luft­hülle der Erde.

Aus diesem Grund hat man den Astro­metries­atellit „Gaia” im Orbit platziert, der den Stern­himmel vom Weltall aus kartiert. Die Sonde dreht sich pro Tag viermal um ihre eigene Achse, sodass ihre CCD-Detektoren tagtäglich die Positionen von rund 40 Millionen Sternen gestochen scharf erfassen. Auf diese Weise wird die Position jedes Sterns bis zu 70-mal gemessen. Anschließend werden die Sternpositionen zu winzigen Parallaxen­kringeln zusammen­gefügt.

Durch diese Langzeit­beobachtung konnte mithilfe der umfangreichen Daten ein 3-dimensionaler Stern­atlas erstellt werden. Er zeigt die genaue räumliche Verteilung von 1,3 Milliarden Sternen in unserer kosmischen Nachbarschaft innerhalb der Milch­straße. Der sogenannte „Gaia-Atlas” umfasst dabei Sterne mit Entfernungen von bis zu 10 000 Lichtjahren.

Doch das ist garnichts im Vergleich zu unserer Milch­straße, die nach neuesten Messungen rund 200 000 Licht­jahre groß ist. Die benachbarte Andromeda-Galaxie ist bereits 2,5 Millionen Licht­jahre entfernt, und sie ist nur eine von unzähligen gigantischen Stern­wolken.

Bei den weiteren Stufen auf der kosmischen Leiter stützen sich Wissen­schaftler auf dem Aspekt der Licht­ausbreitung bzw. Licht­ermüdung. Je weiter ein Stern von uns entfernt ist, desto weniger kommt des von ihm abgestrahlten Lichts noch bei uns an.

Die Intensität des ankommenden Lichts eines Sterns nimmt mit dem Quadrat seiner Entfernung ab. Ein Stern, der doppelt so weit entfernt von uns ist wie ein vergleich­barer Stern, leuchtet nicht mit halber Intensität am Nacht­himmel, sondern erreicht nur noch ein Viertel von dessen Intensität.

Um aus diesem photo­metrischen Entfernungs­gesetz die Distanz zu einem Stern berechnen zu können, muss man seine Leucht­kraft kennen. Es geht also um die Frage, wie viel Licht strahlt er tatsächlich ab. Man hat heraus­gefunden, dass es bestimmte Sorten von Sternen gibt, denen eine spezifische Leucht­kraft zugewiesen werden kann.

Vor rund 100 Jahren wurde die US-amerikanische Astronomin Henrietta Swan Leavitt auf eine dieser Stern­sorten aufmerksam. Mithilfe der damaligen Computer wurden die Positionen, Hellig­keiten und Farben der vielen Sterne, die auf Fernrohr­aufnahmen des Himmels zu sehen waren, geordnet und katalogisiert.

Als sich H. Leavitt auf die „Kleine Magellansche Wolke” konzentrierte, eine Zwerggalaxie, in der rund 5 Milliarden Sonnen leuchten, konnte H. Leavitt auch einige Cepheiden aufspüren. Diese Sterne verändern sich regelmäßig nach einem ähnlichen Muster. Deren Helligkeit steigt innerhalb weniger Tage oder Wochen ein wenig an und fällt dann langsam wieder ab.

H. Leavitt bemerkte, dass alle Sterne in dieser Galaxie einschließlich der Cepheiden aufgrund des Betrachtungs­winkels ungefähr aus der gleichen Entfernung zu uns herüber­leuchten. Somit waren die verschiedenen Helligkeiten der Sterne auf den Foto­platten, nicht auf unter­schiedliche Entfernungen zurück­zuführen, sondern tatsächlich strahlte ein als heller Stern klassifizierter Cepheide auch mehr Licht ab als ein Cepheide, der weniger gut zu sehen war.

Auf diese Weise konnte ein Zusammen­hang zwischen der jeweiligen Helligkeit eines Cepheiden und der Perioden­dauer, mit der seine Helligkeit schwankt, abgeleitet werden. Je mehr Licht ein Cepheiden-Stern abstrahlt, desto länger dauert eine Periode seiner Helligkeits­schwankung.

Die Datenanalyse ergab aller­dings nur, wie hell ein Cepheide mit einer bestimmten Pulsations­dauer im Vergleich zu einem weiteren Cepheiden leuchtet, der eine andere Pulsations­dauer besitzt. Eine Aussage über die Leucht­kraft der Cepheiden konnte damit noch nicht angegeben werden.

Erst einige Jahre später gelang es dem dänischen Astronomen Ejnar Hertzsprung, aus den Daten von 13 Cepheiden innerhalb der Milch­straße, die in einem Stern­katalog aufgeführt waren, deren geometrische Parallaxen zu berechnen und daraus wiederum ihre Entfernungen. Der Katalog verzeichnete ebenso die beobachteten Helligkeiten dieser Sterne. Und deshalb konnte Hertzsprung mithilfe ihrer nun bekannten Entfernungen und dem photo­metrischen Entfernungs­gesetz auch die tatsächlichen Leucht­kräfte dieser Cepheiden ermitteln. Durch die Umkehr­rechnung war es möglich heraus­zufinden, wie viel Licht sie wirklich abstrahlen.

Jetzt konnte man jeder beobachteten Perioden­dauer, mit der ein Cepheide seine Helligkeit verändert, eine spezifische Leucht­kraft zuordnen, also wie viel Licht der Stern tatsächlich abstrahlt. Aus dem Vergleich dieser Leucht­kraft mit der beobachteten Helligkeit des auf der Erde ankommenden Lichts konnte man direkt die Entfernung des entsprechenden Cepheiden berechnen.

Weitere zehn Jahre später erkannte Edwin Powell Hubble mit dem damals größten Fernrohr der Welt, dass der so genannte „Andromeda-Nebel” in Wahrheit aus Milliarden von Sternen besteht. Unter diesen Sternen konnte er sogar einige Sterne als Cepheiden entlarven. Schon beim ersten Stern, den Hubble als Cepheiden erkannte, bestimmte er eine lange Periode der Helligkeits­variation von 31,41 Tagen.

Auf Grundlage der Perioden-Leuchtkraft-Beziehung musste es sich also um einen Cepheiden mit sehr hoher Leucht­kraft handeln. Von der Erde aus war davon aller­dings nicht mehr viel zu sehen. Aus dieser geringen Helligkeit berechnete Hubble eine enorme Entfernung des Cepheiden, und damit auch die Entfernung der Andromeda-Sternwolke. Nach heutigem Wissen ist sie besagte 2,5 Millionen Licht­jahre entfernt.

Derartige Sternwolken, die aus vielen 100 Milliarden Sternen bestehen, bezeichnen wir heute als „Galaxien”. In der Zwischen­zeit haben die Astronomen in einer Viel­zahl von Galaxien Cepheiden aufgespürt, und konnten mit diesem Verfahren ihre Helligkeiten und die Perioden­dauer der Helligkeits­variationen messen. Daraus wurden ihre Leucht­kräfte bestimmt und letzten Endes die entsprechende Entfernung der Galaxien berechnet.

Mit den Daten des Astrometrie-Satelliten Gaia konnte die Präzision weiter erhöht werden, und die Leucht­kraft der Cepheiden noch präziser kalibriert werden. Würde es diese pulsierenden Cepheiden nicht geben, hätten sich Astronomen ein anders Mess­verfahren einfallen lassen müssen.

Nun war es an der Zeit, eine weitere Stufe der Entfernungs­messung zu erklimmen. Man konnte nämlich beobachten, dass in diesen Galaxien gelegentlich Sterne mit extrem großer Leucht­kraft aufleuchten. Genau genommen sieht man dabei nicht mehr das Licht dieser Sterne selbst, sondern das Licht der Explosion, bei der diese Sterne am Ende ihrer Existenz zerbersten. Es handelt sich dabei um eine sogenannte „Supernova-Explosion Typ 1a”, wobei der explodierende Ausgangs­stern immer ein Weißer Zwerg­stern in einem Doppelstern­system ist.

Eine weitere Voraussetzung die erfüllt sein muss besteht darin, dass die beiden Sterne so eng umeinander herum kreisen müssen, dass vom zweiten Stern ununter­brochen Materie auf den Weißen Zwerg hinüber­strömt. Dadurch nimmt die Masse des Weißen Zwergs immer mehr zu, und irgend­wann wird dieser Stern unter seinem wachsenden eigenen Gewicht so stark zusammen­gepresst und heiß, dass er explodiert.

Da die Explosion stets bei der gleichen Grenz­masse von etwa 1,4 Sonnen­massen eintritt, ist auch die erreichte Leucht­kraft des Explosions­lichts annähernd gleich groß. Aus der beobachteten Helligkeit des Explosions­lichts und seiner bekannten Entfernung kann dann auf die Leucht­kraft der Stern­explosion zurück­gerechnet werden.

Die so kalibrierte Leuchtkraft einer Super­nova vom Typ 1a ist rund 5 Milliarden Mal größer als die Leucht­kraft der Sonne. Deshalb können diese Stern­explosionen auch dann noch beobachtet werden, wenn sie in sehr weit entfernten Galaxien aufleuchten. Und aus der geringen Helligkeit, mit der das Licht der jeweiligen Supernova noch die Erde erreicht, kann wiederum ihre Entfernung und damit auch die Entfernung ihrer Heimat­galaxie berechnet werden.

Nicht ohne Grund bezeichnet man die Supernova-Explosionen vom Typ 1a als sogenannte „Standardkerzen”. Denn mit diesem Wissen lassen sich immer zuverlässigere Aussagen über die Strukturen des Kosmos machen. Diese Standard­kerzen haben uns unter anderem bestätigt, dass sich der 4-dimensional gekrümmte Raum gegen­wärtig ausdehnt, und dies sogar mit zunehmender Expansions­rate.

Wie wir in den vorherigen Kapiteln gesehen haben, ist dieser Effekt auf die Wirbel­strukturen und dem kosmischen Zeit­strahl im Universum zurück­zuführen. Das führt letztlich dazu, dass die Abstände zwischen den Galaxien beschleunigt anwachsen.

... Fortsetzung folgt ...

Gegenwärtig wird die mathematische Beweis­führung zusammen­gestellt, dass die Sonne, ähnlich wie die anderen Planeten, einen spezifischen Orbit um das Zentrum unseres Sonnen­systems beschreibt. Damit ist nicht der Schwer­punkt gemeint. Die Entfernung der Sonne zu diesem Zentrum ist zwar im Verhältnis zu den Planeten und deren Entfernung sehr gering, aber dennoch vorhanden.

Das Postulat der „Wirbelstrukturen im Kosmos” und insbesondere „im Sonnen­system”, und vor allem die mathematische Funktion, welche die Orbital­geschwindigkeiten beschreibt, lässt keinen anderen Schluss zu.

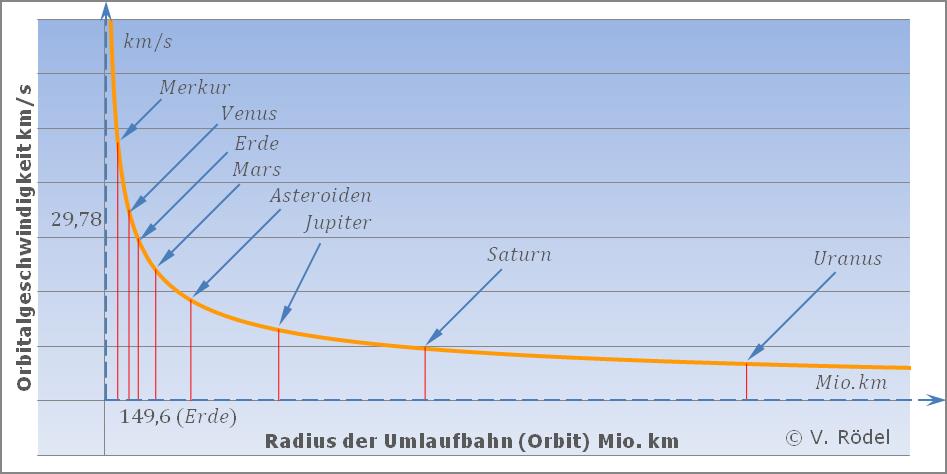
Abb. 4: Die Orbitalgeschwindigkeiten der Planeten

⇦ Kapitel Kapitel ⇨