Jetzt ist es an der Zeit, wie ver­sprochen ein neues physika­lisches Modell zu präsen­tieren. Wir möchten hier­bei wie gewohnt Schritt für Schritt vor­gehen, um die Über­legungen nach­voll­ziehen zu können.

Wie wir uns viel­leicht erinnern, beschrieb Isaac Newton in seiner Principia als erster die Gravi­tation mithilfe einer mathe­matischen Formel. Dieses von ihm formu­lierte Gravi­tations­gesetz ist eine der Grund­glei­chungen der klas­sischen Mechanik. Es war die erste physika­lische Theorie, die man auch in der Astro­nomie anwandte. Newton bezeich­nete die Gravi­tation als eine Kraft, die zwischen zwei Körpern wirkt und diese zu ihrem gemein­samen Schwer­punkt hin beschleu­nigt. Wobei die Stärke der Gravi­tation propor­tional zum Quadrat des Abstandes der Körper abnimmt.

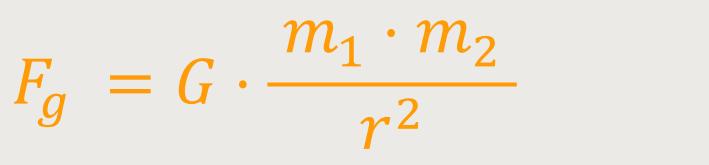
Abb. 1: Das Newton'sche Gravitationsgesetz.

In der 1916 von Albert Einstein auf­ge­stellten Allge­meinen Relativi­täts­theorie (ART) wird die Gravi­tation jedoch auf eine geome­trische Eigen­schaft der Raum­zeit zurück­geführt. Nach seiner Auf­fassung wird die Raum­zeit durch die Anwesen­heit von Masse und jeglicher Form von Energie gekrümmt. Durch diese Sicht­weise ist es mög­lich, die Gravi­tation grund­sätz­lich anders zu inter­pretieren als die anderen Kräfte. Die Gravi­tation lässt sich dann als Trägheits­kraft ansehen.

Somit wurde Newtons Gravi­tations­gesetz durch die Allge­meine Relativi­täts­theorie (ART) auf den Prüf­stand gestellt.

Und nach wie vor stellt das „Dreikörper­problem” eines der größten Heraus­forde­rungen dar, welches aus der Betrach­tung der Himmels­mechanik ent­steht. Das Problem besteht näm­lich darin, die Wechsel­wirkung dreier physika­lischer Systeme, in diesem Fall die Bewegung von drei Himmels­körpern unter dem Ein­fluss ihrer gegen­seitigen Massen­anziehung auf der Basis des Newton'schen Gravi­tations­gesetzes zu berechnen.

Das Dreikörper­problem gilt seit den Ent­deckungen von Johannes Kepler und Nikolaus Kopernikus als eines der schwie­rigsten mathe­matischen Probleme. Um quanti­tative Resultate zu erlangen, ist das Problem bisher im allge­meinen Fall nur numerisch zu lösen. Trotz der Bemü­hungen großer Mathe­matiker seit mehr als zwei Jahr­hunderten konnte noch keine all­gemeine Lösung angegeben werden. Selbst ein allge­meines Näherungs­verfahren wurde bislang nicht gefunden.

Die grund­sätzliche Heraus­forderung besteht nach wie vor darin, dass es keine weiteren Bewegungs­integrale gibt, die aus den uns bekannten Erhaltungs­sätzen herzu­leiten wären. Letzt­lich sind nur algebraische bzw. ein­deutige analytische Funk­tionen der Orte und Geschwindig­keiten der Himmels­körper möglich.

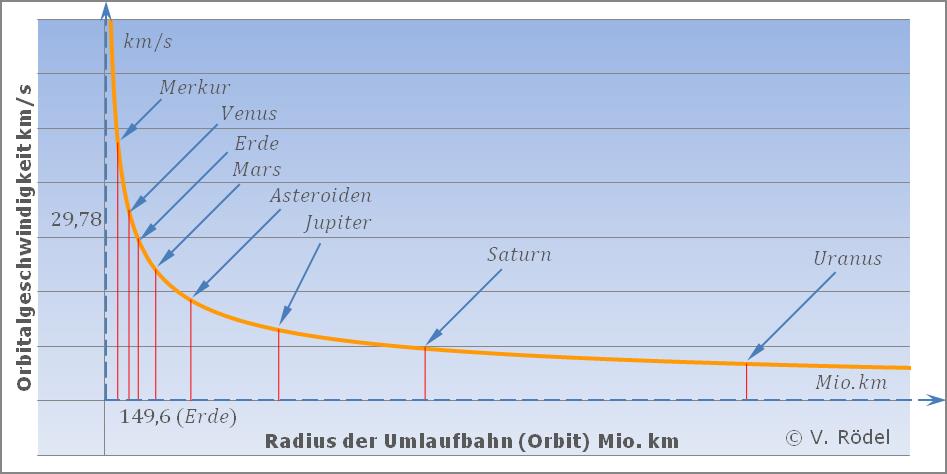
Alle Planeten unseres Sonnen­systems, einschließlich der Sonne selbst, kreisen um ein gemein­sames Zentrum. Man sagt zu Recht, dass die Sonne zwar unser Zentral­gestirn ist, aber die Sonne ist nicht der Mittel­punkt unseres Sonnen­systems. Das eigent­liche Zentrum ist nicht mit dem Schwer­punkt der Sonne identisch. Für jeden Planeten, einschließ­lich der Sonne, gilt eine spezi­fische Orbital­geschwindigkeit.

Schaut man in der Fach­literatur nach, so weichen die Angaben mitunter gering­fügig von­einander ab. Für den Laien mag dies verwunder­lich wirken. Doch bei unserem Sonnen­system handelt es sich um ein dynamisches „Uhrwerk”, das in einem 4-dimen­sionalen Raum seine Bahnen zieht. Jede aktuelle Messung wird daher von der vorher­gehenden gering­fügig abweichen.

Für die weiteren Über­legungen gehen wir von den aktuellen Werten aus. Uns interes­sieren dabei vor allem die Orbital­geschwindig­keiten, und die mittlere Ent­fernung der Himmels­körper um das Zentrum unseres Sonnen­systems:

Himmels- körper  (Planeten)	mittlere  Entfernung Mio. km	Orbital-  geschwindig- keit km/s
Sonne	2,543	229,6
Merkur	57,909	47,36
Venus	108,159	35,02
Erde	149,597	29,78
Mars	227,987	24,07
(Asteroiden)	321 ... 485	20 ... 16
Jupiter	778,507	13,06
Saturn	1433,447	9,68
Uranus	2872,429	6,81
Neptun	4494,967	5,43
(Kuiper-   gürtel)	5906 ... 10173	3,6 ... 4,7

Trägt man obige Werte in ein Diagramm ein, so ergibt sich ein Kurven­verlauf, der wie nicht anders zu erwarten, einen hyper­bolischen Charakter aufweist.

Abb. 2: Die Orbitalgeschwindigkeiten der Planeten.

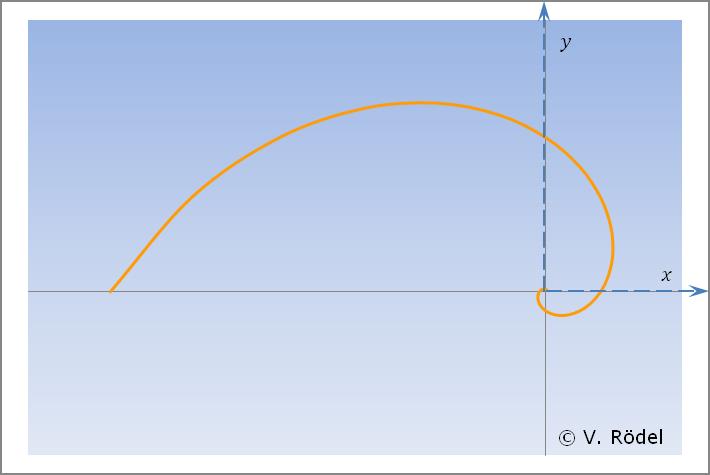
Was spricht dagegen, diesen Kurven­verlauf auf einen soge­nannten „Potential­topf” zu über­tragen, in welchem die Planeten, einschließlich der Sonne, inner­halb von Potential- bzw. Energie­feldern ihre Bahnen ziehen?

Wenn das zutreffend ist, müsste sich der Potential­verlauf eben­falls in Form einer Spiral­kurve dar­stellen lassen.

Abb. 3: Die Kosmos-Spirale (rechtsdrehend).

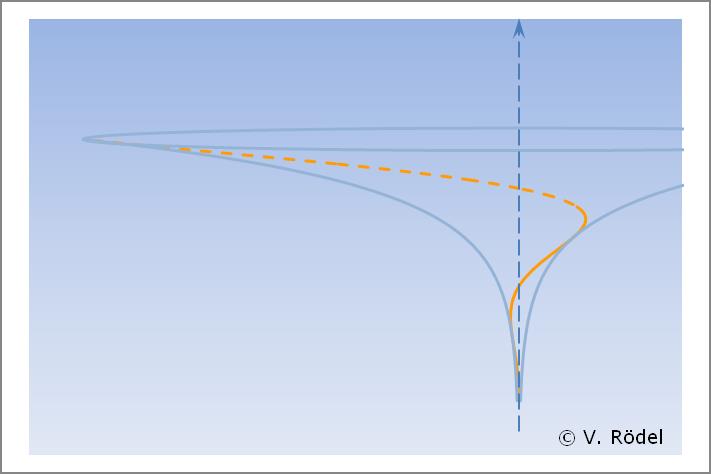
In der Seiten­ansicht ent­spricht dies einem hyper­bolischen Trichter, ähnlich wie bei einem „Schwarzen Loch”.

Abb. 4: Kosmos-Spirale (rechtsdrehend) in positiver Richtung zunehmend;
mit hyperbolischer Form (in y-Richtung gestaucht dargestellt).

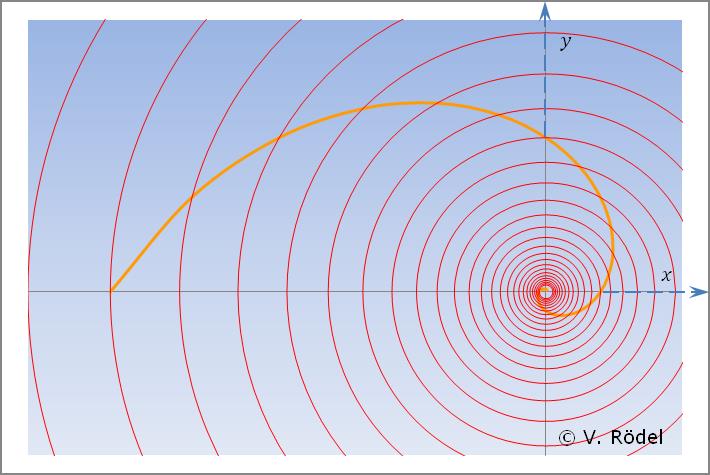
Auf diese Weise werden Potential- bzw. Energie­felder beschrieben, deren Potential nach außen hin abnimmt, ähn­lich wie dies bei einem Potential­topf der Fall ist. Dement­spre­chend nimmt die kinetische Energie zum Zentrum gerichtet zu.

Jedes dieser Potential­felder lässt sich durch eine imaginäre Linie abgrenzen. Die Masse­teilchen, die sich in den jewei­ligen Energie­feldern befinden, würden ohne eine Gegen­kraft in das Zentrum hinein­spiralen. Das Gleiche würde auf unsere Planeten zutreffen. Doch über die Jahr­millionen hat sich ein Kräfte­gleich­gewicht eingestellt.

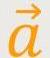Die „Normal­beschleu­nigung” _n, die zum Kreis­mittel­punkt gerichtet ist, nennt man auch die „Zentri­petal­beschleu­nigung”.

Bei einer Kreis­bewegung mit konstanter Winkel­geschwindig­keit wird es keine Tangential­beschleu­nigung geben. In diesem Fall gibt es nur eine Normal­beschleu­nigung. Und daher bleibt auch der Betrag des Geschwindig­keits­vektors konstant. In diesem Zusammen­hang gibt es noch die „Zentri­fugal­kraft”. Darunter ver­steht man eine Trägheits­kraft, die in bewegten und beschleu­nigten Bezugs­systemen eine Rolle spielt.

Wenn man, wie in unserem Fall, ein rotierendes Bezugs­system betrachtet, wirkt auf die Masseteil­chen, sprich die Planeten, eine „nach außen” gerichtete Trägheits­kraft, näm­lich diese Zentrifugal­kraft. Und die Zentripetal­beschleu­nigung ruft ihrer­seits eine entspre­chende „nach innen” gerich­tete „Zentripetal­kraft” hervor, die not­wendig ist, um die nach außen gerichtete Zentri­fugal­kraft zu kompen­sieren, sodass die Planeten nicht „hinaus­fliegen”.

Da sich die Sonne ihrer­seits eben­falls in einem Kräfte­gleich­gewicht befindet, und die Größen­ordnung der Gravi­tations­kraft ver­schwindend gering ist, übt sie keinen nennens­werten Ein­fluss auf die Erde aus. Wie lässt sich sonst erklären, dass die Erde mittler­weile nicht in die Sonne hinein­spiralt ist, wenn doch die Masse der Sonne zur­zeit sage und schreibe etwa das 333.000-fache der Masse der Erde beträgt?

Wie stark die Raum­krüm­mung in einem solchen Potential­trichter aus­fällt, hängt maß­geblich von dem Gesamt­dreh­impuls des rotierenden Systems ab. Dementspre­chend kann er um ein Viel­faches flacher aus­fallen, sodass beispiels­weise die Ekliptik unseres Planeten­systems sehr „eben” erscheint.

Abb. 5: Darstellung der Energiefelder in einem Potentialtopf.

Letztlich spielt es aber keine Rolle, wie gekrümmt der Raum ist. Da der Formalismus eine gekoppelte quadra­tische Funktion bein­haltet, bleiben die Potential­felder für sich betrachtet immer erhalten. Dementspre­chend lassen sich diese grafisch darstellen. Jedes Potential­feld spiegelt die kinetische Energie der darin befindlichen Masseteilchen wider.

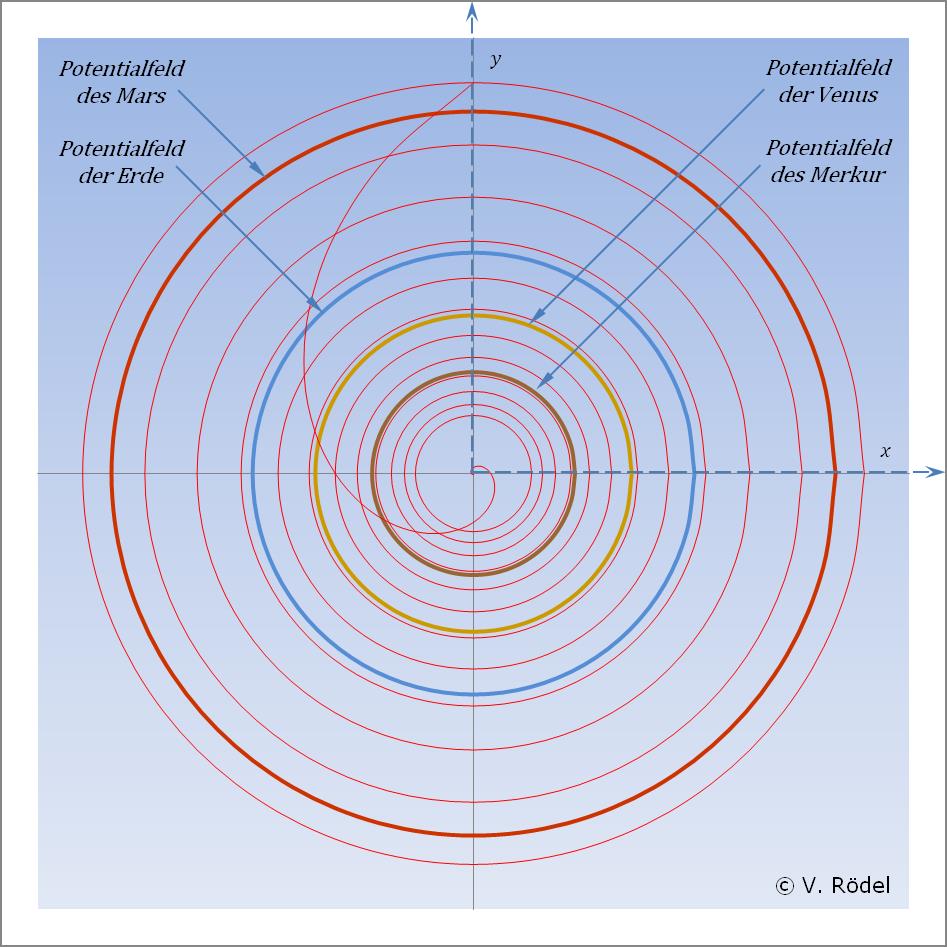
Bei der nachfolgenden Betrach­tung lassen wir die „Gravi­tation” völlig außen vor, und konzen­trieren uns auf den Potential­verlauf, der durch die Spiral­kurve visuali­siert wird. Die sich daraus ergebenden Grenz­linien der Potential- bzw. Energie­felder lassen sich ganz einfach auf unser Sonnen­system über­tragen.

Abb. 6: Die Potentialfelder Merkur bis Mars.

Es fällt auf, dass sich die Orbits der Planeten trotz ihrer leicht ellip­tischen Bahnen immer inner­halb eines solchen Potentials befinden. Das sollte man auch erwarten, wenn diese Neue Theorie zutreffend ist.

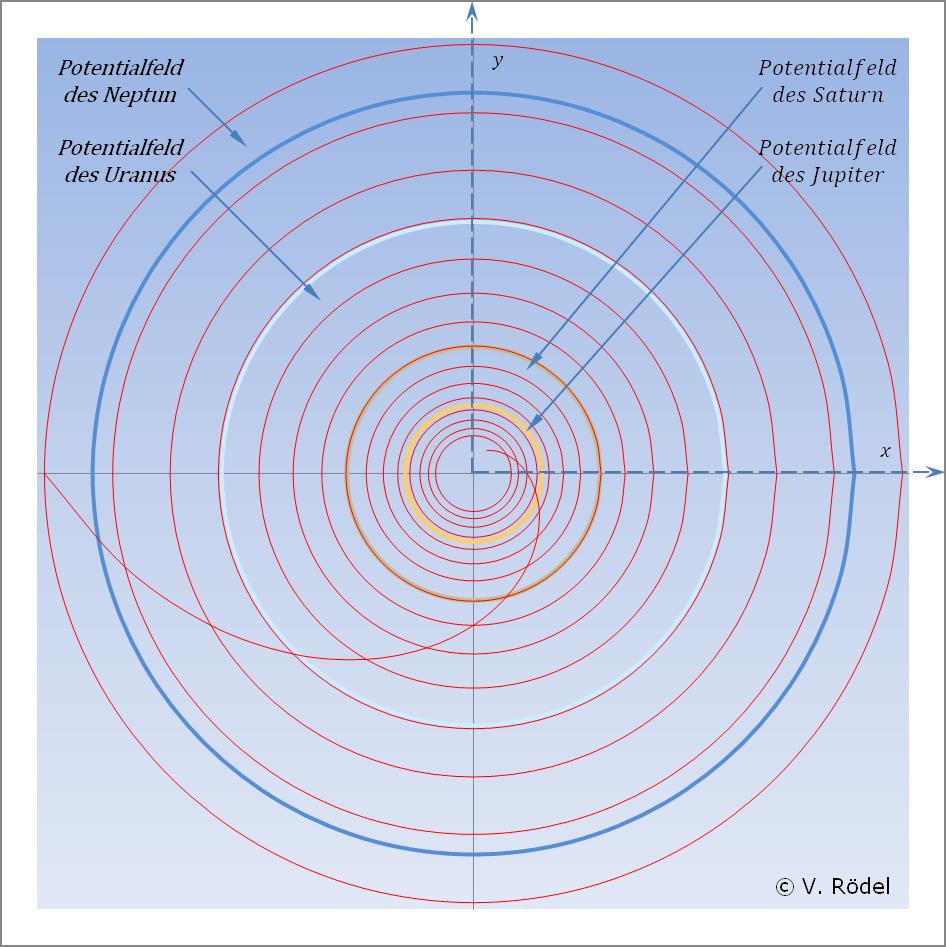
Das Gleiche trifft auch auf die weiter außen liegenden Planeten zu.

Abb. 7: Die Potentialfelder von Jupiter bis Neptun.

Jetzt mag man aller­dings einwenden: Befinden sich die Planeten­bahnen denn nicht immer in irgend­einem dieser Potentiale; wenn nicht in diesem dann eben in dem benachbarten?

Auf den ersten Blick scheint dieses Argument zutreffend. Aller­dings weist unser Sonnen­system dies­bezüg­lich eine Besonder­heit auf. Dabei handelt es sich um den Asteroiden­gürtel, der sich zwischen Mars und Jupiter ein­reiht. Es ist nicht irgendein breiter Gürtel, der sich irgendwo auf der Ekliptik befindet.

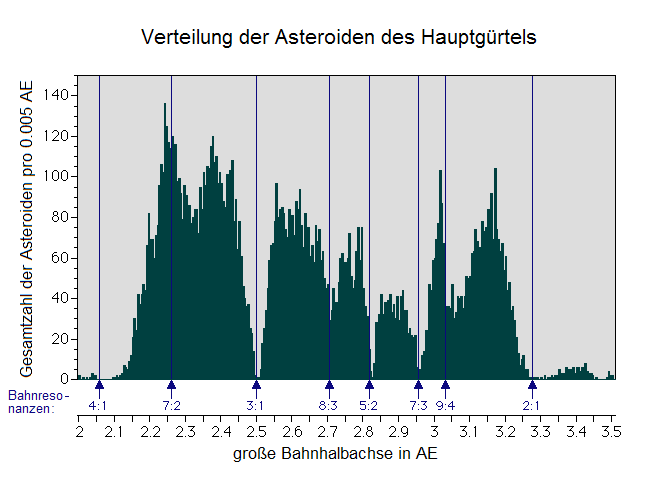
Es lässt sich näm­lich eine Dichte­verteilung der Asteroiden im Haupt­gürtel nach­weisen.

Abb. 8: Verteilung der Asteroiden im Hauptgürtel © NASA.

Die Skala zeigt den Abstand der einzelnen Gruppen zur Sonne in AE (Astronomische Einheit). Der Haupt­gürtel lässt sich im Wesent­lichen in drei Bereiche auf­teilen.

Die „Flora-Familie” ist eine relativ große Gruppe von Asteroiden der S-Klasse im inneren Gürtel (2,15...2,35 AE). Ihre Bahnen weisen eine Neigung von 1,5...8° auf. Etwa 4-5 % aller Haupt­gürtel­asteroiden gehören zu dieser Gruppe.
Zur „Vesta-Gruppe” gehören Planetoiden mit Bahn­neigungen von 5...8° in einer Ent­fernung von 2,25...2,5 AE. Sie gehören meist der V-Klasse an. Etwa 6 % aller Haupt­gürtel­asteroiden gehören zu dieser Familie, deren bekanntestes und größtes Mit­glied der Namens­geber „Vesta” ist.
Die „Nysa-Gruppe” liegt in einer ähn­lichen Ent­fernung wie die Vesta-Asteroiden, jedoch weisen ihre Mit­glieder Bahn­neigungen von nur 1...5° auf. In der Nähe befinden sich auch Objekte der „Massalia-Gruppe”, deren Bahnen nur um 0...2,5° geneigt sind.

Eine weitere große Gruppe wurde nach dem Asteroiden „Eunomia” benannt und erstreckt sich hinter der „Hestia-Lücke” mit Bahn­halbachsen von 2,5...2,8 AE. Die Objekte gehören meist der S-Klasse an und besitzen Bahn­neigungen von 11...16°. Mit über 4600 Mitgliedern gehören etwa 5 % aller Haupt­gürtel­asteroiden zu dieser Familie.
Die „Gefion-Familie” befindet sich in Ent­fernungen von 2,7...2,8 AE. Die Bahn­neigung der Mitglieder, die überwiegend zur S-Klasse gehören, beträgt 7,5...10,5°. Inner­halb der Gruppe liegt die Bahn des Zwerg­planeten „Ceres”, der jedoch nicht zu dieser Familie gehört, da sich seine Zusammen­setzung deutlich von der der anderen Objekte unter­scheidet.

Die Objekte der „Koronis-Gruppe” besitzen geringe Bahn­neigungen von 0...3,5°. Sie stellen die Mehr­heit der Asteroiden, die sich in einer Ent­fernung von 2,8...2,95 AE befinden, und werden von den Zonen, auf denen eine 5:2- bzw. 7:3-Resonanz zu Jupiter herrscht, begrenzt. Das bekannteste Mitglied der Familie ist der Asteroid (243) „Ida”.
Die „Eos-Gruppe” liegt in einer Ent­fernung von 2,99...3,03 AE und weist Bahn­neigungen von 8...12° auf.
Die „Themis-Familie” enthält Asteroiden mit Bahn­halbachsen von 3,08...3,24 AE und Bahn­neigungen mit weniger als 3°.
Zur „Hygiea-Gruppe” zählt ca. 1 % der Haupt­gürtel­asteroiden. Sie befinden sich in ähn­licher Ent­fernung wie Asteroiden der Themis-Gruppe, haben aller­dings eine stärkere Bahn­neigung von 4...6°. Die Mit­glieder sind meist Objekte der B- und C-Klasse.

Abb. 9: Verteilung der Asteroiden im Hauptgürtel (Quelle: Wikipedia).

Frage: Wie kommt es zu den nach­weislich vor­handenen Lücken in dem Asteroiden­gürtel? Diese nach­haltige Frage lässt sich mit der nach­folgenden Grafik beantworten.

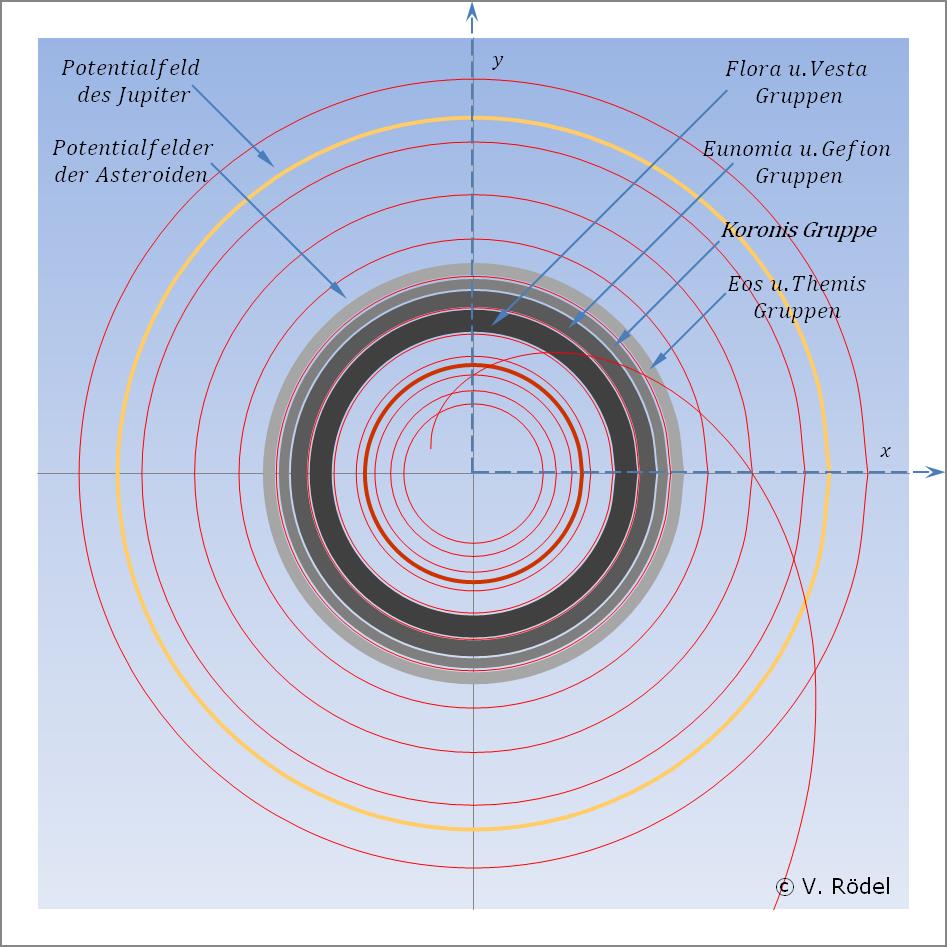
Ordnet man die zuvor beschriebenen Teil­bereiche des Haupt­gürtels in den zuvor beschriebenen Potential­feldern an, fallen sofort zwei Besonder­heiten auf:

1.) Jeder Teil­bereich des Haupt­gürtels, sprich der „Innere”, der „Mittlere” und auch der „Äußere” Haupt­gürtel liegen trotz ihrer enormen Ausdehnungen genau inner­halb eines Potential- bzw. Energie­feldes.

2.) Die „Lücken” dagegen liegen genau auf den Grenz­linien der Potentalfelder des postulierten Potential­topfes.

Abb. 10: Die Potentialfelder der Asteroiden.

Sollte das alles nur reiner Zufall sein? Oder ist das womöglich die Antwort auf die immerwährend gestellte Frage zu einer Alter­native der Gravitation? Wenn das tatsächlich der Fall ist, muss sich dieses neue Verständnis auch auf unseren Kosmos übertragen lassen.

In einem späteren Kapitel werden wir diese Theorie auf unsere Galaxien und deren innere Strukturen über­tragen. Es werden dabei weitere verblüffende Details zutage gefördert.

⇦ Kapitel Kapitel ⇨