Die Navier-Stokes-Gleichungen, benannt nach Claude L.M.H. Navier und George G. Stokes, sind ein mathematisches Modell, um Strömungen von linear-viskosen Flüssigkeiten und Gasen (Fluiden) zu beschreiben. Die Gleichungen der beiden Mathematiker und Physiker sind eine Erweiterung der Euler-Gleichungen der Strömungsmechanik, bei denen es um die Viskosität beschreibende Terme geht.
Im engeren Sinne, insbesondere in der Physik, ist mit den Navier-Stokes-Gleichungen die Impulsgleichung[1] für Strömungen gemeint. Im erweiterten Sinne,[2] insbesondere in der numerischen Strömungsmechanik, wird diese Impulsgleichung um die Kontinuitätsgleichung und die Energiegleichung erweitert. Sie bildet dann ein System von nichtlinearen partiellen Differentialgleichungen zweiter Ordnung.
Der daraus resultierende Formalismus ist das grundlegende mathematische Modell der Strömungsmechanik. Insbesondere lassen sich mit diesen Gleichungen Turbulenzen und Grenzschichten beschreiben.
Die Navier-Stokes-Gleichungen bilden das Verhalten von Wasser, Luft und Ölen ab und werden daher in vereinfachter Form bei der Entwicklung von Fahrzeugen wie Autos und Flugzeugen angewendet. Dies geschieht in Näherungsform, da keine exakten analytischen Lösungen für diese komplizierten Anwendungsfälle bekannt sind. Die Existenz und Eindeutigkeit einer Lösung der Gleichungen ist für den allgemeinen Fall noch nicht nachgewiesen.
Einen wesentlichen Fortschritt im theoretischen und praktischen Verständnis viskoser Fluide lieferte Ludwig Prandtl 1904 mit seiner Grenzschichttheorie. Ab Mitte des 20. Jahrhunderts entwickelte sich die numerische Strömungsmechanik so weit, dass mit ihrer Hilfe für praktische Probleme Lösungen der Navier-Stokes-Gleichungen gefunden werden können, die gut mit den realen Strömungsvorgängen übereinstimmen.[3]
Wie bereits erwähnt, bilden die Navier-Stokes-Gleichungen im engeren Sinne den Impulssatz als Anwendung der Newtonschen Axiome auf ein Kontinuum ab. Eine allgemein verwendete Form für kompressible Fluide lautet:[4]
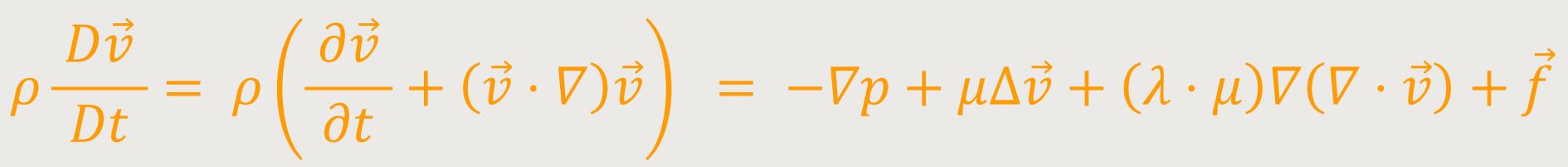
Hier ist ρ die Dichte, p der (statische)
Druck, 
die Geschwindigkeit
eines Teilchens in der Strömung, der Überpunkt genauso wie
D/Dt unten ist die substantielle Ableitung nach der Zeit,
∂/∂t die partielle Ableitung nach der Zeit bei festgehaltenem
Ort des Fluidelements, „·” das
(formale) Skalarprodukt mit dem Nabla-Operator ∇ und
Δ der Laplace-Operator.
Auf der linken Seite der Gleichung steht die substantielle Beschleunigung der
Fluidelemente. Der mit dem Nabla-Operator gebildete Term stellt ihren konvektiven
Anteil dar. Der Vektor 
steht für
eine Volumenkraftdichte wie beispielsweise die Gravitation oder die
Corioliskraft, jeweils bezogen auf das Einheitsvolumen, und besitzt die
Eine andere Schreibweise obiger Gleichung lautet:[5]
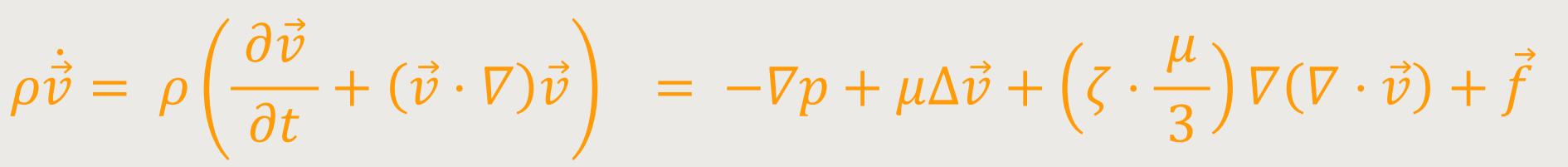
Darin ist ζ die Volumenviskosität. Mit der
Kontinuitätsgleichung und Anwendung der Stokesschen Hypothese
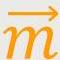= p:
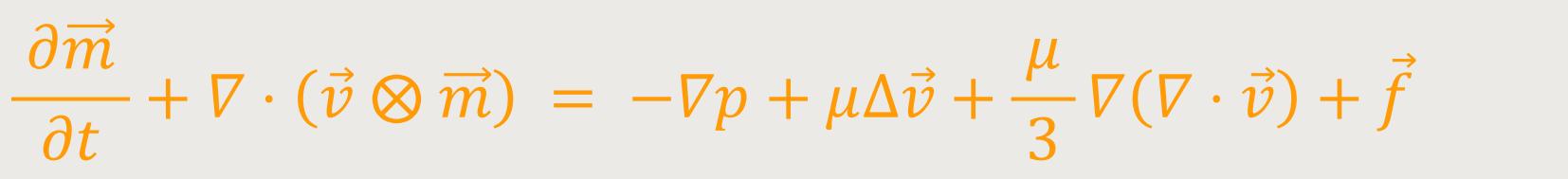
Das Rechenzeichen ⨂ bildet das dyadische Produkt. Das dyadische Produkt oder auch tensorielles Produkt genannt, ist in der Mathematik ein spezielles Produkt zweier Vektoren.
Um weitere Parameter zu berücksichtigen, müssen in die Gleichungen noch die Massenbilanz oder Kontinuitätsgleichung (Massenerhaltungssatz) und bei Gasen die Energiebilanz (Energieerhaltungssatz) hinzugefügt werden. Je nachdem, welche weiteren Anforderungen an das Fluid gestellt werden, ergibt sich das vollständige System in unterschiedlicher Form.
Die am häufigsten verwendete Form sind die Navier-Stokes-Gleichungen für inkompressible Fluide. Denn sie sind für Unterschallströmungen gut geeignet und ihre Berechnung ist einfacher als die kompressibler Fluide. Wir beschränken uns in diesem Kapitel nur auf kompressible Fluide.
Die Vektorform der Gleichungen gilt in jedem Koordinatensystem. Nachfolgend werden die Komponentengleichungen der Impulsgleichung speziell für kartesische Koordinaten angegeben.[7]
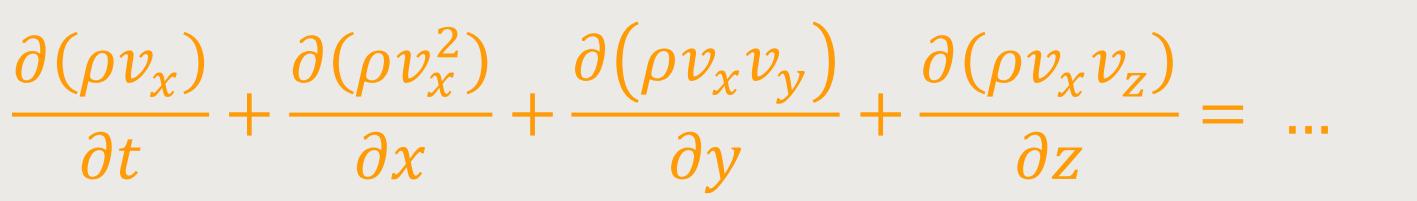
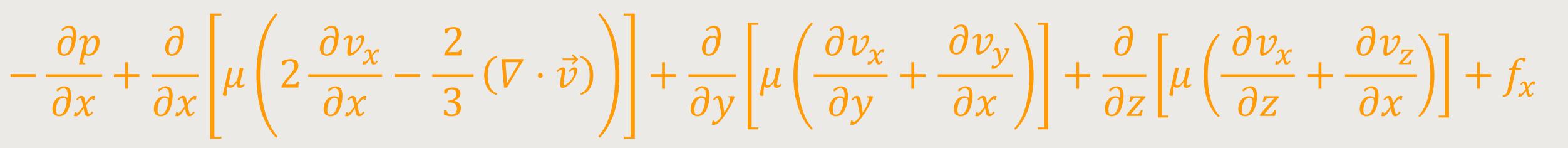
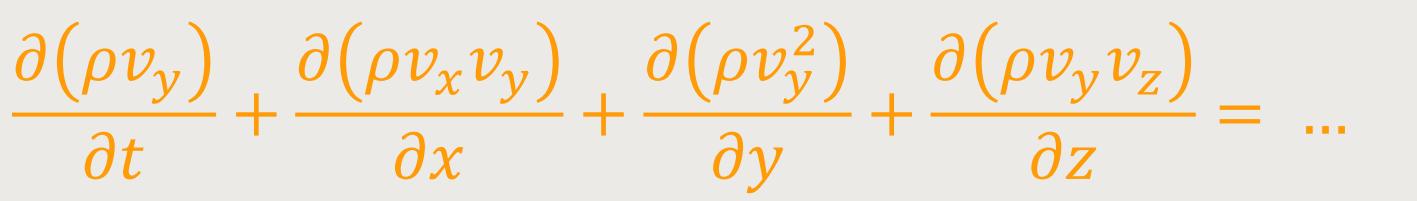
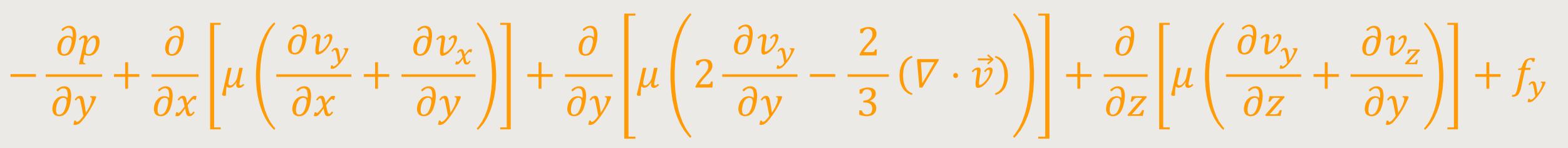
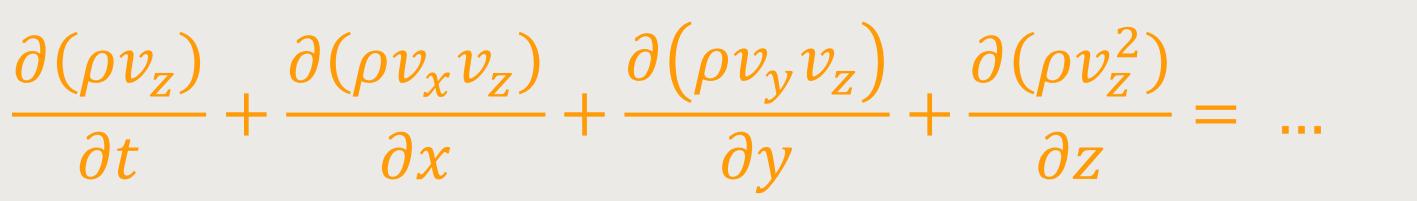
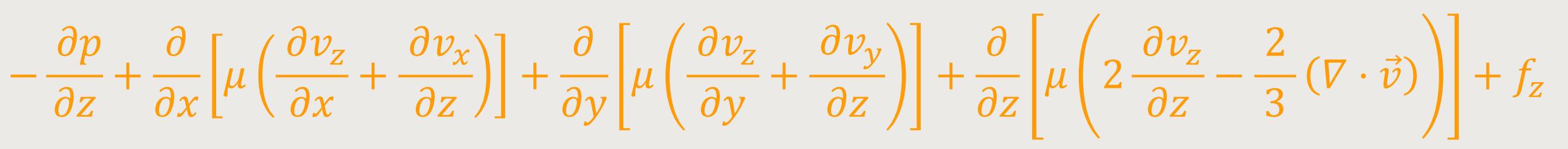
Darin sind v(x,y,z) und ƒ(x,y,z)
die Vektorkomponenten in den räumlichen
Die Navier-Stokes-Gleichungen können mit charakteristischen Maßen des gesamten Strömungsgebiets für die Länge L, die Geschwindigkeit v∞ und die Dichte ρ∞ dimensionslos dargestellt werden. Damit entstehen folgende dimensionslose Größen:
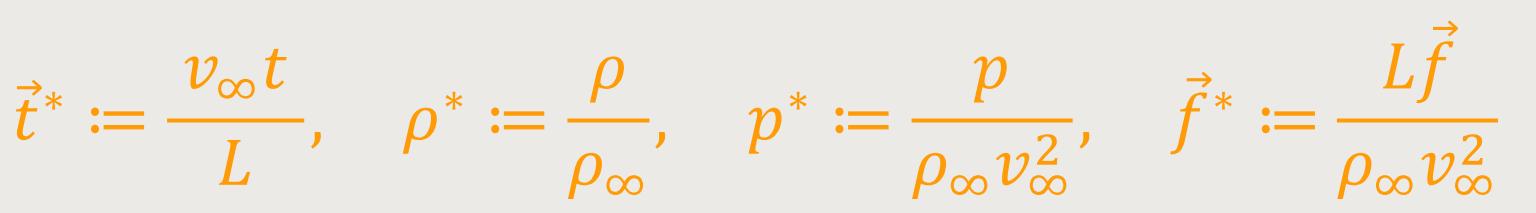
Dies führt zu der dimensionslosen Impulsgleichung:
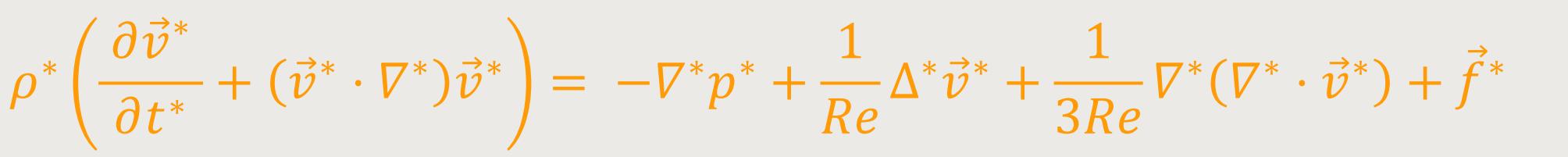
Darin charakterisiert die dimensionslose Reynolds-Zahl ...
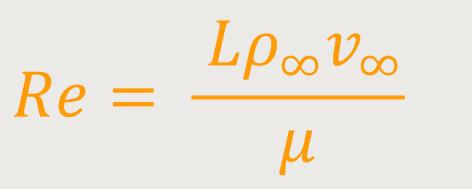
... die Strömung hinsichtlich des Verhältnisses von Trägheits-
zu Scherkräften.[8] Bei Strömungen mit freier
Oberfläche enthält die dimensionslose Kraftdichte
∗
Für kompressible Gase werden die obigen Impulsgleichungen um die Energiebilanz und die Zustandsgleichung eines idealen Gases erweitert. Der komplette Satz an Gleichungen besteht also aus der Kontinuitätsgleichung (Massenerhaltung), Impulsbilanz (Impulserhaltung), Energiebilanz (Energieerhaltung) und einer Zustandsgleichung.
Unter der Annahme, dass die Dichte entlang der Teilchenbahnen konstant ist, entstehen wieder die Gleichungen für inkompressible Fluide.
Im Folgenden bedeutet ∂t die Ableitung einer
Größe nach der Zeit und ∇ ist der Nabla-Operator,
der die Ableitung nach dem Ort bildet, also je nach Verknüpfung die Divergenz oder den
Gradient, und
Die Kontinuitätsgleichung entspricht der Massenerhaltung und wird hier
mit der Impulsdichte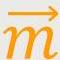
= ρ
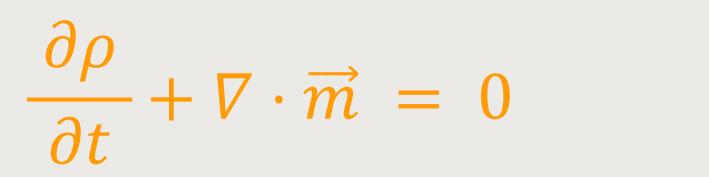
Die Impulsbilanz entspricht der Impulserhaltung und lautet in Indexschreibweise:
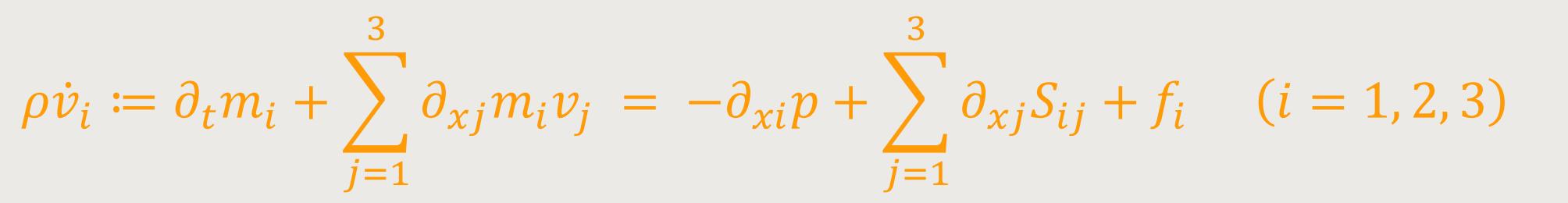
Wobei δij das Kronecker-Delta und ...
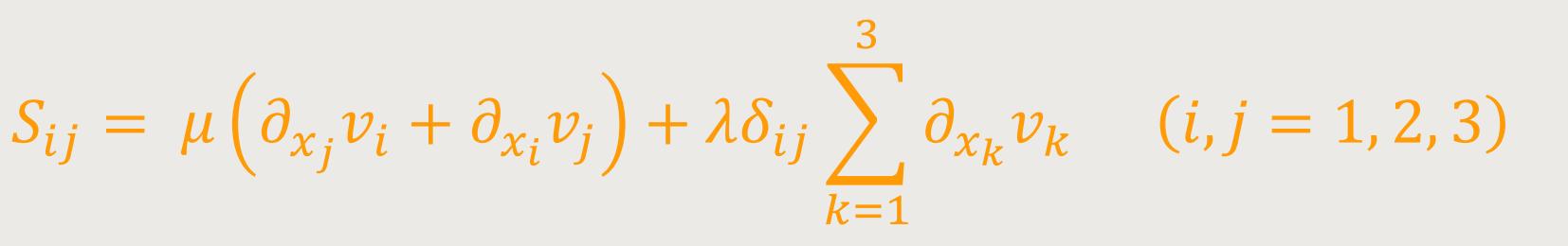
... der Reibtensor oder viskose Spannungstensor sind. Der Materialparameter
μ ist die dynamische Viskosität, λ
die erste Lamé-Konstante (Materialkonstante) und ƒi
ist die
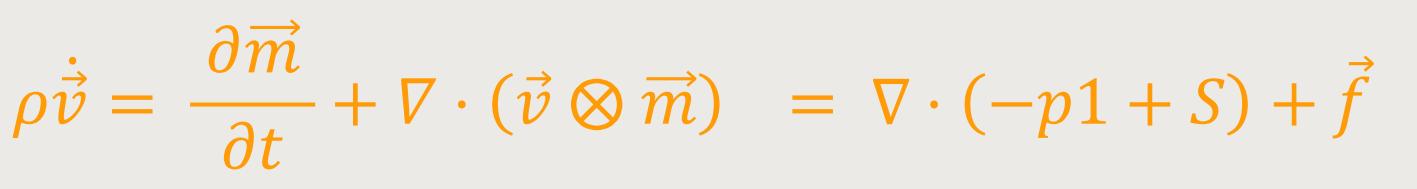
Wobei ...
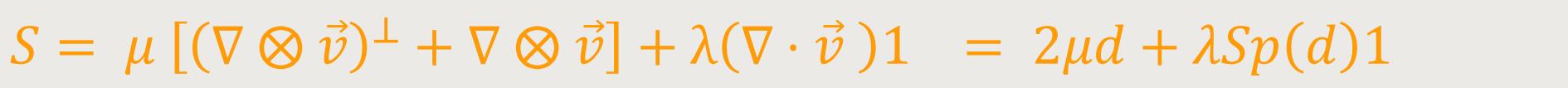
... der viskose Spannungstensor, d der
Verzerrungsgeschwindigkeitstensor, welcher der symmetrische Anteil des
Geschwindigkeitsgradienten
⊤
Die Energiebilanz am Fluidteilchen im Schwerefeld der Erde lautet:
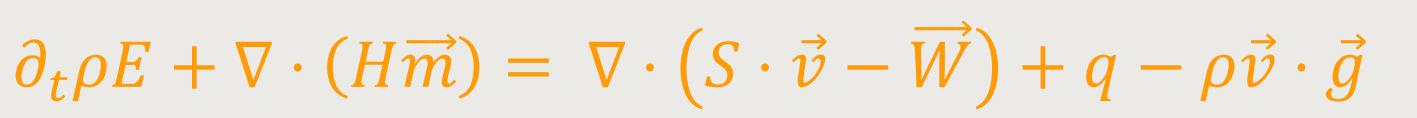
Wobei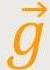 
die Schwerebeschleunigung
und ...
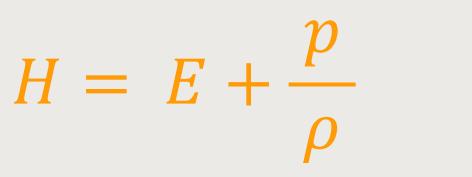
... die Enthalpie pro Einheitsmasse ist. Das negative Vorzeichen vor der
Schwerebeschleunigung resultiert aus dem abwärts gerichteten Vektor
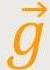, sodass in einer aufwärts
führenden Strömung potentielle Energie hinzu gewonnen wird. Der
Wärmefluss mittels 
kann
mittels des Wärmeleitkoeffizienten κ als ...
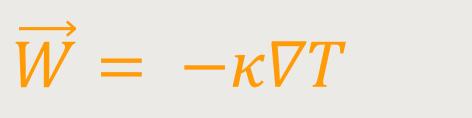
... geschrieben werden. Mit dem Quellterm q kann beispielsweise die Absorption und Emission von Wärme aus Treibhausgasen infolge von Einstrahlung beschrieben werden. Die totale Energie pro Einheitsmasse E ist die Summe von innerer (e) kinetischer und potentieller Energie, sie lässt sich (mit der Höhe h) also schreiben als:
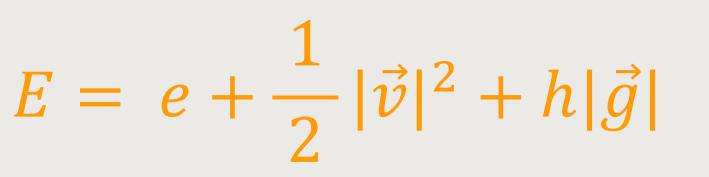
Nun liegen also vier Gleichungen für fünf Variablen vor und das System wird durch die folgende Zustandsgleichung abgeschlossen:
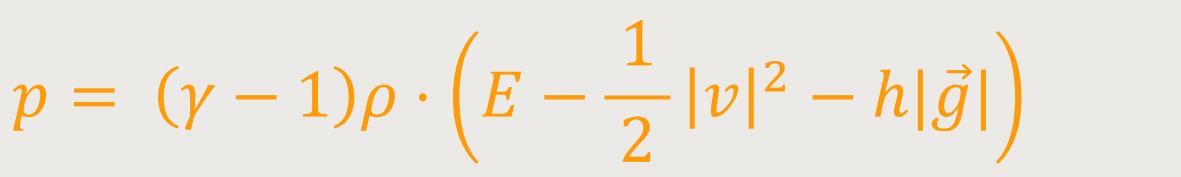
Die thermodynamischen Größen Dichte, Druck und Temperatur sind durch das ideale Gasgesetz verbunden:
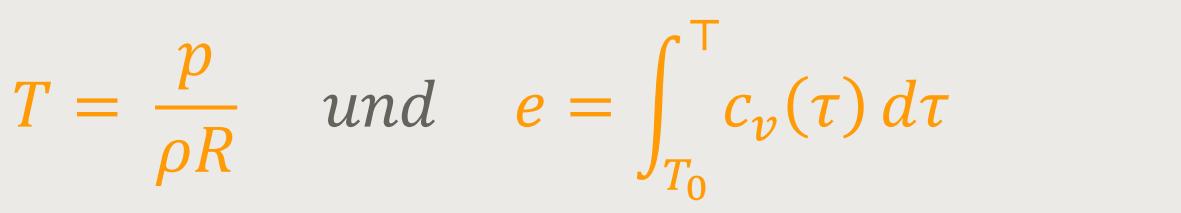
Oft geht man zusätzlich von einem perfekten Gas mit konstanter spezifischer Wärmekapazität cv aus. Dann vereinfacht sich das Integral und es gilt:
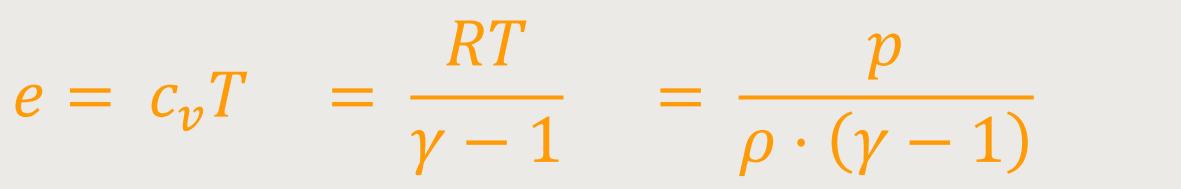
In beiden Fällen hängen der Isentropenexponent γ
und die Gaskonstante R durch den spezifischen Wärmekoeffizienten
für konstanten Druck cp respektive konstantes Volumen
cv durch
Ein wesentlicher Punkt bei den Navier-Stokes-Gleichungen ist die experimentell sehr gut nachgewiesene Haftbedingung (No-Slip-Bedingung), bei der an einer Wand sowohl in Normalenrichtung als auch insbesondere in tangentialer Richtung als Relativgeschwindigkeit Null vorgeschrieben werden. Die Fluidteilchen kleben also an der Wand. Dies führt zur Bildung einer Grenzschicht, die für wesentliche, nur durch die Navier-Stokes-Gleichungen modellierte Phänomene verantwortlich ist. Nur wenn die freie Weglänge bewegter Moleküle groß ist zur charakteristischen Länge der Geometrie (z. B. für Gase mit extrem niedrigen Dichten oder Strömungen in extrem engen Spalten) ist diese Bedingung nicht mehr sinnvoll.
Durch dynamische (also Kraft-) Randbedingungen auf einer Fläche wird die
Fläche im Allgemeinen deformiert und die Strömung folgt ihr. Zum Problem
gehört dann die Bestimmung der Fläche dazu. Sie ergibt sich aus der Vorgabe des
Flächenkraft- oder Spannungsvektors 
der Normaleneinheitsvektor der
Fläche ist und sich der Spannungstensor aus der Materialgleichung
Bei entsprechend kleinskaligen Strömungen ist die Oberflächenspannung zu berücksichtigen, die nach der Young-Laplace-Gleichung von der Krümmung der Oberfläche abhängt. Bei schwacher Krümmung entsteht für den Druck an der Oberfläche die Gleichung
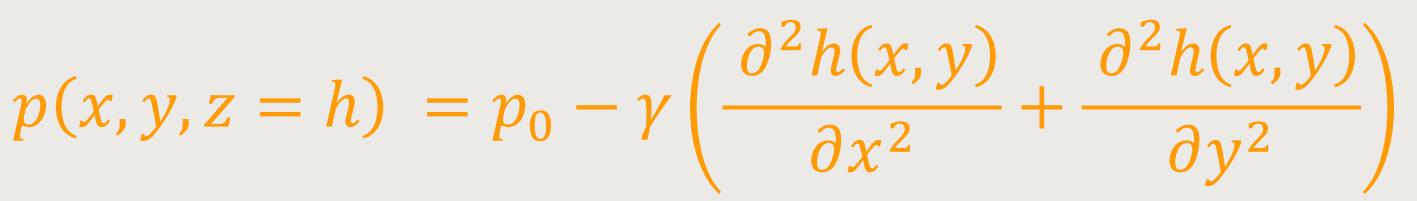
Hier ist p₀ der vorgegebene Druck auf der Fläche h, die hier die Flächenparameter x und y besitzt, und γ ist ein Parameter, der die Stärke der Oberflächenspannung skaliert.[11]
Zusätzlich muss gegebenenfalls am Rand noch entweder eine Temperatur oder ein Wärmefluss vorgeschrieben werden.
Quellen
[1] L.D. Landau, E.M. Lifshitz: Fluid Mechanics - Course of Theoretical Physics, Institute of Physical Problems, Pergamon Press, 1966, S. 47-53.[2] A. Chorin, J.-E. Marsden: A Mathematical Introduction to Fluid Mechanics. Springer Verlag, 2000.
[3] F. Durst: Grundlagen der Strömungsmechanik. Springer, 2006, S. 10-16.
[4] J.-N. Reddy: An Introduction to Continuum Mechanics. Cambridge 2008, S. 212-214.
[5] L.D. Landau, E.M. Lifshitz: Fluid Mechanics - Course of Theoretical Physics, Institute of Physical Problems, Pergamon Press, 1966, S. 47-53.
[6] G. G. Stokes: On the Theories of Internal Friction of Fluids in Motion. In: Transactions of the Cambridge Philosophical Society. Band 8, 1845, S. 287-305.
[7] Oertel (2012), S. 252.
[8] Oertel (2012), S. 267 ff.
[9] L. D. Landau, E. M. Lifshitz: Fluid Mechanics - Course of Theoretical Physics, Volume 6, Institute of Physical Problems, Pergamon Press, 1966.
[10] P. Haupt: Continuum Mechanics and Theory of Materials. Springer, 2002, S. 182 ff.
[11] M. Bestehorn: Hydrodynamik und Strukturbildung. Springer, 2006, S. 64.
Der Text auf dieser Seite basiert auf dem Artikel Navier-Stokes-Gleichungen aus der freien Enzyklopädie Wikipedia und ist unter der Lizenz Creative Commons Attribution-ShareAlike 3.0 Unported - Deed verfügbar.
⇦ Kapitel Kapitel ⇨