Eine Spirale, auch Schnecken­linie genannt, ist eine Kurve, die um einen Punkt oder eine Achse verläuft und sich je nach Perspektive des Betrachters von diesem Zentrum entfernt oder sich ihm annähert. Zum Beispiel gleicht die Kalk­schale der Ammoniten einer logarith­mischen Spirale.

Abb. 1: Die Kalkschale der Ammoniten gleicht einer logarithmischen Spirale (CC BY-SA 3.0)

Spiralen werden oft zur Konstruktion von krümmungs­stetigen Übergangs­kurven verwendet.

Die Spirale wird manchmal mit der Schraube verwechselt. Während die proto­typische Spirale ein Gebilde in der Ebene ist, wie zum Beispiel die Rille einer Schall­platte, ist sowohl die Schraube als auch der Wendel­bohrer ein räum­liches Gebilde entlang des Hofes eines Zylinders. Die Schrauben­linie oder zylindrische Spirale bzw. Wendel wird auch als Helix bezeichnet. Bei ihr handelt es sich um eine Kurve, die sich mit konstanter Steigung um den Mantel eines Zylinders windet. Insofern eignen sich Schrauben sehr gut, um Bauteile mitein­ander zu verbinden. Aber bei unserer Betrachtung geht es um andere Kurven­verläufe.

Man kann Spiralen mathe­matisch am besten als Koordinaten­gleichungen im ebenen Polar­koordinaten­system beschreiben. Der Radius r wird dabei als Funktion r(φ) von φ darge­stellt. Der Winkel φ läuft im Allge­meinen bis unend­lich, anstatt nur einen Umlauf bis 2π. Auch negative Winkel sind möglich.

Die Polardarstellung einer Spirale ist definiert als:

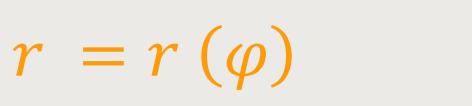
In x-y-Koordinaten werden dadurch die Punkte mit folgender Parameter­darstellung beschrieben:

Ersetzt man in der Polardar­stellung φ durch φ − φ₀ , so wird die Spirale um den Winkel φ₀ gedreht.

Im Nach­folgenden werden wir einige der wichtigsten Ebenen Spiralen betrachten. Bei der Gegen­über­stellung geht es unter anderem um die Frage, welche dieser Spiralen eignet sich womög­lich, um den Wachstums­mechanismus in der Natur wieder­zugeben.

Die Archi­medische Spirale, auch arith­metische Spirale genannt, ist die einfachste, quasi die Mutter aller Spiralen. Sie entsteht, wenn bei einer Dreh­bewegung der Radius r propor­tional zum Dreh­winkel φ wächst.

Die Polar­darstellung der Archi­medischen Spirale ist definiert als:

Abb. 2: Archimedische Spirale (rechtsdrehend)

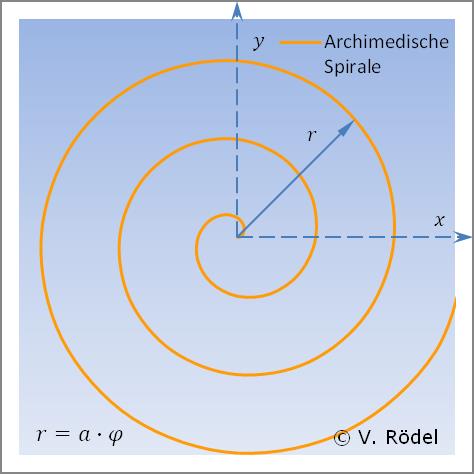
Die Archime­dische Spirale entsteht z.B. beim Aufwickeln eines Teppichs mit gleich­mäßiger Dicke. Sie wird in der r-φ-Ebene durch eine Gerade beschrieben.

Die Darstellung als Parameter­darstellung in karte­sischen Koordinaten lautet:

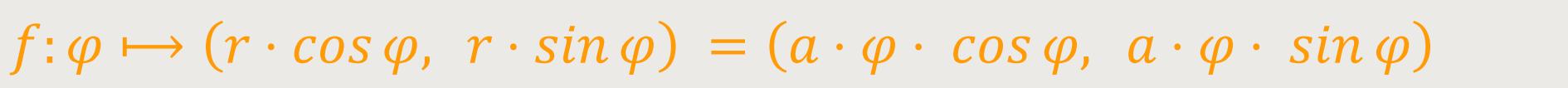
Die Länge eines Bogen­stückes von φ₁ bis φ₂ ist:

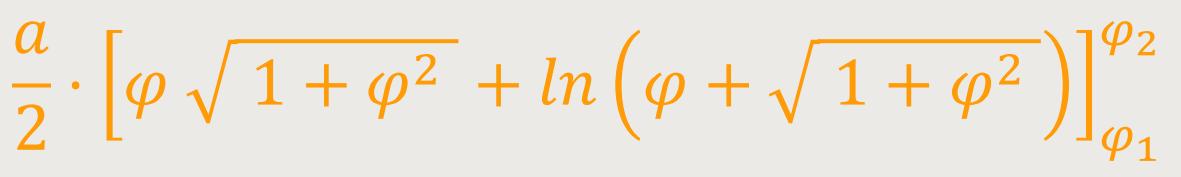
oder in Kurzschreibweise:

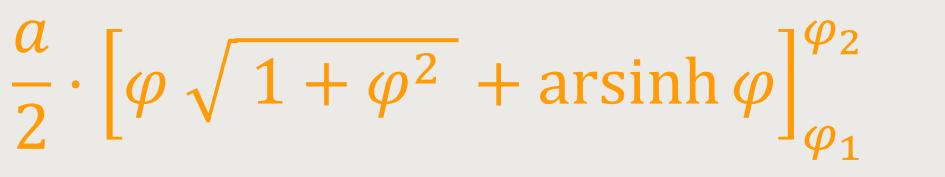
Die Gesamt­länge der Spirale von φ₁ = 0 bis φ₂ = φ ist demnach:

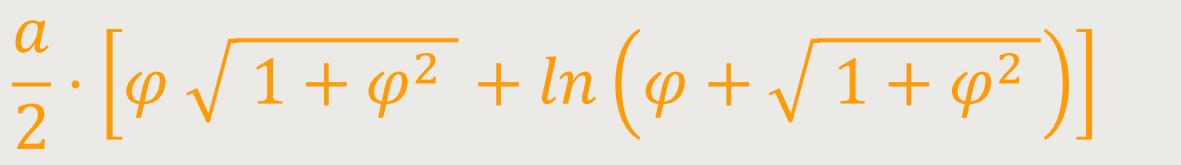
Die Fläche, die bei der ersten Umdrehung einge­schlossen wird, beträgt:

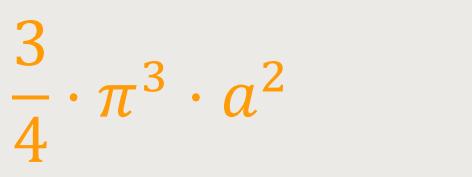
Wogegen bei der n-ten Umdrehung die Fläche zusätz­lich einge­schlossen wird:

Die Krümmung k berechnet sich in Abhängig­keit vom Dreh­winkel φ. Wenn man beispiels­weise bei der Archi­medischen Spirale für n = 1 setzt, erhält man die Krümmung:

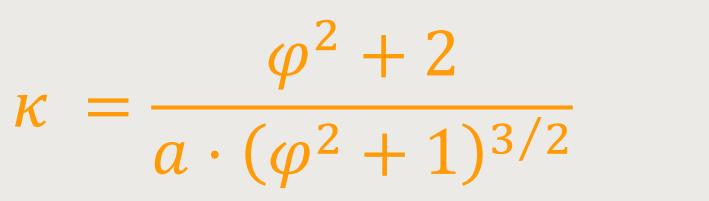
Neben der Darstellung als Parameter­darstellung lässt sich die Archime­dische Spirale auch als Gleichung beschreiben:

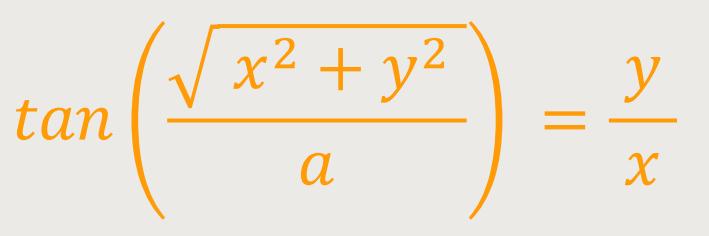
Jeder vom Koordinaten­ursprung (0|0) ausgehende Strahl schneidet aufein­ander folgende Windungen der Archime­dischen Spirale r = a · φ in Punkten mit dem konstanten Abstand a · 2π. Daher kommt auch die Alternativ-Bezeichnung „Arith­metische Spirale”.

Es gibt verschiedene Verall­gemeinerungen der ursprüng­lich von Archimedes beschrie­benen Spirale, für die in der Literatur auch oft „Archime­dische Spiralen” als Sammel­begriff verwendet werden.

Hierbei wird die ursprüng­liche Gleichung r = a · φ zu r = b + a · φ^1/d erweitert. Für d = 1, b = 0 erhält man die gewöhnliche Spirale des Archimedes. Der Fall d = 2, b = 0 wird auch als Fermatsche Spirale bezeichnet und der Fall d = −2, b = 0 als Lituus-Spirale.

Generell können sich diese Spiralen in Eigen­schaften und Aussehen deutlich von der ursprüng­lichen Archime­dischen Spirale unter­scheiden.

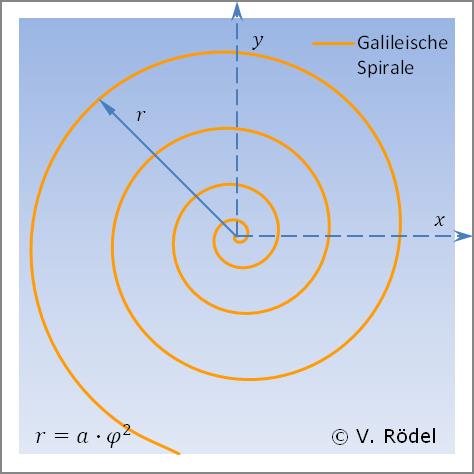
Die Galileische Spirale ist eine Spirale, bei der sich mit jeder Umdrehung um ihren Mittel­punkt oder ihre Achse der Abstand von diesem Mittel­punkt um den gleichen Faktor verän­dert. Der Radius wächst propor­tional zur Bogen- bzw. Spiral­länge.

Wie die zuvor behandelte Spirale ist auch die Galileische Spirale eine ebene Kurve, die sich in Polar­koordinaten beschreiben lässt, wobei die Gleichung eine Funktion des Radius beschreibt.

Die Polar­darstellung der Galileischen Spirale ist definiert als:

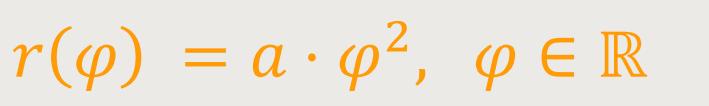
Die Spirale lässt sich in karte­sischen Koordinaten (x = r · cos φ,   y = r · sin φ) durch die Parameter­darstellung beschreiben.

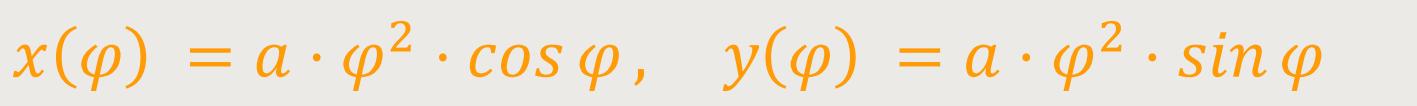
Der Parameter r wird gebildet aus

Nur relativ flache Spiralen mit einer Steigung von a « 1 ergeben reizvolle Schnecken. In nachfolgender Grafik beträgt die Steigung a = 0,000018.

Abb. 3: Galileische Spirale (rechtsdrehend)

Die Krümmung einer Galileischen Spirale für r = a · φ² ist:

Für eine Spirale mit der Gleichung

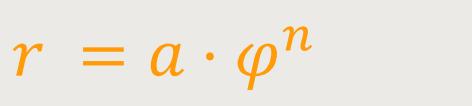
ist die polare Steigung:

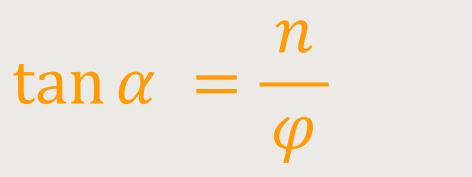
Für die Galileische Spirale ist n = 2 und damit tan α = 2/φ.

Die Logarith­mische Spirale ist eine Spirale, bei der sich mit jeder Umdrehung um ihren Mittel­punkt oder ihre Achse der Abstand von diesem Mittel­punkt um den gleichen Faktor verändert. Der Radius wächst somit propor­tional zur Bogen- bzw. Spiral­länge. Da jede Gerade, die durch den Pol verläuft, die Logarith­mische Spirale stets unter dem gleichen Winkel schneidet, spricht man auch von einer „gleich­winkligen Spirale”.

Wie die zuvor behandelten Spiralen ist auch die Logarith­mische Spirale eine ebene Kurve, die sich in Polar­koordinaten beschreiben lässt, wobei die Gleichung eine Funktion des Radius beschreibt.

Die Polar­darstellung der Logarith­mischen Spirale ist definiert als:

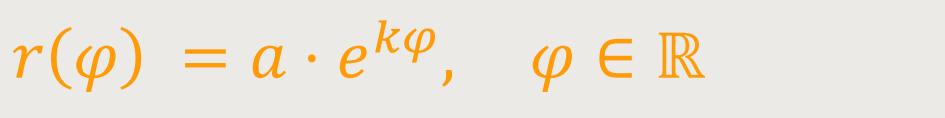
k ist die Steigung der Spirale

Die Steigung k kann auch durch tan α ausge­drückt werden, wobei α dann der Steigungs­winkel ist. Nicht zu verwechseln mit dem Tangenten­winkel.

Die Spirale lässt sich in karte­sischen Koordinaten (x = r · cos φ,   y = r · sin φ) durch die Parameter­darstellung beschreiben:

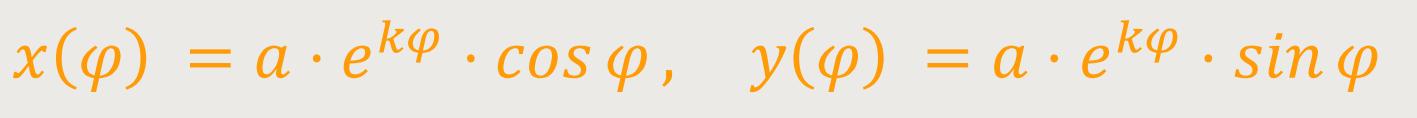
Entsprechend ihrer Namens­gebung kann der Winkel als Funktion des Radius r ausge­drückt werden:

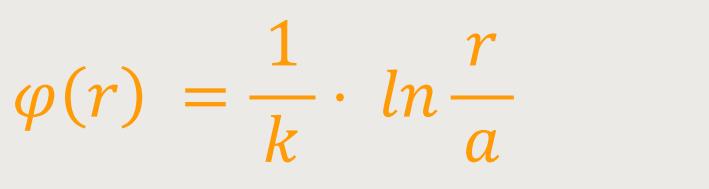
Der Parameter r wird gebildet aus:

Bei der Logarith­mischen Spirale gibt es eine Reihe auffallender Eigen­schaften. Zum Beispiel gibt das Vorzeichen von a · k die Dreh­richtung in der Ebene wieder.

Die Spirale umkreist den Ursprung unend­lich oft, ohne ihn zu erreichen. Man bezeichnet dies auch als asympto­tischen Punkt.

Dagegen ist die Bogen­länge von jedem Kurven­punkt bis zum Pol endlich und beträgt:

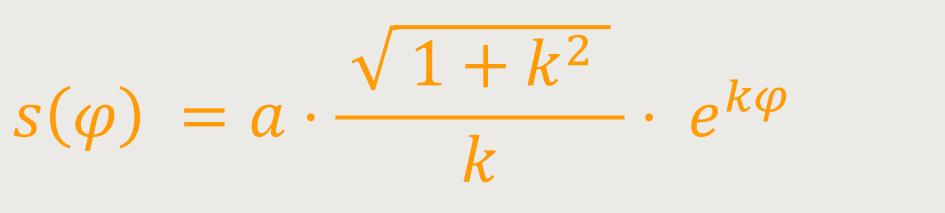
Mit jeder Windung wächst der Radius um einen konstanten Faktor:

Nur relativ flache Spiralen mit einer Steigung von k ≪ 1 ergeben reiz­volle Schnecken. In nach­folgender Grafik beträgt die Steigung a = 1,15 und die Krümmung k = 0,014.

Abb. 4: Logarithmische Spirale (rechtsdrehend)

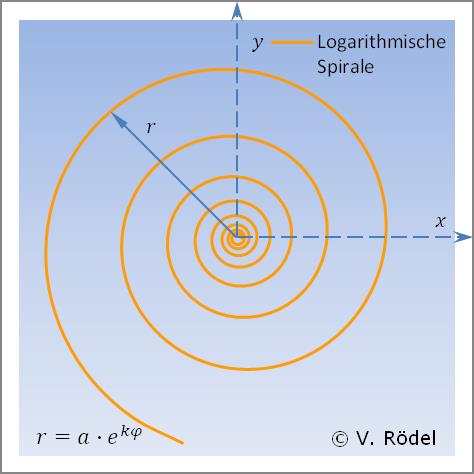
Die Logarith­mische Spirale entsteht zum Beispiel beim Wachstum von Schnecken­häusern. Ihr Name rührt von der Auflösung ihrer Polar­gleichung nach φ her.

Die Krümmung einer Logarith­mischen Spirale für r = a · e ^kφ ist:

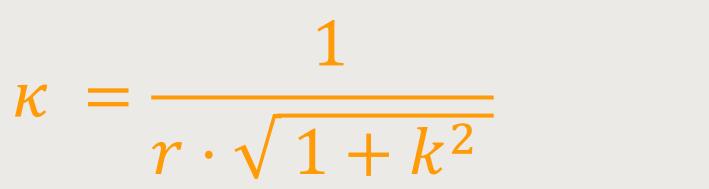
Der Winkel α, unter dem die Spiral­tangente den zuge­hörigen Polar­kreis schneidet, heißt polarer Steigungs­winkel und tan α die polare Steigung. Aus der Formel für den Tangenten­vektor ergibt sich:

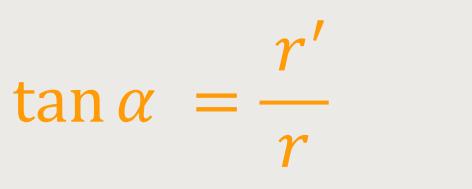
Für eine Spirale mit der Gleichung

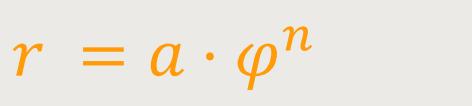
ist die polare Steigung:

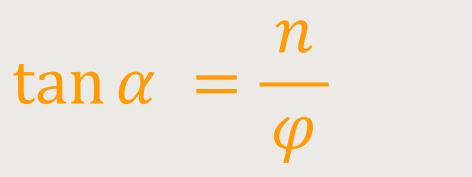
Für die Archi­medische Spirale ist n = 1 und damit tan α = 1/φ.

Für die Logarith­mische Spirale ist tan α = k konstant.

Das grafische Ergebnis einer Logarith­mischen Spirale lässt sich auch ohne die Eulerzahl e nur auf Basis der Steigung k oder mittels der Maßzahl Φ (Phi) des Goldenen Schnitts darstellen.

In der nach­folgenden Grafik wurde alter­nativ in einem Fall die „Steigung” und im anderen Fall die „Krümmung” gering­fügig verändert, um den visuellen Effekt zu verdeut­lichen. Aber letztlich wären alle drei Vorgehens­weisen völlig deckungs­gleich.

Abb. 5: Ein Vergleich verschiedener Herangehensweisen

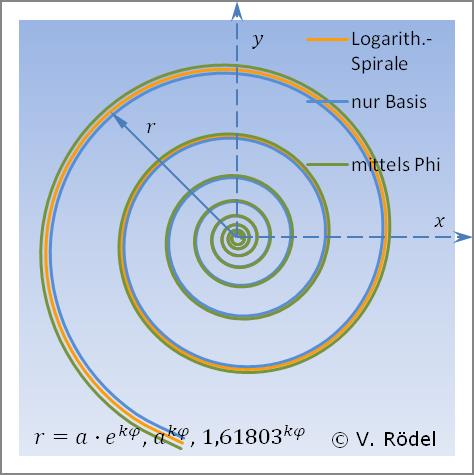
Das ist ein klassisches Beispiel dafür, dass sich die Natur auf verschiedene Art und Weise darstellen lässt.

Bevor wir einen Schritt weiter gehen, möchten wir die Ebenen Spiralen noch um einige „Varianten” erweitern.

⇦ Kapitel Kapitel ⇨