Die Idee von einem 4-dimen­sionalen gekrümm­ten Raum trat erst­mals mit Albert Einsteins Relativitäts­theorie (ART) ins Bewusst­sein der Menschen. Die ART führt die Gravita­tion auf eine Krüm­mung von Raum und Zeit zurück, die unter anderem durch die beteiligten Massen verursacht wird.

Ein Raum mit vier Dimen­sionen scheint sich zunächst unserem Vorstellungs­vermögen zu ent­ziehen. Dabei ist es gar nicht so kompli­ziert, sich einen solchen Raum vorzu­stellen und entspre­chend zu visuali­sieren. Wir wollen uns zunächst zwei Situationen vorstellen.

Im ersten Fall geht es um einen Zylinder, ähnlich einer Toiletten­rolle, der auf­recht auf seiner Grund­fläche steht. Sein Volumen wird bestimmt durch die Grund­fläche multi­pliziert mit seiner Höhe. Oder als Formel aus­gedrückt:

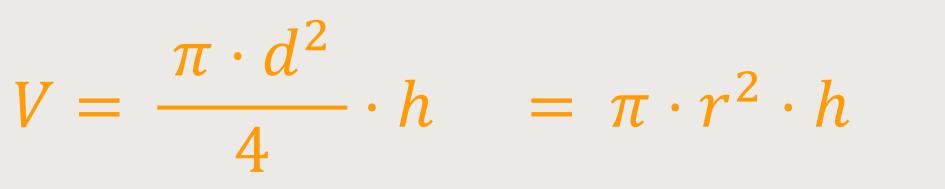
Nun schauen wir uns dieses Volumen etwas näher an. Dazu teilen wir den Zylinder von oben nach unten in viele kleine Scheiben. Die Scheiben sollen am Ende so flach sein, dass deren Höhe dann nur noch der Dimen­sion eines Wasserstoff­moleküls entspricht. Im weiteren Verlauf wird der Einfach­heit halber nur noch von einer Teilchen­scheibe gesprochen.

Wie viele solcher Teilchen letztlich neben­einander auf eine derartige Scheibe passen, hängt natür­lich von den Abmaßen der gewählten Fläche ab, aber auch von den Bindungs­kräften und dem Druck, die in dem Volumen wirken. Aber letzteres bleibt bei unserer Betrach­tung vorerst unberück­sichtigt.

Jetzt stellen wir uns weiter vor, der Zylinder wäre unendlich lang und die Moleküle würden sich in dem System in eine Rich­tung aus­breiten. Würde man hierzu ein Koordinaten­system be­rück­sichtigen, wäre die Teilchen­scheibe selbst durch die x-y-Koordinaten bestimmt, wogegen die Höhe bzw. die Länge des Systems durch die z-Achse definiert wird. Diese z-Achse, oder in unserem Fall die Zylinder­achse, läuft mittig durch den Koordinaten­ursprung. Demnach sollen sich alle Moleküle in Richtung der positiven z-Achse fort­bewegen. Das ist zu­nächst alles unspekta­kulär und ent­spricht in der Physik dem klas­sischen Spezial­fall. Man spricht dabei auch gerne von einem „Inertial­system”.

In der Physik versteht man unter einem solchen Inertial­system ein Bezugs­system, in welchem jeder kräfte­freie Körper relativ zu diesem Bezugs­system in Ruhe verharrt oder sich gleich­förmig und gerad­linig bewegt. Kräfte­frei bedeutet, dass der Körper keine Kräfte von anderen Objekten erfährt oder diese sich insgesamt aufheben, sodass die resultie­rende Kraft Null ist.

Bei genauer Betrachtung wird deutlich, dass die z-Achse der Zeit t ent­spricht. Denn bei verstreichen einer bestimmten Zeit legen die Moleküle in Richtung der positiven z-Achse eine gewisse Strecke zurück. In diesem Fall verläuft die Zeit parallel zur z-Achse. Oder anders ausge­drückt, die z-Achse und die t-Achse ver­schmelzen mit­einander. Aus diesem Grund hat es für uns den Anschein, als würden wir aus­schließ­lich in einem 3-dimen­sionalen Raum leben. Das trifft aber nur dann zu, wenn wir kleine Abschnitte betrachten. Im Verhältnis zu den Dimen­sionen des Universums sehen wir Menschen unsere Umwelt in sehr, sehr kleinen Abschnitten.

In verein­fachter Form befinden wir uns, bezogen auf die Moleküle, bereits in einem 4-dimensionalen Raum. Denn das Molekül selbst wird durch die drei Raum­koordinaten x-y-z bestimmt und bewegt sich in der Zeit t auf einer in allen Raum­richtungen gekrümmten Bahn.

An unserer bis­herigen Betrach­tung wird deut­lich, dass man streng­genommen immer dann von einem 4-dimen­sionalen Raum sprechen kann, wenn sich das System in Bewegung befindet. Und genau das ent­spricht unserer Realität. Alles um uns herum unter­liegt einem stetigen Fluss. Selbst vermeint­lich starre Körper verändern ihre Struktur auf mole­kularer Ebene. Die Frequenzen bzw. die Schwin­gungen der Elementar­teilchen ent­scheiden darüber, wie viel Masse es besitzt. Unter Berück­sichtigung der inneren Bindungs­kräfte, hat das letzt­lich sogar Ein­fluss darauf, ob wir einen Körper als vermeint­lich fest ansehen, oder ob er uns wie Wasser durch die Hände rinnt.

Wird dagegen eine konstante Kraft auf das System ausgeübt, wird sich der Körper, oder hier ist es ein Gas beste­hend aus Wasserstoff­molekülen, trans­versal in eine Richtung fort­bewegen. Als Ergebnis haben wir zwar ein System in Bewegung, aber der Aspekt des 4-dimen­sionalen Raumes ist dennoch nur bedingt erfüllt. Daran wird deut­lich, dass die vierte Dimension nicht allein durch das Hinzu­fügen der Zeit definiert ist. Viel­mehr spielt hierbei auch die Krümmung des Raumes eine wesent­liche Rolle.

Wie lässt sich aber der 4-dimen­sionale Raum im Detail charakte­risieren? Dazu denken wir uns erneut einen Zylinder dessen Grund­fläche auf der x-y-Achse eines karte­sischen Koordi­naten­systems ange­ordnet ist. Der Mittel­punkt dieser Kreis­fläche fällt wieder mit dem Ursprung des Koordinaten­systems zusammen. Jetzt ergibt sich aber ein gravie­render Unter­schied zu unserem klas­sischen 3-dimen­sionalen Raum­verständnis.

Die z-Achse bleibt nur noch in Bezug auf das jeweils betrach­tete Körper­system (Bezugs­system) erhalten. Dagegen muss die t-Achse (Zeit) jetzt völlig losge­löst von der z-Achse des gesamten über­geordneten Systems betrachtet werden. Mit anderen Worten, die t-Achse verläuft allen­falls nur einmal im Ursprung 0,0 mit der z-Achse tangen­tial zusammen. Die t-Achse beschreibt im Weiteren aus­schließ­lich einen Kurven­verlauf, der sich fortan in drei Raum­richtungen durch den Raum windet.

Wie kann man sich den Kurven­verlauf der t-Achse konkret vor­stellen? Nehmen wir an, wir hätten als Betrach­tungs­objekt ein Haar­gummi oder einen O-Ring. Die Mittel­linie durch den Quer­schnitt des Haar­gummis soll dem Umfang ent­sprechen und beschreibt dann die Form eines Kreises. In der klassischen Physik würde der Umfang am Einheits­kreis 2π entsprechen. Würde man die beiden Hälften des Kreises jeweils um 90° verwinden, käme eine 8 (∞) heraus.

Aller­dings sollen in unserer Betrach­tung die verdrehten Hälften nicht plan auf­einander liegen, sondern in einem speziell definier­ten Abstand zueinander. Je nach Betrach­tungs­winkel zeichnet der Kurven­verlauf eine gestreckte oder eine ge­stauchte 8 (∞) nach (siehe Abb. 1 und 2).

Abb. 1: In der Draufsicht beschreibt der Kurvenverlauf eine „gestreckte Acht”.


Abb. 2: In der Seitenansicht beschreibt der Kurvenverlauf eine „gestauchte Acht”.

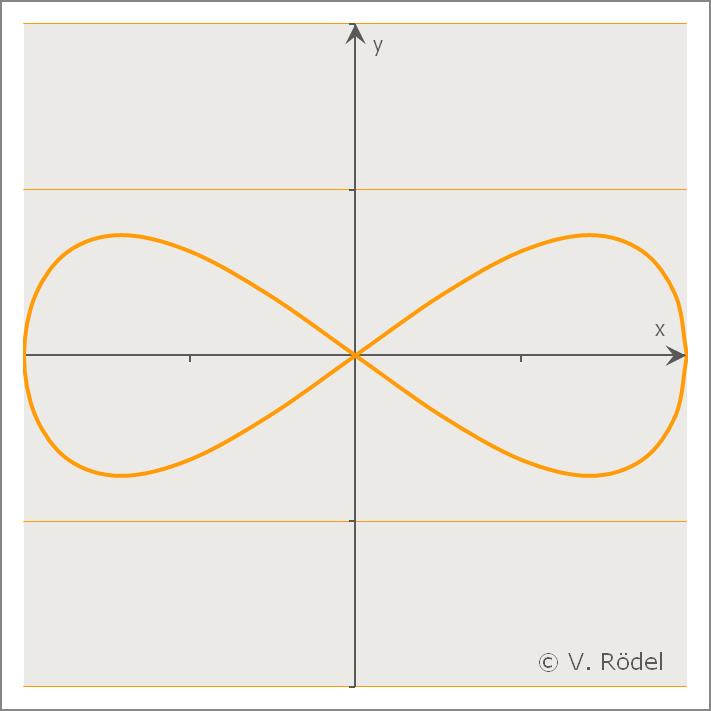
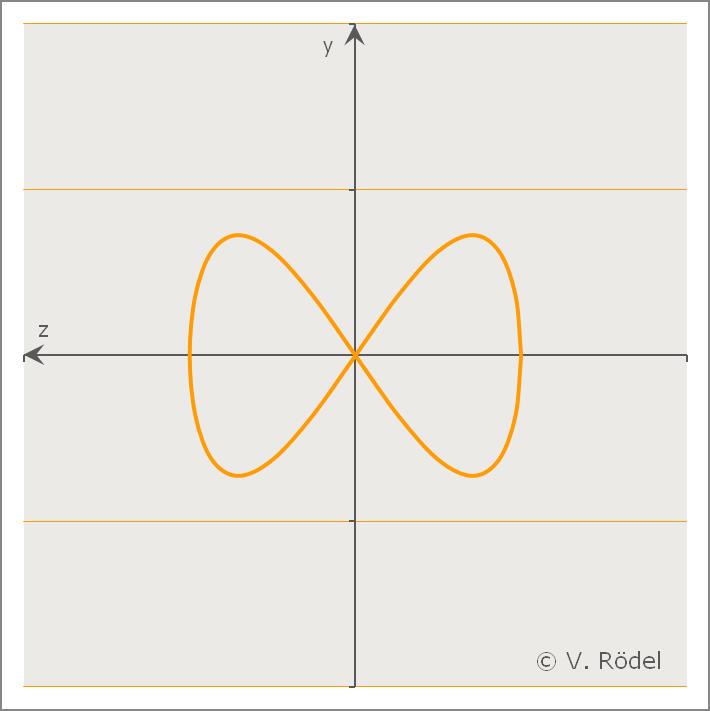
Probiert man das selbst mit einem Haar­gummi aus, wird man beim Kurven­verlauf einen gering­fügigen Unter­schied fest­stellen. Das liegt an der geschlos­senen Ring­struktur und den inneren Spannungen in dem Gummi. Um sich das gedank­lich vorzu­stellen, könnte man auf einem zunächst nicht verdrehten Haar­gummi zwei kleine ein­ander gegen­über­liegende Punkte oben auf das Haar­gummi zeichnen. Bei einer wie zuvor beschrie­benen 180°-Verdre­hung (2·90°) wandert einer dieser Punkte auf­grund der Verdre­hung auf die andere Seite. Lässt man das Haar­gummi wieder los, bildet sich wieder der Ring.

Diese inneren Spannungen würden nicht auftreten, wenn das Haar­gummi zu Beginn an einer Stelle getrennt worden wäre, anschließend der gleiche Kurven­verlauf nach­geahmt werden würde, und die beiden Enden wieder verklebt werden. In diesem Fall würde der zweite Punkt nicht um 180° versetzt liegen.

Nehmen wir an, die Spannungs­verhält­nisse im Gummi wären optimal. Für die weiteren Über­legungen wird das „Haar­gummi” gedanklich an den beiden auf­gemalten Punkten getrennt. Dann hätten wir genau eine „halbe Länge” des ursprüng­lichen Haar­gummis, bzw. die Länge beträgt nur noch π.

Trotz der Verdrillung beschreibt der Kurven­verlauf in der „Vorder­ansicht” ein Ellipsen­segment.

Abb. 3: In der Vorderansicht beschreibt der Kurvenverlauf ein „Ellipsensegment”.

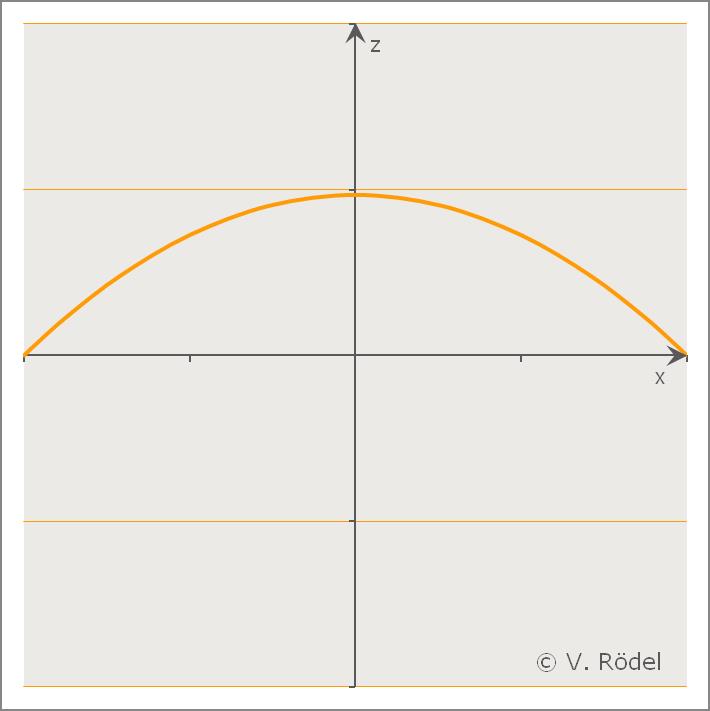
Die verdrillte Haar­gummi­hälfte könnte man, ähnlich wie in der Abhandlung von Minkowski, als „Weltlinie” bezeichnen, die sich um die z-Achse windet, und der t-Achse (Zeit) unserer gedachten Teilchen­scheibe entspricht.

Abb. 4: Der Kurvenverlauf ist in allen Raumrichtungen gekrümmt.

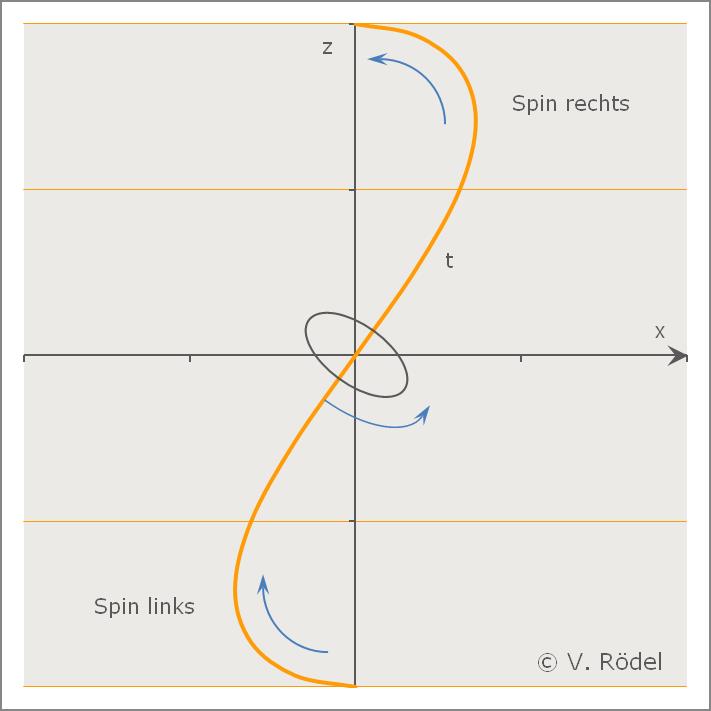
Wie wir fest­stellen können, hat unsere t-Achse in positiver Richtung einen Spin rechts und in negativer Richtung einen Spin links. Lassen wir in einem beweg­ten System nicht nur eine, sondern alle Teilchen­scheiben an dieser gekrümmten t-Achse entlanglaufen, ergibt sich allein aus der Geometrie des Kurven­verlaufs ein verblüf­fender Effekt.

Die Teilchen­scheiben beginnen um die t-Achse zu rotieren. Bei einem kom­pletten Durch­lauf, sprich einem Kurven­verlauf von π rotiert eine betrachtete Teilchen­scheibe genau um 36° in positiver Richtung und 36° in negativer Richtung. Das heißt, der komplette Spin ist um 72° verdreht. Diesen Effekt sieht man der Zeit­achse nicht so ohne Weiteres an. Welche weitere Aus­wirkung hat die Anord­nung der Teil­chen­scheiben auf das System?

Ausgehend von einem stationären System sind die Gasmoleküle im Ideal­fall homogen im System verteilt. Mit anderen Worten, die inneren Bindungs­kräfte sind im Gleich­gewicht und nehmen eine optimale Gitter­struktur an.

Wenn wir nun auf einen gedachten zylind­rischen Volumen­körper, der aus lauter über­einander geschich­teten Teilchen­scheiben besteht, einen Impuls ausüben, wird sich eine Stoß­welle von der einen Seite des Körpers zur anderen Seite fort­pflanzen. Am Ende angelangt, wird es bedingt durch die inneren Bindungs­kräfte zu einem Rück­stoß kommen, und die Stoß­welle wandert wieder zurück. Dieser Effekt wieder­holt sich solange, bis die gesamte kinetische Energie aufge­braucht ist.

Wie sehen die inneren Spannungen in einem solchen System aus?

Hierzu über­tragen wir unser Gedanken­spiel eines zylin­drischen Körpers auf einen massiven Rund­stab aus Stahl. Was passiert, wenn man einen solchen Rund­stab zu einem exakten Ring biegt? Das Ergebnis wird erwartungs­gemäß ein Torus sein. Aller­dings wird sich durch den Biege­vorgang die innere mole­kulare Struktur der Gitter­atome verändern. Wie stark sich die inneren Spannungen auswirken, hängt einer­seits vom Quer­schnitt des Rundstabs ab und anderer­seits von dem Biege­radius.

Im Bereich der tangen­tialen Biege­zone an der inneren Rand­zone wird es zu einer Stauchung des Körpers kommen. Die Moleküle werden sich auf­grund der inneren Scher­kräfte quasi gegen­seitig „wegdrücken” und seit­lich ver­schoben. An der gegen­über­liegenden äußeren Rand­zone, also im Bereich der tangen­tialen Biege­zone am Außen­ring, werden die Moleküle dagegen gestreckt. Zusätz­lich versuchen sich die Gitter­atome einer Dehnung zu wider­setzen und werden eben­falls zur Seite hin ver­schoben. Als Folge des Biege­vorgangs wird der Rund­stab, dessen Quer­schnitts­fläche ursprüng­lich dem eines Kreises ent­sprach, jetzt einer Ellipse gleichen.

Kehren wir wieder gedanklich zu unserem verdrillten Zylinder, bestehend aus nahezu unendlich vielen Teilchen­scheiben zurück. Welche Auswirkung hat die weiter oben beschriebene Verdrillung der gekrümmten t-Achse auf die Teilchen­scheiben im System?

Abb. 5: Verlauf der Zeitachse im gekrümmten Raum.

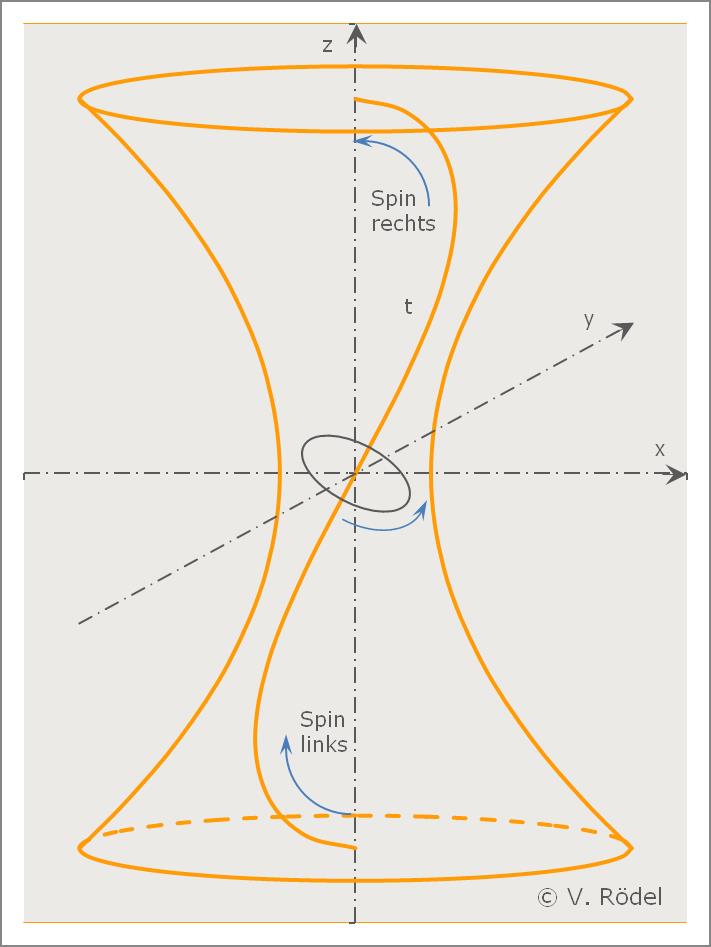
Bei der nach­folgenden Betrachtung ist also unser gesamtes System mit Teilchen­scheiben ange­reichert. Anfäng­lich soll sich die Temperatur auf dem absoluten Null­punkt befinden. Nur die inneren Bindungs­kräfte halten die Moleküle in ihrer Position. Sie befinden sich in voll­ständiger Ruhe und sind im gesamten System homogen angeordnet. In dem System herrscht kein Druck und daher auch keine Temperatur.

Hier sei bereits erwähnt, dass eine derartige Ausgangs­situation völlig von der Urknall­theorie abweicht. Diese geht ja von einer Singularität aus. Als „Singularität” bezeichnet man in der Physik und Astronomie Orte, an denen die Gravitation so stark ist, dass die Krümmung der Raumzeit divergiert, umgangs­sprachlich also „unend­lich” ist.

Die helikale Ring­struktur ist trotz ihrer Verdre­hung bzw. ihres Dralls so geartet, dass sie sich als Gesamt­heit betrachtet in einem Kräfte­gleich­gewicht befindet. Die Torsion folgt ähn­lich wie beim Wachstum der Pflanzen einem Mecha­nismus, bei dem sich Zug- und Druck­kräfte aus­gleichen, sodass Stauchung und Dehnung nun keinen nennens­werten Ein­fluss auf den Quer­schnitt haben. Die Kreis­fläche bleibt trotz der helikalen Ring­struktur nahezu erhalten. Eine ähnlich helikale Struktur lässt sich beim DNA-Strang beobachten, der sich eben­falls in allen Raum­rich­tungen flexibel den jeweiligen Raum­krüm­mungen anpasst.

Bis jetzt haben wir immer noch ein stationäres System vor­liegen, obwohl die Voraus­setzungen für einen 4-dimen­sionalen Raum bereits gegeben sind. Des Weiteren haben wir noch kein geschlos­senes System in Betracht gezogen. Ein geschlos­senes System, hätte den Vorteil, dass der Materie­fluss in eine Rich­tung strebt und irgend­wann in der Zukunft wieder an seinem Aus­gangs­punkt vorbei­strömt und unzählige Male um die Zeit­achse rotiert, ähnlich wie bei einer Achter­bahn .

Was passiert, wenn inner­halb des Systems eine dynamische Kraft auf die Teilchen­scheiben ausgeübt wird? Der gigantische Pool aus Wasserstoff­molekülen wird in dem System zunächst in Bewegung versetzt. Aus­gehend von einem Rechts­system rotiert der Materie­fluss um die Zeit­achse t mit einer Rechts­drift. Die Bewegung sorgt bei moderaten Geschwin­dig­keiten für eine laminare Strömung. Das heißt, alle Teil­chen bewegen sich in Schichten, die sich nicht mit­einander vermischen. Das Fluid strömt kontinuier­lich, ohne dass sicht­bare Turbu­lenzen, also keine Verwirbe­lungen oder Quer­strömungen, auftreten.

Wird die Geschwindig­keit dagegen extrem erhöht, haben wir ähn­liche Effekte wie bei der Biegung des Rund­stabs. Die Moleküle versuchen sich den zuneh­menden Scher­kräften zu wider­setzen. Aus der laminaren Strömung wird zunächst eine turbu­lente Strömung, die anfäng­lich nahezu chaotisch aus­sieht. Aber durch die Drift wird sich bei weiterer Erhöhung der Geschwin­dig­keit, ein Wirbel aus­bilden. Zudem wird sich ein trans­versaler Wellen­vorgang ausbreiten.

Eigent­lich können sich trans­versale Wellen nur in Fest­körpern aus­bilden, während sich in Flüssig­keiten und Gasen normaler­weise nur longi­tudinale Wellen aus­breiten, weil in Gasen Scher­kräfte keine Rolle spielen. Das trifft aller­dings nur auf moderate Geschwindig­keiten zu. Bei heran­nahen an die Licht­geschwin­dig­keit kommt es durch­aus zu Scher­spannungen. Aus der Relativitäts­mechanik wissen wir zum Beispiel, dass das Licht ein trans­versaler Wellen­vorgang ist, obwohl es sich dabei auch nicht um einen Fest­körper handelt. Und es gibt auch keinen Äther, durch den sich das Licht ausbreitet. Auf jeden Fall wird die Strömung einen hyper­bolischen Charakter aufweisen.

Am besten lässt sich das mit der Form eines Tornados beschreiben. Der Tornado besitzt einen oberen Trichter, der nach unten hin hyper­bolisch zuläuft. Aufgrund dieser Form herrschen in allen Bereichen der Luft­strömung unter­schiedliche Geschwin­dig­keiten. Das gleiche lässt sich auch bei größeren Gebilden, wie beispiels­weise einem Wirbel­sturm (Hurrikan) beobachten. Hierbei verläuft ledig­lich der hyper­bolische Trichter flacher. Selbst auf Galaxien lässt sich das gleiche Prinzip über­tragen. Und wenn wir in ganz großen Dimen­sionen denken, lassen sich Wirbel­strukturen und die Gesetze der Wirbel­dynamik selbst auf unser Universum über­tragen. Doch dazu später mehr.

Wie wir bereits heraus­gestellt haben, müssen wir bei einem 4-dimen­sionalen gekrümmten Raum im Ideal­fall ein geschlos­senes System voraus­setzen. Dies gelingt uns, wenn wir das zuvor betrachtete einzelne Zylinder­segment, oder um bei unserem Gedanken­spiel zu bleiben die Haar­gummi­hälfte, sooft aneinander­reihen, bis sich ein verdrillter Voll­kreis ergibt. Und tatsäch­lich erhalten wir bei 5 Segmenten mit jeweils einer Teil-Rotation von 2 × 36° = 72° multi­pliziert mit der Gesamtzahl an Segmenten eine volle Rotation von 360°.

Würde eine Teilchen­scheibe in einem geschlossen System einen kompletten Umlauf des Voll­kreises voll­ziehen, würde sie um die gekrümmte t-Achse ihrer­seits einmal, nämlich 5 x 72° = 360° um die eigene Achse rotieren. Dieser Effekt bleibt unab­hängig der Geschwin­dig­keit des Systems erhalten. Aller­dings verändert sich bei zuneh­mender Geschwin­dig­keit, insbe­sondere bei heran­nahen an die Licht­geschwin­dig­keit, die innere Struktur. Bezogen auf ein Segment von 72° bilden sich zwei hyper­bolische Schalen aus, wie sie von Minkowski beschrie­ben wurden. Wie das im Detail aussieht, werden wir in späteren Kapiteln visualisieren.

Vorweg können wir aller­dings schon jetzt sagen, dass dem System von außen ein über­geordneter Dreh­impuls aufge­prägt wird. Da dieser Dreh­impuls aufgrund des Drehimpuls-Erhal­tungs­satzes insgesamt nicht verloren geht, über­trägt er im Verlauf weitere logarith­misch verlaufende Dreh­impulse an die innere Struktur.

Eine visuelle Vorstellung von dem hier Betrachteten erhält man unter nachfolgendem Link.

⇦ Kapitel Kapitel ⇨