„Wirbel­strukturen” sind etwas All­gegen­wärtiges in unserer unmittel­baren Umgebung und in der Natur. Nicht immer erschlie­ßen sich Wirbel bzw. Strudel so offen­sicht­lich wie zum Beispiel der Wasser­wirbel in einem Wasser­abfluss. Oder beim Auflösen von Zucker mit einem Löffel in einem Trink­gefäß. Und wir können Wirbel­schleppen gut sichtbar an einem startenden oder landenden Flug­zeug beobachten.

Wenn sich Wetter­fronten bilden, ent­stehen manch­mal gewaltige Wirbel in Form eines Tornados oder bilden sich sogar zu einem Hurrikan aus. Im Makro­kosmos sind Galaxien in Wirklich­keit gigan­tische Spiral­wirbel. Im Mikrokosmos lassen sich quanten­mecha­nische Effekte durch Wirbel­strukturen beschreiben. Und selbst der Aufbau unseres Sonnen­systems und sogar die Struk­turen im Universum beruhen auf den gleichen Gesetz­mäßig­keiten.

Man könnte obige Auf­zählung um ein Viel­faches erweitern. Letzt­lich bleibt aber die Frage im Raum stehen, welches physika­lische Gesetz beschreibt diese Phäno­mene? In den vorherigen Kapiteln dieses Bereiches konnten wir sehen, dass es offen­sicht­lich „Goldene Prinzipien” gibt, und dass die Natur einem Gesetz zu folgen scheint, welches man überall wieder­findet.

Vorder­gründig scheinen es nur 2-dimen­sionale Spiral­muster zu sein. Aber in Wirk­lich­keit sind es Wirbel­struk­turen, die mathe­matisch in beiden Rich­tungen einen Grenz­wert gegen unend­lich zu bilden scheinen. In der Reali­tät erreichen alle Wirbel­durch­messer aber nur einen end­lichen Maximal­wert und im Innern einen end­lichen Minimal­wert. Sonst wären Pflanzen mit ihren Blüten­körben unend­lich groß. Auch Wirbel­stürme und Galaxien wären eben­falls unendlich groß. Aber selbst unser Sonnen­system kann nur eine maximale Größe erreichen, die mit dem Kuiper­gürtel bzw. mit der Oortschen Wolke seine maximalen Ausmaße erreicht.

Als „Wirbel” oder „Vortex” bezeichnet man in der Strö­mungs­lehre eine drehende Bewegung von Fluid­elementen um eine gerade oder geschwungene Dreh­achse. Wirbel werden durch gekrümmte Wände ein­geleitet, durch äußere Kräfte ange­facht, durch die Dreh­impuls­erhaltung erzwungen oder sind eine Konse­quenz des Aus­gleichs­bestrebens sich selbst über­lassener Fluide. So besagt es der 2. Haupt­satz der Thermo­dynamik.

Runde Einfas­sungen wie bei einem Glas oder der Stufen­sprung bei einer Wasser­walze leiten Strö­mungen im Kreis. In der Aero- und Hydro­dynamik ent­stehen Wirbel, wenn sich ein Fahr­zeug durch ein Fluid bewegt. Bekann­teste Beispiele sind, wenn sich ein Auto oder ein Flug­zeug durch die Luft bzw. ein Schiff durch das Wasser bewegt. Wenn es zu Strömungs­abrissen an der A-Säule von Autos kommt, ent­stehen dauer­hafte Wirbel­strömungen.

So sind es insbe­sondere Träg­heits­kräfte in Fluiden, die das Medium in Rotation ver­setzen. Der Coriolis­effekt in der Erdatmo­sphäre lenkt zum Beispiel Strömungen inner­halb des Luftkörpers in eine Kreis­bewegung um. Dies ist auch die Ursache dafür, dass Hoch- und Tief­druck­gebiete in der Atmo­sphäre Wirbel bilden.

Wenn Fluide auf ein Zentrum zustreben, dann können Fluid­ele­mente, die einen Dreh­impuls besitzen, nicht ein­fach gerade­wegs hinein stürzen. Die Erhaltung des Dreh­impulses zwingt sie erst auf eine Kreis­bahn um das Zentrum, wodurch im inter­stellaren Raum proto­planetare Scheiben, soge­nannte Akkre­tions­scheiben ent­stehen. Das sind Wirbel aus Staub und Gas, die sich um junge Sterne im Zentrum bilden.

Nur indirekt von äußeren Ein­flüssen geleitet ent­stehen Wirbel, wenn Fluid­massen mit unter­schied­lichen Eigen­schaften auf­einander treffen. Die Fluid­massen können sich unter anderem in ihrer Tempe­ratur, ihrer Geschwin­dig­keit oder ihrer Dichte unter­scheiden. An den Grenz­flächen zwischen den Fluid­massen kommt es bei hin­reichender Differenz in den Eigen­schaften (am Kipp-Punkt) zu Instabilitäten, die zu Wirbeln und im weiteren Verlauf zu turbu­lenter Strö­mung führen, in der schließ­lich unter­schied­lich große Wirbel die Massen intensiv durch­mischen.

Ein solches Phäno­men ist die Kelvin-Helmholtz-Instabi­lität zwischen zwei unter­schiedlich schnellen Strö­mungen oder die Rayleigh-Taylor-Instabi­lität zwischen zwei unter­schiedlich schweren Flüssig­keiten. Die Durch­mischung führt zu einem Aus­gleich des Gefälles, es sei denn, äußere Ein­flüsse halten das Gefälle aufrecht. Dann können andauernde, kreisende Konvektions­zellen entstehen.

„Wirbel” bilden in der Regel keine stationäre Strömung, sondern sie ändern oft ihre Form und bewegen sich als Ganzes fort. In diesem Fall bewegen sich die Fluid­elemente nicht auf geschlos­senen Kurven. Viel­mehr gleichen sie eher Schrauben­linien oder Zykloiden. Die Dreh­achse der Wirbel, sprich die analog zur Strom­linie defi­nierte Wirbel­linie, kann eine gebogene, sich windende und als Ganzes bewegende Linie wie bei einem Tornado sein. Die drehende Bewegung kann mit einem zum Zentrum hin oder weg gerichtetem Fluss kombiniert sein. Sehr schön lässt sich das an einem Wasser­strudel bei Abflüssen beobachten. Ein rein kreisender Wirbel ohne eine radiale Geschwin­dig­keits­komponente wird quellen­frei genannt.

Wegen der Dreh­impuls­erhaltung können Wirbel nicht ohne Weiteres auf­hören oder sich zu drehen beginnen. Wirbel, die sich auf­gelöst haben, bleiben ver­schwunden (1. Helmholtz'scher Wirbel­satz). Die Kreis­bewegung eines Rings aus Fluid­elementen ist eine Erhaltungs­größe (Kelvin'­scher Wirbel­satz). Diese Zirku­lation ist über die Länge einer Wirbel­röhre konstant (3. Helmholtz'scher Wirbel­satz). Daher neigen Wirbel dazu, aus­gedehnte Wirbel­röhren im Fluid auszu­bilden. Durch Reibung­seffekte und Umwand­lung in thermische Energie lösen sich reale Wirbel mit der Zeit auf und die Zirku­lation nimmt stetig ab.

Die Fluid­elemente werden vom Wirbel mit­geführt (2. Helmholtz'scher Wirbel­satz). Auf diese Weise können Wirbel die Masse, den Dreh­impuls und die Energie über größere Ent­fernungen mit nur geringen Ver­lusten trans­portieren. Ein klassisches Experiment sind die Rauch­ringe.

In größeren Wirbeln drehen sich die Fluid­elemente nicht mehr um sich selbst, sondern werden im Kreis parallel ver­schoben. Diese Tatsache führt zwischen den Fluid­elementen zu Scherungen, die zum Zentrum des Wirbels hin zunehmen. Die Visko­sität ver­ringert diese Scherung im Zentrum des Wirbels oder in kleinen Wirbeln, so dass es dort zu einer quasi-starren Rotation kommt.

In einem Fluid mit niedriger Visko­sität ist in einer stationären Strömung, wenn man die äußeren Kräfte vernach­lässigt, die Summe aus kinetischer Energie und dem statischen Druck ent­lang einer Strom­linie konstant. Der statische Druck, ist der Druck, den ein mit der Strömung mit­bewegtes Fluid­element ver­spürt. In größeren Wirbeln nimmt die Strö­mungs­geschwin­dig­keit zum Zentrum hin zu, wes­wegen der statische Druck dort abnimmt.

In einem realen Gas geht in einem konstanten Volumen der geringer werdende Druck mit geringer werdender Tempe­ratur einher. Deshalb ist die Tempe­ratur im Zentrum am niedrigsten. Das ist auch ein Grund dafür, warum am Flug­zeug Kondens­streifen sicht­bar werden. Die Wirbel­stärke ist in den Rand­zonen an den Flügel­spitzen am größten und dort bilden sich klar umrissene Wirbel­röhren. Die Inten­sität der Wirbel­röhren nimmt zum Rumpf hin ab.

„Wirbel” sind der Haupt­bestand­teil „turbulenter” Strö­mungen aber nicht jeder Wirbel gehört zu einer turbu­lenten Strö­mung. Turbu­lente Strö­mungen beinhalten auf allen Größen­skalen Wirbel, die sich schein­bar ungeordnet bewegen. Bei genauer Betrachtung zeigt sich jedoch, dass bei Einbe­ziehung der Reynolds-Gleichung die Geschwin­dig­keit eines Fluids in einen Mittelwert und einen statis­tischen Schwankungs­wert auf­geteilt werden kann. Der zeit­unab­hängige Mittel­wert berück­sichtigt die stationären Wirbel, wogegen der Schwankungs­wert die zufäl­ligen, fluktu­ierenden Wirbel ein­bezieht.

Ein Grenz­fall sind perio­dische Ablö­sungen von Wirbeln wie in einer soge­nannten Wirbel­straße, die hinter einem umströmten Zylinder bei nicht zu großer Reynolds­zahl entsteht. Der Zylinder wird zunächst laminar und wirbel­frei umströmt. Bei zunehmender Strö­mungs­geschwin­dig­keit bilden sich periodische Ablö­sungen. Es lösen sich wie bei einem charakte­ristischen Muster abwech­selnd links- und rechts­drehende Wirbel ab. Diese Wirbel sind weder stationär noch chaotisch.

Mit steigender Anströ­mungs­geschwin­dig­keit geht die Wirbel­straße dann in eine turbu­lente Strömung über. Es treten nach und nach mehr Wirbel auf, so dass der Strö­mungs­wider­stand ansteigt. Beim Über­gang zur Turbu­lenz variieren die Größe der Wirbel und die Zeit­punkte ihrer Ablösung immer mehr. Bei voll aus­gebildeter Turbu­lenz sind Wirbel auf allen Größen­skalen vor­handen. Bei einer Reynolds­zahl Re ≈ 3 · 10⁵ wird auch die Grenz­schicht turbu­lent und der Wider­stand fällt abrupt ab um dann wieder anzu­steigen.^[1]

Der „Potential­wirbel” oder auch „freie Wirbel” genannt ist ein klassi­sches Beispiel einer rotations­freien Potential­strömung. Große Wirbel in Fluiden mit niedriger Visko­sität lassen sich mit diesem Modell gut beschreiben. Die Winkel­geschwin­dig­keit in diesen Wirbeln ist in ihrem Zentrum am größten, wobei anderer­seits der Druck am kleinsten ist. Wegen dieser, verzerrten Geschwindig­keits­verteilung werden die Fluid­elemente verformt.

Weil die Rotation des Geschwin­dig­keits­feldes gemäß ...

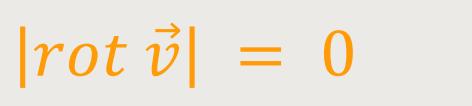
... verschwindet, zeigen die Fluid­elemente trotz ihrer kreisenden Bewegung im Wirbel immer in dieselbe Richtung.

Wenn man mathe­matisch genau ist, gilt die obige Gleichung aller­dings nur außer­halb des Zentrums, also für (x, y) ≠ 0, während bei Mit­ein­beziehung des Zentrums ...

... gilt, mit der 2-dimen­sionalen Diracschen Delta­funktion und der Wirbel­stärke _₀.

Wegen dieser totalen Rota­tions­freiheit für alle Punkte außer­halb des Zentrums kann lokal nicht auf eine Wirbel­bewegung geschlossen werden. Erst die Beobach­tung eines größeren Gebietes oder über längere Zeit­räume gestattet es, diese Wirbel zu erkennen. In der numerischen Strömungs­mechanik ist das kleinste betrachtete Volumen das finite Volumen für das sogenannte Wirbel­kriterien formuliert wurden, um Wirbel von Scher­schichten zu unter­scheiden.

Wie sich das im Detail inter­pretieren lässt, wird in einem anderen Kapitel näher beleuchtet.

Ein „Fest­körper­wirbel” bildet sich zum Beispiel, wenn sich nach entspre­chend langer Anlauf­zeit eine Flüssig­keit in einem Gefäß auf einem Dreh­teller mit konstanter Winkel­geschwin­dig­keit ω als starrer Körper dreht. Mit­bewegte Fluid­teil­chen drehen sich um ihre eigene Achse, ohne verformt zu werden. In einem Fest­körper­wirbel gilt:

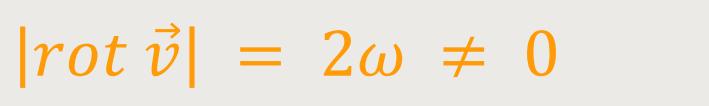
Alle Fluid­partikel bewegen sich wie beim Potential­wirbel auf konzen­trischen Kreis­bahnen, aber die Geschwin­dig­keits- und Druck­ver­teilung sind jeweils völlig andere. Die Geschwin­dig­keit ist außen am größten und innen am lang­samsten, so dass der Druck außen am niedrigsten und innen am höchsten ist.

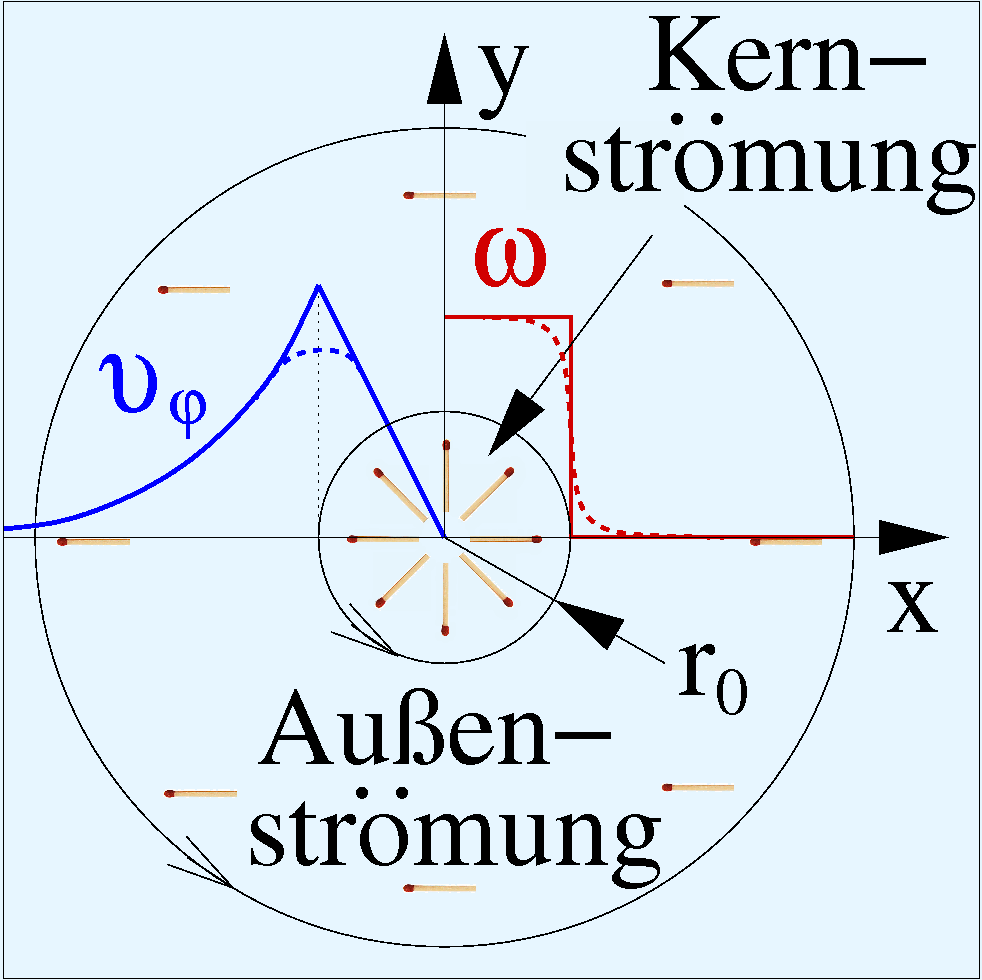
Der „Rankine-Wirbel”, benannt nach William J. M. Rankine, ist ein Wirbel­modell, das den Poten­tial­wirbel im Außen­bereich mit dem Fest­körper­wirbel im Zentrum verbindet^[2]. Der Poten­tial­wirbel beschreibt näm­lich eine Aus­fluss­strö­mung im Außen­bereich gut, wo die Umfangs­geschwin­dig­keit v_φ mit dem Radius abnimmt und keine Rotation vor­liegt:

Mit Annähe­rung der Fluid­elemente an das Zentrum ent­wickeln sich im Poten­tial­wirbel unrealistisch hohe Scher­geschwin­dig­keiten im Fluid. Im Rankine-Wirbel verhindern Zähig­keits­kräfte unter­halb eines gewissen Kern­radius r_₀ die Scherungen und es kommt zu einer quasi-starren Drehung.

Abb. 1: Skizze eines Rankine-Wirbel

Inner­halb des Kern­radius ist die Umfangs­geschwin­dig­keit daher propor­tional zum Radius und die Rotation ω ist konstant ungleich Null. In realen Fluiden verläuft der Über­gang von der Außen- in die Kern­strömung nicht abrupt, sondern glatt. Der Effekt der außen fehlenden und innen vor­handenen Rotation der Teil­chen lässt sich z. B. durch mitschwimmende Streich­hölzer nachweisen.

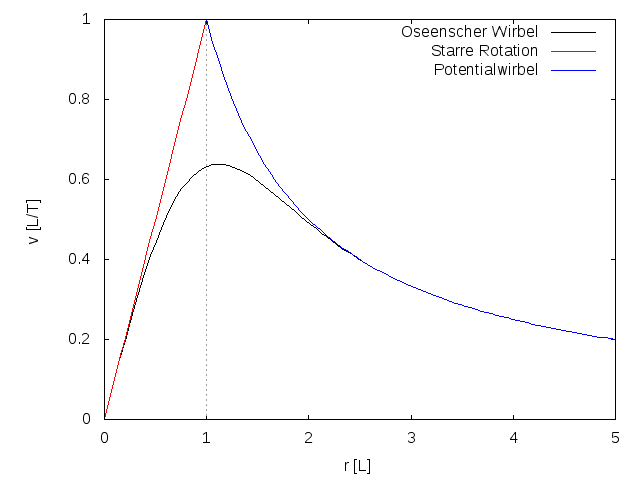
Der Hamel-Oseensche-Wirbel, benannt nach Carl Wilhelm Oseen und Georg Hamel, ist ein Wirbel­modell, das die Navier-Stokes-Gleichungen exakt erfüllt, die die Strömung realer Fluide gut beschreibt. Das Fluid strömt rein kreis­förmig jedoch zeit­abhängig, instationär um das Wirbel­zentrum. Die Visko­sität zehrt die kinetische Energie des Wirbels mit der Zeit auf und die Strö­mungs­geschwin­dig­keit nimmt monoton mit der Zeit ab. Zu Beginn der Bewegung oder im Grenz­fall verschwin­dender Visko­sität ist der Wirbel ein Potential­wirbel. Ansonsten ist das Geschwin­dig­keits­profil des Hamel-Oseenschen-Wirbels beschränkt und ent­spricht im Wirbel­kern, sowie im Außen­bereich einem Rankine-Wirbel.

Abb. 2: Umfangsgeschwindigkeit beim Hamel-Oseenschen-Wirbel im Vergleich mit der starren Rotation und dem Potentialwirbel

Bevor wir uns an die Wirbel­strukturen in unserem Universum bis hin zu unserem Sonnen­system heran­wagen, gehen wir im nächsten Kapitel noch kurz auf die Navier-Stokes-Gleichungen ein, weil sie die Strömung realer Fluide gut beschreiben.

Quellen

[1] J. H. Spurk: Strömungslehre. Einführung in die Theorie der Strömungen. 8. überarbeitete Auflage. S. 377 f.
[2] H. E. Siekmann, P. U. Thamsen: Strömungslehre. Springer, 2007, S. 177 f.

Der Text auf dieser Seite basiert auf dem Artikel Wirbel (Strömungslehre) aus der freien Enzyklopädie Wikipedia und ist unter der Lizenz Creative Commons Attribution-ShareAlike 3.0 Unported - Deed verfügbar.


⇦ Kapitel Kapitel ⇨