Wenn es aufgrund des Vorhandenseins eines Dielektrikums zu einer Abschwä­chung des elektrischen Feldes kommt, hat dies auch Auswirkungen auf die Gesetz­mäßig­keiten.

Hierzu schaut man sich die Grund­gleichungen an und untersucht, wie sich diese ändern. Denn aus der Maxwell-Gleichung lässt sich letztlich alles Weitere herleiten. Daraus lassen sich sogar Schluss­folgerungen ziehen, wie sich alle anderen Gesetz­mäßig­keiten ändern.

Die Grundgleichung für die Quell­dichte des elektrischen Feldes im Vakuum lautete:

Diese Gleichung besagt, dass die elektrische Ladungs­dichte ϱ , bis auf einen Faktor ε_₀ , die Quell­dichte des elektrischen Feldes ist.

Was anschließend hinzukam, war die Grund­gleichung für das Dielektrikum:

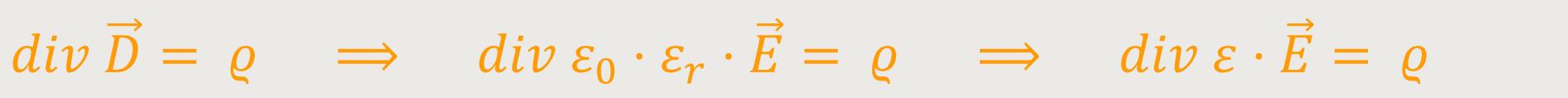
Wobei das ϱ hier nur die Dichte der freien Ladungen ist, denn Polarisations­ladungen blieben hierbei unberücksichtigt.

Der Unterschied beider Beziehungen liegt im Faktor ε_₀ und ε_₀ · ε_r. Wobei man generell für das Dielektrikum nur noch ε schreibt, weil es im Vakuum kein ε_r gibt und daher dem Wert 1 entspricht.

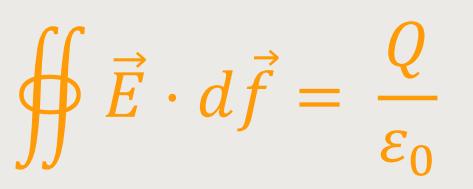
Wenn man den Nenner entsprechend ersetzt, erhält man:

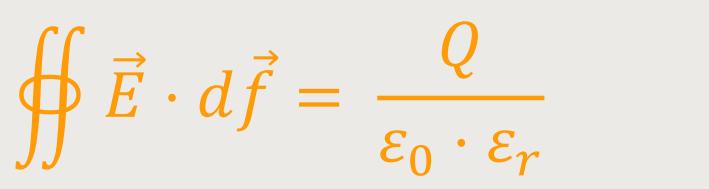
Und wenn man diese Beziehung umformt, ergibt sich:

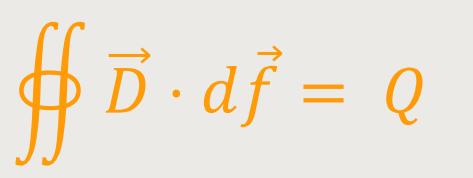
Bei der Umformung wurde lediglich die Material­gleichung verwendet. Im Grunde wird das „Gauß'sche Gesetz” dadurch etwas eleganter, wenn es unter der Verwendung der dielektrischen Verschiebung umschrieben wird.

Bei den Gesetzmäßigkeiten im Vakuum bezieht sich das ϱ nicht nur auf die Dichte der freien Ladungen, sondern auf alle Ladungen. Aller­dings gibt es im Vakuum nichts anderes, als freie Ladungen.

Des Weiteren besagte das „Coulomb-Gesetz”:

Bei dieser Beziehung kann man erkennen, dass die Wechsel­wirkungs­kraft zwischen den Punkt­ladungen um den Faktor 1 /ε_r verringert wird. Bei Wasser wäre das zum Beispiel 1/80. Deshalb eignet sich Wasser sehr gut als Lösungsmittel.

Was passiert, wenn man beispiels­weise Kochsalz im Wasser auflösen möchte? Kochsalz­moleküle bestehen aus Natrium und Chlor, die eine Ionenbindung eingehen. Die „positiven” Natrium-Ionen und die „negativen” Chlor-Ionen werden durch die Coulomb-Kräfte zusammen gehalten. Und wenn man diese Verbindung im Wasser auflöst, wird die Wechsel­wirkungs­kraft um 1/80 reduziert. Daher reicht bereits thermische Energie aus, damit sich die Ionen­bindung voneinander löst. Übrig bleiben Natrium-Ionen und Chlor-Ionen. Mit anderen Worten, das Kochsalz hat sich in dem Wasser aufgelöst. Und weil sich jetzt im Wasser bewegliche Ionen befinden, wird es sogar leitend. (Soweit der Einschub)

Für die elektrische Feldstärke, in der Umgebung einer Punktladung, galt analog:

Und für die Kapazität des Plattenkondensators galt:

In diesem Fall aber nimmt die Kapazität um den Faktor ε_r zu. Bei entsprechender Wahl des Materials zwischen den Platten lassen sich auf diese Weise große Kapazitäten realisieren.

Abschießend besagte die Energiedichte im elektrischen Feld:

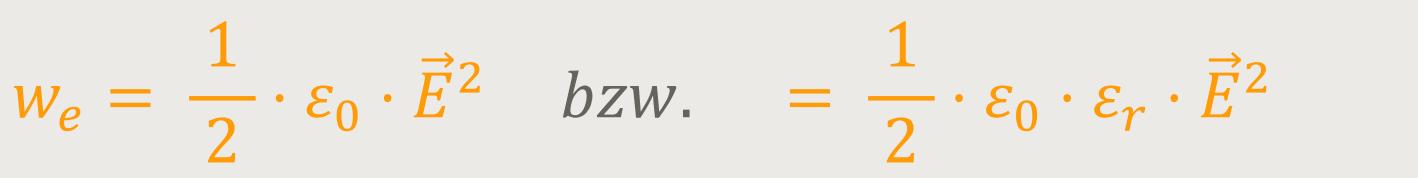
Wenn man das nochmal umformt, erhält man eine wesentliche Grund­beziehung der Elektrodynamik:

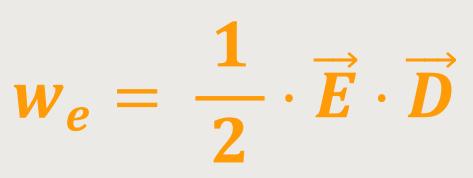
Doch dazu später mehr.

Neben den klassischen Dielektrika gibt es auch kristalline Medien. Mit der bereits angesprochenen Material­gleichung lässt sich auch etwas über die dielektrische Verschiebung dieser Medien aussagen. Weil diese Körper nicht isotrop sind, verlaufen die Vektoren nicht mehr parallel zueinander. Für diesen Fall benötigt man eine tensorielle Schreib­weise, auf die wir wegen ihrer Komplexität nicht näher eingehen. Dennoch lässt sich in diesem Zusammen­hang etwas über die „Elektro­striktion” und den „Piezo-Effekt” sagen.

Bei der Elektrostriktion geht es um einen Effekt, der durch mechanische Deformationen bei einem kristallinen Dielektrikum hervor­gerufen wird. Durch die Deformation können in den Grenz­schichten entgegen­gesetzte Ladungen auftreten. Und wenn man umgekehrt, derartige Werk­stoffe in ein elektrisches Feld bringt, kann es zu Deformationen kommen.

Beim Piezo-Effekt ist es so, wenn man eine mechanische Kraft auf einen Kristall ausübt, kann es zu elektrischen Spannungen in den gegenüber­liegenden Grenz­flächen kommen. Deshalb hat man diesen Effekt gerne bei Quarz­uhren verwendet, indem ein kleiner Quarz­kristall in einen elektrischen Schwing­kreis geschaltet wird. Aufgrund seiner mechanischen Eigen­schaften nutzt man dessen Schwingungs­frequenz. Dadurch entsteht eine wohl definierte Resonanz­frequenz der Spannungen. Das stabilisiert den entsprechenden Schwing­kreis, und man braucht nur noch die Schwingungen zu zählen.

Damit schließen wir das Thema „Elektrostatik” vorerst ab.

⇦ Kapitel Kapitel ⇨