Jetzt wechseln wir von der Elektro­statik zur „Elektro­dynamik”. Im weiteren Verlauf werden wir uns schritt­weise mit den zeit­lich veränder­lichen Prozessen beschäftigen. Bewegte Ladungen, wie das in elek­trischen Strömen der Fall ist, führen zur Aus­bildung von magne­tischen Feldern.

Nennens­werte Magnet­felder treten erst dann auf, wenn Ströme von der Größen­ordnung 1 Coulomb pro Sekunde auft­reten. Insofern kommt es darauf an, derart große Ströme erzeugen zu können. Um das zu realisieren, gibt es zwei wichtige Methoden. Die eine erfolgt elektro­chemisch, also in Form von „galvanischen Zellen”. Und die andere Methode wird durch die „elektro­magnetische Induktion” erreicht. Und dieses Induktions-Gesetz geht auf Faraday zurück.

Aber bereits kleine galvanische Zellen sind in der Lage, Ströme von einigen Ampere zu erzeugen.

Eine Möglich­keit der Reali­sierung sind bewegte Ladungs­träger im Vakuum. Hierzu erzeugt man zum Beispiel Elektronen­strahlen, und lässt diese durch eine evakuierte Röhre durch­strömen. Alter­nativ bietet sich auch ein hoch­verdünntes Gas an, wie in Leucht­stoff­röhren:

Wenn man aller­dings stärkere Ströme trans­portieren will, verwendet man dazu vorzugs­weise metal­lische Leiter. Da gibt es einer­seits elektro­nische Leiter, in deren Innerem sich Elektronen frei bewegen können, und damit den Ladungs­transport ermög­lichen. Aber auch Halb­leiter gehören dazu, die ebenfalls zu den Fest­körpern zählen.

Des Weiteren gibt es Ionen­leiter, bei denen nicht nur Elektronen, sondern auch negative und/oder positive Ionen frei beweg­lich sind. Man spricht dann von den sogenannten „Elektrolyten”, also Flüssigkeiten.

Und dann gibt es noch die gemischten Leiter. Die enthalten alles, was sich zum Ladungs­transport eignet, Elektronen und +/- Ionen. Solche Vorgänge sind in Gasent­ladungen und Plasmen zu beobachten.

Wie werden uns über­wiegend mit dem Ladungs­transport in elektro­nischen Leitern auseinander­setzen, weil das für die Praxis mehr von Bedeutung ist. Das sind zum Beispiel längliche, dünne Kupferdrähte.

Zu Beginn führt man hierzu zunächst die „elektrische Stromstärke” ein:

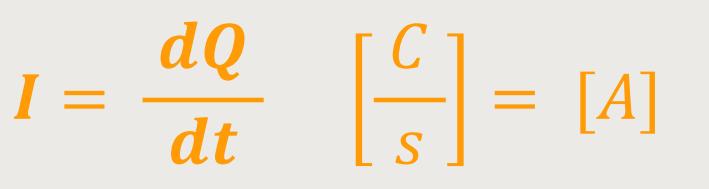
Darunter versteht man die Ladung, die pro Zeit­einheit durch den Quer­schnitt des betreffenden Leiters hindurch­tritt. Andre-Marie Ampere war der erste, der Kraft­wirkungen zwischen zwei strom­durch­flossenen Leitern beobachtet hatte. Und diese Kraft­wirkungen verwendet man heute als Definitions­grundlage für die Einheit von 1 Ampere. Heute definiert man es mehr über die Kraft­wirkungen zwischen parallelen gerad­linigen Leitern.

Ist die Strom­stärke bekannt, kann man auch die „Strom­dichte” definieren.

Wenn ein Leiter einen gewissen Quer­schnitt hat, durch den eine Ladung fließt, also eine gewisse Ladungs­menge, die pro Zeit­einheit den gesamten Quer­schnitt durch­setzt, lässt sich das auf die Einheit des Quer­schnittes beziehen. Mit anderen Worten, wie viel Ladung fließt pro Zeit und Querschnitts­einheit durch diesen Leiter hindurch.

Die Strom­dichte ist dem­nach die Strom­stärke pro Querschnitts­fläche:

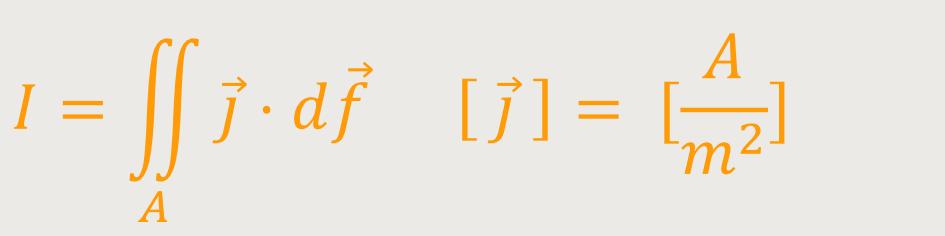
  ist die Stromdichte

Die Ladungs­dichte ϱ, und die Strom­dichte können in Summe als Ursachen des elektro­magnetischen Feldes aufge­fasst werden. Wie wir schon betrachtet haben, ist ϱ die Quell­dichte des elektrischen Feldes, und ist daher für die elektrische Komponente verant­wortlich. Dagegen ist es bei dei der Strom­dichte so, dass elektrische Ströme zur Ausbildung von magne­tischen Feldern führen. Während ϱ eine skalare Größe ist, handelt es sich bei um eine vektorielle Größe.

Diese vier Größen zusammen sind ein Gegen­stück zu den drei Raum­dimensionen und der einen Zeit­dimension. Im tensoriellen Formalismus wird dies in einen „Vierer­strom” zusammen­gefasst.

Wie hängt jetzt die Strom­dichte mit der Geschwindig­keit der Ladungs­träger in einem Leiter zusammen?

Grafik (wird später eingefügt)

Hierzu kann man sich einen dünnen zylin­drischen Leiter denken, mit einem entsprechenden Quer­schnitt. Auf der Querschnitts­fläche liegt ein Flächen­vektor , dessen Länge dem Fläche­ninhalt entspricht, wobei er senk­recht auf die Querschnitts­fläche in Richtung des Leiters zeigt. Und dann gibt es noch parallel dazu den Geschwindigkeits­vektor der Ladungs­träger , die durch den Leiter hindurch­fließen.

Wie stellt sich der Zusammenhang im Detail dar?

n   ist die Anzahl der Ladungen q pro Volumeneinheit
  ist die Geschwindigkeit der Ladungen
 ist der Vektor der Querschnittsfläche

Damit ergibt sich zunächst für die Stromstärke:

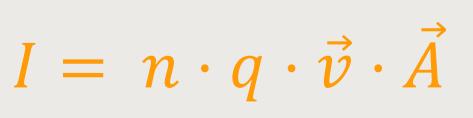
n · q   ist die Ladungsdichte ϱ
·   ist das Volumen pro Zeit

Insofern lässt sich auch schreiben:

Denn wenn konstant ist, kann man es vor das Integral setzen, oder so wie formuliert ausdrücken.
Demnach entspricht:

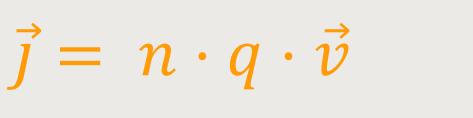
Somit wird die Stromdichte definiert als:

Auf diese Weise kommt man zu einer einfachen Darstellung für die Stromdichte.

Wie schnell bewegen sich nun die Ladungs­träger in einem Strom­leiter, beispiels­weise einem dünnen Kupferdraht?

Nehmen wir folgende Werte an (Kupferdraht):

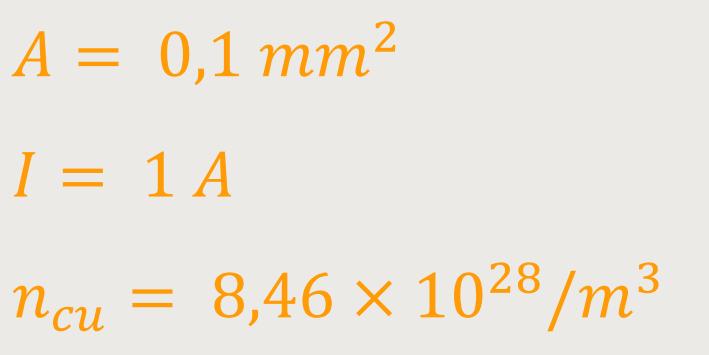
Damit ergibt sich:

q   ist entspricht der Elementarladung e

Damit lässt sich obige Beziehung umschreiben:

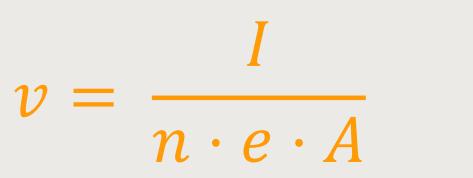
Daraus ergibt sich:

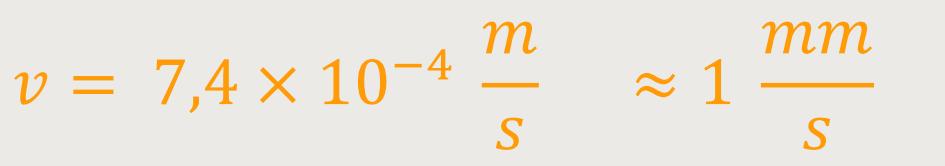
Das ist im Grunde eine sehr langsame Geschwindigkeit.

Warum hat man den­noch das Empfinden, dass der Strom durch die Leitung schießt? Nun, der Leiter ist voll von diesen Elektronen. Und wenn ein Feld angelegt wird, breitet sich das Feld rasch aus. Die Elektronen bewegen sich praktisch alle gleich­zeitig.

Man kann davon ausgehen, dass Ladungen nicht erzeugt oder vernichtet werden, sondern nur getrennt werden können. Die „Erhaltung der Ladung” ist so etwas Ähn­liches wie die Erhaltung der Masse. Bei der Hydro­dynamik war es so, dass man aus der Erhaltung der Masse eine Kontinuitäts­gleichung hergeleitet hat. Zwischen der Massen­dichte in dem strömenden Fluid und dem Vektor . Hier steht dieser Vektor für die Massen­strom­dichte.

Genau das Gleiche kommt jetzt zum Tragen. Es wird einer­seits die Ladungs­dichte und anderer­seits die Strom­dichte mitein­ander in Beziehung gesetzt. Das heißt, aus der Erhaltung der Ladung muss sich eine Beziehung zwischen ϱ und ergeben.

Dazu betrachtet man ein gewisses Volumen V. Und in diesem Volumen gibt es die Ladungs­träger Q.

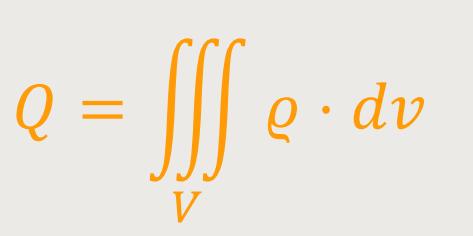
Das bedeutet, aus dem Volumen heraus, quasi durch die Ober­fläche des Volumens hindurch, tritt eine Ladung aus. Und die Ladung, die pro Zeit­einheit heraus­tritt ist der elektrische Strom:

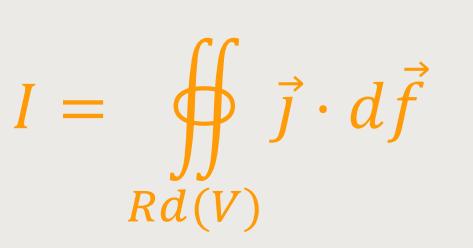
Wenn aber nun etwas heraus­strömt, dann ist zwangs­läufig nachher weniger drin.

Für die Ladungs­erhaltung gilt daher:

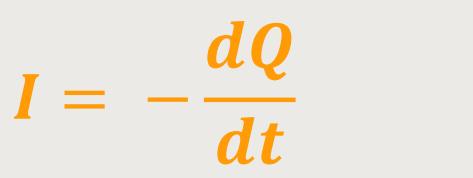
Der heraus­fließende Strom führt somit zu einer Verringerung der Ladung.

Jetzt möchten wir diese integrale Beziehung in eine differen­tielle Beziehung umsetzen:

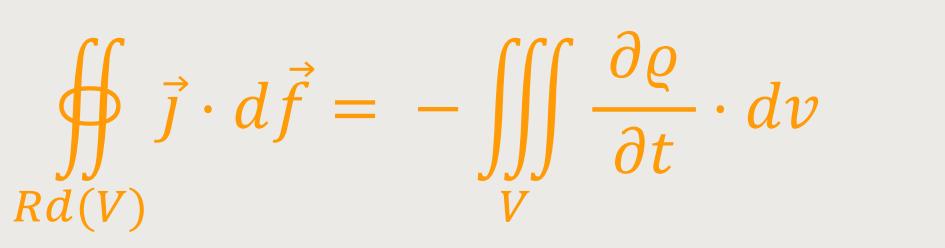
Im vorliegenden Fall wurde ein partielles Differentiations­zeichen verwendet, weil die Ladungs­dichte ϱ nicht nur von der Zeit, sondern auch von den Orts­koordinaten abhängig ist. Wir schauen uns hier aber nur die Ableitung nach der Zeit an.

Obiges Flächen­integral lässt sich mithilfe des Gauß'schen Integral­satzes umformen:

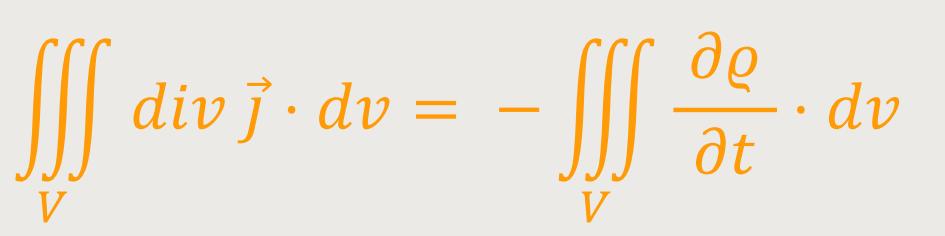
Damit erhält man:

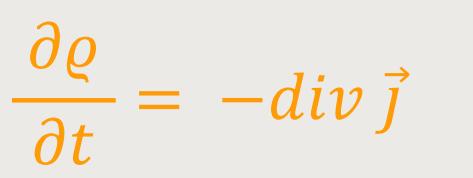
Oder es ergibt sich entsprechend:

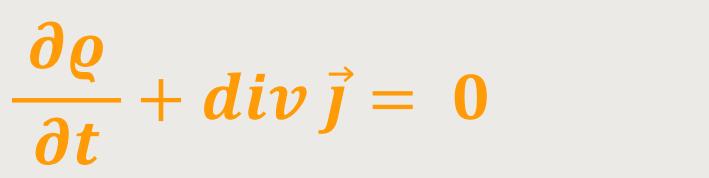
Das ist die gleiche Herleitung wie in der Hydro­dynamik, und wird auch als die „Kontinuitätsgleichung” bezeichnet. Mit dieser Beziehung wird der Zustand der Ladungs­erhaltung beschrieben. Denn wenn es eine gewisse Quell­stärke aus einem Volumen heraus gibt, dann wird die Dichte in dem Volumen zurück­gehen. Die Ladungs­erhaltung ist eine Konsistenz­beziehung zwischen ϱ und .

Wenn wir später die Konsistenz der Maxwell-Gleichungen betrachten, werden wir auf obige Beziehung zurück­greifen. Denn erst in einer dieser Maxwell-Gleichungen werden wir auf einen Zusatz­term stoßen, den sogenannten „Maxwell'schen Verschiebungsstrom”, der letztlich die Existenz elektro­magnetischer Wellen ermöglicht.

⇦ Kapitel Kapitel ⇨