Wie wir im vorherigen Kapitel betrachtet haben, versteht man unter der Divergenz einen bestimmten „Differential­operator”. Dieser Operator gibt letztlich die „Quell­dichte” an. Also, wenn man ein kleines Volumen in einem elektrischen Feld betrachtet kann man ermitteln, wie groß der Fluss dieses elektri­schen Feldes aus dem Volumen heraus, durch die Ober­fläche dieses Volumens hindurch, nach außen ist. Und dieser Fluss pro Volumen­einheit ist quasi die Quelldichte bzw. Divergenz.

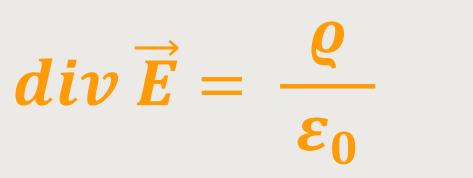
Und damit erhält diese Gleichung eine äußerst anschau­liche Bedeutung nämlich, dass die Quell­dichte des elektri­schen Feldes bis auf den Faktor ε_₀ (eine universelle Konstante) gleich der Ladungs­dichte in dem betrachteten Raum ist. Somit stehen Ladungen und elektrische Felder in einem engen Verhältnis zueinander. Denn die Ladungen sind die Quellen des elektrischen Feldes.

Nun ist man aber auch daran interes­siert, bei vorge­gebenen Ladungs­dichte­verteilungen die zugehörigen elektrischen Felder zu berechnen. Dazu ist es allerdings sinnvoll, dieses elektrische Feld auf ein Potential zurückzuführen.

Hierzu wollen wir zunächst die „potentielle Energie” betrachten. Es geht zu Beginn um die Frage, was ist die potentielle Energie einer Probe­ladung q in einem elektrischen Feld. Bei den Kräften in der Mechanik war es so, dass man die potentielle Energie nur dann sinnvoll einführen konnte, wenn man sich auf ein konser­vatives Kraftfeld bezieht. Für nicht konser­vative Kräfte ist die Einführung einer potentiellen Energie nicht möglich.

Elektrische Felder sind aber im Allgemeinen keine konser­vativen Kraftfelder. Nur in der Elektro­statik sind die elektri­schen Felder konservativ, und deshalb lassen sich ein elektri­sches Potential und eine potentielle Energie einer Probe­ladung einführen. Wenn man dagegen zeit­abhängige Felder betrachtet, zum Beispiel bei Induktions­vorgängen, treten dort elektrische Felder auf, die nicht konservativ sind.

Die potentielle Energie an einem bestimmten Punkt in diesem elektri­schen Feld ist, genauso wie in der Mechanik, nichts anderes, als die Arbeit die verrichtet werden kann, wenn man die Probe­ladung zu einem fest gewählten Bezugs­punkt P₀ hin bewegt. Die poten­tielle Energie eines Körpers in einem Kraft­feld ist somit die Arbeit, die verrichtet werden kann, wenn dieser Körper von dort, wo er ist, sich zu dem Bezugs­punkt bewegt.

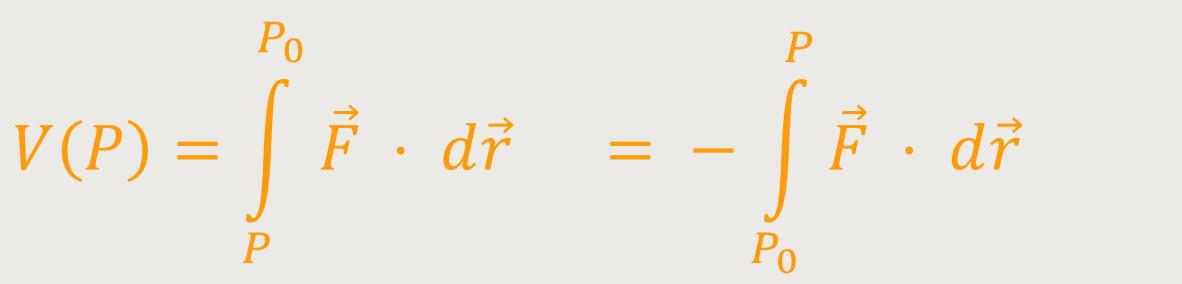
Beide Schreib­weisen sind möglich, je nachdem, ob die Arbeit erst vorrichtet werden muss, oder bereits verrichtet wurde. Denn im zweiten Fall muss eine Gegenkraft berück­sichtigt werden. Der Bezugs­punkt P_₀ wird oft im Unendlichen gewählt, weil sich das Integral sonst nicht anschaulich ausrechnen lässt.

Für eine Punktladung einer felderzeugenden Ladung Q ergibt sich daher:

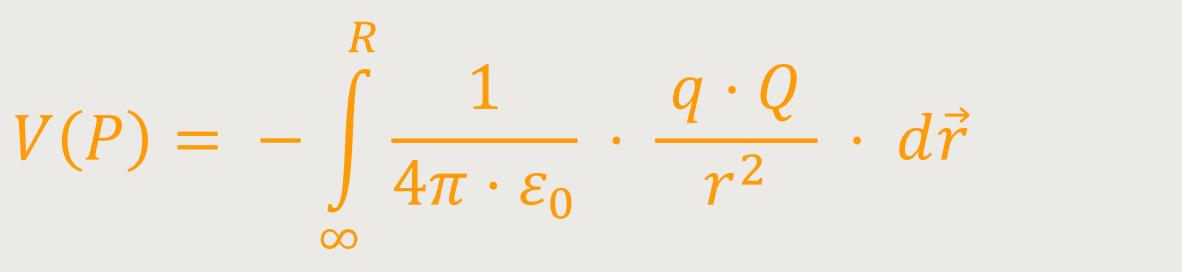
Also, der Punkt P liegt im Abstand R von der feld­erzeugenden Ladung Q, und man betrachtet die poten­tielle Energie in diesem Feld. Und für die Kraft wurde die Beziehung für die Feld­stärke eingesetzt.

Für die potentielle Energie der Probeladung q im Abstand R bleibt übrig:

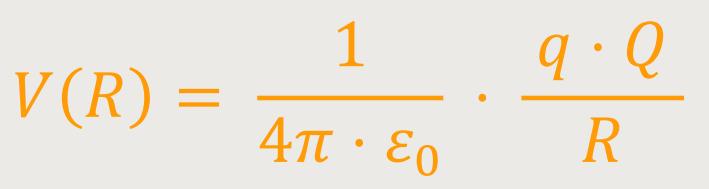
Zur Erklärung: Es wurde 1 /r² integriert und damit ist −1 /r herausgekommen. Dann haben wir den Hauptsatz der Integral­rechnung angewendet, nämlich die Stamm­funktion an der oberen Grenze minus der Stamm­funktion an der unteren Grenze

Betrachtet man gleichnamige Ladungen, erhält man nach­folgendes Diagramm:

Diagramm (wird später eingefügt)

Der Verlauf einer solchen gleich­namigen Probe­ladung verläuft hyper­bolisch, proportional zu 1 /R.

Betrachtet man dagegen ungleichnamige Ladungen, erhält man nach­folgendes Diagramm:

Diagramm (wird später eingefügt)

Der Verlauf einer solchen ungleichnamigen Probeladung verläuft auch hyper­bolisch, aber proportional zu −1 /R. Bei herannahen an die Ladung, wird die potentielle Energie immer kleiner und die Ladungen ziehen sich immer stärker an. Hier spricht man auch von einer Potential­mulde. Man erkennt sehr schön die hyper­bolischen Abhängig­keiten der poten­tiellen Energie vom Abstand.

Nun definieren wir uns eine Größe, die uns durch die ganze Elektro­dynamik hindurch begleiten wird. Und zwar die „elektrische Spannung”.

Wenn man ein elektrisches Feld hat, das kann zum Beispiel ein Feld einer Punkt­ladung sein oder irgendein anderes Feld im inneren eines Konden­sators, dann ist es oft sinnvoll, zwei Punkte darin zu betrachten. An einem der beiden Punkte befindet sich die Probe­ladung q. Jetzt geht es darum, welche Arbeit verrichtet werden muss, um diese Probe­ladung von einem Punkt zum anderen Punkt zu bewegen. Denn das ist eine wichtige Größe zur Beschreibung des elektri­schen Feldes. Daher nennt man die Arbeit, bezogen auf die Ladungs­einheit, die „elektrische Spannung”.

Die elektrische Spannung U zwischen zwei Punkten ist definiert als:

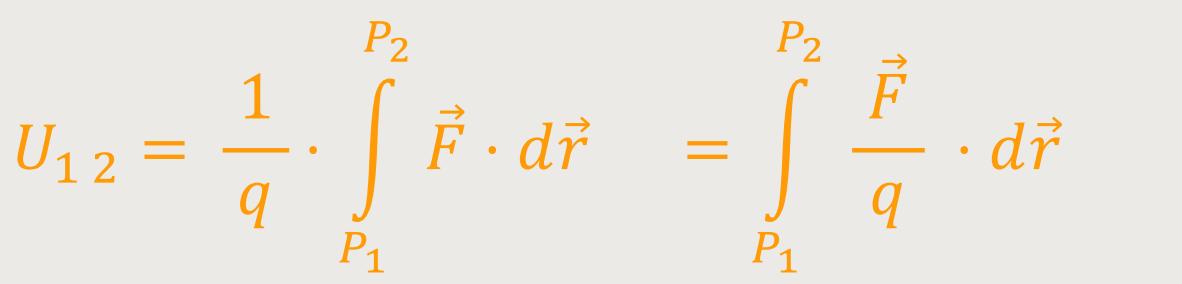
Da die Probeladung konstant ist, kann man sie in das Integral hinein­ziehen, und man bezieht sich damit auf die elektrische Feld­stärke:

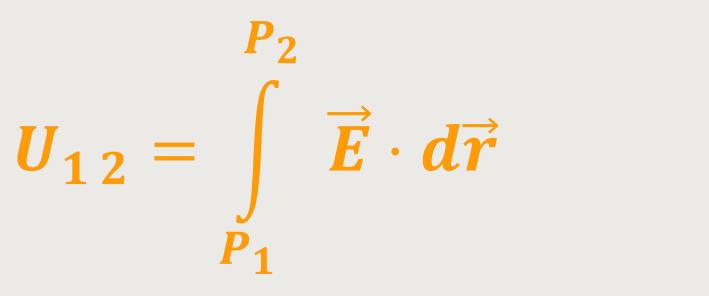
Die elektrische Spannung ist die Arbeit, die in einem elektrischen Feld verrichtet wird, wenn man die Ladung von einem Punkt zu einem anderen bewegt, und zwar pro Ladungs­einheit. Damit ist die Feld­stärke die Kraft pro Ladungseinheit.

Um das jetzt aus Sicht der Elektrostatik umformen zu können, muss man auch die potentielle Energie V auf die Ladungs­einheit beziehen. Und das nennt man dann das „elektrische Potential”.

Das „elektrische Potential” ist dann nichts anderes als die potentielle Energie pro Ladungseinheit:

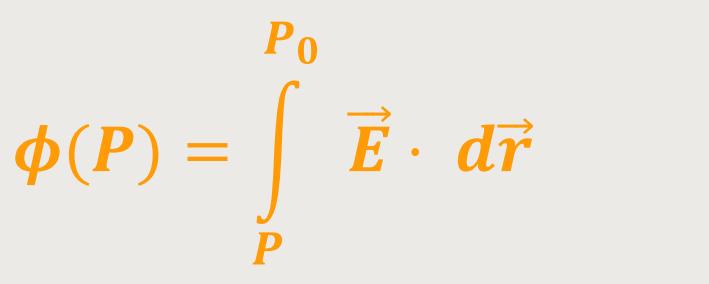
Was bedeutet das? Wenn man sich in einem konser­vativen elektrischen Feld befindet, wie das beispiels­weise in der Elektro­statik der Fall ist, dann erhält man damit einen Ausdruck für die Spannung. Doch zunächst nochmals die Definition die immer gilt, auch für nicht konser­vative elektrische Felder (siehe oben):

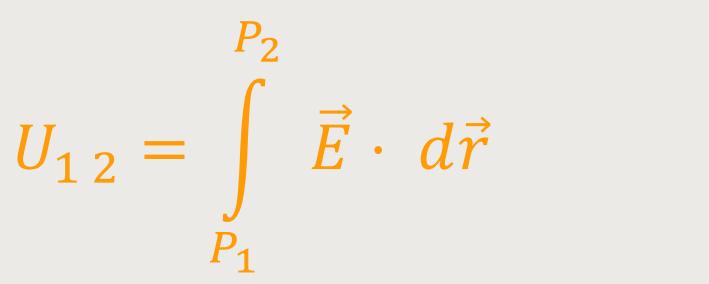
Um dieses Intergral umformen zu können, muss man es zunächst anders aufschreiben.

Grafik (wird später eingefügt)

Da es bei konservativen elektrischen Feldern keine Rolle spielt, auf welchem Weg man beide Punkt miteinander verbindet, kann man auch einen Umweg über P₀ wählen. Dann sieht das Integral wie folgt aus:

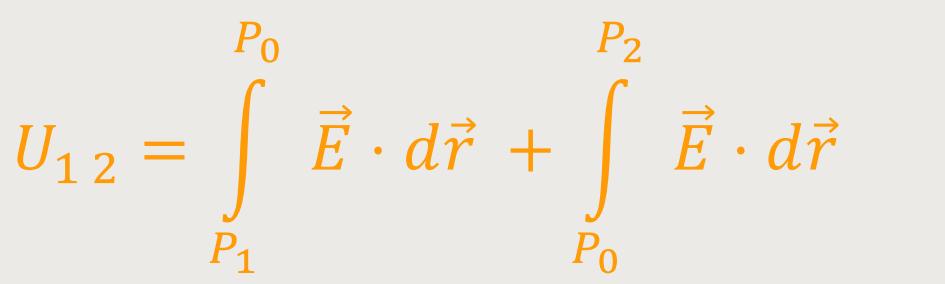
Wenn man nun entsprechend einsetzt, und ein Vertauschen der Grenzen im Integral vornimmt, erhält man:

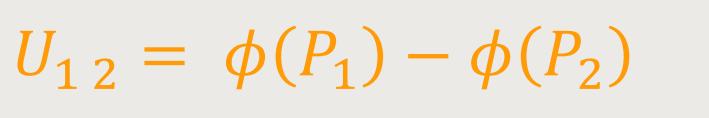
Somit ist die Spannung eine Potential­differenz zwischen zwei Punkten bzw. die Differenz der Potential­werte in diesen beiden Punkten. Das gilt aber nur für konservative elektrische Felder.

Bei Induktions­vorgängen mit zeit­abhängigen elektrischen und magne­tischen Feldern ist das nicht mehr der Fall. Dort treten nämlich elektrische Wirbel­felder auf. Dann lässt sich das nicht mehr als Potential­differenz darstellen. In einem Wirbel­feld ist eine potentielle Energie nicht definierbar.

Die Einheit für die Spannung ist:

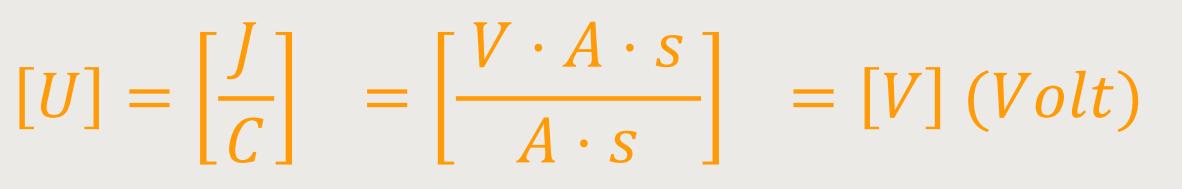
Die ganzen vorgenannten Überlegungen dienen letztlich dazu, die Maxwell-Gleichung lösen zu können.

Aber zuvor muss man noch einen Zusammen­hang herstellen, zwischen der Feld­stärke und dem Potential. Da gibt es nämlich noch eine einfachere Vorgehens­weise, elektrische Felder zu beschreiben.

Aus der Mechanik weiß man, dass die Kraft gleich dem negativen Gradienten der potentiellen Energie ist:

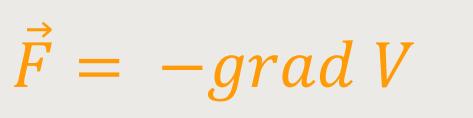
Nun kann man beide Seiten auf die Ladungs­einheit beziehen. Kraft pro Ladungs­einheit ist die „elektrische Feld­stärke”. Potentielle Energie pro Ladungs­einheit ist das „elektrische Potential”:

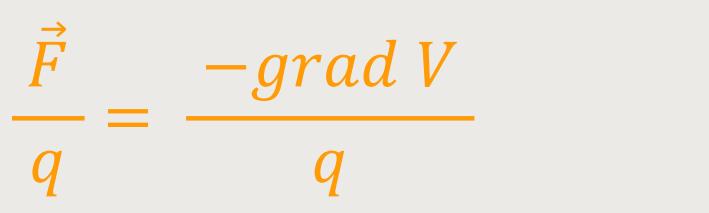
Daraus folgt:

Wenn man also ein elektro­statisches Feld betrachtet, benötigt man drei Komponenten der elektrischen Feld­stärke als Orts­funktion. Wenn diese bekannt sind, lässt sich das entsprechende Potential ermitteln. Und daraus ergibt sich, dass man nur noch eine skalare Funktion (Größe) als Orts­funktion kennen muss. Und wenn man dann den Gradienten bildet, erhält man das gesamte elektrische Feld.

Damit benötigt man nicht mehr ein ganzes Vektor­feld zu Ermittlung der elektrischen Feld­stärke, sondern es reicht schon ein skalares Feld aus.

Die Einheit für die elektrische Feldstärke ist:

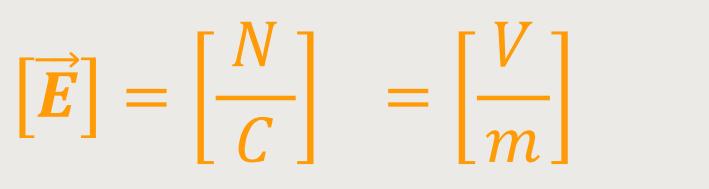
Hinweis: Bei der Einheit schreibt man die Längen­einheit m, weil der Gradient nach einer Längen­größe differenziert wird.

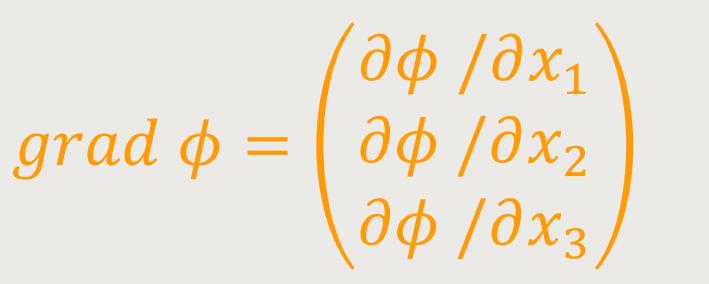
Wenn man das ϕ (phi) als Orts­funktion kennt, erstellt man die drei partiellen Ableitungen, und erhält damit die drei Komponenten des Gradienten. Und −grad (s.o.) ist dann bereits der elektrische Feldstärke­vektor.

Das Potential ϕ hängt natürlich von der Wahl des entsprechenden Bezugs­punktes ab. Denn wenn man den Bezugs­punkt ändert, verändert sich auch die potentielle Energie oder allgemein das Potential um einen festen, konstanten Betrag. Das hat aber auf den Gradienten keine Auswirkungen. Denn da geht es nur um die Ableitungen nach den Orts­koordinaten. Wenn sich das Potential ϕ um einen konstanten Term verändert, fällt dieser beim Differen­zieren weg, und das entspricht dann dem Wert Null, und daher ändert das nichts an der elektrischen Feldstärke.

Wenn man das jetzt zum Beispiel auf das Feld einer Ladung Q (Spezialfall) anwendet, dann ergibt sich:

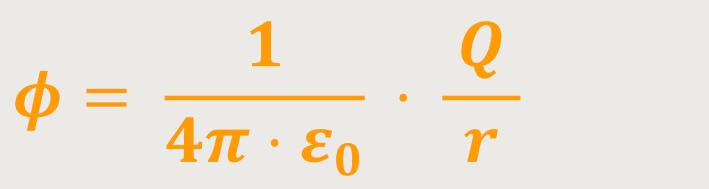
Auch hier liegt der Bezugspunkt im Unendlichen. Denn wenn man mit dem Abstand r Richtung unendlich geht, dann geht auch das Potential gegen Null .

Dement­sprechend erhält man einen Ausdruck für die Spannung zwischen zwei Punkten in einem elek­trischen Feld der Ladung Q bezüglich obiger Spannungs­definition:

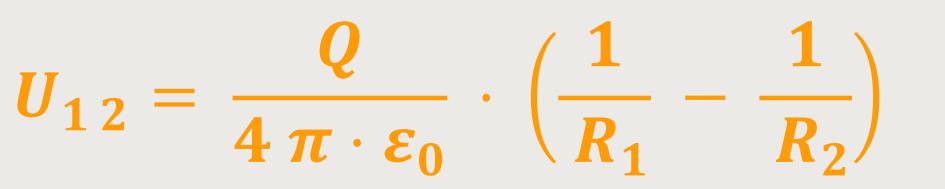
Und damit erhält man eine leicht anwendbare Formel. Es kommt somit letztlich nur noch auf die Abstände der Punkte im Feld der Punktladung an.

Was heißt das konkret für die Maxwell-Gleichung? Wenn man das grad ϕ entsprechend einsetzt, erhält man:

Was ist aber die Divergenz eines Gradienten? Nun, der Gradient bezieht sich hier auf eine skalare Größe. Daraus ergibt sich ein Vektor. Und die Divergenz bezieht sich wiederum auf ein Vektor­feld. Und daraus wird wieder ein Skalar.

Wenn man das ausrechnet, erhält man:

Und das ist nichts anderes als der „Laplace-Operator” in drei Dimensionen:

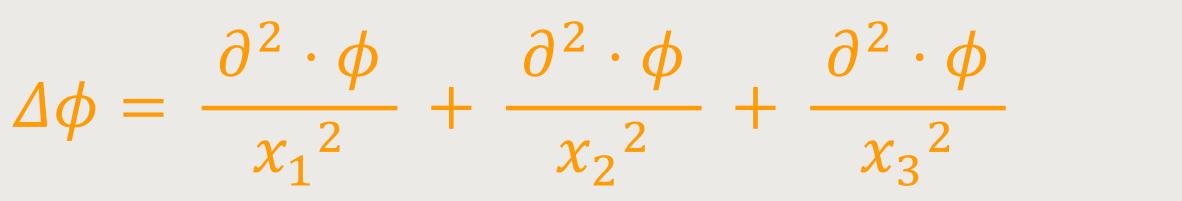
Und damit erhält man zusammenfassend die sogenannte „Poisson-Gleichung”:

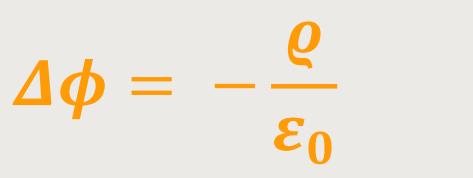
Das ist eine ganz wichtige Grund­gleichung der Elektrostatik.

Diese Gleichung hat einen großen Vorteil gegenüber der Maxwell-Gleichung. Das gilt zwar zunächst alles nur dort, wo man einfache skalare Potentiale einführen kann. Und zusätzlich muss man ein konser­vatives elektrisches Feld voraus­setzen. Aber diese Gleichung ermöglicht es, bei vorgegebenen Ladungs­dichten eine skalare Orts­funktion als Lösung zu ermitteln.

Man kann jetzt für die unterschied­lichsten Anfangs­bedingungen und Ladungs­verteilungen die zugehörigen Potentiale ausrechnen. Anschließend benötigt man nur noch den Gradienten von dem jeweiligen Potential, und man erhält bereits die elektrische Feld­stärke für die jeweilige Situation.

Und wenn man einen ladungsfreien Raum hat, schrumpft die Grundgleichung auf die „Laplace-Gleichung” zusammen:

Nach dieser Gleichung ist obiger Laplace-Operator bezeichnet worden. Beide Gleichungen sind die Grund­gleichungen in der Elektrostatik.

Ein elektrisches Feld einer einzelnen positiven Ladung stellt sich wie folgt dar:

Grafik (wird später eingefügt)

Man sieht die radial nach außen laufenden Feldlinien und bei einer positiven Ladung sind die Feldstärke­vektoren nach außen gerichtet. Die konzen­trischen Kugeln (gestrichelt) sind sogenannte Äquipotential­flächen in der Umgebung einer solchen feld­erzeugenden Punkt­ladung. Denn das Potential ist nur vom Abstand r abhängig. Man spricht auch von Niveau­flächen des elektrischen Potentials.

Das gleiche gilt auch für eine negative Ladung, nur dass die Feld­stärke­vektoren jetzt nach innen gerichtet sind.

Grafik (wird später eingefügt)

Bei entgegengesetzten gleichgroßen Ladungen wird das ganze schon etwas komplizierter:

Grafik (wird später eingefügt)

Wegen der Linearität der Grund­gleichungen werden sich bei mehr Ladungen die Felder über­lagern. Und wenn man dann einen Feld­anteil von der einen Ladung und von der anderen Ladung auf eine Probe­ladung hat, dann wird die Vektor­summe zur Gesamt­summe der Kraft pro Ladungs­einheit und damit der elektrischen Feldstärke.

Die Feldlinien sind als Tangentialkurven an die Feld­stärke­vektoren eingetragen. Und die Äquipotential­flächen verlagern sich etwas bzw. sind nicht mehr konzentrisch, sondern seitlich verschoben.

Als letztes Beispiel sehen wir zwei gleich große positive Punktladungen:

Grafik (wird später eingefügt)

Die Feldlinien stoßen sich jetzt gegen­seitig ab. Und die Äquipotential­flächen bilden sich zu einer Schleife (∞) aus. Doch im Allgemeinen hat man es mit vielen Ladungen zu.

Bei einem System bestehend aus vielen Ladungen, kann man das Potential für eine Ladungs­wolke aus vielen einzelnen Punkt­ladungen einfach als Summe über lauter Potentiale von den einzelnen Ladungen aufschreiben:

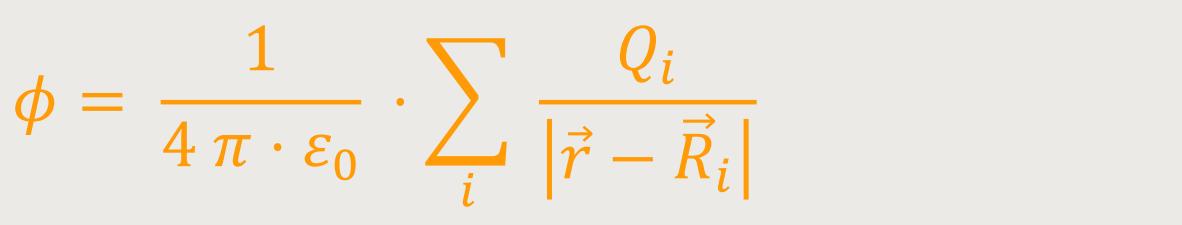
In diesem Fall muss man über alle Ladungen Q aufsummieren. Und man erhält dann eine Summe über das ganze Volumen V. Zusätz­lich wird durch den Abstands­vektor am Punkt P dividiert. Das ist im Wesent­lichen nichts anderes als der Betrag zwischen dem Ortvektor des Punktes P und den Orts­vektoren der einzelnen Ladungen.

Mit einer derartigen Darstellung kann man grund­sätzlich auf der Basis der Poisson-Gleichung auch Felder von ganz allgemeinen Ladungs­verteilungen berechnen.

⇦ Kapitel Kapitel ⇨