Das Coulomb-Gesetz besagt, dass die Kraft zwischen zwei Punkt­ladungen gegeben ist durch einen Vorfaktor und den beiden entspre­chenden Ladungen:

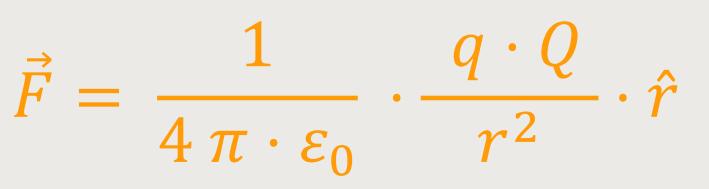
ist ein Einheitsvektor der Länge 1

Dieser Einheitsvektor ist von der einen zu der anderen Ladung gerichtet. Die Kraft­wirkung verläuft längs dieses Vektors.

Die Ladung Q erregt den sie umschlie­ßenden Raum, also ein Feld, und die Ladung Q, die sich unter der Wirkung dieser Ladung Q befindet. Auf diese zweite Ladung wird somit eine Kraft ausgeübt. Ist die Kraft positiv, so ist der Kraft­vektor auf die Probe­ladung Q nach außen gerichtet. Es hängt natürlich von der Größe der Punkt­ladungen ab, wie groß letztlich diese Kräfte sind.

Die Kraftwirkung ist linear abhängig von der Größe der jeweiligen Probe­ladung Q, die sich in der Umgebung der feld­erzeugenden Ladung Q befindet. Daher ist es möglich, das elektrische Feld in der Umgebung einer Ladung Q zu charakte­risieren. Und zwar geschieht das mittels der Kraft, die auf die Ladungs­einheit wirkt. Und diese Kraft nennt man dann die „elektrische Feld­stärke”:

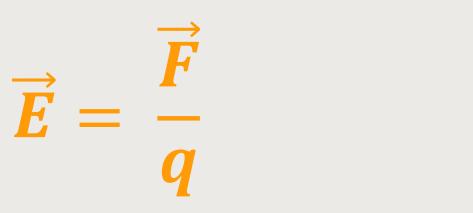
Dabei spielt es keine Rolle, um welches elektrische Feld es sich handelt. Das heißt, egal ob es das Feld einer Punkt­ladung ist oder das Feld im Innern eines Platten­kondensators. Man erhält die Größe der Feld­stärke in einem gewissen Punkt in diesem elektrischen Feld, indem man eine gewisse Probe­ladung oder Punkt­ladung Q an die zu betrachtende Stelle setzt. Anschließend wird gemessen, wie groß die mechanische Kraft­wirkung auf diese Punkt­ladung ist, und dividiert diese Kraft durch die Größe dieser betrachteten Punktladung.

Im Bereich der Elektro­statik üben die Ladungen auf sich selbst keine Kraft aus. Deshalb muss bei der Ermittlung der Gesamt­kraft das Feld der jeweiligen Probe­ladungen Q nicht berück­sichtigt werden. Wenn die feld­erzeugende Ladung Q positiv ist, dann zeigen alle Feld­vektoren von der Ladung weg. Wenn die Ladung dagegen negativ ist, sind die Feld­vektoren alle zur Ladung Q hin gerichtet.

Jedes Vektorfeld kann man durch Feld­linien beschreiben, die radial von der feld­erzeugenden Ladung nach außen gerichtet sind. Die Feld­linien sind dann die Tangential­kurven an den Feldstärkevektor.

In der Hydrodynamik wird der Volumen­fluss eines Fluids über eine Querschnitts­fläche berechnet.

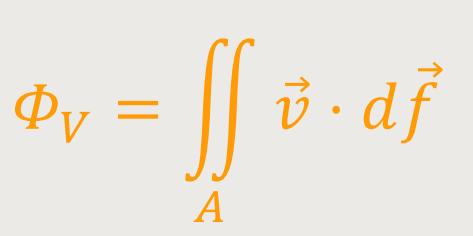
Analog dazu lässt sich der elektrische Fluss definieren:

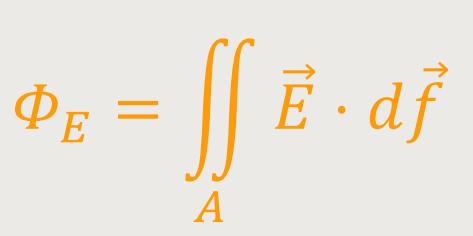
Hierbei ist allerdings zu berück­sichtigen, dass die Feldstärke­vektoren eine ganz andere physika­lische Bedeutung haben als die Geschwindig­keits­vektoren . Denn die Feld­stärke­vektoren sind eng verbunden mit den Kraft­vektoren. Da fließt nichts im eigentlichen Sinne.

Die Feldstärke in der Umgebung einer Punktladung kann definiert werden als:

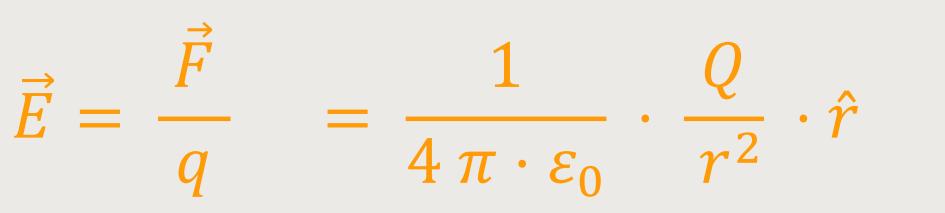
Um nun den elektrischen Fluss ermitteln zu können, denkt man sich rund um die feld­erzeugende Ladung eine konzen­trische Kugel­oberfläche mit einem Radius R.

Daraus ergibt sich jetzt ein Ring­integral rund um diese Ladung herum. Dement­sprechend lässt sich der elektrische Fluss definieren als Flächen­intergral:

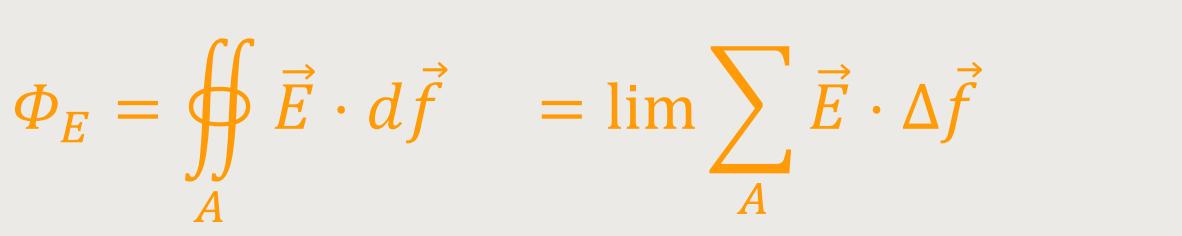
Für · Δ kann man auch schreiben || · Δ f. Und da der Betrag von konstant bleibt, weil der Radius der Kugel­fläche immer konstant ist, kann man somit verkürzt schreiben:

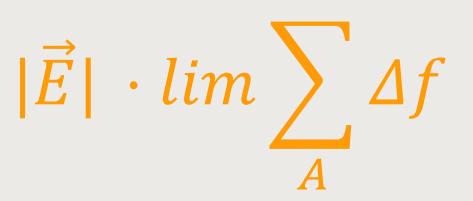
Wenn man für || obige Definition einsetzt, und dabei berücksichtigt, das lim Σ_A Δ f der Kugel­oberfläche entspricht, kann man auch schreiben:

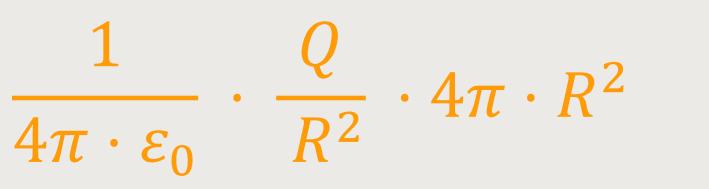
Und damit bleibt nach Wegkürzen nur noch stehen:

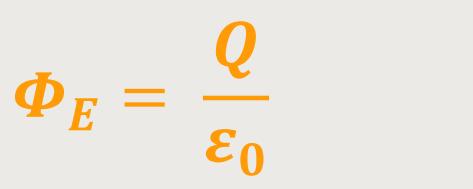
Diese Beziehung wird auch als das Gauß'sche Gesetz bezeichnet, welches ein physika­lisches Grund­gesetz der Elektrostatik ist.

Mit diesem Gesetz wird deutlich, dass der elektrische Fluss nicht von der Größe der Kugel­fläche abhängig ist. Wenn man nämlich nicht nur „eine” Punkt­ladung, sondern eine „ganze Wolke” von Punkt­ladungen (Ladungs­dichte­verteilungen) betrachtet, die zudem nicht von einer Kugel­fläche, sondern von einer beliebig geformten Fläche umschlossen ist, bleibt dieses Gesetz trotzdem bestehen.

Bei dem elektrischen Fluss ist es allerdings immer wichtig zu charakte­risieren, durch welche geschlossene Fläche dieser Fluss tritt. Dieses Φ_E ist der gesamte elektrische Fluss des Feldes der Ladungs­wolke durch eine geschlossene Oberfläche hindurch.

Wenn der elektrische Fluss positiv ist, und somit von der feld­umschlossenen Ladung weggerichtet ist, spricht man von Quellen, wenn er dagegen negativ ist, und damit in Richtung der Ladung zeigt, spricht man von Senken.

Wie lässt sich nun diese räumlich ausgedehnte Ladungs­verteilung in einem Volumen V betrachten?

Ein gegebenes Volumen kann mit einer Ladungs­dichte ρ (rho) beschrieben werden. Die Ladungs­dichte ist eine skalare Funktion, die ortabhängig ist. Sie wird definiert als:

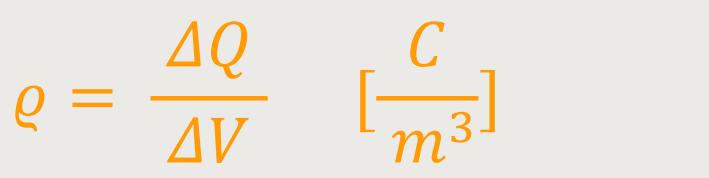
Damit erhält man für die Gesamtladung:

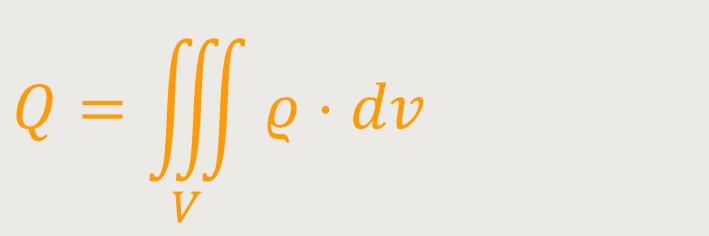
Wenn man diese Beziehung jetzt in das Gauß'sche Gesetz einsetzt, erhält man:

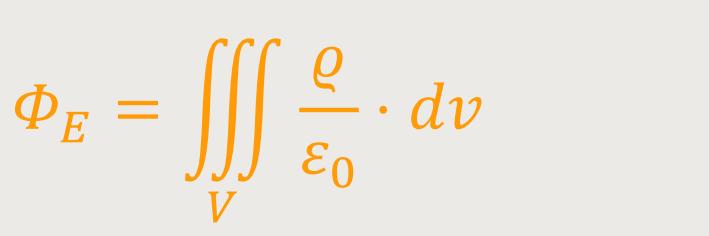
Bezogen auf die Definition des elektrischen Flusses bedeutet das wiederum:

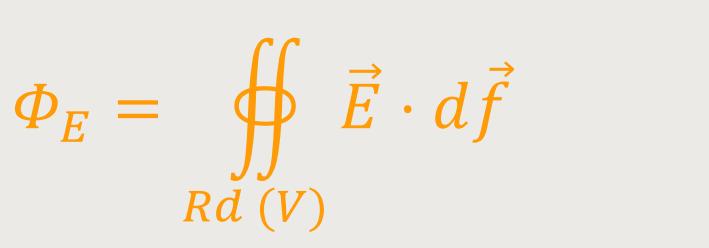
Da es sich hierbei um eine geschlossene Fläche handelt, bezieht man sich hier entsprechend auf den Rand Rd des Volumens V .

Das Integral über ein Volumen von einer Größe „Divergenz”, ist gleich dem Flächen­intergral über den Rand des betrachteten Volumens:

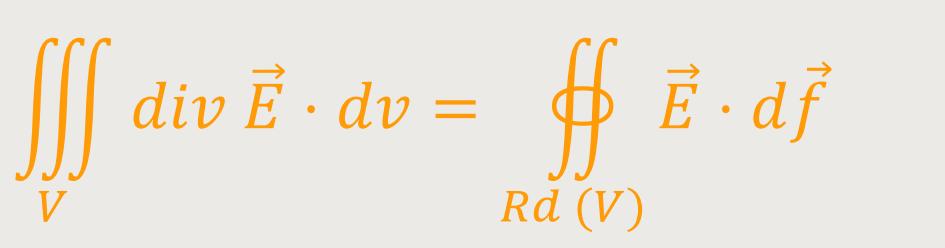
Wobei die Divergenz gegeben ist als:

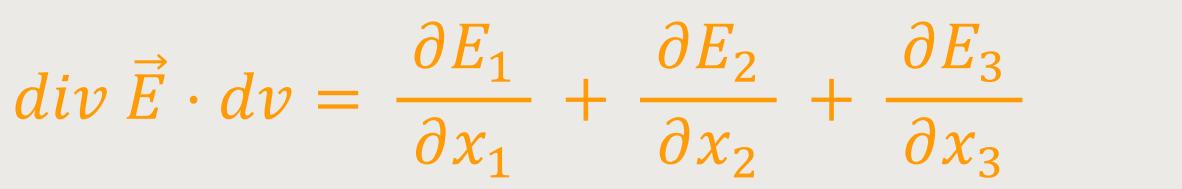
Wenn man jetzt das Volumen­integral mittels des Gauß'schen Integral­satzes umformt, ergibt sich für den elektrischen Fluss:

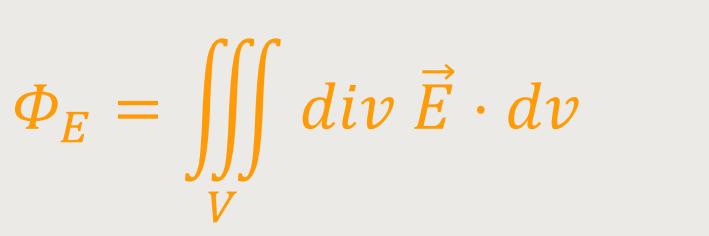
Werden abschließend beide zuvor erarbeiteten Beziehungen für den elektrischen Fluss gleichgesetzt, erhält man:

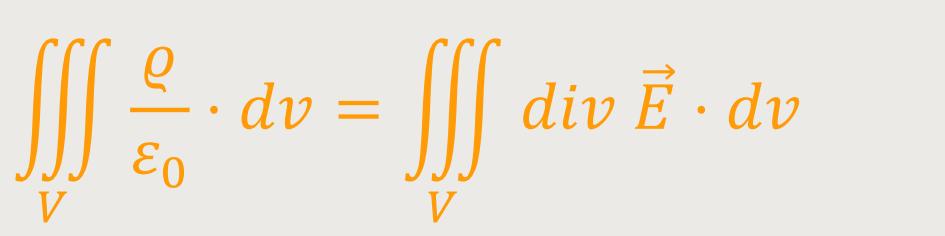
Diese Gleichung ist dann erfüllt, wenn die Integranden das Gleiche aussagen. Und wenn die Gleichung für beliebige Volumen erfüllt sein soll, gilt das auch nur bei gleichen Integranden. Dement­sprechend ergibt sich eine wichtige Beziehung:

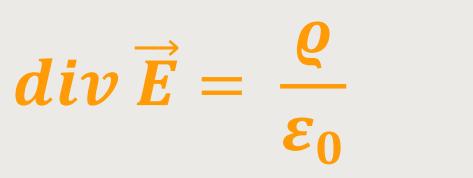
Und damit erhält man die „erste” der vier Maxwell-Gleichungen. Oft auch geschrieben als:

Was versteht man also unter der Divergenz?

Für obige Über­legungen wollen wir hierzu ein kleines Volumen ΔV betrachten. Klein bedeutet in diesem Fall, das sich über den Bereich des Volumens der jeweils betrachtete elektrische Feld­vektor nicht gravierend ändert. In einem solchen Fall lässt sich obiges Ringintegral umformen.

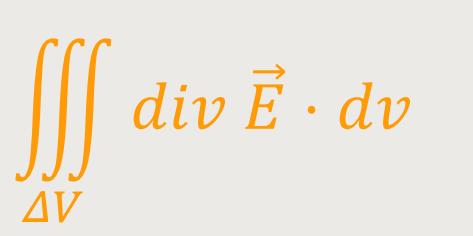
Dieses Volumenintegral ist ja zunächst nichts anderes, als eine Summe über alle ΔV. Und jetzt soll das einzelne ΔV klein genug sein, sodass man gar keine Volumen­würfel mehr benötigt. Das bedeutet letztlich, dass die Divergenz im Wesent­lichen konstant bleibt. Somit lässt sich jetzt die Divergenz vor das Integral schreiben:

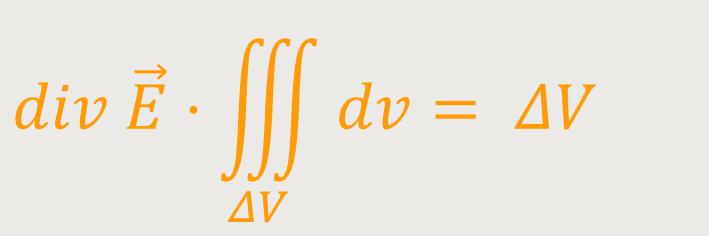
Und damit gilt für das Ring­integral unter Berück­sichtigung nur „eines” Volumenwürfels:

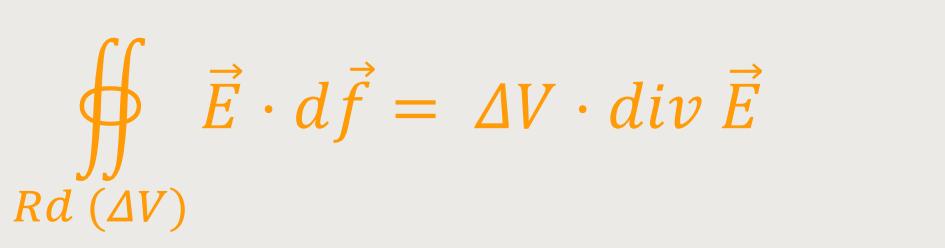
Durch Umformung erhält man für die Divergenz:

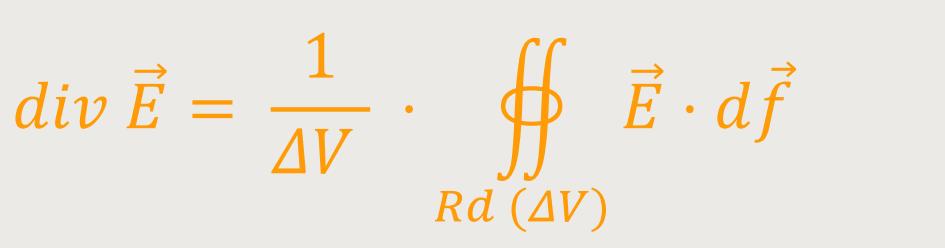
Die Divergenz in diesem kleinen Volumen ist jetzt nichts anderes als der Fluss des elektri­schen Feldes aus dem kleinen Volumen heraus, sprich durch die Rand­fläche des Volumens hindurch. Also der elektrische Fluss · d pro Volumen­einheit ΔV. Wenn man im Limes (Grenzwert) dieses Volumens immer kleiner wird, kommt man im Grenzwert auf die div als Punkt­funktion. Und dieser Fluss pro Volumen­einheit wird als „Quelldichte” bezeichnet.

Und damit sagt die Maxwell-Gleichung etwas ganz einfaches aus:

Die Ladungsdichte ist gleich die Quell­dichte des elektrischen Feldes.

Wo keine Ladungen vorhanden sind, gibt es demnach auch keine Quellen des elektrischen Feldes.

⇦ Kapitel Kapitel ⇨