Wie wir gesehen haben, führt das Vorhandensein von nicht­leitenden Medien in einem elektrischen Feld zu Verände­rungen. Aufgrund der Dipoleigen­schaften der Moleküle richten sich diese, unter der Einwirkung eines äußeren elektrischen Feldes, entsprechend aus.

Durch das dielektrische Medium wird die elektrische Feldstärke um einen gewissen Faktor reduziert. Wobei die Größe dieses Faktors je nach Medium sehr unterschiedlich ist.

Nachfolgend sind einige dieser relativen Dielektrizitäts­konstanten, um die das Feld reduziert wird, aufgeführt:

Tabelle (wird später eingefügt)

Somit hat die Anwesenheit von Luft zwischen den Kondensator­platten praktisch keine Auswirkungen. Diese Werte sind einerseits temperatur­abhängig und vor allem frequenz­abhängig. Wenn man im Gegensatz dazu elektro­magnetische Felder betrachtet, können diese Werte erheblich voneinander abweichen. Da wir uns noch in der Elektro­statik bewegen, sind das alles natürlich statische Werte.

Bei dem Platten­kondensator wurde nicht primär das Feld gemessen, sondern die elektrische Spannung. Bei der Herstellung von Kondensatoren, in denen Materialien mit einer hohen Dielektrizitäts­konstante verbaut sind, entspricht das dem Faktor, um den die Kapazität größer wird. Und wenn man zusätzlich die Distanz zwischen den Platten möglichst klein hält, wird die Kapazität zusätzlich erhöht.

Jetzt werden wir uns konkret den „freien Ladungen” zuwenden.

Wir gehen also zunächst von einem elektrischen Feld aus, in welchem sich ein materielles dielektrisches Medium befindet.

Anfänglich betrachtet man die Situation so, als gäbe es in dem System kein Dielektrikum. Damit bleiben die Polarisations­ladungen vorerst außen vor, und wir betrachten nur die freien Ladungen. Dies sind in unserem Beispiel die Ladungen auf den Kondensator­platten. Wir blenden das Dielektrikum quasi einfach aus.

Für den Vakuum-Kondensator gilt dann die „erste” der vier Maxwell-Gleichungen:

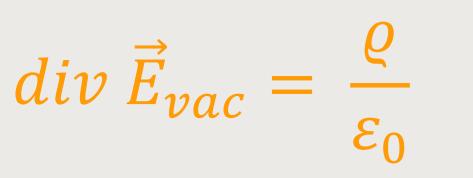
ϱ   ist die Dichte der freien Ladungen

Damit man aber nicht immer _vac hinschreiben muss, definiert man sich einen weiteren Feldvektor neben dem , nämlich . Unter diesem Vektor versteht man die „dielektrische Verschiebung”. Wenn man von der dielektri­schen Verschiebung spricht, ist damit das Durch­treten von elektrischen Feldern durch Grenzflächen gemeint.

Die rein formale Definition lautet:

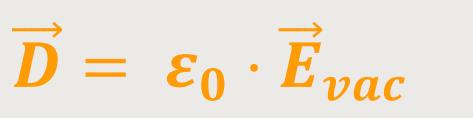
Es handelt sich hierbei um einen Repräsentanten des Vakuumfeldes.

Wenn man jetzt obige Maxwell-Gleichung umstellt und entsprechend einsetzt, ergibt sich:

Somit rührt die dielektrische Verschiebung von den freien Ladungen her. Die freien Ladungen sind somit die Quellen der dielektrischen Verschiebung.

Jetzt blenden wir das Dielektrikum wieder ein. Aufgrund der Polarisations­ladungen ist das Feld um den Faktor ε_r kleiner als im Vakuum:

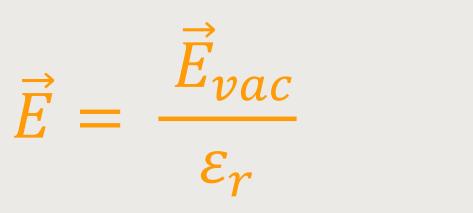
Weil das Vakuumfeld repräsentiert, bleibt die dielektrische Verschiebung unverändert. Und daraus ergibt sich folgender Zusammenhang:

ε_₀   ist elektrische Feldkonstante
ε_r   ist die relative Dielektrizitätskonstante

Und das nennt man der Einfachheit halber verkürzt:

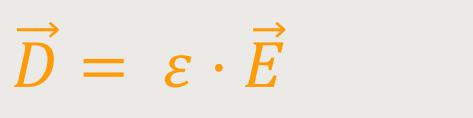
Damit entspricht diese Gleichung jetzt einer Material­gleichung.

ε   ist allgemein die Dielektrizitäts­konstante

Warum geht man so vor?

Da als Repräsentant des Vakuum­feldes immer unverändert bleibt, spielt es keine Rolle ob ein Medium vorhanden ist oder nicht. Möchte man aber die elektrische Feld­stärke ausrechnen, benötigt man grundsätzlich eine Material­gleichung. Allerdings müssen hierbei zunächst die Polarisations­ladungen nicht explizit betrachtet werden.

Wenn nun aber keine freien Ladungen vorhanden sind, also ϱ = 0 dann gilt:

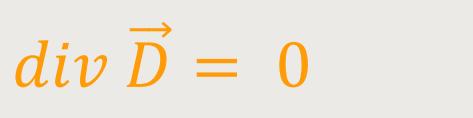
In diesem Fall ist das Feld „quellfrei”. Damit gilt zwangsläufig:

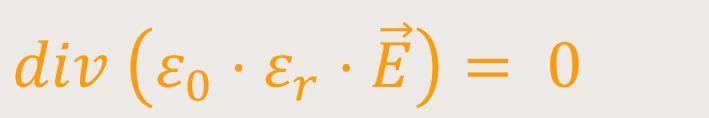
Das trifft allerdings nur dann zu, wenn ein homogenes Medium vorhanden ist.

Wenn dagegen eine Grenz­fläche vorhanden ist, wird die relative Dielektrizitäts­konstante ε_r raumabhängig bzw. ortsabhängig sein. Und dann gilt für ein inhomogenes Medium:

Damit ergibt sich allgemein für vorhandene Grenzflächen:

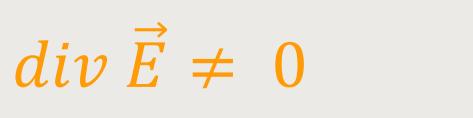
Und das bedeutet wiederum, dass es in dem System Bereiche gibt, bei denen die -Linien entspringen oder enden, und zwar dort, wo sich die Polarisations­ladungen befinden.

Was ist zu beobachten, wenn man Felder betrachtet, die durch ebene Grenz­flächen, bestehend aus verschiedenen Dielektrika, hindurch­treten? Also wenn diese hinter­einander angeordnet sind. Und was für Bedingungen gibt es an „ebenen” Grenz­flächen? Hierzu betrachten wir zwei Fälle.

Im ersten Fall soll die Feldrichtung „senkrecht” zur Grenz­fläche verlaufen. Es wird zwar wieder Polarisations­ladungen geben, aber es seien dort keine freien Ladungen in der Grenzfläche vorhanden.

Dann ergibt sich:

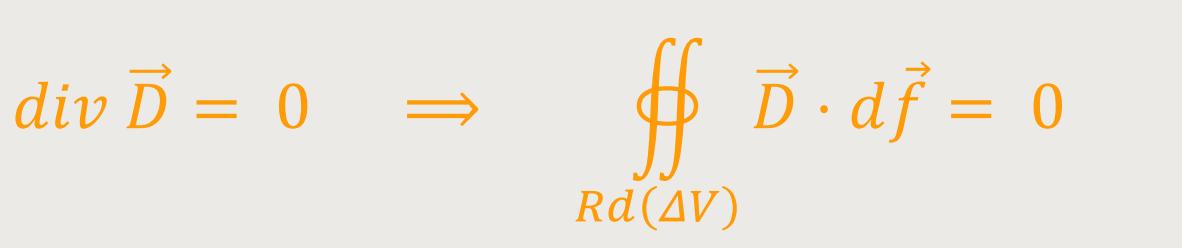
Somit ist der elektrische Fluss aus einer geschlossenen Fläche heraus gleich Null.

Grafik (wird später eingefügt)

Wenn man seitlich auf eine solche Grenz­fläche draufschaut, dann gibt es zum Beispiel oberhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₁, und unterhalb sei ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₂. Nun betrachten wir an der Grenz­fläche einen kleinen Zylinder, der die Grenz­fläche durch­dringt. Dann wird in diesem Fall ein senkrecht von oben auf die Zylinder­fläche auftreffen und unten wieder heraus­treten. Von der Deck­fläche des Zylinders weg wirkt zusätzlich entgegen­gesetzt ein Flächen­vektor d₁ und von der Boden­fläche weg ein weiterer Flächen­vektor d₂. Dann ist −d₁ = d₂. Laut Definition ist der Fluss aus so einem kleinen Zylinder­volumen heraus immer Null.

Demnach gilt folgende Beziehung:

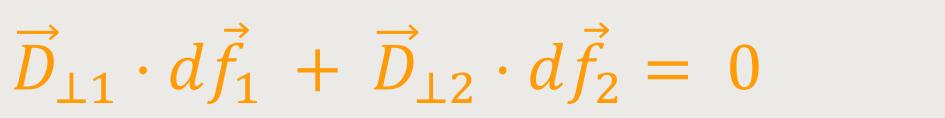
Daraus ergibt sich:

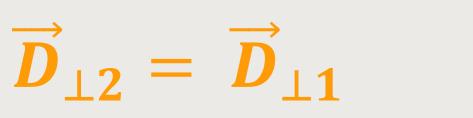
Der Verschiebungsvektor wird sich nicht ändern, wenn das elektrische Feld senkrecht zur Grenz­fläche liegt. Somit ist die Normal­komponente der dielektrischen Verschiebung durch eine Grenz­fläche hindurch stetig, also sie ändert sich nicht.

Das bedeutet für das elektrische Feld und deren Feldkonstanten:

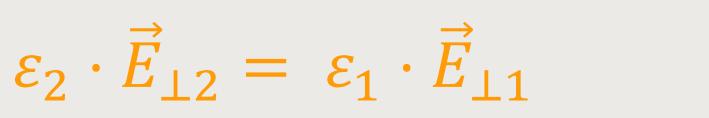
Nach Umformung erhält man:

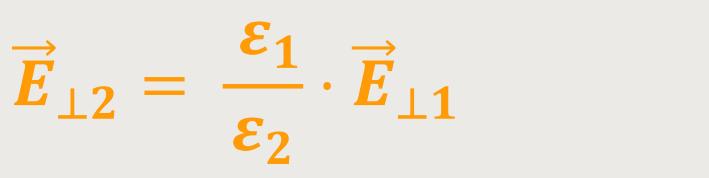
Also, das elektrische Feld ändert sich, während die dielektrische Verschiebung unverändert bleibt.

Im zweiten Fall, den wir betrachten, verläuft die Feld­richtung „parallel” zur Grenz­fläche.

Hier kann man voraussetzen, dass das elektrische Feld statisch ist und damit konservativ. Daher gilt für das Ringintegral:

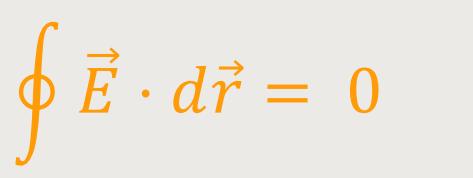
Grafik (wird später eingefügt)

Wir schauen wieder seitlich auf die Grenz­fläche, bei der sich oberhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₁ befindet, und unterhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₂. Nun betrachten wir an der Grenz­fläche eine geschlossene Kurve, welche die Form eines flachen Rechtsecks darstellt, und die Grenz­fläche durch­dringt. In diesem Fall verlaufen die elektrischen Felder oberhalb und unterhalb der Grenz­fläche parallel zu dieser Grenz­fläche. Die Flächen­vektoren verlaufen auch entsprechend parallel, wobei der Flächen­vektor d₁ oberhalb der Grenz­fläche gleich­gerichtet mit dem elektrischen Feld verläuft, und der Flächen­vektor d₂ unterhalb der Grenz­fläche entgegen­gesetzt zum elektrischen Feld.

Damit werden sich die Flächen­vektoren −d₁ = d₂ wieder aufheben. Wegen der Konservativität des elektrischen Feldes ist das Linien­integral immer Null. Das bedeutet für das Linien­integral:

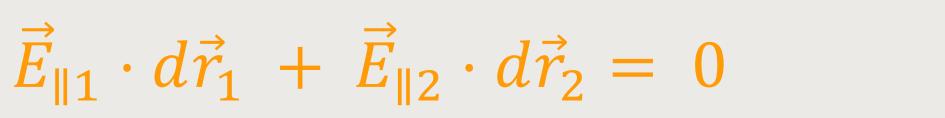
Daraus ergibt sich letztlich:

Hier ist jetzt die Parallel­komponente des elektrischen Feldes, sprich des Feldstärke­vektors, längs einer Grenz­fläche „stetig”, also sie ändert sich nicht.

Das bedeutet für die dielektrische Verschiebung :

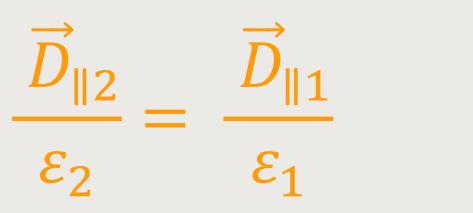
Nach Umformung erhält man:

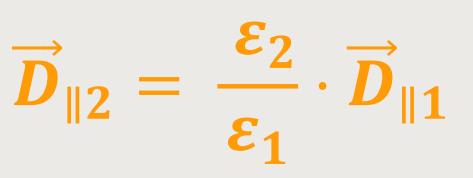
Hier ist die dielektrische Verschiebung „nicht stetig”.

Hier haben wir also zwei unterschied­liche Verhaltens­weisen bei elektrischen Feldern an der ebenen Grenz­fläche von zwei beieinander liegenden Dielektrika betrachtet.

Übertragen wir diese Überlegungen nochmals auf unseren Platten­kondensator.

Grafik (wird später eingefügt)

Das -Feld mit seiner dielektrischen Verschiebung hat seine Quellen nur in den „freien” Ladungen. Die Polarisations­ladungen führen dazu, dass das elektrische Feld zum Teil im Dielektrikum endet und nur teilweise wieder entspringt bzw. heraustritt.

Im dritten und letzten Fall liegt das Feld schräg zur Grenzfläche.

Grafik (wird später eingefügt)

Auch hier schauen wir wieder seitlich auf die Grenz­fläche, bei der sich oberhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₁ befindet, und unter­halb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₂. Die dielektrischen Verschiebungs­vektoren stehen wieder senkrecht auf die Grenz­fläche und gleichen sich im Betrag. Aber die parallel verlaufenden Verschiebungs­vektoren können durchaus verschiedene Beträge aufweisen. Dadurch kommt es zu einer Brechung der Feldlinien mit unterschied­lichen Brechungswinkeln.

Für die -Linien bedeutet das:

Das Verhältnis stellt sich dann wie folgt dar:

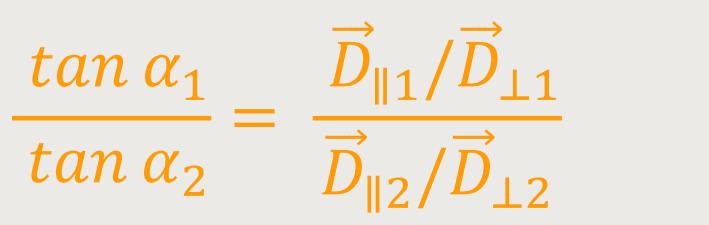
Da die Normalkomponenten von aber stetig sind, fallen diese weg, und es bleibt nur noch stehen:

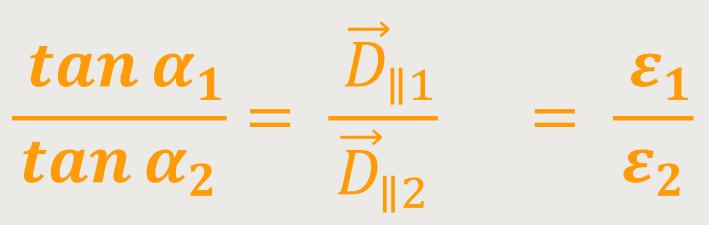
Und das ist das Brechungsgesetz für die -Linien.

Im Gegensatz dazu sieht die Beziehung für die -Linien etwas anders aus.

Grafik (wird später eingefügt)

Erneut schauen wir seitlich auf die Grenz­fläche, bei der sich oberhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₁ befindet, und unterhalb ein elektrisches Feld mit einer Dielektrizitäts­konstante ε_₂. Die Parallel­komponenten der an der Grenz­fläche anliegenden Feld­vektoren haben den gleichen Betrag. Wogegen die senkrecht auf der Grenz­fläche stehenden Komponenten -Normal des elektrischen Feldes unterschied­liche Beträge haben. Auch hier kommt es wieder zu einer Brechung der Feldlinien mit unterschied­lichen Brechungswinkeln.

Für die -Linien bedeutet das:

Das Verhältnis stellt sich dann wie folgt dar:

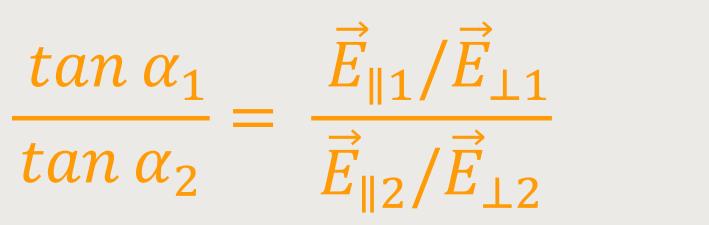
Da aber die Normalkomponenten von stetig sind, fallen diese weg, und es bleibt nur noch stehen:

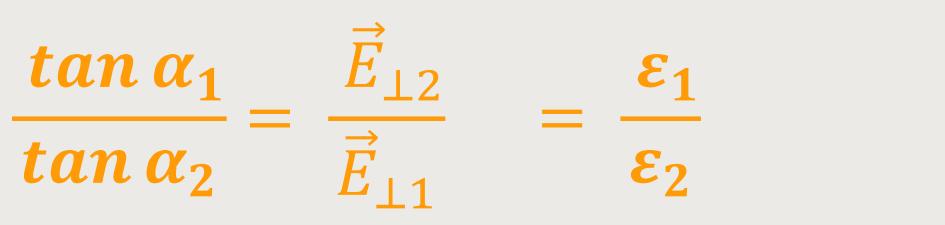
Und damit erhält man ein ähnliches Brechungsgesetz für die -Linien.

Dennoch gibt es einen wesent­lichen Unterschied:

Die -Linien treten immer dann durch das Dielektrikum hindurch, wenn es keine freien Ladungen gibt.
Wogegen die -Linien an den Grenz­flächen entstehen oder enden, weil sich dort die Polarisations­ladungen befinden.

Der -Vektor beschreibt also die Ladungs­verschiebungen. Deshalb spricht man auch von „dielektrischer Verschiebung”.

⇦ Kapitel Kapitel ⇨