• ⇨ Allgemein
• ⇨ Hohlkugel
• ⇨ Unendlich langer geladener leitender Hohlzylinder

Wenn man auf einer geschlossenen Fläche die Rand­bedingungen für die Lösungen der Poisson-Gleichung vorgibt, dann ist die Lösung der Poisson-Gleichung im Innen­raum dieser geschlos­senen Fläche eindeutig bestimmt. Hat man irgendeine Lösung gefunden, die dem genügt, hat man damit auch schon die Lösung erhalten.

Man kann das an einem Beispiel verdeut­lichen. Hierzu betrachten wir eine geladene leitende Hohlkugel. Die Ladung sei Q und der Radius R. Jetzt ist es sinnvoll, die beiden Bereiche, sprich den Außen­raum und den Innen­raum, getrennt zu betrachten.

Die Ladung Q wird sich gleich­mäßig über die ganze Kugel­fläche verteilen. Wenn auch viele gleich­namige Elementar­ladungen vorhanden sind, die sich gegenseitig abstoßen, werden sich diese dennoch gleich­mäßig auf der Außen­seite der Hohlkugel verteilen.

Nun kann man außerhalb eine weitere konzen­trische Kugel­fläche K mit dem Radius r betrachten. Der Radius r wird also größer sein als der Radius R. Wie wird sich nun das elektrische Feld in der Umgebung der Kugel­fläche darstellen? Hierbei lässt sich das Gauß'sche Gesetz anwenden.

Der elektrische Fluss durch die Kugelfläche K ist definiert als:

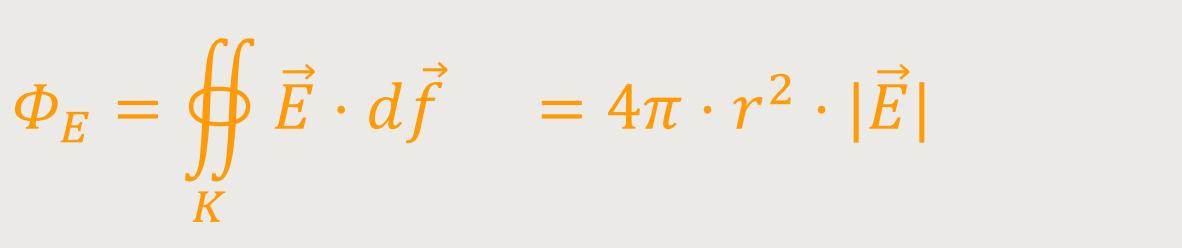
Da aufgrund der Kugel­symmetrie alle Vektoren radial angeordnet sind, liegen diese auch parallel zu den Flächen­vektoren d. Insofern ist der Betrag des elektrischen Feldes überall der gleiche, und man muss nur die Kugel­fläche mit diesem Betrag multiplizieren.

Da andererseits Φ_E = Q /ε_₀ entspricht, kann man jetzt beides gleichsetzen:

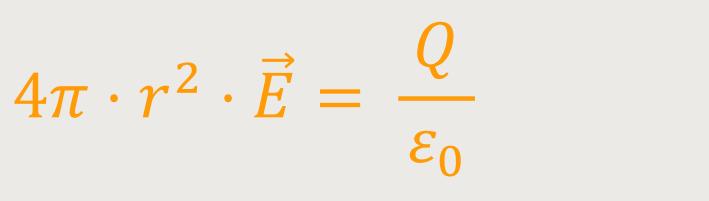
Und damit erhält man sofort den Betrag für die elektrische Feld­stärke (Hohlkugel):

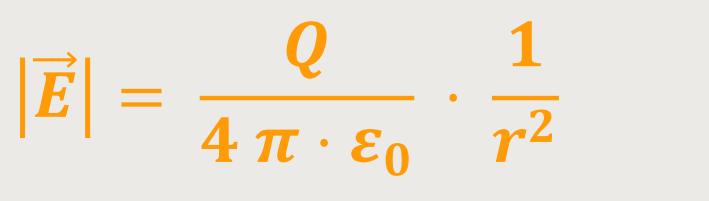
Man erkennt hier sofort, dass die elektrische Feld­stärke im Außen­raum dem einer Punkt­ladung entspricht. Jetzt stellt sich die Frage, wie sieht es nun mit dem Potential aus?

Entsprechend der Definition ergibt sich:

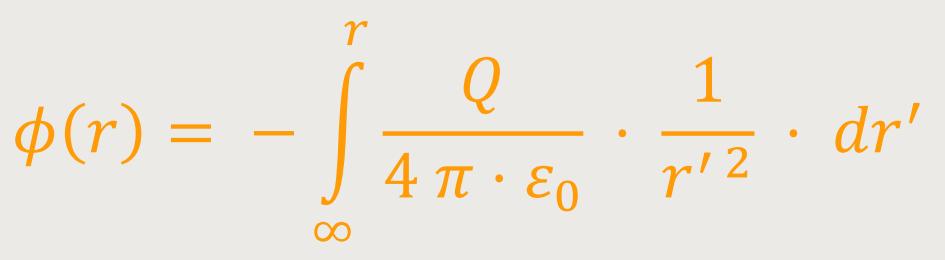
Auch hier liegt der Bezugspunkt wieder im Unendlichen. Nach Integration erhält man:

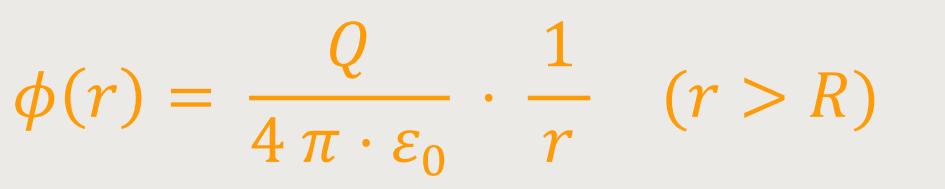
Und damit gilt also für eine geladene Hohlkugel:

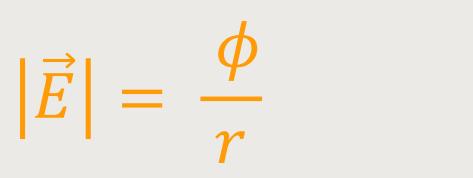
Wenn man eine leitende Ober­fläche betrachtet, bei der das Potential konstant ist, also wenn r = R = const ist, dann entspricht diese Ober­fläche einer Äquipotential­fläche.

Das wäre zum Beispiel dann der Fall, wenn man das Potential an die Erde anschließt:

In diesem Fall nimmt die Feld­stärke || bei abneh­mendem Krümmungs­radius zu. Und das entspricht dem Prinzip des Blitz­ableiters. Wie sieht es dagegen mit dem Innenraum aus?

Jetzt werden wir die Poisson-Gleichung zur Berechnung des Innenfeldes zugrunde legen.

In diesem Fall ist r ≤ R. Der Innen­raum ist somit ladungs­frei. Und damit Δϕ = 0, was gleich­bedeutend ist mit der Laplace-Gleichung. Wie bereits erwähnt ist die geladene Hohlkugel eine Äquipotential­fläche. Auf dieser Hohlkugel ist das ϕ = const. In diesem Fall ist eine Rand­bedingung vorge­geben und dann ist die Lösung, sowohl der Poisson-Gleichung als auch der Laplace-Gleichung, im Innen­raum dieser Fläche eindeutig. Mit anderen Worten, es gibt nur eine Lösung.

Daher ist das Potential im Innenraum konstant, und damit ist der grad ϕ auch Null. Insofern ist der Innenraum feldfrei.

Diagramm (wird später eingefügt)

Hinweis: Die elektrische Feldstärke in der Umgebung einer Punktladung geht betrags­mäßig mit 1 /r² zurück. Während das Potential mit 1 /r zurückgeht.

Die Hohlkugel schirmt den Innenraum gegen äußere Einflüsse ab. Und das ist das Prinzip des „Faraday-Käfigs”.

Alle Koaxialkabel sind quasi solche langen Hohl­zylinder. Denn die Abschir­mungen sind zylindrisch und bewirken, dass im Innen­raum alles abgeschirmt ist.

Beim Zylinder gibt es jedoch eine andere Abhängig­keit des elektrischen Feldes vom Abstand.

Die Ladung des Zylinders nennen wir hier γ und den Radius R. Und wieder betrachten wir die beiden Bereiche, den Außen­raum und den Innenraum.

Grafik (wird später eingefügt)

Die Ladung γ wird sich gleich­mäßig über eine gewisse Länge l des Zylinders verteilen.

Man betrachtet außerhalb eine weitere konzentrische Zylinder­oberfläche Z mit dem Radius r. Der Radius r ist wieder größer als der Radius R. Der elektrische Fluss durch die Zylinder­ober­fläche Z ist definiert als:

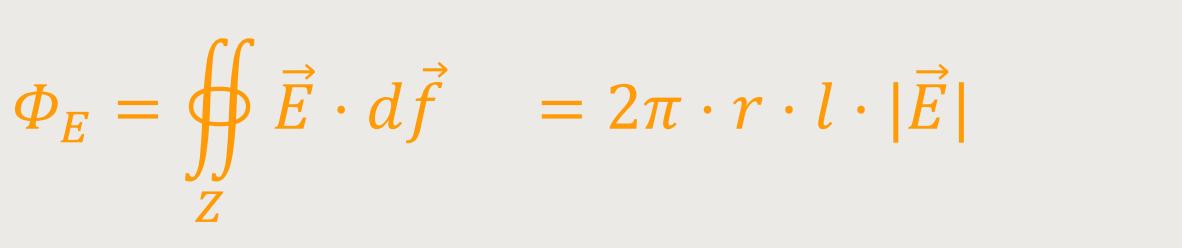
Andererseits gilt nach dem Gauß'chen Gesetz Φ_E = Q /ε₀ = (γ · l) /ε₀ . Nun kann man beides wieder gleichsetzen:

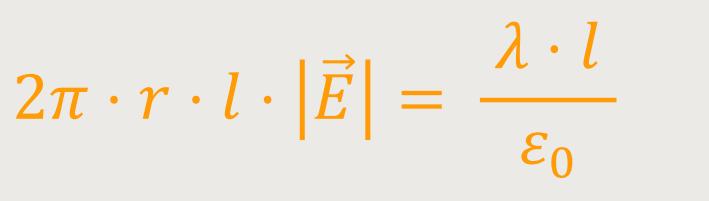
γ ist die Ladung pro Längen­einheit

Und damit erhält man sofort den Betrag für die elektrische Feld­stärke (Zylinder):

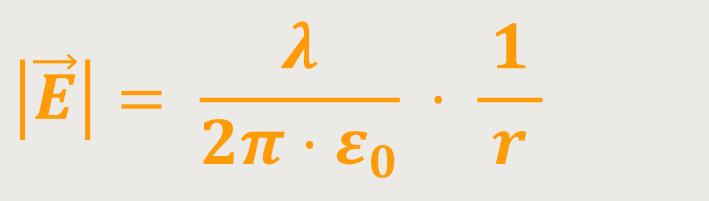
Jetzt stellt sich wieder die Frage, wie sieht es nun mit dem Potential aus?

Entsprechend der Definition ergibt sich:

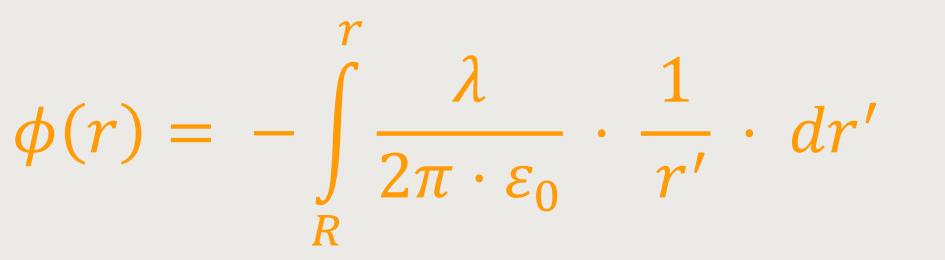
Da 1/ r' · dr' der natürliche Logarithmus (ln) ist, lässt sich auch schreiben:

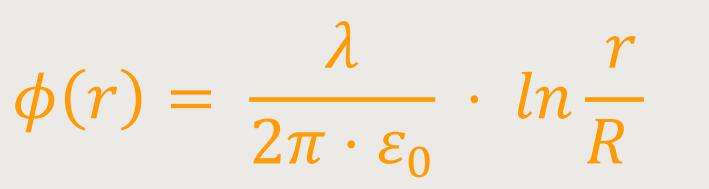
Hier liegt der Bezugspunkt allerdings nicht im Unendlichen, sondern bei r = R.

Abschließend werden wir ebenfalls die Poisson-Gleichung zur Berechnung des Innenfeldes hernehmen.

In diesem Fall ist Q = 0 ⇒ ϱ = 0. Der Innen­raum ist auch hier ladungs­frei. Und damit ist Δϕ = 0, was gleich­bedeutend mit der Laplace-Gleichung ist. Analog zu oben ist der geladene Hohl­zylinder ebenfalls eine Äquipotential­fläche. Auf diesem Hohl­zylinder ist das ϕ = const. Auch hier ist eine Rand­bedingung vorgegeben, und dann ist die Lösung sowohl der Poisson-Gleichung als auch der Laplace-Gleichung im Innen­raum dieser Fläche eindeutig.

Somit ist das Potential im Inne­nraum konstant, und dann ist der grad ϕ auch Null. Und damit ist der Innenraum feldfrei.

Diagramm (wird später eingefügt)

Die Kurvenverläufe schauen sehr ähnlich aus. Nur dass die elektrische Feld­stärke beim Hohl­zylinder nicht mehr betrags­mäßig mit 1 /r² zurück­geht, wie das bei der Hohlkugel der Fall ist.

Wenn man zum Beispiel eine Punkt­lichtquelle wie die Sonne betrachtet, nimmt die Intensität im Abstand mit 1/ r² ab.

Nun gehen wir der Frage auf den Grund, wie Ladungen getrennt werden können.

⇦ Kapitel Kapitel ⇨