Wie lassen sich die Kapazitäten von Kondensatoren berechnen?

In Anlehnung an das vorherige Kapitel behalten wir im Sinn, dass wir nach wir vor elektro­statische Felder betrachten werden. Daher lässt sich die Spannung als Potential­differenz darstellen, sprich als Differenz der Potentiale der beiden Elektroden. Wir möchten kurz einige der geläufigsten Kondensatoren gegenüberstellen.

Bei der Hohlkugel war das äußere Feld so gestaltet, als hätte man eine Punkt­ladung mit gleicher Gesamt­ladung vorliegen. Und innerhalb der Hohl­kugel ist die Feld­stärke gleich Null.

Beim Kugelkondensator betrachtet man „zwei” Kugeln, die konzen­trisch um einen gemeinsamen Punkt angeordnet sind.

Grafik (wird später eingefügt)

Beide Kugeln sind leitend und geladen, wobei die innere eine Ladung +Q trägt, und die äußere eine Ladung −Q. Zusätzlich gibt es im Innenraum ein Potential ϕ_i und im Außen­raum ϕ_a. Die Gesamt­ladung ist gleich Null. Der Außen­raum ist wegen des Gauß'schen-Gesetzes feldfrei. Der Innen­raum der inneren Kugel ist ebenfalls feldfrei. Wenn ein Bereich feldfrei ist, dann wird das Potential dort konstant sein.

Für die Spannung zwischen den beiden Kondensator­platten gilt:

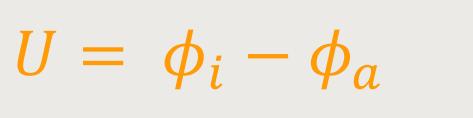
Wenn man die Spannung bei vorge­gebener Ladung kennt, lässt sich damit die Kapazität des Kugel­kondensators ausrechnen.

Zur Berechnung benötigt man zunächst beide Potentiale. Das Potential ϕ_i der inneren Kugel stellt sich in Anlehnung an die Betrachtung der Hohlkugel wie folgt dar:

Des Weiteren gibt es den Bereich in der Mitte zwischen r_i bis r_a:

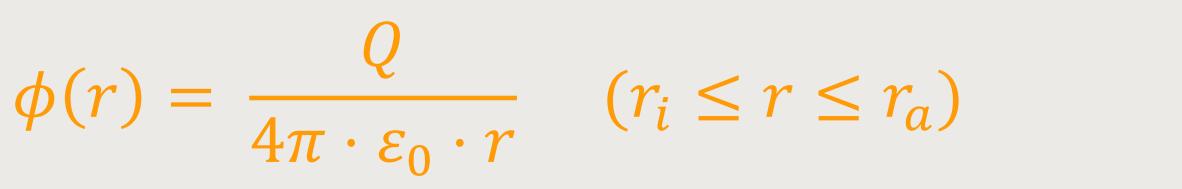
Das Potential wird in diesem Fall gebildet aus dem Außen­raum der inneren Kugel. Da der Innen­raum der äußeren Kugel wegen der inneren Kugel nicht hohl ist, liegt eine Ladung vor. Dennoch trägt die äußere Kugel nichts zu dem Potential bei, weil der eigent­liche Innen­raum der äußeren Kugel in Analogie zu einer Hohl­kugel im klassischen Sinne feldfrei ist.

Nun definieren wir noch das Potential ϕ_a der äußeren Kugel:

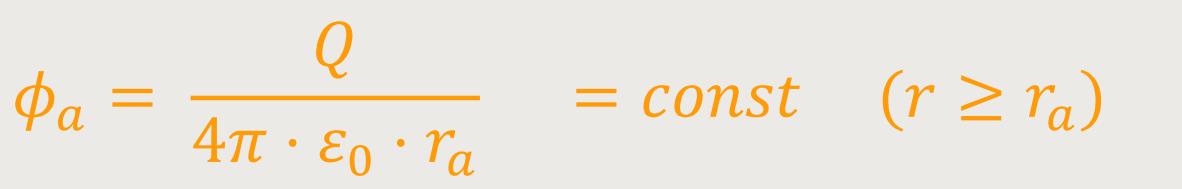
Wir erinnern uns: Das elektrische Feld ist definiert als:

Diagramm (wird später eingefügt)

Jetzt, wo man beide Potentiale kennt, lässt sich die Kapazität ermitteln.

Wie wir bereits betrachtet haben, stellt sich die Kapazität dar als:

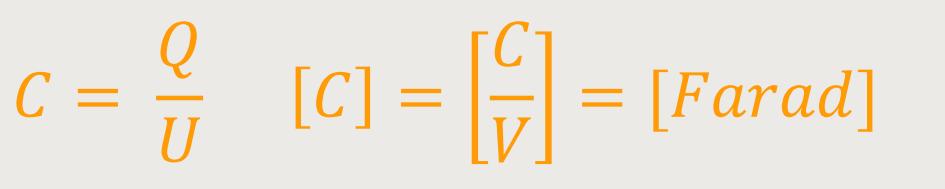
Nach Umstellen und Einsetzen der beiden Potentiale erhält man die Beziehung für die Spannung:

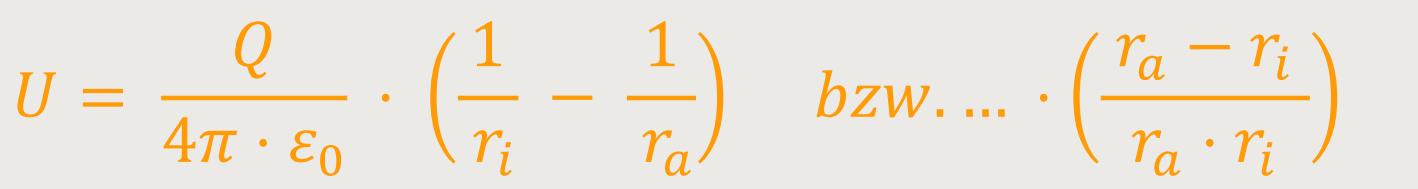
Daraus folgt:

Also, sind die zwei Radien bekannt, lässt sich damit die Kapazität des Kugel­kondensators ausrechnen.

Was passiert aber, wenn die äußere Kugel immer größer wird? Grundsätz­lich ist es so, je kleiner die Differenz der beiden Radien ist, desto größer wird die Kapazität sein. Und wenn man eine gewisse Potential­differenz zwischen der inneren und der äußeren Kugel hat, aber den Abstand kleiner macht, dann wird auch die Potential­differenz bei gleicher Ladung kleiner. Die Schluss­folgerung daraus ist, je größer die Kapazität, desto kleiner wird die Spannung sein.

Und was passiert, wenn die äußere Kugel gegen unendlich geht, zum Beispiel wie bei der Erde?

Der Innenradius r_i entspricht in diesem Fall dem Erdradius R. Dann ergibt sich für die Kapazität der Erde:

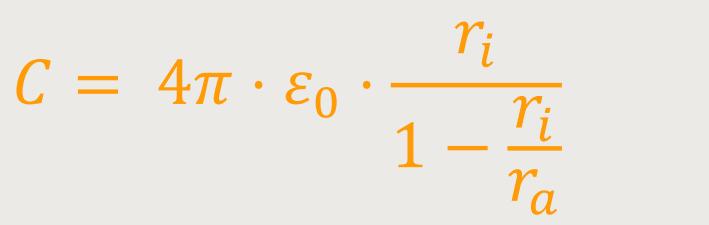
Schließlich bleibt nur mehr übrig:

Bezogen auf die Erdkugel erhält man:

Diagramm (wird später eingefügt)

Analog zur Hohlkugel lassen sich die Potentiale entsprechend herleiten. Und die Kapazität eines Zylinder­kondensators stellt sich dar als:

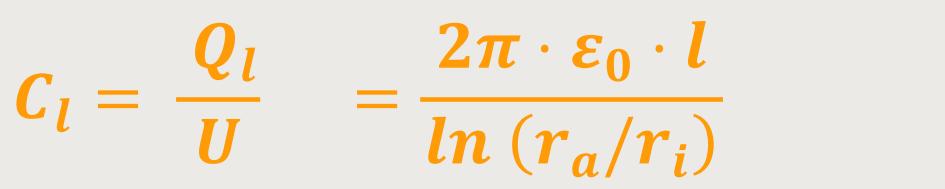
Zylinderkondensatoren mit einer Innen- und Außen­elektrode werden in der Praxis sehr vielseitig verwendet. Diese Gleichung eignet sich auch für die Berechnung der Kapazität einer Koaxial­leitung mit einer definierten Länge l.

Bei der weiteren Betrachtung gilt:

A   ist die Plattenfläche
d   ist der Plattenabstand

Grafik (wird später eingefügt)

Die eine Platte hat ein Potential ϕ₁ mit einer positiven Ladung. Und die andere Platte befindet sich auf dem Potential ϕ₂ mit einer negativen Ladung. Das elektrische Feld liegt zwischen den beiden Platten.

Die elektrischen Feld­vektoren zeigen von der positiven Platte zur negativen Platte. Die Spannung ist wie oben nichts anderes als:

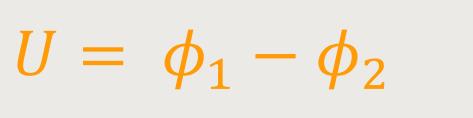
Der Innenraum (Zwischenraum) ist auch hier ladungs­frei. Die Ladungen sitzen nur auf den Platten. Jetzt interessiert uns besonders das Potential ϕ im Innenraum. Deshalb verwendet man hier die Laplace-Gleichung Δϕ = 0. Wenn man nur ein eindimen­sionales Problem betrachtet, bzw. die anderen beiden Komponenten Null sind, reduziert sich die Laplace-Gleichung auf:

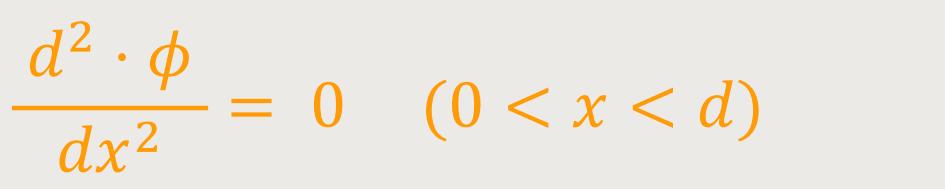
Außerdem gilt als Rand­bedingung:

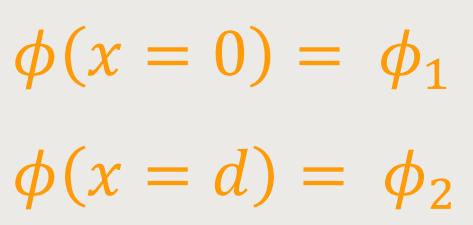
Durch Integration ergibt sich jetzt:

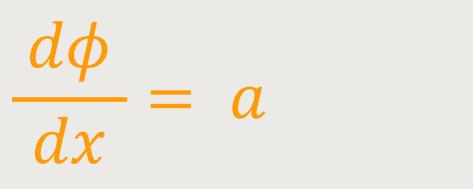
a   ist eine Konstante

Durch nochmalige Integration erhält man:

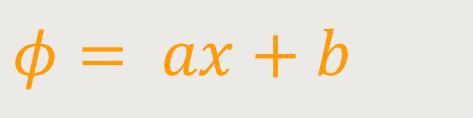
Dadurch kommt es zu einer linearen Abhängig­keit des Potentials von x, wobei a und b Konstanten sind. Aller­dings sind diese Konstanten noch nicht bekannt. Da jedoch zwei Rand­bedingungen vorgegeben wurden, werden die Konstanten nachfolgend so gewählt, dass diese Bedingungen richtig erfüllt sind. Wir betrachten also ein Randwertproblem.

Wenn man die Rand­bedingungen entsprechend berücksichtigt, erhält man:

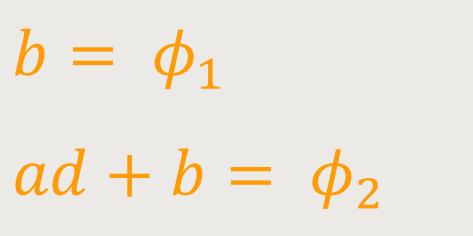
Und damit lässt sich die Differenz dieser Potentiale ermitteln, und somit auch die Spannung ausrechnen.

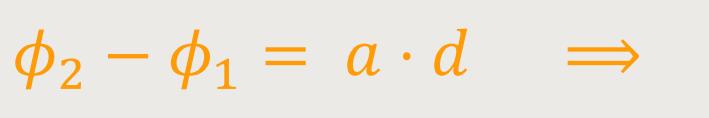
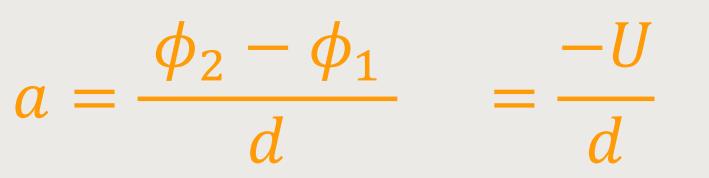
Wenn man das jetzt entsprechend einsetzt ergibt sich:

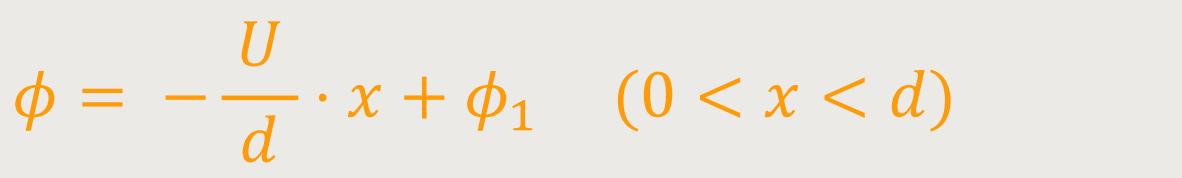
Für die elektrische Feldstärke gilt dann:

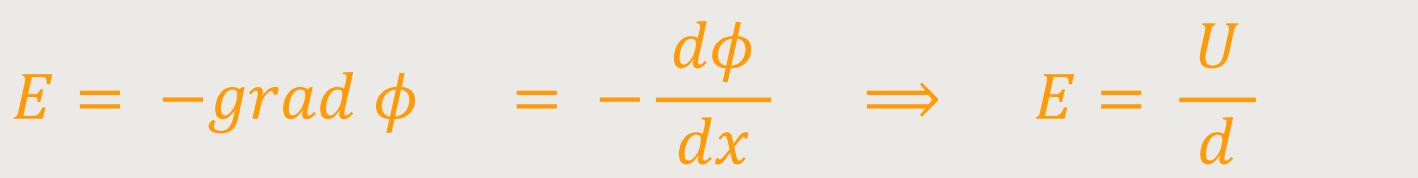
Grafik (wird später eingefügt)

Wie hängt das jetzt mit der Kapazität bzw. der Ladung zusammen?

Zunächst interessiert uns der elektrische Fluss Φ_E im Innenraum des Kondensators:

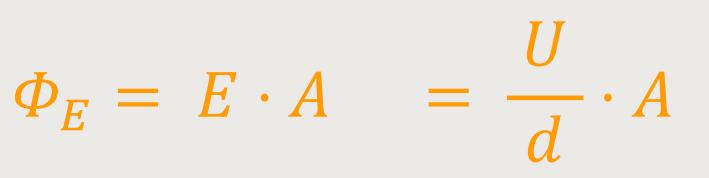
Weil nach außen hin kein elektrischer Fluss austritt, ist Φ_E bereits der Gesamt­fluss aus einer Platte. Unter Verwendung des Gauß'schen-Gesetzes gilt:

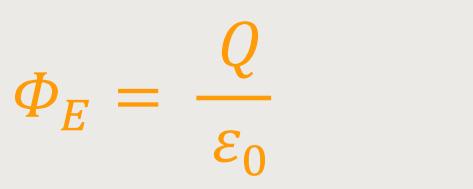
Nun kann man beide Beziehungen miteinander vergleichen:

Wenn man das entsprechend in die Gleichung für die Kapazität einsetzt, ergibt sich für den Platten­kondensator:

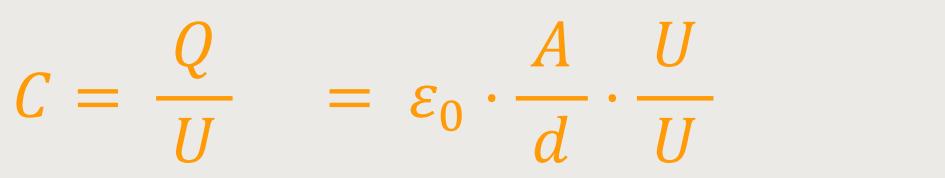
Oder verkürzt ausgedrückt:

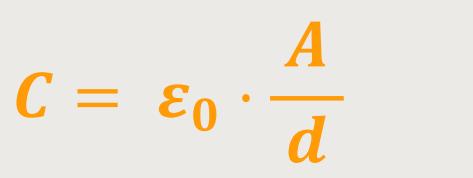
Somit ist die Kapazität proportional zur Platten­fläche. Je größer die Fläche ist, desto mehr Ladung lässt sich auf die Platte bringen. Und je näher die Platten beieinander stehen, desto größer wird die Kapazität.

In einem Versuchsaufbau lässt sich zeigen, dass durch die Änderung des Abstands der Platten sich das elektrische Feld nicht ändert. Auch die Ladungen bleiben gleich. Die Ladungen sind quasi die Quellen des elektrischen Feldes. Das Feld bleibt homogen.

Wenn die Platten dagegen weiter auseinander gehen, wird die Spannung zwischen den Platten bei unverändertem elektrischem Feld größer werden. Denn die Spannung ist definiert als Arbeit pro Ladungs­einheit. Und wenn die Spannung anwächst, wird damit auch die verrichtete Arbeit größer.

⇦ Kapitel Kapitel ⇨