„Dielektrika” sind in der Regel Fest­körper, manchmal auch Flüssig­keiten oder Gase. Es sind im Grunde Medien, da praktisch keine elektrische Leitfähig­keit haben. Das Anwesenheit solcher Dielektrika verändert das vorhandene Feld in einer gewissen Weise. Dabei spielen die jeweiligen molekularen Eigen­schaften des Dielektrikums eine Rolle. Dabei geht es vor allem um die Eigen­schaft, dass Moleküle sogenannte „Dipole” sein können.

Grafik (wird später eingefügt)

Bei so einem „elektrischen Dipol” betrachtet man eine negative und eine positive Ladung, die sich beide in einem gewissen Abstand d zueinander befinden. Dabei schaut man sich den Vektor 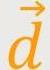an, der von −Q nach +Q gerichtet ist. In der Mitte des Vektors liegt der Ursprung des betrachteten Koordinaten­systems. Anschließend schaut man sich irgendeinen Punkt P im Umfeld der Ladungen an. Dazu beleuchtet man die Orts­vektoren von den jeweiligen feld­erzeugenden Ladungen hin zum Punkt P. Der erste Orts­vektor zeigt vom Ursprung zum Punkt P. Dann gibt es noch einen zweiten Orts­vektor ₁, der von der positiven Ladung zum Punkt P zeigt, und einen dritten Orts­vektor ₂, der von der negativen Ladung zum Punkt P zeigt.

Wenn der Abstand d relativ klein ist gegen­über der Distanz zum Punkt P gelten folgende Beziehungen:

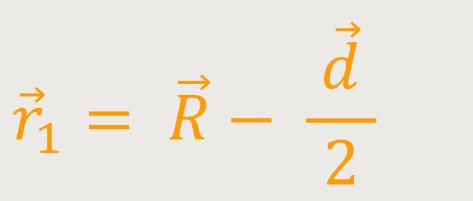
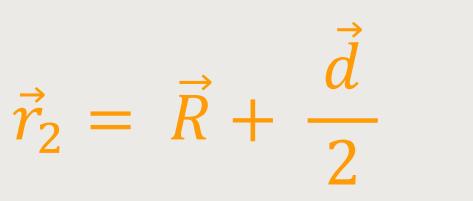
Um sich ein Bild davon zu machen, wie dieses Feld konkret ausschaut, betrachtet man die Über­lagerung der Felder ausgehend von der jeweiligen Ladung. Hierzu spielt die Definition des elektrischen Dipol­moments eine wichtige Rolle:

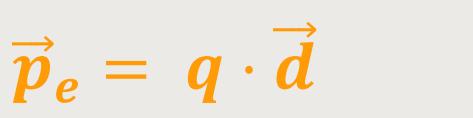
Das elektrische Dipol­moment ist gleich­gerichtet mit dem Vektor 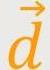, und ist ein Vielfaches dieses Vektors. Und dieses Vielfache entspricht letztlich der Größe der Ladung.

Das Potential am Punkt des Orts­vektors beim Punkt P ist gegeben als:

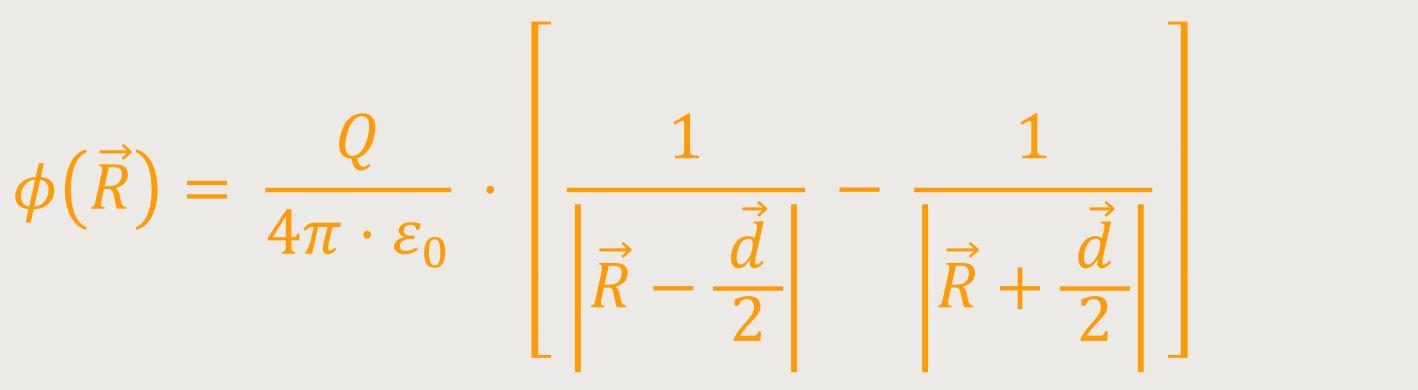
Für den Fall das ||>>||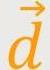, kann man nun eine Reinentwicklung vornehmen:

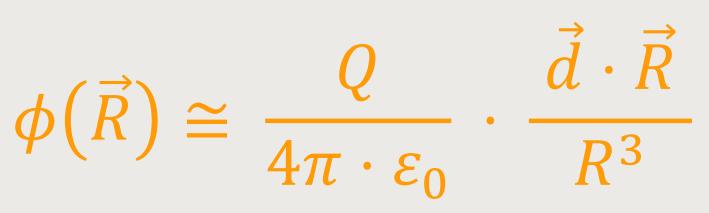
(Hinweis: Der Rechenweg hierzu wurde weggelassen)

Das lässt sich weiter umformen:

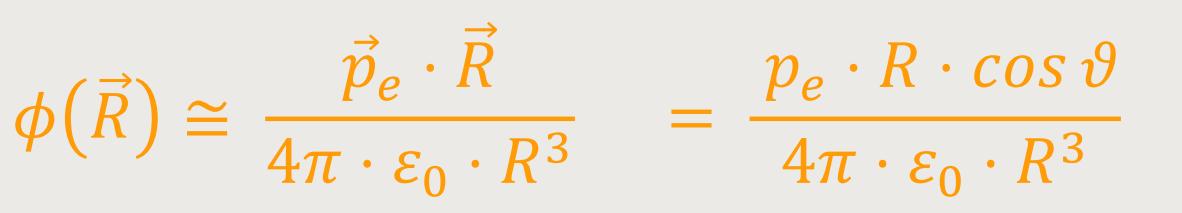
Nach Kürzen folgt daraus:

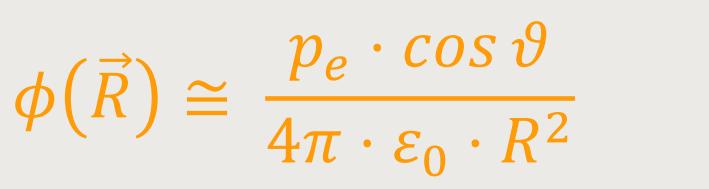
Damit erhält man ein elektrisches Potential, das hierbei mit 1 /R² beschrieben wird. Dieses Potential nimmt demnach stärker ab, als bei der Punktladung.

Für die elektrische Feldstärke gilt dann:

Zusammenfassend lässt sich sagen, dass das Feld in der Umgebung eines elektrischen Dipols stärker abfällt, als das Feld einer Punktladung.

Grafik (wird später eingefügt)

Das Dipolmoment lässt sich relativ leicht ausrechnen:

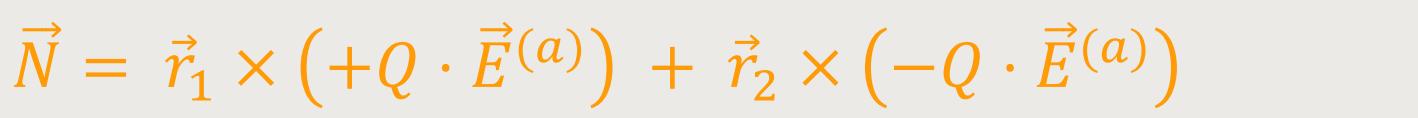
±Q  sind die jeweiligen Ladungen
  sind die Ortvektoren der jeweiligen Ladungen
^(a) ist die äußere Feldstärke

Nach Umformung erhält man:

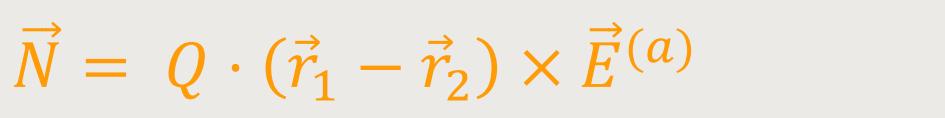
Für das Dipolmoment in einem homogenen elektrischen Feld gilt also:

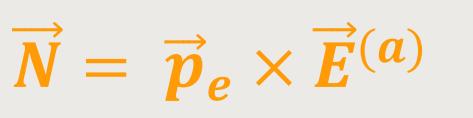
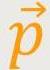_e   ist das elektrische Dipolmoment

Wenn der Vektor des elektrischen Dipol­moments und der Vektor der äußeren Feld­stärke parallel zueinander sind, ist das Kreuz­produkt gleich Null, und dann liegt kein Dipolmoment vor.

Wie wir anschließend noch sehen werden, spielen Dipole auch bei isolierenden Stoffen eine wesentliche Rolle.

Wenn man zwischen die beiden Platten eines Platten­kondensators ein Dielektrikum einbringt, geht je nach Material des Dielektrikums die Spannung unter­schiedlich zurück. Wie lässt sich das interpretieren?

Grundsätzlich wird weiterhin ein gewisser Anteil des elektrischen Feldes durch das Dialektrikum hindurch­dringen. Auch in einem nicht­leitenden Körper gibt es somit elektrische Felder.

Um die Unterschiede zu erkennen, werden wir jetzt verschiedene Anordnungen gegenüber­stellen.

Grafik (wird später eingefügt)

Das elektrische Feld bzw. die elektrische Feld­stärke zwischen den Platten im Vakuum nennen wir _vac .

Wenn man sich um die positiv geladene Platte eine geschlossene Fläche denkt, dann ist laut Gauß'schem-Gesetz der gesamte elektrische Fluss aus der Fläche heraus definiert als:

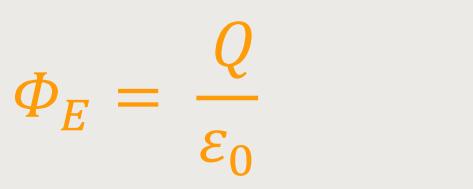
Außerdem ergibt sich laut Definition, dass der elektrische Fluss in diesem Fall Φ_E = A · _vac entspricht.

Wenn man beide Beziehungen gleichsetzt, ergibt sich:

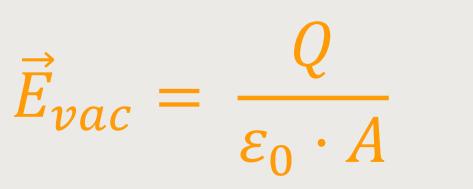
Da aber Q /A die Flächen­ladungsdichte σ (Ladung pro Flächen­einheit) ist, lässt das noch umformen:

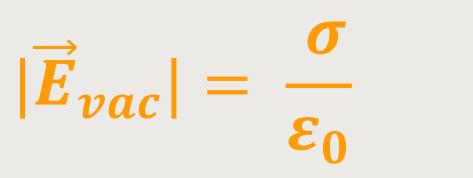
Auch hierbei erkennt man, dass die elektrische Feld­stärke nicht vom Abstand der Platten abhängt.

Grafik (wird später eingefügt)

Grafik (wird später eingefügt)

Ein Dielektrikum besteht grundsätzlich aus Molekülen oder Atomen. Und diese Moleküle werden im Allgemeinen aufgrund ihrer Anordnung ein elektrisches Dipolmoment haben können. Somit werden sich diese, unter dem Einfluss des elektrischen Feldes zwischen den Platten, auch verdrehen können.

Die Moleküle im Dielektrikum werden sich, soweit es ihnen möglich ist, so aus­richten, dass sich die ungleichen Ladungen jeweils anziehen. Die Dipol­momente zeigen dann in die gleiche Richtung wie das elektrische Feld, nämlich von Plus nach Minus.

Man kann sich dieses Dielektrikum in verschiedene Bereiche zerlegt denken. An den Rändern des Dielektrikums gibt es zu den Platten hin Grenz­schichten. Die eine Grenz­schicht zeichnet sich durch einen negativen Bereich aus und die andere Grenz­schicht entsprechend durch eine positive Ladungs­verteilung. Im Innen­raum des Dielektrikums ist alles ausgeglichen. In Summe ist der Innen­raum demnach elektrisch neutral, weil sich die Ladungen alle kompensieren.

Die Grenzschichten nennt man auch Polarisations­schichten, sodass man in den Grenz­schichten einer­seits eine Ladung −Q_pol hat, und ander­seits eine Ladung +Q_pol. Im Grunde bedeutet das, dass sich im Kondensator ein zweiter Kondensator befindet, bei dem die Grenz­schichten ihrerseits wieder wie zwei Platten fungieren. Allerdings ist jetzt der innere Kondensator durch die Ladungs­anordnung entgegen­gesetzt. Natürlich wird er nicht die gleichen Ladungen tragen, weil es ja kein leitendes Medium ist. Auf diese Weise entsteht ein Gegen­feld, das sich mit dem ursprüng­lichen Feld über­lagert. Und dadurch wird sich letztlich eine verringerte Feldstärke ergeben.

Im Innern stellt sich diese elektrische Feldstärke dann als _diel dar. Die Feld­stärke im Dielektrikum wird im Allgemeinen kleiner ausfallen als im Vakuum.

Grafik (wird später eingefügt)

Wie schaut jetzt die Polarisation des Dielektrikums pro Volumeneinheit aus?

Das ist einfach die Summe aller Dipolmomente pro Volumeneinheit:

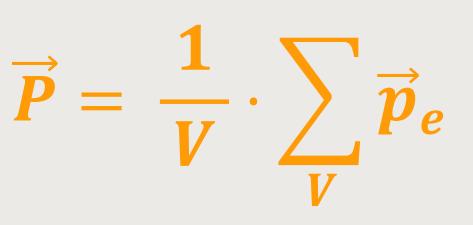
V   ist das Volumen des Dielektrikums

Wenn man ein einheitliches Material für das Dielektrikum betrachtet, dann werden die elektrischen Dipolmomente 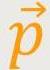_e betrag­smäßig alle gleich sein. Und wenn diese im Idealfall alle gleich­artig und parallel ausgerichtet sind, lässt sich die Beziehung noch einfacher ausdrücken:

N   ist die Anzahl aller Moleküle im Dielektrikum (pro Volumeneinheit)

Aber letztlich ist es das Ziel, das elektrische Feld zu berechnen. Dabei spielt die Flächen-Ladungs­dichte in den Grenz­schichten eine wesent­liche Rolle. Bei der Größen­ordnung der Grenz­schichten betrachtet man nur eine Molekül­dicke. Die Schicht­dicke wird hierbei etwa d entsprechen, also dem Abstand zwischen der positiven und der negativen Ladung.

Für die Polarisationsladung in der Grenzschicht erhält man:

A · d   ist das Volumen der Grenzschicht

Die Polarisationsflächenladungsdichte ist somit definiert als:

Und damit lässt sich jetzt auch das elektrische Feld im Inneren des Dielektrikums ermitteln. Die Polarisations­feld­stärke entspricht ja der Flächen­ladungs­dichte dividiert durch ε_₀.

Es ergibt sich für die Polarisationsfeldstärke (analog zum Vakuumkondensator):

Aufgrund dessen ließe sich das Ganze auch als Vektor­gleichung darstellen.

Grafik (wird später eingefügt)

Die Vektoren der Polarisations­feld­stärke _pol sind entgegen­gerichtet der Dipolmomente pro Volumen­einheit. Dadurch kommt es zu einer Abschwächung des Feldes, weil es an der Struktur der Dipole liegt. Denn die elektrischen Dipole können als Anordnung zweier entgegen­gesetzter Ladungen aufgefasst werden.

Hinweis: Bei den magnetischen Phänomenen und bei der Beeinflussung von Magnet­feldern durch Magnetika, insbesondere durch Feromagnetika, gibt es einen entscheidenden Unterschied. Bei den Magnet­feldern ist die Polarisations­flussdichte gleich­gerichtet mit dem Polarisations­vektor. Dort kommt es zu einer Verstärkung des magnetischen Feldes.

Grafik (wird später eingefügt)

Wir konnten also erkennen, dass der durch +Q_pol und −Q_pol gegebene innere Konden­sator eine Feld erzeugt, welches dem durch +Q und −Q erzeugten äußeren Feld entgegen­gerichtet ist.

Möchte man jetzt entsprechend zu einer Vektor­gleichung über­gehen, muss man aufgrund der Anordnung der Vektoren ein Minus hinzufügen:

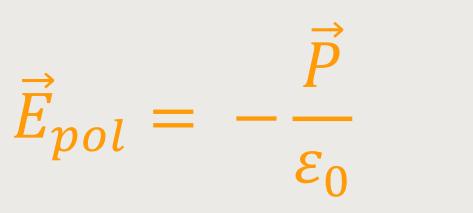
Und damit ergibt sich für die elektrische Feldstärke im Dielektrikum:

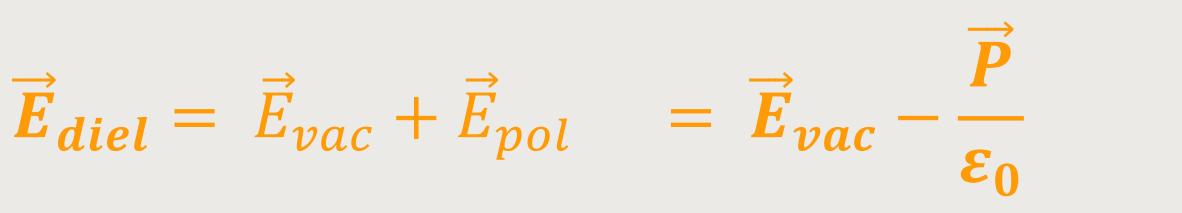
Aber um das konkret zu berechnen, benötigen wir natürlich noch den Polarisations­vektor . Auf den werden wir jetzt kurz Bezug nehmen.

So ein Dielektrikum kann auf zweierlei Weise polarisiert werden. Einerseits in Form einer Orientierungs­polarisation. Quasi so wie oben behandelt, indem sich vorhandene Dipole orientieren und entsprechend ausrichten. Dadurch kommt es zu permanenten Dipolen.

In vielen Fällen aber tritt eine Verschiebungs­polarisation auf. In einem solchen Fall ist ein Molekül von einer Elektronen­hülle umgeben. Und wenn man ein solches Molekül in ein äußeres elektrisches Feld bringt, wird sich der positive Atomkern auf die eine Seite verschieben wollen, und die Elektronen­hülle auf die andere Seite. Dadurch wird letztlich ein Dipol induziert.

Das dadurch entstehende Dipolmoment lässt sich definieren als:

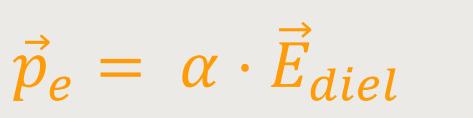
α   ist die Polarisier­barkeit als Proportionalitäts­faktor

Χ_e   ist die dielektrische Suszeptibilität des Dielektrikums

Diese „Suszeptibilität” ist eine Material­eigenschaft, welche die Fähigkeit zur elektrischen Polarisierung in einem eingeprägten elektrischen Feld angibt. Der Wert kann von einer Vielzahl von Parametern abhängen. Dazu zählen die Frequenz und Ausrichtung des betrachteten elektrischen Feldes oder eine Polarisation des Materials durch elektrische Ströme.

Daraus ergibt sich jetzt für die elektrische Feldstärke im Dielektrikum:

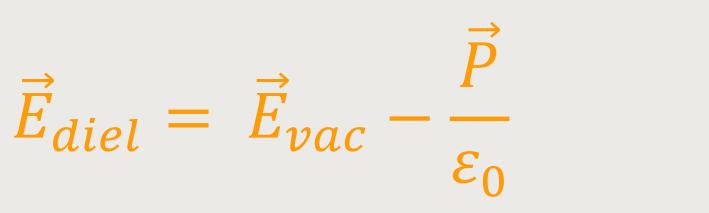
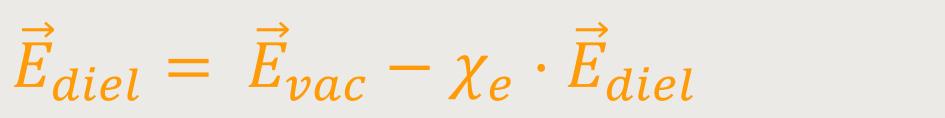
Daraus folgt wiederum:

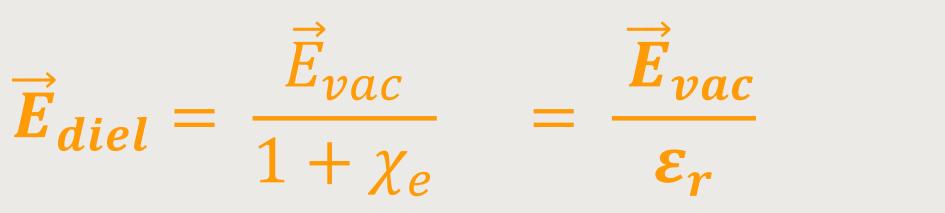
ε_r   ist die relative Dielektrizitätskonstante

Diese „relative Dielektrizitäts­konstante” ist der Faktor, um den das Feld im Dielektrikum kleiner ist, als die Feld­stärke im Vakuum. Mit anderen Worten, die elektrische Feld­stärke im Dielektrikum ist um den Faktor 1 /ε_r kleiner, als die elektrische Feldstärke im Vakuum.

Was bedeutet das aber für die freien, ungebundenen Ladungen im Dielektrikum? Auf diese Frage gehen wir im nächsten Kapitel ein.

⇦ Kapitel Kapitel ⇨