Bei der Betrachtung des Platten­kondensators gehen wir jetzt einen Schritt weiter. Zwischen den Kondensator­platten herrscht jetzt eine gewisse Kraft. Da die eine Platte positiv geladen ist und die andere negativ, ziehen sich beide Ladungen gegenseitig an.

Wenn man einen Kondensator schrittweise auflädt, wird das elektrische Feld zwischen den Platten immer stärker. Demnach muss immer mehr Arbeit verrichtet werden, weil die Kraft­wirkung auf jeden weiteren Ladungs­zuwachs Δq immer größer wird. Um also den ungeladenen Kondensator auf eine gewisse Ladung Q aufzuladen, muss Arbeit investiert werden.

Die Arbeit und die Spannung stehen dabei in einem engen Zusammen­hang. Die Arbeit ist dann die Spannung zwischen den Platten multi­pliziert mit der Ladung Δq. Am Anfang ist die Spannung zwar Null, aber sie nimmt bei jedem Ladungs­vorgang weiter zu. Und damit steigt auch die Arbeit.

Diese elektrische Arbeit lässt sich als Integral darstellen:

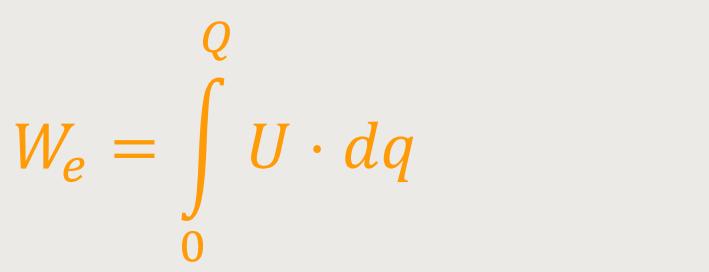
Wenn man berücksichtigt, dass U = q /C ist, dann ist dieses q die jeweils momentane Ladung des Kondensators während des Ladungs­vorgangs. Da die Kapazität eine Konstante ist, kann man sie vor das Integral schreiben, als:

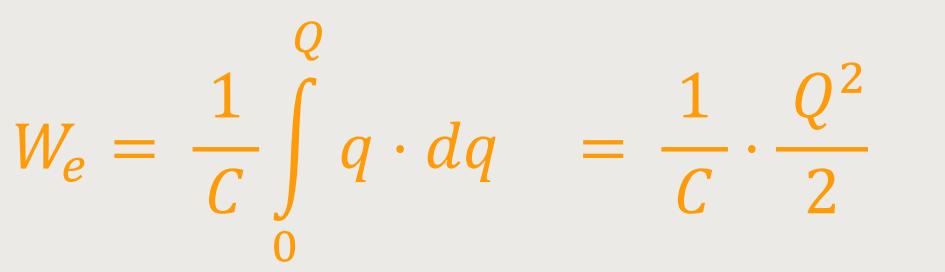
Also, diese Arbeit muss man investieren, um den Kondensator mit einer Kapazität C von anfäng­licher Ladung Null auf die Ladung Q aufzuladen.

Das lässt sich noch weiter umformen, wobei man hier die Ladung ersetzt:

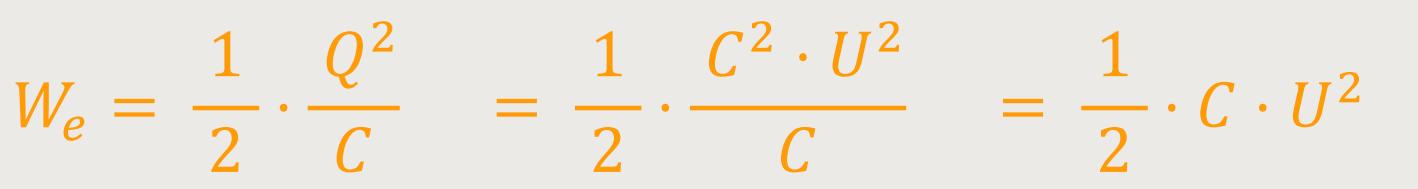
Eine alternative Umformung wäre:

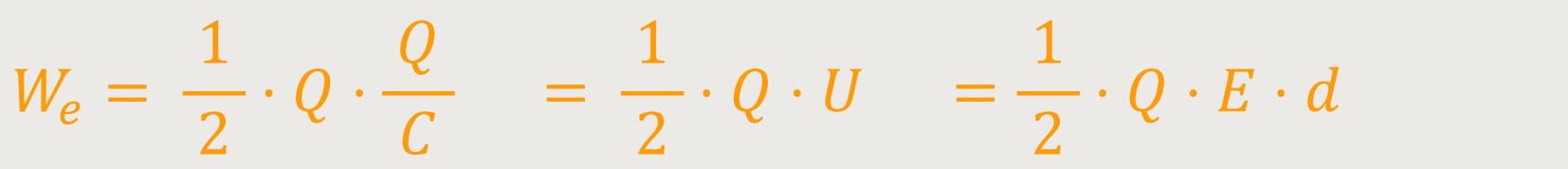
Der Vorteil der zweiten Beziehung liegt darin, dass sich die Kraft besser ausrechnen lässt. Denn hier wird der Abstand der Platten mit berücksichtigt.

Was ist, wenn man den Abstand um ein Δd verändert? Auf jeden Fall wird sich auch die Arbeit entsprechend ändern:

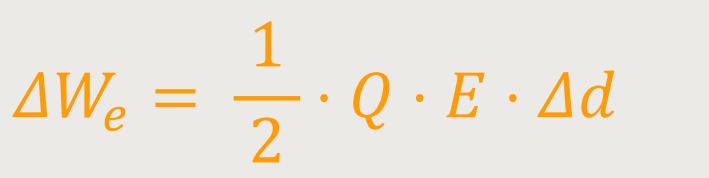
Aus der Definition der Arbeit lässt sich ableiten, dass 1/2 · Q · E der Kraft || zwischen den Platten entspricht.

Dann wäre die Kraft:

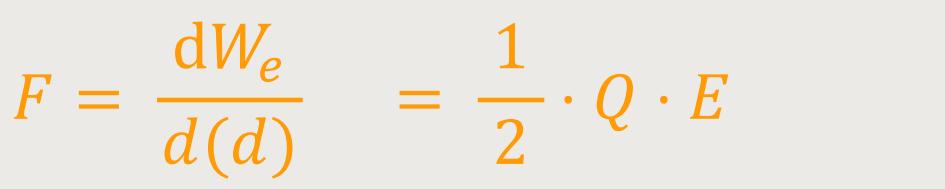
Wie kommt es aber zu dem Faktor 1/2?

Man hat bei dem Kondensator die Situation, dass sich auf beiden Platten unter­schiedliche Ladungen befinden. Jede Ladung für sich trägt zu dem elektrischen Feld zwischen den Platten bei. In diesem Fall trägt jede Platte jeweils zur Hälfte zum gesamten Feld bei. Und dadurch, dass sich Ladungen in Summe kompensieren, ist der Außen­raum feldfrei. Die Kraft kommt dadurch zustande, dass sich eine der beiden Platten im elektrischen Feld der anderen befindet. Aufgrund dessen erfahren beide eine Kraft­wirkung der jeweils anderen Platte. Aber der Kraft­anteil, der von der Platte selbst strammt, bewirkt natürlich keine Kraft auf sich selbst.

Was heißt das konkret für die Kraft?

Wir erinnern uns:

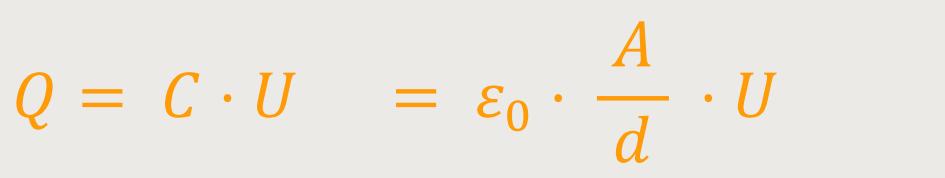
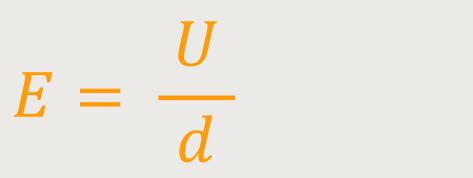
Mit diesen beiden Beziehungen ergibt sich für einen geladenen Platten­kondensator die Kraft:

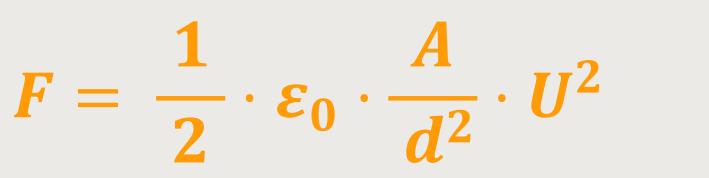
Dieser Formalismus gibt einem sogar die Möglich­keit, rein mechanisch die universelle Konstante ε_₀ ermitteln:

Was uns natürlich noch mehr interessiert, ist der Energie­gehalt. Hierfür rechnen wir uns noch einmal die Arbeit aus (s.o.):

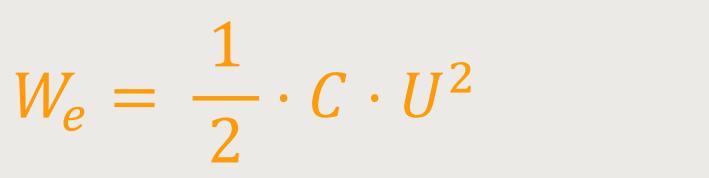
Diese Arbeit hat man in den Kondensator hinein­gesteckt, und somit entspricht das jetzt der Energie, die in dem Kondensator enthalten ist. Auch hier gilt wieder:

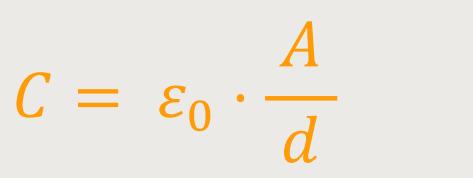
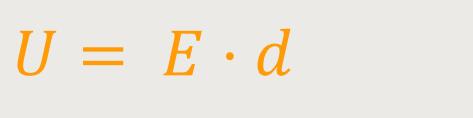
Wenn man diese beiden Beziehungen entsprechend einsetzt, erhält man:

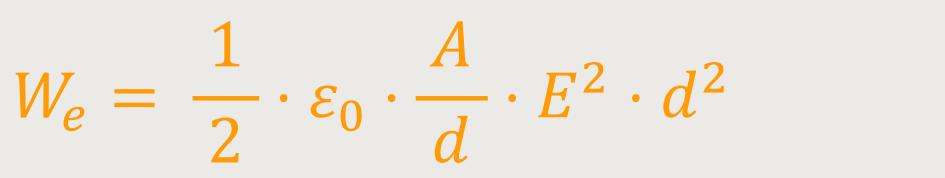
Durch Umformung ergibt sich:

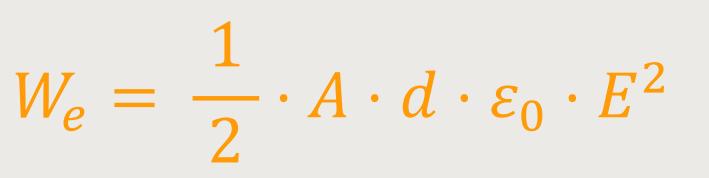
A · d   ist das Volumen des Feldes zwischen den Platten

Dadurch wird deutlich, dass man die Energie nicht den einzelnen Platten zuordnet, sondern dem Feld. Und damit ist das elektrische Feld Träger der Energie. Insofern kann man sich bei der Energie auf die Volumen­einheit beziehen.

Die Energiedichte w beträgt daher:

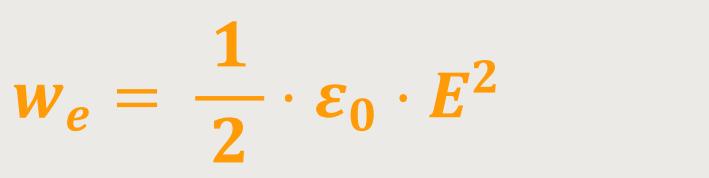
Wie wir später noch sehen werden, hat auch das magnetische Feld eine „Energie­dichte”. Diese Dichte bezeichnet man dann als w_m. Und das gesamte elektro­magnetische Feld ist dann die Summe der beiden Energie­dichten. Denn es gibt ja auch die Ausbreitung elektro­magnetischer Wellen. Und wenn sich solche Wellen­felder ausbreiten, nehmen diese auch ihre Energie mit.

Grafik (wird später eingefügt)

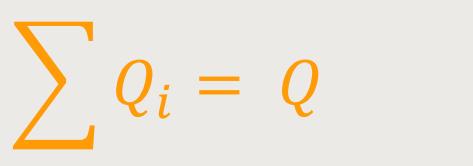
Q_i = C_i · U_i   ist die Einzelladung

Q = C · U₀   ist die Gesamtladung

Wenn man entsprechend einsetzt, ergibt sich:

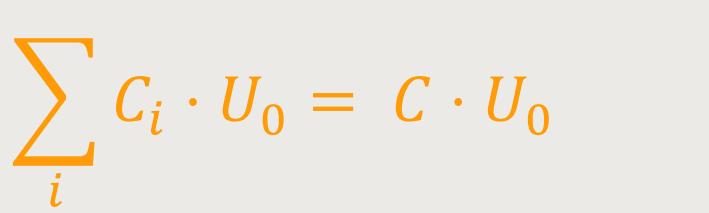
Daraus folgt für die Kapazität:

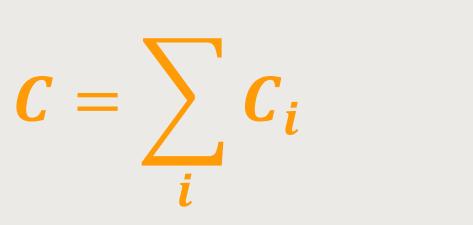
Bei Parallelschaltung von Kondensatoren addieren sich die Kapazitäten zu deren Gesamt­kapazität.

Grafik (wird später eingefügt)

Im nächsten Fall wird es so sein, dass an allen Kondensatoren einzelne Spannungen anfallen. Während bei der Parallel­schaltung an allen Kondensatoren die „Spannung” gleich war, befindet sich jetzt bei der Serien­schaltung im Gegensatz dazu auf allen Kondensatoren die gleiche „Ladung”. Das heißt für die Spannung:

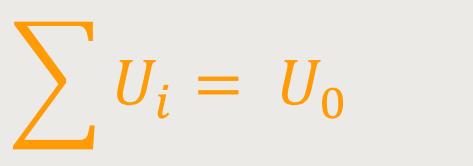
U_i = Q /C_i   ist die Einzelspannung

U₀ = Q /C   ist die Gesamtspannung

Wenn man auch hier entsprechend einsetzt, ergibt sich:

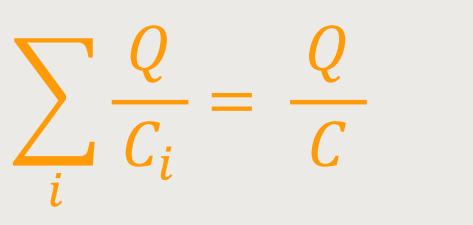
Daraus folgt für die Kapazität:

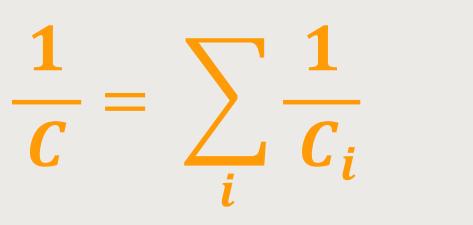
Bei Serienschaltung von Kondensatoren addieren sich die Reziprok Werte der einzelnen Kapazitäten zu deren Gesamt­kapazität.

Nun wollen wir die Material­eigenschaften von Dielektrika in dem elektrischen Feld betrachten. Das Feld muss nämlich nicht zwangs­läufig nur aus Vakuum bestehen. Was passiert beispiels­weise, wenn in einem elektrischen Feld, sprich zwischen die Platten eines Kondensators, ein Medium zwischen geschaltet wird? Formal kann sich dadurch die Kapazität eines Kondensators vergrößern.

⇦ Kapitel Kapitel ⇨