Bei elektrischen Ladungen kommt es bedingt durch deren Ladungs­zustand, hervor­gerufen durch die Einwirkung eines elektrischen Feldes, oft zu Ladungs­verschiebungen. Man spricht dann von „Influenz”.

Bei einem Leiter werden die beweg­lichen Ladungen, dabei handelt es sich fast immer um Elektronen, auf der Ober­fläche verschoben und ändern ihren Platz. Das führt zu ortsab­hängigen Ladungs­dichten. Die fest­sitzenden Atome werden davon nicht beein­flusst. Die Verschiebung erfolgt meist so lange, bis auf die frei­beweglichen Ladungs­träger keine Kraft mehr einwirkt. Mit anderen Worten, das geschieht so lange, bis das ursprüng­liche elektrische Feld durch das elektrische Feld der verschobenen Ladungen vollständig kompensiert wurde und der Innen­raum feldfrei ist. In und auf einem Nicht­leiter können keine Ladungen verschoben werden, es werden aber die vorhandenen Atome bzw. Moleküle polarisiert. Doch dazu später mehr.

Wie wir gesehen haben, stoßen sich Gleich­namige elektrische Ladungen gegen­seitig ab, wogegen sich ungleich­namige anziehen. Bringt man einen Körper mit leitfähiger Ober­fläche in ein elektrisches Feld, so verändert sich auf ihm die Ladungs­dichte. Dies geschieht, weil negative und positive Ladungen durch die Wirkung dieses elektrischen Feldes in andere Richtungen streben. Auf gewissen Flächen gibt es dann mehr Ladungs­träger als auf anderen. Es kommt zu einer unter­schiedlichen Ladungs­dichte. Aber die Gesamt­ladung des Körpers bleibt konstant.

Die Poisson-Gleichung hat die wichtige mathematische Eigenschaft, dass man bei den Lösungen die Rand­bedingungen längs einer geschlos­senen Fläche vorgibt. Damit ist die Lösung der Gleichung für den Innen­raum einer geschlos­senen Fläche eindeutig. Vor allem, wenn die Ober­fläche des Körpers leitend ist und sich zudem die elektrische Ladung im Gleich­gewicht befindet, während der Innen­raum ladungs­frei ist. In einem solchen Fall bezeichnet man die Ober­fläche als Äquipotential­fläche. Und wenn man ein konstantes Potential voraus­setzt, wird die Laplace-Gleichung Δϕ = 0 gleich­falls erfüllt sein. Das bedeutet wiederum, dass die mathema­tische Lösung für den Innen­raum ein konstantes Potential ergibt. Dieser Umstand gilt für jede beliebige geschlossene Fläche!

Wenn man zum Beispiel eine geschlossene leitende Ober­fläche betrachtet, deren Ladung sich im Gleich­gewicht befindet, dann wird längs der ganzen Ober­fläche eines Hohl­körpers das Potential konstant sein. Wäre das nicht der Fall, gäbe es elektrische Felder und dann würde es zu Ladungs­verschiebungen kommen. Und zwar solange bis sich die Ladungen wieder im Gleichgewicht befinden.

Nun könnte man einen Hohl­körper einem äußeren elektrischen Feld aussetzen, indem geladene Körper in dessen Nähe gebracht werden. Oder man bringt diesen Körper in ein Feld zwischen den Platten eines Konden­sators. In einem solchen Fall würden die äußeren elektrischen Felder den Hohl­körper durchsetzen. Wobei der Innenraum feldfrei bleibt. Warum ist das so?

Die beweglichen Ladungen in dem leitenden Hohl­körper beginnen sich durch die Einwirkung des äußeren Feldes so zu verschieben und entsprechend anzuordnen, dass sie selbst ein Feld erzeugen, welches im Innenraum das äußere Feld nahezu kompensiert. Dadurch kommt es, wie bereits erwähnt, zu Ladungs­verschiebungen oder Influenz.

Wenn man bei einem Versuchs­aufbau ausreichend gleich­namige Ladungen „gelöffelt” hat, wird es immer schwieriger weitere Ladungen zu über­tragen. Denn die Ladungen beginnen sich jenseits eines bestimmten Punktes gegen­seitig abzustoßen. Insofern führt das „Becher-Elektrometer” zu einer wesentlich effizien­teren Ladungs­übertragung gegenüber einem flachen Elektrometer. Hinzu sei noch erwähnt, dass die Ladungs­übertragung immer in das „Innere” des Bechers erfolgen muss.

Positive und negative Ladungen wandern zu den entsprechenden Polen, sprich die Ladungs­träger beginnen sich zu verschieben. Ähnliches kann man bei einem Kondensator beobachten.

Die eine Platte (2) ist geerdet. An die andere Platte (1) wird eine Hoch­spannung angelegt. Die Platte (1) wird sich positiv aufladen. Die Platte (2) wird sich entsprechend durch Influenz negativ aufladen, weil von der Erde Ladungs­träger zur geerdeten Platte wandern. Im Innenraum wird sich ein weitgehend homogenes elektrisches Feld ausbilden.

Grafik (wird später eingefügt)

Wenn man nun zwei leitende Körper in den Innenraum des Kondensators einführt, ohne die Kondensator­platten zu berühren, werden sich an beiden Körpern entsprechend negative Ladungen in Richtung der positiven Kondensator­platte ansammeln und negative Ladungen in Richtung der negativen Kondensator­platte. Im Innern der beiden Körper herrscht wieder Feldfreiheit.

Demzufolge ist gleich viel negativer Ladungs­überschuss auf der einen Seite, und gleich viel positiver Ladungs­überschuss auf der anderen Seite.

Grafik (wird später eingefügt)

Kondensatoren sind eine wichtige Anwendung in der Elektro­statik. Bei Kondensatoren geht es darum, Instrumente herzustellen, die in einem gewissen Raum­bereich erhebliche Ladungen speichern können, ohne dass dabei nennens­werte elektrische Felder in deren Umgebung entstehen. Es gibt verschiedene Ausführungen von Kondensatoren. Aber in jedem Fall ist es so, dass zwei entgegen­gesetzt geladene Leiter­flächen angeordnet sind, sprich zwei Elektroden.

Eine dieser Elektroden hat +Q, die andere −Q. Die konkrete Anordnung der Elektroden kann sehr unter­schiedlich sein. Die einfachste Gestaltung ist der Platten­kondensator. Er hat den Vorteil, dass zwischen den beiden Platten ein homogenes elektrisches Feld entsteht. Bei technischen Anwendungen hat man dagegen oft Zylinder­kondensatoren. Aber wie bringt man die Ladung auf die Elektroden?

Grafik (wird später eingefügt)

Zunächst ist der Kondensator ungeladen. Dann wird an einer der beiden Platten eine Spannung angelegt, wobei die zweite Platte geerdet ist. Durch die Spannung kommt die Platte auf ein erhöhtes Potential. Insofern wird sich eine positive Ladung ansammeln. Nach beiden Richtungen wird sich ein elektrisches Feld ausbilden. Bei der zweiten Platte wird es dann so sein, dass diese im Innen­raum kein Feld zulassen möchte, und sich an dieser Platte deshalb negative Ladungen ansammeln. Außen bleiben die positiven Ladungen erhalten. Doch in Summe bleibt die zweite Platte ungeladen, was wieder einer Influenz­erscheinung gleicht. Die geerdete Platte hat also die negative Ladung vom Erdpotential hochgehoben.

Die positive Platte hat nach beiden Seiten hin ein elektrisches Feld, bei dem die Feld­linien von der Platte weg zeigen. Aber bei der negativen Platte zeigen die Feld­linien von beiden Seiten zur Platte hin. Das heißt, außerhalb des Kondensators kompensieren sich die Feld­linien gegenseitig weg. Im Innen­raum dagegen verstärken sie sich. Und damit ist eine Situation erreicht, wo positive und negative Ladungen getrennt gespeichert werden können. Da außer­halb des Kondensators kein elektrisches Feld entsteht, sitzen die Ladungen nur auf den inneren Flächen des Kondensators.

Auf diese Weise lassen sich sehr hohe Ladungen in einem Kondensator speichern. Es zeigt sich, dass die Ladung auf dem Kondensator proportional ist zur gesamten elektrischen Feld­stärke und proportional zur Spannung: Q ∝ || ∝ U₀. Das bedeutet, dass es eine Beziehung geben muss, nämlich dass die Ladung über einen Proportionalitäts­faktor mit der Spannung verbunden ist:

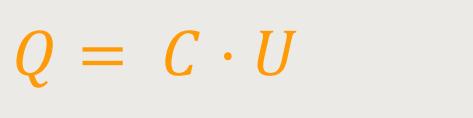
Daraus folgt eine fundamentale Beziehung:

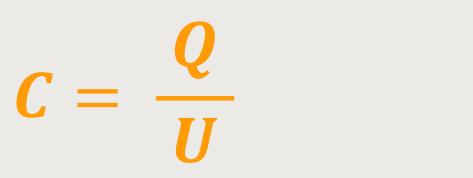
C   ist die Kapazität des Kondensators

Auf den Elektroden befindet sich eine Äquipotential­fläche, denn nur so ist sicher­gestellt, dass das System statisch ist. Die Spannung ist eine wohl­definierte Größe zwischen den beiden Elektronen. Wenn daher ein Kondensator eine hohe Kapazität hat, kann er entsprechend viele Ladungen speichern, wobei gleich­zeitig die Spannung zwischen den Elektroden klein ist.

⇦ Kapitel Kapitel ⇨