Bei unserer Betrach­tung geht es nicht nur um Dehnungen. Was auch berück­sichtigt werden muss ist, wenn man bei einem festen Körper eine „allseitige Kompression” durch­führt. Dann ergibt sich inner­halb des Propor­tionalitäts­bereiches eine völlig analoge Formel zum Hookeschen Gesetz.

Bei der Kompres­sion wird nur das Volumen verringert, aber die Gestalt bleibt gleich. Statt der relativen Längen­änderung ergibt sich jetzt die relative Volumen­änderung:

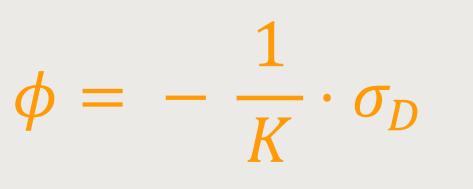
K   ist das Kompressions­modul des jeweiligen Werk­stoffes
σ_d   ist die Druck­spannung

Zur Erinnerung, die Druck­spannung ist die Kraft pro Quer­schnitts­flächen­einheit, die senk­recht auf die Flächen wirkt. In der Formel kommt ein Minus vor, denn wenn der Druck größer wird, wird das Volumen kleiner. Insofern wird das ΔV negativ.

Neben dieser von allen Seiten wirkenden Kompres­sion gibt es auch eine andere grund­sätzliche Art der Verformung, nämlich die bereits kurz erwähnte Scherung. Auch bei Scherungen haben wir keine Volumen­änderung, wohl aber eine Form­änderung. Und der Scherungs­winkel ist der Winkel, um den der Körper schräg verzerrt wird.

Tangential­spannung = Tangentialkraft pro Flächeneinheit

Im Rahmen des Propor­tionalitäts­bereiches gibt es eine ganz einfache Beziehung. Dieser Scher­winkel γ ist propor­tional zur Tangential­spannung τ:

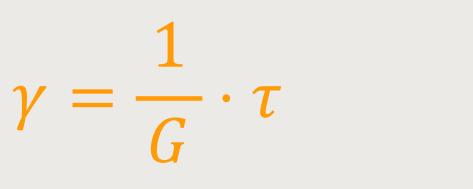
G   ist der Schermodul oder Torsionsmodul

Doch warum nennt man den Scher­modul auch Torsions­modul? Das hat mit der Torsion von Stäben zu tun. Insbe­sondere bei Achsen stellt sich die Frage, welche Dreh­momente über­tragen werden können, bevor ein Körper zu tordieren beginnt. Hierbei könnte man sich gedank­lich einen Stab vorstellen, der aus einzelnen Faser­schichten besteht, ähn­lich wie bei einer Zwiebel. Beim Stab liegen diese Schichten aller­dings konzen­trisch um seine Rotations­achse.

Wenn kein Dreh­moment wirkt, verlaufen die Fasern senk­recht, also parallel zur Dreh­achse. Wirkt dagegen ein Dreh­moment, weil an einem Ende des Stabes eine Umfangs­kraft angreift, dann werden sich die Fasern verschieben. An der Stelle der wirkenden Kraft werden die Fasern um einen Scher­winkel γ geschert. Anderer­seits ergibt sich bezogen auf die Quer­schnitts­fläche ein Torsions­winkel φ.

Zwischen diesen vier vorge­nannten Modulen gibt es zwei allge­meine Relationen, insbe­sondere wenn man isotrope und amorphe Festkörper betrachtet. Wenn es also nicht auf die Richtung inner­halb des Körpers ankommt bzw. wie die entspre­chenden elas­tischen Eigen­schaften sein werden. Die eine Relation beschreibt das Verhältnis zwischen Dehnungs- und Torsions­modul:

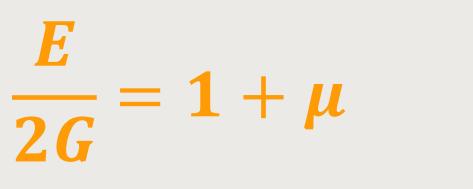
E  ist der Dehnungsmodul
G   ist der Scher- bzw. Torsionsmodul
μ   ist die Poisson-Zahl

Die andere Relation beschreibt das Verhältnis zwischen Dehnungs- und Kompressions­modul:

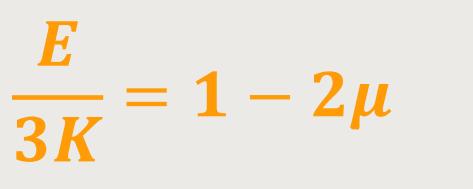
K   ist der Kompressions­modul

Auf diese Art und Weise ist es möglich, ausgehend von zwei Größen, die man relativ leicht ermitteln kann, die fehlenden Größen herzuleiten.

Zwei Material­konstanten sind somit ausreichend, um mit Hilfe der vorge­nannten Relationen das elastische Verhalten von isotropen Fest­körper beschreiben zu können. In der Regel wird man zuerst diejenigen messen, die leicht zu ermitteln sind. Die Größen E und G lassen sich anschlie­ßend mit den Relationen bestimmen.

Natürlich gibt es auch „kristalline Fest­körper”. Und auch da möchte man deren elastische Eigen­schaften beschreiben können. Aller­dings ist es da ein bisschen umständ­licher, wenn ein Kristall beispiels­weise längs oder quer zu einer Kristall­achse gedehnt oder gestaucht werden soll. Da gibt es dann unter­schiedliche Dehnungs­moduln, je nachdem in welche Richtung die Belastung erfolgt.

Man findet auch hier eine Situation vor, ähnlich wie bei der Rotation starrer Köper, bei der man nur mit dem Tensor-Formalismus zu einer Lösung kommt. Denn die Spannungen und die Verzerrungen werden nicht immer parallel sein, sondern unter­schiedliche Richtungen haben. Und eine derartige Relation von Vektoren mit unter­schiedlichen Richtungen, lassen sich nur mit Hilfe von Tensoren sinn­voll darstellen. Dort erhält man als allge­meine Beschreibung des Verzerrungs­zustandes einen Verzerrungs­tensor zweiter Stufe und zusätz­lich zur Darstellung des Spannungs­zustandes einen Spannungs­tensor.

Das Hookesche Gesetz, bei dem es um eine Propor­tionalität mit einer einfachen skalaren Konstanten ging, lässt sich hier nicht anwenden. Daher bezieht am sich im kristallinen Fall sinnvoller­weise auf eine Tensor-Relation. Aber um den Verzerrungs­tensor und den Spannungs­tensor miteinander in Beziehung setzten zu können, benötigt man des Weiteren einen Tensor vierter Stufe (mir 4 Indizes). Das heißt, dieser Tensor hat dann im 3-dimensionalen Raum 81 (3∗3∗3∗3) Komponenten. Das wird schon sehr unüber­sichtlich.

Aber glücklicher­weise gibt es verschiedene Symmetrie­relationen, so dass letzten Endes im allge­meinsten Fall 21 verschiedene Material­konstanten übrig­bleiben. Das sind dann auch die Konstanten, die für das Trikline Kristall­system benötigt werden. Aller­dings, bei den Triklinen gibt es drei Winkel, welche die verschie­denen Kristall­achsen gegen­einander aufweisen. Und drei dieser Konstanten sind bereits diese drei Winkel. Somit bleiben nur mehr 18 andere Elastizitäts­moduln zur Beschreibung des Triklinen Systems übrig.

Triklines System (Kupfersulfat)   21 Konstanten

Neben vielen anderen Systemen gibt es unter anderem auch das kubische Kristall­system.

Kubisches System (Steinsalz)   3 Konstanten

Isotropen Festkörper   2 Konstante

Flüssig­keiten   1 Konstante
Diese eine Konstante ist bei der Flüssig­keit die Kompres­sibilität.

Die Beschrei­bung von Fest­körpern auch im Hinblick auf ihre molekulare Struktur und verschie­denste Eigen­schaften ist ein sehr großes Gebiet in der Physik. Wir beschränken uns jedoch nur auf die elas­tischen Eigen­schaften.

Natür­lich wünscht man sich, alle diese Parameter und diese Moduln auch auf­grund der indivi­duellen moleku­laren Eigen­schaften und Wechsel­wirkungen der verschie­denen Werk­stoffe ausrechnen zu können. Dazu weiß man aber trotz intensiver Bemühungen noch nicht genug, um das mit hinrei­chender Genauig­keit bewerk­stelligen zu können. Nach wie vor ist man für genauere Unter­suchungen auf empirische Konstanten angewiesen.

Jetzt wollen wir noch kurz über die „Härte von Fest­körpern” sprechen. Das ist ein Gebiet, welches sich bis heute kaum quanti­tativ beschreiben lässt. Auch die experi­mentelle Umsetzung gestaltet sich nicht so einfach. Generell ist die Härte ein Maß für den Wider­stand, den ein Fest­körper dem Eindringen eines anderen Fest­körpers entgegen­setzt. Die grund­sätz­liche Frage lautet immer: Bei welcher Kraft wird welche Eindring­tiefe erzielt? Da gibt es beispiels­weise das Ritzungs­verfahren und das oft verwendete Brinell-Verfahren.

Bei dem Brinell-Verfahren betrachtet man eine Stahl­kugel, die mit einer gewissen Kraft in eine Ober­fläche hinein­gedrückt wird. Der Durch­messer der Vertiefung, die dadurch hervor­gerufen wird, ist ein Maß dafür, wie hart die Ober­fläche ist. Das geht natür­lich nicht bei allen Werk­stoffen.

Was man nach wie vor als eine empi­rische Skala verwendet, ist die Härte­skala nach Mohs. Und die reicht von dem aller­weichesten Material „1“ (Talk) bis hin zu „10“ (Diamant). Mittler­weile gibt es ein noch härteres Material als Diamant, nämlich Wurtzit-Bornitrid (ADNR).

Eine weitere Ober­flächen­eigenschaft ist die „Reibung von Fest­körpern”. Bei der Reibung geht es darum, wie die verschie­denen Fest­körper, die längs ihrer Ober­fläche zueinander in Berührung stehen, mit­einander wechsel­wirken.

Man kann sich das so vorstellen, dass beide Festkörper jeweils eine mole­kulare Ober­flächen­struktur haben. Diese Ober­flächen kommen mikros­kopisch gesehen mit­einander in einen solchen Kontakt, dass eine gewisse Kraft benötigt wird, um sie gegen­einander abgleiten zu lassen. Oft verwendet man dabei auch Schmier­mittel, und ein solcher Flüssig­keits­film verringert die Gleit­reibung.

Womit hängt denn die Reibungs­kraft letzt­lich zusammen, wenn man beschreiben möchte, wie stark die Körper aneinander gedrückt werden? Durch Experi­mente lassen sich zwei einfache Zusammen­hänge erkennen. Zum einen ist die Reibungs­kraft die benötigt wird, damit die Ober­flächen aneinander abgleiten können, propor­tional zum Anpress­druck:

Je größer der Anpress­druck zwischen den beiden Ober­flächen ist, umso größer wird propor­tional dazu die Reibungs­kraft sein, die benötigt wird, um die beiden Körper aneinander abgleiten zu lassen. Der zweite Zusammen­hang besteht darin, dass diese Reibungs­kraft auch propor­tional zur Berüh­rungs­fläche ist:

Gibt es eine doppelt so große Berüh­rungs­fläche, wächst auch die Reibungs­kraft in entspre­chender Weise propor­tional an. Wenn das der Fall ist, also dass die Reibungs­kraft, die aufge­wendet werden muss, sowohl propor­tional zum Anpress­druck als auch propor­tional zur Berüh­rungs­fläche ist, dann ergibt sich daraus:

Das heißt wiederum, aufgrund dieser Propor­tionalitäten wird die Reibungs­kraft einfach propor­tional zur Normal­kraft sein, mit der die beiden Werk­stücke zusammen­gedrückt werden.

Man unter­scheidet dann auch noch zwischen „Haft­reibung” und „Gleit­reibung”. Die Haft­reibung muss zunächst einmal über­wunden werden, um das Werk­stück aus dem Ruhe­zustand in Bewegung zu versetzten. Anschlie­ßend ist eine geringere Kraft notwendig, um das Werkstück fortan gleiten zu lassen. Dementspre­chend sehen auch die Beziehungen aus.

Die Haft­reibung wird dadurch beschrieben, dass man eine Haft­reibungs­kraft betrachtet. Das ist eine Kraft, die tangen­tial angewendet werden muss, um den einen Körper gegen den anderen Körper aus anfäng­licher Ruhe in Bewegung zu versetzten:

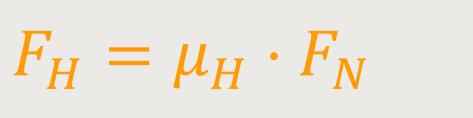
μ_H   ist der Haft­reibungs­koeffizient

Bei der Gleit­reibung ist es der Gleit­reibungs­koeffizient multi­pliziert mit dieser Normal­kraft:

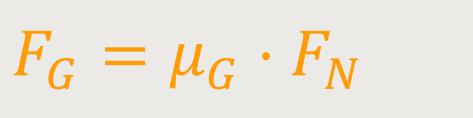
μ_G   ist der Gleit­reibungs­koeffizient

Und schließlich gibt es auch noch die „Roll­reibung”. Das ist aber im eigent­lichen Sinne keine Kraft, sondern vielmehr ein Dreh­moment, welches beim Abrollen eines Körpers ausgeübt wird. Dementspre­chend ergibt sich daraus ein Roll­reibungs­drehmoment:

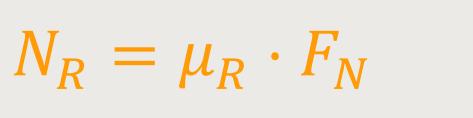
μ_R   ist der Roll­reibungs­koeffizient

Im Gegensatz zu den anderen Koeffi­zienten hat der Roll­reibungs­koeffizient die Dimension [m].

Auch hierzu wurden zahl­reiche Experi­mente durch­geführt, um die Koeffi­zienten für die verschie­densten Materialien zu ermitteln. Aber genauso wie bei den Ober­flächen­eigen­schaften sind das alles nur empirisch ermittelte Werte.

⇦ Kapitel Kapitel ⇨