Bei ruhenden Fluiden spricht man auch von der „Hydro­statik”. Hierbei geht es ins­besondere um die Ober­flächen­eigen­schaften von ruhenden Flüssig­keiten. Die „Hydro­dynamik” folgt im Anschluss.

Bei der Hydro­statik geht es als erstes um den hydro­statischen Druck. In einem Fluid, wie beispiels­weise Wasser, sind die Moleküle bzw. die Volumen­elemente frei verschiebbar. Wenn also von außen Kräfte auf dieses Fluid einwirken, werden sich die verschiedenen Volumen­elemente so lang verschieben, bis ein Gleich­gewicht für das ruhende Fluid eintritt. Die einzelnen Volumen­elemente des Fluids werden sich dann nicht mehr bewegen. Das ist vor allem dann der Fall, wenn die äußeren Kräfte letzt­lich immer senkrecht auf die Ober­fläche des Fluids wirken. Also, die Ober­flächen­kräfte im statischen Fall werden immer senk­recht auf die Ober­fläche des jeweiligen Fluides stehen. Das trifft insbesondere auf Flüssig­keiten zu.

Auf Gase trifft das nicht zu, weil diese im Allge­meinen keine definierte Ober­fläche haben. Es sei denn, man sperrt sie in einen Hohl­körper. Dann gibt es sehr wohl eine Ober­fläche, auf die das Gas von innen einen Druck ausübt. Und wenn ein solches Gleich­gewicht vorherrscht, kann man auch den statischen Druck definieren:

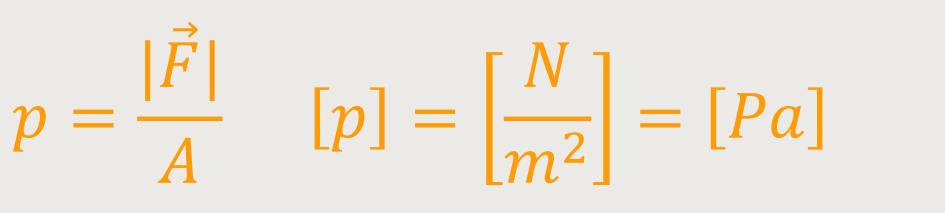
Druck = Kraft / Flächeneinheit

Wenn man die Schwer­kraft vernach­lässigen kann und die inneren Kräfte maßgeblich sind, dann ist im Inneren einer Flüssig­keit die Druck­verteilung homogen und isotrop. Das heißt, im gesamten Fluidum, in welchem die Flüssig­keit oder das Gas vorhanden ist, bleibt der Druck in allen Richtungen gleich.

Aufgrund der Isotropie des Druckes bei statischen Flüssig­keiten und Gasen, gibt es Anwen­dungen in tech­nischen Bereichen. Zum Beispiel hydrau­lische Pressen, hydrau­lische Antriebe, hydrau­lische Bremsen, ja die ganze Hydraulik beruht auf diesem Prinzip. Aber wie sieht es aus, wenn äußere Kräfte wirken? Also, wenn es auch einen Einfluss der Schwer­kraft gibt. Dann kommt es zum soge­nannten „Schwere­druck” in Flüssig­keiten.

Um sich die Wirkung der Gravi­tation als äußere Kraft klar­zumachen, kann man eine Flüssig­keits­säule betrachten. Als Gedanken­spiel bietet sich ein See oder ein Gefäß an, welches mit Wasser gefüllt sind.

Ausgehend von der Wasser­ober­fläche Null bis zu einer gewissen Tiefe t_F gibt es eine soge­nannte Tiefen­achse. Jetzt nimmt man gedank­lich eine Säule dieser Flüssig­keit heraus. Dann schaut man sich in dieser Säule einen kleineren Bereich in einer bestimmten Tiefe t_F und t_F + ΔF an. Es ergibt sich daraus ein Volumen­element in dem Bereich dieser gedachten Säule. In der Tiefe t_F wird natür­lich ein bestimmter Druck p herrschen. Und in der Tiefe t_F + Δt_F herrscht dementspre­chend ein Druck p + Δp. Für den Bereich dieser gedachten Säule ergibt sich ein Volumen ΔV. Das Volumen lässt sich auch beschreiben als Quer­schnitts­fläche · Höhe.

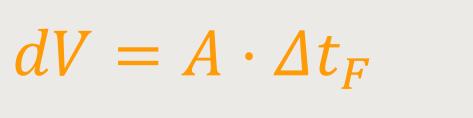
Wie groß ist jetzt das Gewicht dieses Volumen­elements der Flüssig­keit?

Das ist einfach:

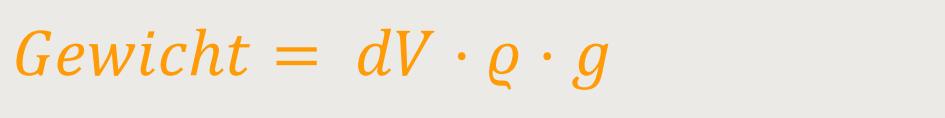
ΔV   ist das Volumen dieses Volumen­elements (Flüssigkeit)
ϱ   ist die Dichte dieser Flüssig­keit
g   ist die Fall­beschleu­nigung

Dieses ermittelte Gewicht bewirkt jetzt die Druckänderung. Denn das Gewicht lastet zusätz­lich auf der unteren Quer­schnitts­fläche. Für die Druck­änderung ergibt sich somit:

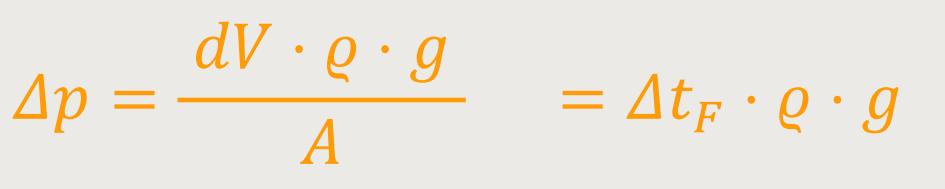
Δt_F   ist die Tiefen­änderung des Fluids

Die Fall­beschleu­nigung ist dabei konstant, und auch die Dichte ist konstant. Weil Flüssig­keiten praktisch inkompres­sibel sind. Der gesamte Druck von der Ober­fläche bis zur bestimmten Tiefe lässt sich durch Summation über alle diese Volumen­elemente bis zu dieser Tiefe ermitteln.

Man braucht zur Berechnung des Druckes nur noch zu integrieren. Hierfür nimmt man ein Integral von dem Ausgangs­druck der Ober­fläche. Das kann zum Beispiel der Atmosphären­druck an der Wasser­ober­fläche sein, bis zu dem höheren Druck in der entspre­chenden Tiefe:

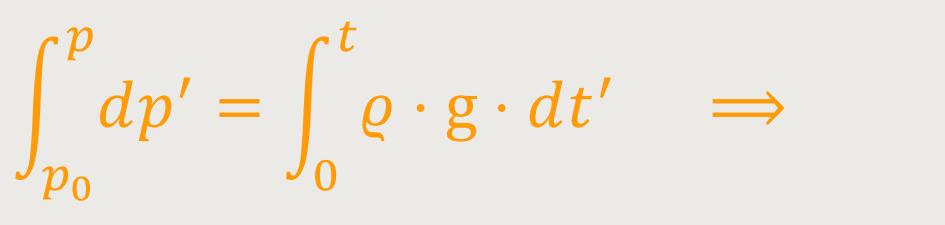
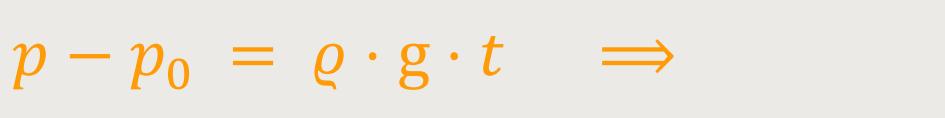
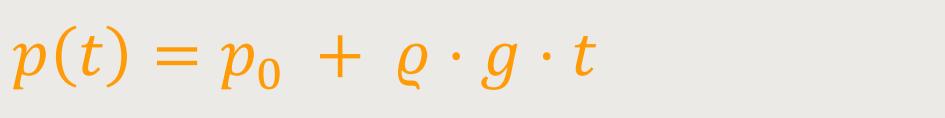
Der Druck nimmt mit der Tiefe linear zu. Das müssen besonders Tief­see­taucher berück­sichtigen, denn beliebig viel Druck hält keine Apparatur aus. Bei Wasser beträgt die Dichte 1000 kg/m³.

Ein Punkt ist aber noch besonders wichtig. Der Druck in einer bestimmten Tiefe t_F hängt nur von der Tiefe und von ein paar einfachen konstanten Parametern wie Dichte und Fall­beschleu­nigung ab. Und aufgrund dessen gibt es ein interes­santes Paradoxon.

Wenn man nämlich verschiedene Gefäße hat, die unter­schied­lich geformt sind, aber alle die gleiche Füll­höhe haben, dann wird der Druck auf die Boden­platte nur von der „Füll­höhe” abhängen. Die Form der Gefäße und das daraus resultierende Volumen bleiben völlig unberücksichtigt.

Das ist der Ausgangs­punkt für das Verständnis der Hydro­statik, mit der wir uns nach­folgend beschäftigen.

Dagegen ist die Situation bei den Gasen etwas anders. Ein wesent­licher Unter­schied besteht darin, dass die Dichte eines Gases nicht immer konstant bleibt. Und damit wird das Integrieren etwas kompli­zierter.

⇦ Kapitel Kapitel ⇨