Der „Schwere­druck” bei Gasen ist nicht ohne Bedeu­tung, denn wir alle bewegen uns in einem Gas. Ohne dieses Gas­gemisch könnten wir nicht exis­tieren. Die Reich­weite dieses Gases geht bis in höhere Sphären hinauf. Und wenn man sich in diese höheren Regionen begibt, wird der Druck immer geringer und das Gas immer dünner. Irgend­wann kann man ohne Hilfs­mittel nicht mehr atmen.

Nach­folgend betrachten wir das Verhalten von Gasen unter dem Ein­fluss der Schwer­kraft.

Wie viel Masse steckt wohl unter Normal­bedingungen in so einem m³ Luft? Wasser hat, wie wir gesehen haben, eine ziemlich große Masse pro Volumen­einheit. Beim Gas liegt die Masse bzw. der Druck bei 1 bar, das ent­spricht etwa 1,293 kg/m³. Obwohl wir das nicht unmittel­bar merken, ist das letzt­endlich doch ein ganz schön ordent­licher Druck, der auf uns lastet.

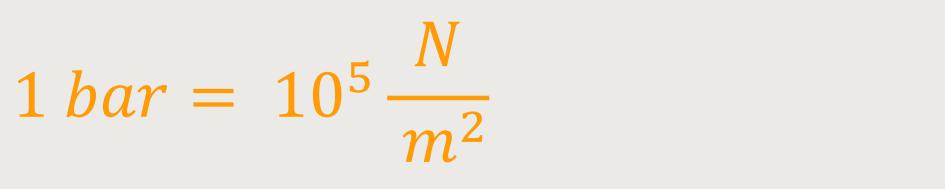
Jetzt wollen wir unter­suchen, wie sich so etwas ausrechnen lässt. Und da verhält es sich ganz analog, wie es bei den Flüssig­keiten der Fall war. Der Unter­schied ist nur, dass wie bereits erwähnt die Dichte nicht konstant ist. Flüssig­keiten verzeichnen unter Druck keine nennens­werte Verän­derung der Dichte. Das liegt an der sehr geringen Kompres­sibili­tät von Flüssig­keiten. Gase hingegen, wozu auch die uns umge­bende Luft gehört, lassen sich sehr wohl kompri­mieren.

Um das ausrechnen zu können, müssen wir ein bisschen auf die Thermo­dynamik vorgreifen. In der Thermo­dynamik gibt die soge­nannte „Zustands­gleichungen” idealer Gase. Und die Luft ist in guter Näherung ein ideales Gas. Der Aspekt, der zunächst für uns wichtig ist, hat mit einer konstanten Temperatur zu tun. Gesetzt den Fall, in dem System herrscht eine konstante Temperatur, gibt es das Boyle-Mariottesche Gesetz. Das ist ein sehr wichtiges Gesetz und lautet:

Mit anderen Worten, wenn man den Druck verdoppelt, wird das Volumen halb so groß. Im Allge­meinen kann man davon ausgehen, dass in jedem Teilsystem, welches man unter­sucht, die Masse gleich bleibt m = const. Das bedeutet:

ϱ   ist Masse · Volumen­einheit

Also, wenn das Volumen halb so groß ist, wird die Dichte doppelt so groß. Damit ist p · V = const, und es folgt daraus:

Somit lässt sich schluss­folgern, dass es an einer bestimmten Stelle, zum Beispiel am Erdboden, einen gewissen Referenz­druck und eine gewisse Referenz­dichte gibt. Mittels dieser Referenz­werte lassen sich der Druck und die Dichte ermitteln. Damit erhält man:

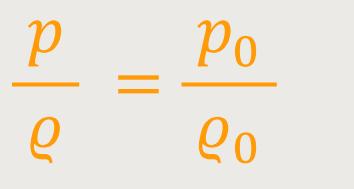
Und letztlich lässt sich die Dichte ausrechnen:

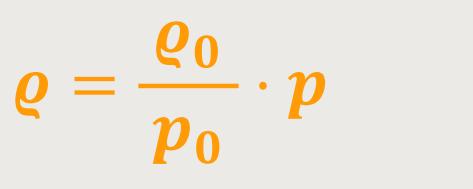
Mit dieser einfachen Beziehung wird die Dichte als Funktion des Druckes definiert. Voraus­gesetzt wir haben es mit einer konstanten Temperatur zu tun. Um das im Einzelnen berechnen zu können, benötigt man analog wie beim Wasser in diesem Fall eine Gas-Säule. Man betrachtet zwar die gesamte Atmos­phäre, greift aber gedank­lich nur ein säulen­förmiges Stück heraus. Anschlie­ßend wird unter­sucht, welcher Zusammen­hang besteht.

h   ist die Höhe dieser Gas-Säule
A   ist die Querschnitts­fläche

Diesmal fängt man vom Boden­niveau an. Man unter­sucht in einer solchen Säule wieder einen bestimmten Höhen­abschnitt h. Am Boden befindet sich die Höhe Null. Der Höhen­abschnitt wird definiert von h bis h + Δh. Bei der unteren Abschnitts­fläche in diesem Höhen­abschnitt herrscht ein Druck p. Und an der oberen Fläche entspre­chend ein Druck p + Δp. Wobei man damit rechnen muss, dass dieses Δp negativ sein wird, weil der Druck ja mit der Höhe abnimmt. Am Boden gibt es den Referenz­druck p_₀. Und das Volumen dieses Höhen­abschnitt ist gegeben als dV.

Das Volumen ergibt sich ähnlich wie bei Flüssig­keiten:
dV = A · Δh

Und damit ist die Geometrie für die Gas-Säule festgelegt. Wie wird sich der Druck ändern, und wodurch ändert er sich? Nun, zunächst einmal hat dieser Abschnitt inner­halb der Gas-Säule auch wieder eine gewisse Masse und damit auch ein gewisses Gewicht. Aufgrund des zusätz­lichen Gewichts dieses Höhen­abschnitts, wird auch hier der Druck an der unteren Quer­schnitts­fläche zunehmen.

Das Gewicht dieses Volumen­elements ist definiert als:

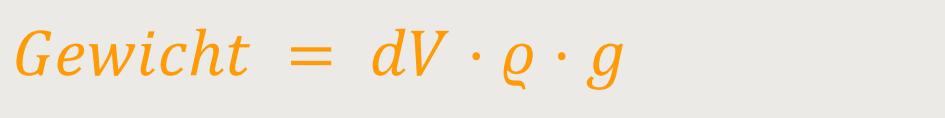
dV   ist das Volumen dieses Volumen­elements des Gases
ϱ   ist die Dichte dieses Gases
g   ist die Fall­beschleu­nigung

Masse = Dichte · Volumen
Gewicht = Masse · Fall­beschleu­nigung

Dieses Gewicht bewirkt jetzt die Druck­änderung. Denn das Gewicht lastet zusätz­lich auf der unteren Quer­schnitts­fläche. Für die Druck­änderung ergibt sich demnach:

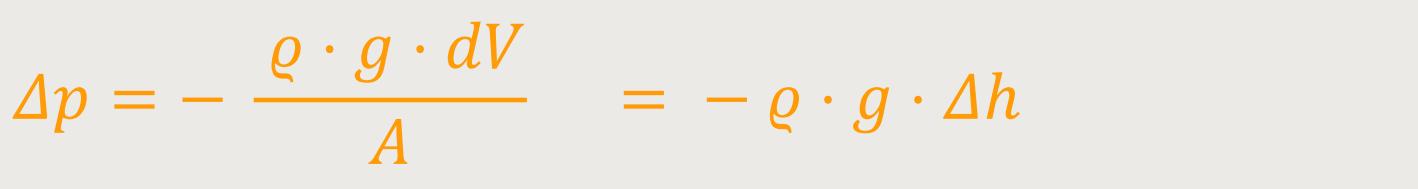
Δh   ist die Höhen­änderung des Gases

Der Zusammenhang mit der Druck­abhängig­keit stellt sich wie folgt dar:

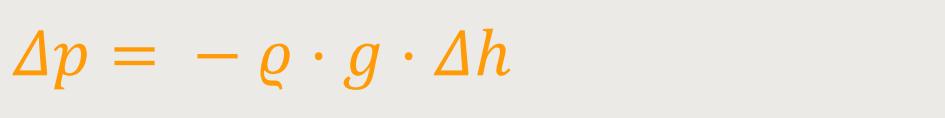
Anders als bei Flüssig­keiten ist die Dichte hierbei nicht konstant. Denn die Dichte eines Gases ist abhängig vom Druck.

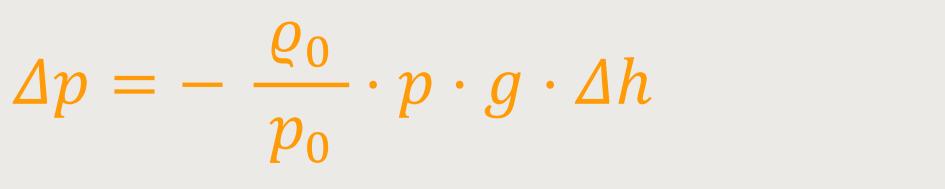
Man kann schon erkennen, dass man hier eine Differenzial­gleichung erhält. Da der Druck variabel ist, müssen wir deshalb anders vorgehen. Zunächst führt man eine Trennung der Variablen durch. Weshalb ist das wichtig?

Weil es sowohl eine abhängige als auch eine unabhängige Variable gibt. Unabhängig ist die Höhe h. Abhängig ist aber der Druck p. Man möchte ja wissen, wie h mit p zusammen­hängen. Trennung heißt, der Druck p muss in der Gleichung auf die andere Seite:

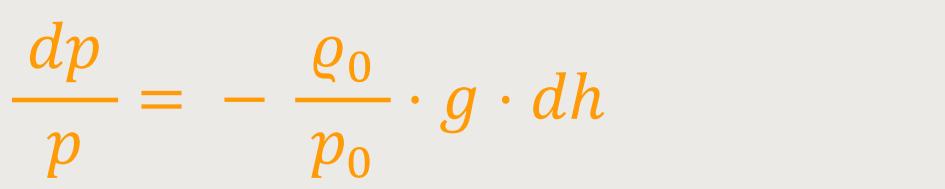
− (ϱ₀ / p₀) · g   ist wieder eine Konstante

Zur Berechnung des Drucks muss man jetzt nur noch integrieren. Hierzu nimmt man ein Integral des Ausgangs­druckes der Ober­fläche. Das kann zum Beispiel der Atmos­phären­druck am Erd­boden sein, bis zu dem geringeren Druck in der entspre­chenden Höhe:

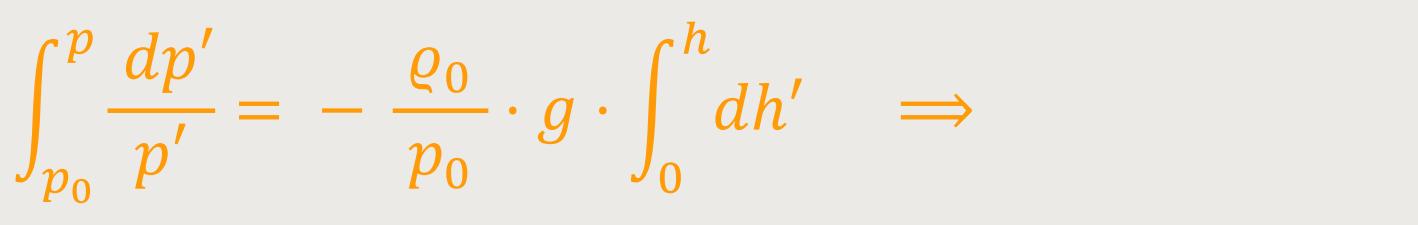
Das Integral dp' / p' ist ln.

Somit kommt ein logarithmus naturalis mit in die Gleichung herein:

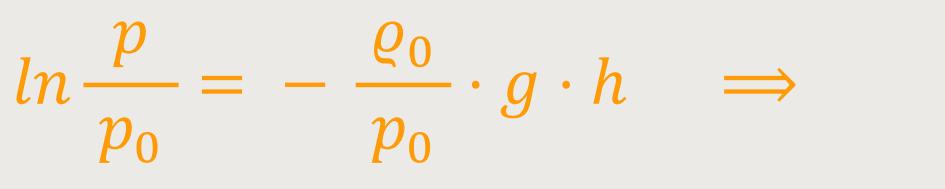
Anschlie­ßend wird eine Exponen­zierung | exp auf beiden Seiten der Gleichung durch­geführt:

Nach Umformen erhält man:

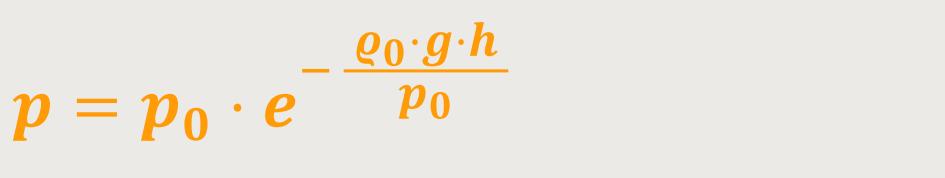
Und das ist die berühmte Baro­metrische Höhen­formel.

Mit dem Baro­meter misst man bekannt­lich den Luft­druck. Aber wie muss man sich das konkret vorstellen? Aus dieser Formel ergibt sich, dass zwischen der Höhe und dem Druck kein linearer Zusammen­hang besteht. Insofern ist es hilf­reich, insbe­sondere für die Atmos­phäre entspre­chende Zahlen­werte mit anzugeben.

Damit das Ganze etwas greifbarer wird, hier einige Werte aus unserer Atmosphäre:

Einen Druck­abfall auf p₀ /2 erreicht man in 5,8 km Höhe. Wenn man aber einen Druck­abfall auf p₀ /4 erreichen möchte, muss man schon auf 11,5 km aufsteigen. Bei Flüssig­keiten hört der Druck an der Ober­fläche einfach auf.

Bei der Atmos­phäre ist das nicht so, sie wird nach oben hin immer dünner. Es gibt einen kontinuier­lichen Über­gang, solange bis sich kein Druck mehr messen lässt. In diese Höhen kann man sich nur noch forma­listisch fragen: In welcher Höhe geht der Druck um wie viel zurück? Die Gase haben unter Einwirkung der Schwer­kraft keine definierte obere Grenze.

Ein weiterer wichtiger Punkt, den wir betrachten wollen, ist das Phänomen des Auftriebs.

⇦ Kapitel Kapitel ⇨