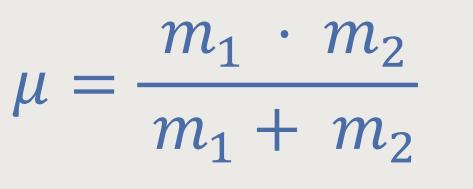Streuvor­gänge sind ganz wichtig zur Unter­suchung von Struk­turen im Mikro­kosmos, also wenn es um die Struk­turen von Atomen und Atom­kernen geht. Oft kann man nur mithilfe von Streu­experi­menten struk­turelle Infor­mationen über diese kleinen Systeme gewinnen. Hierzu schießt man Teilchen auf die jewei­ligen Atomkerne.

Auf diese Weise hatte zum Beispiel Ernest Rutherfort im Jahre 1911 erst­mals die Struktur eines Atoms und die Existenz eines Atom­kerns nach­weisen können. Dies konnte er durch Streuung von Alpha­teilchen an den Gold­atomen einer Gold­folie beobachten. Und auch heute noch, wo man die Struktur verschiedener Elementar­teilchen und ihre Wechsel­wirkungen mittels Hoch­energie­experimenten unter­sucht, ist es gang und gäbe Streu­experimente durch­zuführen. Im Bereich der klassischen Mechanik betrachtet man jeweils zwei Massen­punkte oder Teilchen.

Wesent­lich dabei ist, dass diese zwei Massen­punkte nur in einem relativ begrenzten Bereich nennens­wert mitein­ander wechsel­wirken. Das ist zum Beispiel dann der Fall, wenn beide Teilchen im Begriff sind, mitein­ander zu kolli­dieren. Eines dieser beiden Teilchen wird also auf das andere einfallen. Das eine nennt man dementspre­chend das „einfallende Teilchen” und das andere das „Target-Teilchen”.

Nur wenn sich beide Teilchen genü­gend nahe kommen, kommt es zu einer nennens­werten Wechsel­wirkungs­kraft und damit zu entspre­chenden Beschleu­nigungen. Außerhalb des Wechsel­wirkungs­bereiches bewegen sich die Teilchen mit konstanter Geschwindig­keit, voraus­gesetzt es wirken keine anderen äußeren Kräfte.

Den Verbindungs­vektor vom Target-Teilchen m_₂ zum einfal­lenden Teilchen m_₁ nennt man _{₁ ₂}. Das ist der Relativ­vektor, der die beiden Teilchen im Wechsel­wirkungs­bereich jeweils verbindet.

Eine weitere wichtige Größe ist der soge­nannte „Streu­winkel” ϑ_₁. Hierbei betrachtet man nur den Winkel der Bewegungs­richtung des einfallenden Teilchens vor und nach dem Stoß. Der Streu­winkel beschreibt damit die Richtungsänderung des einfallenden Teilchens. Seine Richtungs­änderung hat mit der Richtung des Target-Teilchens nicht unmittel­bar etwas zu tun.

Um eine Unter­scheidung zwischen dem einfallendem Teilchen und dem Target-Teilchen heraus­zustellen, wählt man spezielle Bezugs­systeme. Letztlich betrachtet man ein und denselben Vorgang aus der Sicht unter­schied­licher Bezugs­systeme.

Nan wählt dabei „Spezielle Bezugs­systeme”, die es einem gestatten, Streuvor­gänge mög­lichst einfach darzu­stellen. Eines dieser Bezugs­systeme ist das Labor­system. Das Labor­system ist einfach dadurch fest­gelegt, dass sich das Target-Teilchen vor dem Stoß in Ruhe befindet. Daraus ergibt sich:

Außer­halb des Wechsel­wirkungs­bereiches bewegen sich die Teilchen vor dem Stoß gleich­förmig gerad­linig. Damit ist das Labor­system ein sogenanntes Inertialsystem.

Hinweis: Der Impuls eines Körpers hängt davon ab, in welchem Bezugs­system man ihn betrachtet. In dem einen Bezugs­system kann sich ein Körper in Ruhe befinden. Dann hat der Körper den Impuls gleich Null. Wenn man denselben Körper aber aus der Sicht eines bewegten Bezugs­systems anschaut, dann wird sich der Körper relativ zum bewegten System eben­falls bewegen und hat in diesem Fall einen Impuls. In jedem der gewähl­ten Bezugs­systeme wird der Impuls­erhaltungs­satz jeweils für sich gelten. Denn die Impulse müssen vorher und nachher überein­stimmen. Aber wie groß die jewei­ligen Impulse sind, hängt immer davon ab, was für ein Bezugs­system man wählt.

Wenn man nun obiges Labor­system betrachtet, dann ist der Impuls des Target-Teilchens vor dem Stoß gleich Null. Bei Labor­experimenten ist es meistens so, dass sich das Target-Teilchen vor dem Stoß in Ruhe befindet, und daher keinen Impuls hat. Nach dem Stoß werden die Impulse beider Teilchen in Summe dem Impuls des ursprüng­lich einfallenden Teilchens entsprechen.

Im Labor­system kann man auch den soge­nannten Stoß­parameter b definieren. Der Stoß­parameter ist die Distanz, um die das einfallende Teilchen das Traget-Teilchen quasi verfehlt. Man könnte auch sagen, es ist der Normal­abstand des Target-Teilchens zur Bewegungs­geraden des einfallenden Teilchens vor dem Stoß.

Eine weitere wichtige Größe ist die Bahn des Schwer­punktes. Wenn zum Beispiel die Massen der beiden Teilchen gleich groß sind, dann wird der Massen­mittelpunkt immer beim halben Normal­abstand zwischen den beiden Einzel­massen liegen. Zudem bewegt er sich gleich­förmig gerad­linig entsprechend dem Erhaltungs­satz für den Massen­mittel­punkt­impuls. Voraus­gesetzt natürlich, es wirken außer­halb des Wechsel­wirkungs­bereiches keine weiteren äußeren Kräfte.

Den Verbindungsvektor vom Target-Teilchen zum einfallenden Teilchen nennt man auch hier wieder _{₁ ₂}.

Dieser Relativ­vektor verbindet nach wie vor das Target-Teilchen mit dem einfallenden Teilchen, und kippt während des Verlaufs der Bewegung um einen gewissen Winkel. Wenn beide Teilchen nach dem Stoß den Wechsel­wirkungs­bereich verlassen haben, bleibt der Relativ­vektor in seiner neuen Ausrichtung. Und zwar solange, wie die beiden Teilchen mit konstanter Geschwindig­keit auseinander­streben.

Die bisher betrachtete Darstellung ist aller­dings nicht besonders günstig, weil sich beide Massen­punkte in Bewegung befinden. Günstiger wäre es, wenn man hierbei ein sogenanntes Zweikörper­problem betrachten könnte, und man sich als Beobachter in einem Bewegungs­zustand befindet, wo der Massen­mittel­punkt in Ruhe ist. Um das zu erreichen, muss man wieder in ein anderes Bezugs­system transformieren.

Um zu erreichen, das der Massen­mittel­punkt in Ruhe ist, trans­formiert man in ein anderes Bezugs­system, das sogenannte „Massen­mittel­punkt­system”.

Der Massen­mittel­punktort ist definiert als:

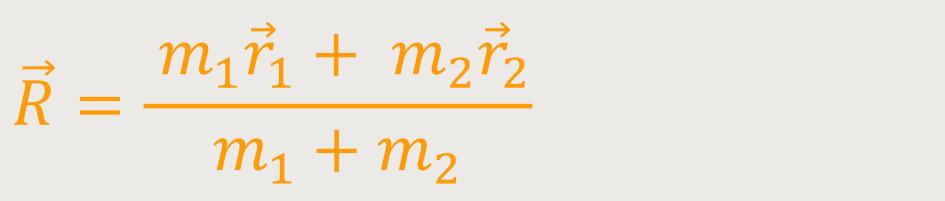
Diese Beziehung kennen wir bereits aus der Erhaltung des Massen­mittel­punkt­impulses.

Andererseits kann man auch definieren, wie sich dieser Massen­mittel­punkt bewegen wird:

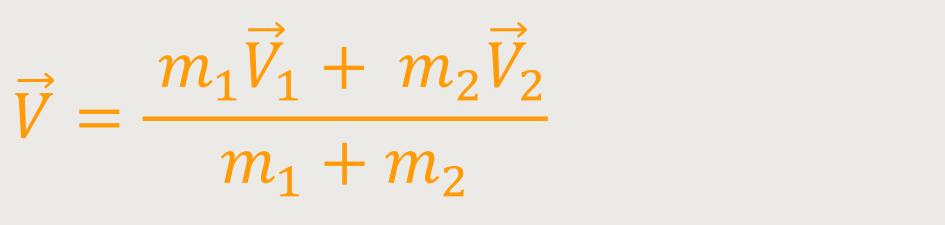
Hier setzt man aller­dings voraus, dass im Massen­mittel­punkt­system bzw. im Schwer­punkt­system gleich Null ist:

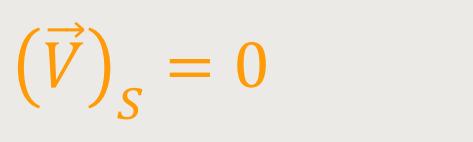
Was bedeutet das? In obigem Fall spielt der Nenner keine Rolle. Somit erhält man durch Umformen:

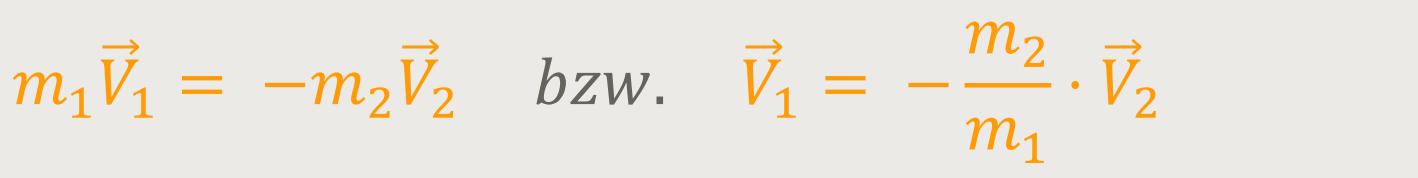
Das heißt, im Schwer­punkt­system wird es so sein, dass die Geschwindig­keit des einfallenden Teilchens und die Geschwindig­keit des Target-Teilchens immer parallel und zugleich entgegen­gesetzt zueinander sind. Denn sonst könnte auch der Massen­mittel­punkt nicht in Ruhe verharren. Und weil in ein anders Bezugs­system trans­formiert wurde, ist das Target-Teilchen vor dem Stoß in diesem Fall nicht in Ruhe.

Wie sieht also jetzt dieselbe physika­lische Situation aus Sicht des Schwer­punkt­systems aus?

Nehmen wir an, das einfallende Teilchen kommt von links und das Target-Teilchen kommt von rechts aus entgegen­gesetzter Richtung. Auf der Hälfte des Normal­abstandes gibt es eine gedachte Achse, und zwischen beiden Teilchen befindet sich an konstanter Position der Schwer­punkt. Nun kommen beide Teilchen aufein­ander zu, und lenken sich im Wechsel­wirkungs­bereich gegen­seitig ab. Wesent­lich bei der nach­folgenden Betrachtung ist, dass sich beide Teilchen nach dem Stoß wieder diametral, parallel und entgegengerichtet fortbewegen.

Hierbei „dreht” sich der Relativvektor _{₁ ₂} während des Stoßes um einen gewissen Winkel herum. Über eine längere Distanz gesehen entspricht der Schwenk­winkel des Relativ­vektors auch dem Streu­winkel Θ im Schwer­punkt­system.

Bei der Gegen­über­stellung kann man deutlich erkennen, dass der Streu­winkel in unter­schied­lichen Bezugs­systemen unter­schiedliche Werte hat.

Θ ist der Winkel zwischen den Relativ­vektoren. Und die Relativ­vektoren verhalten sich unabhängig vom Bezugs­system. Das ist nichts anderes als der Verbindungs­vektor von einem zum anderen Teilchen.

Damit gilt:

(_₁ )_s ist die Relativ­geschwindig­keit relativ zum ruhenden Schwerpunkt.

Mit Bezug auf das Labor­system bedeutet das:

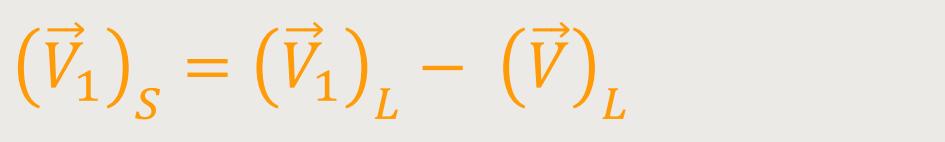
Die Relativ­geschwindig­keit muss in jedem System die gleiche sein. Daraus folgt:

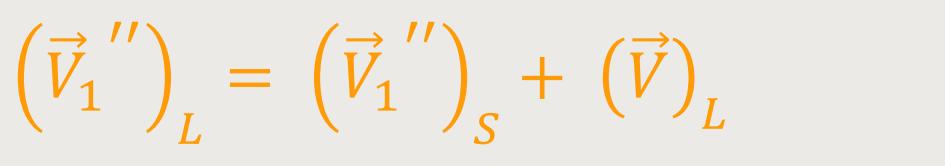
Also, die einfallende Geschwindig­keit im Labor­system ist gleich der einfallenden Geschwindig­keit im Schwer­punkt­system zuzüg­lich der Geschwindig­keit des Schwer­punktes. Das gilt insbe­sondere nach dem Stoß (_₁^" ).

Der Streu­winkel im Schwer­punkt­system ist immer ≥ dem Winkel im Labor­system, weil das Target-Teilchen im Labor­system ruht. Betrachtet man aber den gleichen Vorgang aus Sicht des Schwer­punkt­system, bewegen sich die Teilchen bereits verlang­samt, und wenn ihnen dann noch etwas entgegen fliegt, werden sie stärker abgelenkt und damit ist der Streu­winkel Θ immer ≥ gegen­über dem Streu­winkel ϑ₁ .

Damit erhält man als Ergebnis für elastische Stöße:

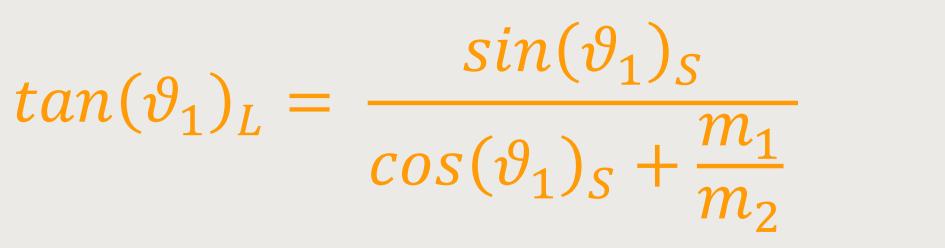
So lässt sich der Zusammen­hang zwischen den Streu­winkeln darstellen. Man nennt dies auch die „Trans­formations­formel für Streu­winkel”.

Es kommt bei dem Zusammen­spiel wesent­lich auf das Verhält­nis zwischen den beiden Massen m_₁ und m_₂ an.

Wenn das Target-Teilchen eine viel größere Masse hätte als das einfallende Teilchen, dann stimmen beide Bezugs­systeme inhalt­lich überein. Wenn die Massen dagegen gleich sind, kommt man nur auf einen maximalen Streu­winkel von 90°.

Jetzt kann man noch einen Schritt weiter gehen, um von einen Zweikörper­system auf ein Einkörper­system mit reduzierter Masse über­zugehen. Denn jedes Zweikörper­system lässt sich formal zurück­führen auf die Dynamik eines Einkörper­problems. Hierbei bewegt sich eine reduzierte Masse im Feld der Wechsel­wirkungs­kräfte, und der Orts­vektor dieser reduzierten Masse ist dann, über­tragen auf die Streu­vorgänge, der Relativ­vektor.

Die reduzierte Masse hatten wir ja bereits definiert als:

Die Idee ist, dass man den Streu­vorgang in eine Bewegung einer reduzierten Masse μ über­setzt, die sich in dem Feld der Wechsel­wirkungs­kräfte bewegt. Wobei die Wechsel­wirkungs­kräfte meistens konservative Kräfte sind, also keine Reibungs­kräfte. Man hat es vielmehr mit Kräften zu tun, die sich als Gradienten eines Potentials darstellen lassen. Daher spricht man auch in einem solchen Fall von Potential­streuung.

Der konkrete Verlauf eines solchen Streu­vorgangs hängt ganz wesent­lich davon ab, was für ein Potential der Wechsel­wirkung zwischen den beiden Teilchen vorhanden ist. Und in der Über­setzung des reduzierten Einkörper­problems lässt sich dieses Potential visuali­sieren in Form eines Potential­gebirges.

Das reduzierte Einkörper­problem funktio­niert so, dass man nur noch eine einzige Masse μ betrachtet, in der die beiden Einzel­massen enthalten sind. Und diese reduzierte Masse bewegt sich im Feld der Wechsel­wirkungs­kraft, darge­stellt durch ein solches Potential­gebirge. Daher rührt auch der Begriff „Potential­streuung”, wobei der Orts­vektor zugleich der Relativ­vektor ist. Dieses reduzierte Einkörper­problem muss dann, wenn man das realistisch umsetzten möchte, in den konkreten wirk­lichen Vorgang rück­übersetzt werden. Dabei berück­sichtigt man, wie das Massen­verhältnis der beiden Teilchen ist. Der Streu­winkel bei der reduzierten Masse ist gleich dem Streu­winkel des Massen­mittel­punkts, also im Schwer­punkt­system.

Wenn man dann aber auf die Labor­bedingungen Rück­schlüsse ziehen will, um die Dinge konkret mit einem experimen­tellen Befund vergleichen zu können, muss man diesen Streu­winkel zurück über­setzen in den allgemein kleineren Streu­winkel im Labor­system. Dann erhält man etwas, was wirklich mit dem Experiment verglichen werden kann. Und es hängt letztlich davon ab, ob das Ganze zusammen­passt. Wenn es stimmig ist, dann ist das ein starkes Indiz dafür, dass das gewählte Potenzial den konkreten Bedingungen annähernd entspricht.

Auf die Art und Weise kann man durch so ein Streu­experiment in einer indirekten Weise auf die Verhält­nisse in dem unmittel­baren Streu­bereich Rück­schlüsse ziehen. Der jeweilige Streu­winkel hängt sowohl von den Stoß­parametern als auch von der Energie des einfallenden Teilchens ab. Aus diesen Parametern lässt sich eine Ablenk­funktion herleiten.

Man geht davon aus, dass es in der Umgebung eines kleinen massiven Atomkerns ein Wechsel­wirkungs­potential gibt. Und zwar elektrische Punkt­ladungen, die einander abstoßen.

Die Ablenk­funktion ist definiert als:

Θ   ist der Streu­winkel im Schwer­punkt­system
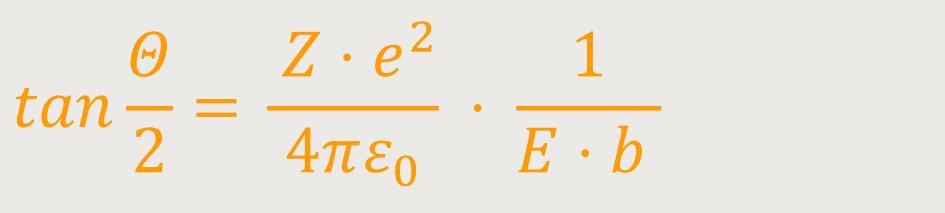
Z   ist die Kernladungs­zahl
e   ist die Elementar­ladung (eines Elektrons o. Protons)
ε   ist ein Theorie­faktor in der Elektro­dynamik
E   ist die Teilchen­energie des einfallenden Teilchens
b   ist der Stoß­parameter
4πε₀ = const   ist eine Konstante

Und nachdem man diese Ablenk­funktion auch gut experi­mentell über­prüfen konnte, hält man bis heute an dem Rutherfordschen Atommodell fest.

⇦ Kapitel Kapitel ⇨