Wir sind immer noch im Kapitel deformier­bare Körper. Jetzt wenden wir uns den „Fest­körpern” zu. Bei Fest­körpern ist es so, dass äußere Kräfte, die an einem Fest­körper angreifen dazu führen, dass sich dieser verformt. Die äußeren Kräfte greifen an der Ober­fläche des Körpers an und bewirken, dass er defor­miert wird. Man spricht dabei nicht von Volumen­kräften, wie zum Beispiel die Schwer­kraft, die ins Innere eines Körpers wirkt. Auch noch von magne­tischen Kräften, die auf ferro­magnetische Werk­stoffe im Innern hinein­wirken. Bei den elas­tischen oder auch plas­tischen Verfor­mungen von festen Körpern betrachten wir nur Ober­flächen­kräfte.

Daher ist es sehr wichtig, diese Kräfte auf eine Flächen­einheit zu beziehen. Eine solche Kraft pro Fläche könnte beispiels­weise als Druck aufge­fasst werden. Aber auch hierbei kann es um Kräfte gehen, die schräg oder sogar tangen­tial an die Ober­fläche eines Körpers angreifen. Daher werden die Kräfte nicht einfach nur als Drücke bezeichnet. Denn eine Kraft kann sich auch als Zugkraft erweisen. Aber um keine Verwirrungen hervor­zurufen, verwendet man generell den Ausdruck „Spannung”.

Spannung = Kraft pro Flächeneinheit

Eine Kraft wird aber nicht nur senkrecht auf eine Fläche wirken. Spannungen lassen sich je nach Wirkungs­weise unter­teilen in Normal­spannungen und Tangential­spannungen. Unter Normal­spannungen versteht man solche, bei der die Kraft senk­recht auf die jeweilige Ober­fläche wirkt. Bei Tangential­spannungen dagegen wird die äußere Kraft tangential angreifen. Solche Spannungen nennt man auch „Scher­spannungen”. Derartige Spannungen werden üblicher­weise mit τ (tau) bezeichnet.

Bei der Normal­spannung unter­scheidet man noch­mals zwischen Zug- und Druck­spannung. Die Zug­spannung wir mit σ (sigma) bezeichnet und die Druck­spannung mit p. Alle diese Größen haben alle die gleiche Dimension, nämlich N /mm². In Fach­büchern für den Maschinen­bau finden sich aber auch Bezeichnungen wie σ_z für Zug­spannung und σ_d für Druck­spannung.

Jetzt werden wir kurz betrachten, auf welche Weise verschiedene Körper deformiert werden können. Anschließend fragen wir nach der Ursache von solchen Defor­mationen. Und dort spielen diese Spannungen eine wesent­liche Rolle mehr. Ein wichtiger Punkt ist nämlich die Frage, wie hängt die Größe der Spannung mit der Stärke der Deformation zusammen? Das führt letzt­lich zu den wichtigen Gleichungen in der Elastizitäts­lehre. Doch zunächst sprechen wir allgemein über Deformationen.

„Deformationen” lassen sich auf zweierlei Weise charakte­risieren. Die erste Möglich­keit ist, ein fester Körper deformiert sich so, dass sich sein Volumen ändert aber seine Gestalt erhalten bleibt. Zum Beispiel ein Würfel, der von allen Seiten gleich­mäßig etwas zusammen­gedrückt wird. Die Volumen­änderung ergibt sich dann aus dem End­volumen minus das Anfangs­volumen:

Wenn der Würfel durch eine äußere Druck­spannung all­seitig zusammen­gedrückt wird, wird das Volumen zwangs­läufig kleiner werden. Somit wird dieses ΔV negativ sein. Dazu lässt sich auch noch die relative Volumen­änderung definieren:

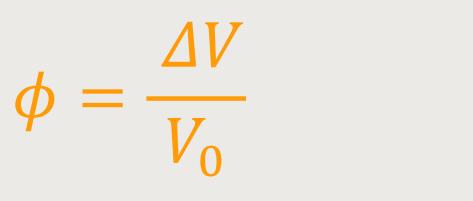
ϕ   ist die relative Volumen­änderung

Die relative Volumen­änderung ist eine prozen­tuelle Änderung des Volumens durch eine äußere Kraft­wirkung.

Als zweite Möglich­keit kann man die Gestalt des Körpers verändern, ohne sein Volumen zu ändern. Nehmen wir wieder diesen Würfel. Diesmal ist er auf einem Unter­grund fixiert. Und an der Ober­fläche wirkt tangential eine Kraft in seit­liche Richtung, man spricht auch von einer „Scher­kraft”. Der Körper verformt sich dann zu einem Parallelo­gramm, wobei das Volumen erhalten bleibt.

Die Verzerrung der senk­rechten Flächen zur Seite hin ergibt den Scher­winkel γ. Somit beschreibt dieser Scher­winkel die Gestalt­änderung. In vielen Fällen wird aber beides zugleich auftreten, eine Volumen­änderung und eine Gestalt­änderung. Das passiert beispiels­weise dann, wenn man einen länglichen Stab einseitig belastet, indem man ihn dehnt oder staucht.

Hierzu denken wir uns einen Stab, der an einer Wand befestigt ist. Und jetzt greift an der Stirn­fläche eine Kraft an, die den Stab in die Länge zieht. Die ursprüng­liche Länge L_₀ verändert sich zur gedehnten Länge L. Die Ände­rung der Länge wird durch das ΔL definiert. Ander­seits verändert sich auch der Quer­schnitt. Der Ausgangs­durchmesser d_₀ verändert sich zum gedehnten Durch­messer d, indem er schlanker wird. Man nennt so etwas die „Quer­kontraktion”.

Die Quer­kontraktion hängt mit der Längen­änderung zusammen. In diesem Zusammen­hang werden wir zwei verschiedene Größen betrachten. Einer­seits die Größe ε (epsilon), das ist die relative Längen­änderung:

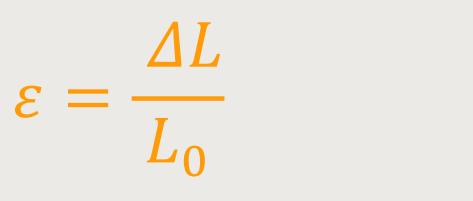
Die relative Längen­änderung ist eine prozen­tuelle Ände­rung der Länge durch eine äußere Kraft­wirkung. Die gleiche Kraft führt bei verschie­denen Stäben mit unter­schied­lichen Ausgangs­längen zu unter­schied­lichen absoluten Ausdeh­nungen ΔL. Aber die relative Längen­änderung wird in diesen Fällen immer die Gleiche sein.

Und als zweite Größe ist die relative Quer­kontraktion sehr wichtig, die wie folgt definiert wird:

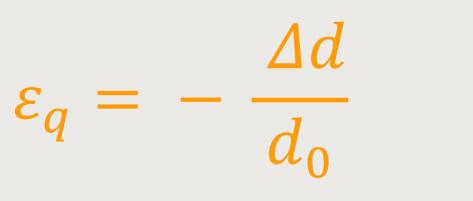
Denn wenn sich die Länge ändert und größer wird, dann wird zugleich der Quer­schnitt geringer werden. Diese relative Quer­kontraktion führt uns zu einer weiteren wichtigen Größe, nämlich zu der berühmten Poisson-Zahl.

Es erhebt sich nämlich die Frage, wie diese beiden relativen Ände­rungen mit­einander zusammen­hängen? Die Auswir­kungen hängen natür­lich auch vom Werk­stoff des Körpers ab.

Deshalb definiert man sich zusätz­lich eine Größe μ, bei der es sich wieder um eine dimensions­lose Zahl handelt.
Die Poisson-Zahl wird definiert als:

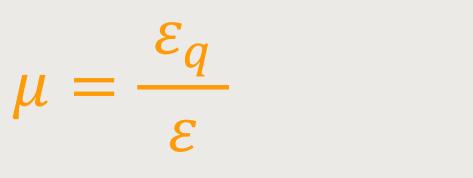
Die Poisson-Zahl ist charakte­ristisch für das Verhalten eines verform­baren Fest­körpers bei ein­seitiger Dehnung oder Stauchung. Da die Poisson-Zahl das Verhältnis der relativen Quer­dimensions­änderung zur relativen Längs­dimensions­änderung angibt, erhält man eine Aussage darüber, wie sehr sich das Volumen dieses einseitig gedehnten Stabes ändern wird. Das Verhältnis wird logischer­weise nicht konstant bleiben.

Wenn man das durch­rechnet, lässt sich die relative Volumen­änderung wie folgt darstellen:

ϕ   ist die relative Volumen­änderung (s.o.)

Jetzt interes­siert uns noch, wie man die Ursachen dieser Verzer­rungen beschreiben kann, oder wie sie mit­einander in Beziehung stehen. Die Frage ist daher, welche Spannungen bewirken welche Verzerrungen? Und dazu eignet sich besonders gut das soge­nannte Spannungs-Dehnungs­diagramm. Um sich das anschau­lich vorzu­stellen, denken wir uns einen länglichen Stab, der durch die Wirkung einer in der Quer­schnitts­fläche angrei­fenden Kraft ausgedehnt wird. Eine solche Betrachtungs­weise ist immer der Ausgangs­punkt in der Elastizitäts­lehre.

Es gibt einen wesent­lichen Unter­schied zwischen elas­tischen und plas­tischen Verformungen. Bei einer elas­tischen Ver­formung kehrt der Körper wieder in seine Ausgangs­situation zurück. Bei einer plas­tischen Verformung bleibt der Körper im gedehnten Zustand, auch wenn keine Kraft mehr wirkt. Im Extrem­fall, wenn die Elastizitäts­grenze über­schritten ist, kann es sogar zum Bruch kommen.

Grundsätzlich haben wir im „Spannungs-Dehnungs-Diagramm” zunächst einen Bereich, in welchem der Körper propor­tional gedehnt wird, nämlich der Propor­tionalitäts­bereich. Und der geht linear bis zur Propor­tionalitäts­grenze. Dann schließt sich ein nicht linearer Bereich an, der aber trotzdem noch elas­tisch ist. Der Körper wird sich bei Nach­lassen der Kraft noch zurück­bilden. An dieser Stelle befindet sich die Fließgrenze. Jenseits dieser Grenze beginnt das Material zu fließen, und es gelangt nicht mehr in seine ursprüngliche Situation zurück. Bis es dann letztlich bei der Bruch­grenze zerreißt.

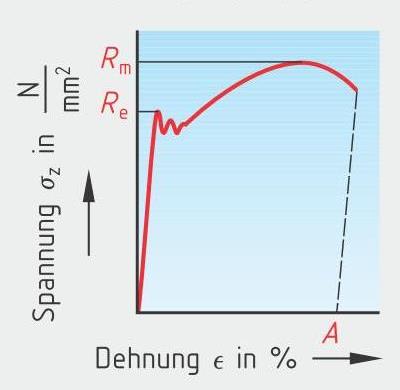
Abb. 1: Spannung-Dehnungsdiagramm „mit” ausgepägter Streckgrenze

In unserer Betrachtung beschränken wir uns haupt­sächlich auf den Propor­tionalitäts­bereich. Und wie nicht anders zu erwarten, gibt es eine propor­tionale Beziehung. Und zwar, dass die relative Längen­änderung propor­tional zur Zug­spannung ist. Wobei der Propor­tionalitäts­faktor vom Material abhängt:

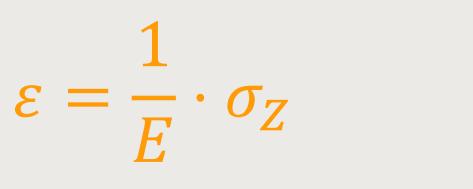
ε   ist die relative Längen­änderung in % (s.o.)
E   ist das Elastizitäts­modul des jeweiligen Werk­stoffs
(hier das Dehnungsmodul)
σ_z   ist die Zugspannung (Kraft pro Quer­schnitts­flächen­einheit)

Das bezeichnet man auch als das Hookesche Gesetz.

Je nach Material gibt es unter­schiedliche Dehnungs­moduln. Je größer dieser Modul wird, desto geringer wird die Längen­änderung bei einer bestimmten Zug­spannung. Die Einheit von diesem E-Modul ist:

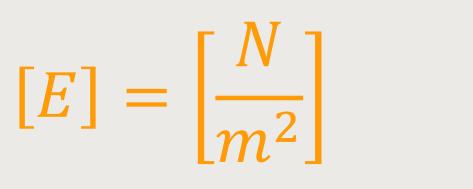
In Tabellen­büchern für den Maschinen­bau findet man eher die Einheit [N /mm²], mit entsprechend höherem Umrechnungs­faktor. Zum Beispiel beträgt der E-Modul bei Stahl 210.000 N/mm² und bei Aluminium 70.000 N/mm².

⇦ Kapitel Kapitel ⇨