Bei den „Schwingungen” geht es um Systeme, die perio­dische Ände­rungen ihres Zustandes durch­laufen. Das heißt, in regelmäßigen Abständen lassen sich gleiche Zustände beobachten. Es besteht aller­dings ein Unter­schied zwischen Schwingungen und Wellen. Eine Schwingung ist nur zeitlich periodisch, wogegen eine Welle zeitlich und räumlich periodisch ist. Eine Welle breitet sich im Allge­meinen in einem Medium aus, wobei es gibt auch solche gibt, die kein Medium dazu benö­tigen. Wir werden hier vor allem die mecha­nischen Aspekte in den Vorder­grund stellen.

Es geht vor allem darum, elastisch verform­bare Medien zu betrachten, in denen sich eine Welle räum­lich aus­breiten kann. So wie man es besonders anschau­lich von den Wellen an der Wasser­ober­fläche kennt. Die Bedeutung von Schwingungen und Wellen ist in der Physik sehr viel­fältig.

Neben den elastischen und mechan­ischen Wellen gibt es natür­lich auch die Licht­wellen und andere Wellen, die mit der Struktur der Materie im Zusammen­hang stehen. Nicht zu vergessen die atomaren Schwingungen und Wellen­aus­brei­tungen, wozu auch das quanten­physika­lische Wellen­bild gehört.

Wie man sieht, ist dieses Thema von großer Bedeutung. Daher ist der Forma­lismus, mit dem man Schwingungen und Wellen beschreiben kann, sehr wichtig. Und in gleich­artiger Weise lässt sich das auf sehr unter­schied­liche Systeme anwenden.

Wie kommt es zu „Schwingungen”? Wir erinnern uns, eine Schwingung ist eine regel­mäßige perio­dische Abfolge von verschie­denen Zuständen an einem Ort. Ein System wird solche Schwingungen durch­laufen, wenn ein Massen­punkt aus seiner Position aus­gelenkt wird und es anschlie­ßend eine rück­treibende Kraft gibt, die ihn wieder in diese Ausgangs­lage zurück­lenken möchte. Wobei diese rück­treibende Kraft propor­tional zur Aus­lenkung aus der Gleich­gewichts­lage ist. Eine der­artige Schwingung bezeichnet man auch als „harmonische Schwingung”. Man nennt so ein System auch einen „harmonischen Oszillator”.

In diesem Zusammen­hang könnte man sich ein relativ kleines Gewicht vor­stellen, das an einer Spiral­feder aufge­hängt ist. Die Spiral­feder wird dabei als ein elastisch verform­barer Körper ange­sehen. Zunächst schwingt nichts, weil sich alles in einer Gleich­gewichts­lage befindet. Wird nun das Gewicht um eine bestimmte Länge nach unten aus­gelenkt, dann wird proportional dazu eine rück­treibende Kraft entstehen. Lässt man das Gewicht wieder los, dann entsteht eine perio­dische Bewegung bzw. eine harmonische Schwingung. Würde es keine Reibungs­kräfte geben, bliebe diese Schwingung dauer­haft erhalten.

Wenn sich bei einem System eine harmonische Schwingung einstellt, nennt man dies, wie bereits erwähnt, einen „harmo­nischen Oszillator”. Wir werden einen solchen Oszillator der Einfach­heit halber, ähnlich wie bei einer Spiral­feder, 1-dimensional betrachten. Wie wird jetzt die Bewegungs­gleichung ausschauen? Da erinnern wir uns an das 2. Newton-Axiom:
Masse · Beschleunigung = wirkende Kraft

  ist die 2. Ableitung des Ortes (x-Koordinate) nach der Zeit

Die wirkende Kraft ist immer entgegen­gerichtet. Daher kann man die Schwingungs­gleichung schreiben als:

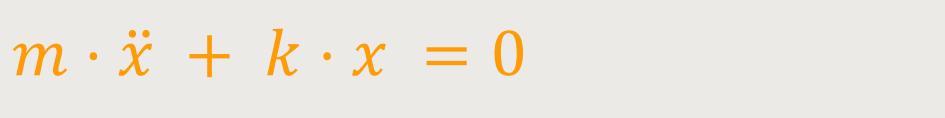
k   ist die Rückstell­konstante

Diese Rück­stell­konstante hängt davon ab, was für eine Feder man ver­wendet. Also, wie groß die Rück­stell­kraft bei einer bestimmten Aus­lenkung sein wird.

Wie lässt sich jetzt obige Gleichung mög­lichst einfach lösen? Dazu macht man zunächst einen Ansatz, der sich bei der­artigen Schwingungen und Wellen besonders bewährt hat, nämlich einen „komplexen Lösungs­ansatz”. Diese Vorgehens­weise lässt sich an der Form der Differential­gleichung erkennen. Wenn nur zweite Ablei­tungen und die Variable selbst vorkommen, hier ist es das x, bietet sich ein der­artiger Ansatz an. Und dieser Ansatz lautet:

a   ist ein konstanter Faktor

Hierbei ist es natür­lich wichtig, sich klar­zumachen, was für eine Größe man damit erhält. Es geht ja um die tatsäch­liche physika­lische Inter­pretation, zumal das Ganze ziemlich kompliziert aussieht. Bei der­artigen komplexen Ansätzen geht es immer darum, den Real­teil dieser komplexen Größe zu betrachten.

Man rechnet zwar komplex, benutzt aber den gesamten Forma­lismus, der in der komplexen Analysis ent­halten ist, und über­setzt dann das Ergebnis zurück in die reelle Situation, die experi­mentell vorliegt. Zum Schluss betrachtet man dann den Real­teil der entspre­chenden Größe.

In Verbindung mit der e-Potenz gibt es zum Beispiel die berühmte Eulersche Formel:

Der Realteil von e^iωt = cos ωt
Der Imaginärteil von e^iωt = i · sin ωt

Dann gibt es noch den Betrag dieser Potenz:

Das bedeutet, dass man hier eine Darstellung hat.

Bevor dieser Ausdruck in die Schwingungs­gleichung ein­gesetzt werden kann, benötigt man zunächst die zweite Ableitung:

a   ist die Konstante (hier die Amplitude)

Und wenn man sich oben das anschaut, ergibt sich:

Wenn man diese Ableitung in die Schwingungs­gleichung einsetzt, erhält man:

Schluss­endlich kann der ganze zeit­abhängige Teil ent­fallen, und auch auf die Amplitude kommt es nicht an. Daher bleibt nur noch ein ein­facher Zusammen­hang übrig:

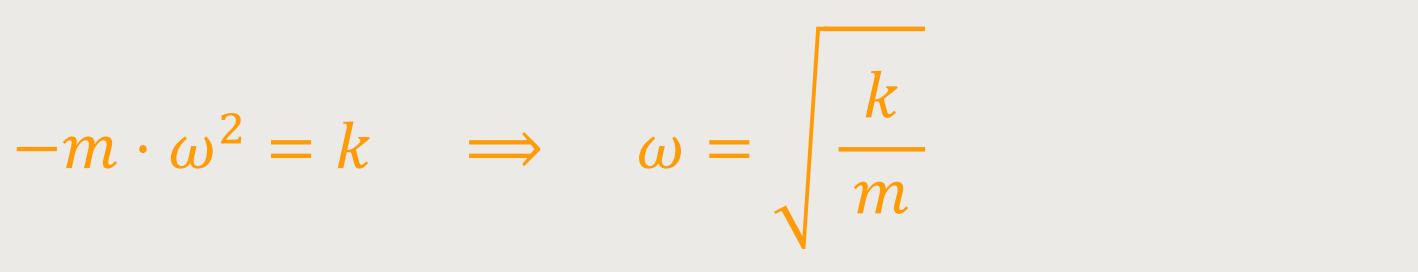
Damit erhält man eine wesent­liche Beziehung dafür, wie so eine Schwingung vor sich geht. Und jetzt muss man sich noch klar machen, was eigent­lich mit diesem ω (omega) gemeint ist.

Bisher haben wir die Schwingungs­gleichung betrachtet und einen komplexen Lösungs­ansatz gemacht. Dabei hat sich heraus­gestellt, dass das ω in einer ein­fachen Weise mit der Masse des schwingenden Teil­chens und mit der soge­nannten Rück­stell­konstante k zusammen­hängt. Die Rück­stell­konstante gibt den Propor­tionalitäts­faktor an, zwischen der Größe der Aus­lenkung aus der Gleich­gewichts­lage und der Größe der rück­treibenden Kraft.

Harmonische Schwingungen sind dadurch gekenn­zeichnet, dass die rück­treibende Kraft propor­tional zur Aus­lenkung aus der Gleich­gewichts­lage ist. In der Gleich­gewichts­lage ent­spricht die Aus­lenkung Null. Und es könnte natür­lich auch andere rück­treibende Kräfte geben, die dann aber zu unharmo­nischen Schwingungen führen würde.

Obige komplexe Darstellung hat den Sinn, dass wenn man letzten Endes zur konkreten Umsetzung für die realen Ver­gleiche mit experimen­tellen Vorgängen über­geht, dass man primär den Real­teil von dieser komplexen Lösung betrachtet. Und das ist etwas, was man sofort in ein­facher Weise mit Hilfe der soge­nannten Zeiger­darstellung klar­machen kann.

Die Größe x = a · e^iωt lässt sich in der komplexen Ebene in einem Koordinaten­kreuz dar­stellen. Die x-Achse entspricht der reellen Achse Re und die y-Achse der imaginären Achse Im. Um den Punkt 0,0 wird ein Kreis gezogen. Auf diesem Kreis bewegt sich die Größe x mit dem Radius a. Das e^iωt selbst bewegt sich auf einem Kreis mit dem Radius Eins, aber das a ist noch ein zusätz­licher Faktor und skaliert sozu­sagen seinen eigenen Kreis auf den Kreis mit Radius a auf.

Und wenn man sich zu einem gewissen Zeit­punkt auf dem Kreis befindet, ent­spricht der Winkel zwischen dem Radius a und der reellen Achse dem Wert ωt. Die Größe x kreist dann gegen den Uhrzeiger­sinn inner­halb der komplexen Ebene. Der Realteil ist dann immer lot­recht der Abschnitt auf der reellen Achse. Wobei der y-Wert dem Imaginär­teil entspricht.

Den Realteil von Re_x kann man grafisch aufge­tragen auf einer Achse, gegen die fort­schrei­tende Zeit t. Man erhält dann eine Schrauben­linie, die der Schwingung ent­spricht. In der Zeiger­darstellung rotiert quasi der Vektor-Zeiger in der komplexen Ebene gegen den Uhrzeiger­sinn, und der Real­teil dieser komplexen Zahl ist dann jeweils der Betrag, um den gerade die Aus­lenkung aus der Gleich­gewichts­lage erfolgt.

Da die Zeit fort­schreitet, kreist der Zeiger auf dem Kreis mit dem Radius a. Dieser Radius ist die größt­mögliche Aus­lenkung aus der Gleich­gewichts­lage. Daher nennt man diesen Radius a auch die „Amplitude”. Beides muss man jedoch von­einander unter­scheiden. Die Aus­lenkung ist die jeweilige Aus­lenkung zu einem gewissen Zeit­punkt. Dagegen ist die Amplitude die maximale Auslenkung.

⇦ Kapitel Kapitel ⇨