In der Praxis gibt es eine besonders wichtige Gleichung, die das Verhalten von Flüssig­keiten und Gasen unter gewissen Bedin­gungen beschreibt. Und zwar die sogenannte „Bernoulli-Gleichung”.

Um zu dieser Gleichung zu gelangen ist es erforder­lich, ein paar ideali­sierende, also einschrän­kende Voraus­setzungen zu machen. In der Realität ist es kaum möglich, für eine ganz beliebige Strömungs­form und ein ganz belie­biges Medium eine all­gemein gültige gesetz­mäßige Beziehung herzu­stellen. Meistens benötigt man dazu gewisse Voraus­setzungen, damit bestimmte Gesetz­mäßig­keiten erfüllt sind und man diese anwenden kann.

Im Fall der Bernoulli-Gleichung gibt es einige solcher Voraus­setz­ungen. Eine Voraus­setzung ist, das Fluid muss reibungs­frei sein. Außerdem setzt man voraus, dass das Fluid inkompres­sibel ist. Und als dritte Voraus­setzung, was die Strömungs­form betrifft ist, es soll sich um eine stationäre Strömung handeln.

Reibungsfrei bedeutet, dass es inner­halb des Fluids keine Reibung zwischen den verschie­denen aneinander abglei­tenden Flüssig­keits­schichten gibt. Es wird also keinen Energieübertrag von mecha­nischer Energie in thermische Energie geben. Denn bei Reibungs­vorgängen entsteht ja immer thermische Energie, und das ist etwas, was dem Energie­erhaltungs­satz entgegen­wirkt. Das heißt, wenn man Reibungs­kräfte im System berück­sichtigen muss, dann sind die wirkenden Kräfte nicht konservativ, und dann gilt der mecha­nische Energie­erhaltungs­satz nicht mehr.

Jetzt setzen wir jedoch die Reibungs­freiheit voraus, um den mecha­nischen Energie­erhaltungs­satz zu gewähr­leisten. Aller­dings kann man sich gerade in der Hydro­dynamik keines­wegs nur auf reibungs­freie Fluide beschränken. Doch dazu mehr in einem anderen Kapitel. Diese Gesamt­energie­erhaltung hat für die weitere Betrach­tung einen großen Vorteil, insbe­sondere wenn es um das Verhalten der einzelnen Fluid­elemente in einer Strömung geht.

Des Weiteren setzen wir voraus, dass die Strömung inkompres­sibel ist bzw. sich das Fluid nicht nennens­wert kompri­mieren lässt. Das kann auch bei gas­förmigen Fluiden der Fall sein, wenn man keine zu großen Geschwindig­keiten zulässt. Wenn also eine Inkompres­sibilität gegeben ist, dann werden die einzelnen Volumen­elemente, die sich durch das Fluid hindurch­bewegen, immer ein konstantes Volumen haben.

Wir bezeichnen auch hier wieder dieses Volumen mit dV. Und aus der Stationari­tät folgt, dass die einzelnen Fluid­elemente sich längs der Strom­linien bewegen. Wie wir schon gesehen haben, fällt der Begriff der Strom­linie mit dem Begriff der Bahn­kurve eines Fluid­elements bei stationären Strömungen zusammen.

Wenn es insbe­sondere um die Erhaltung der mecha­nischen Gesamt­energie geht, kommt es darauf an, wie groß die kine­tische Energie eines Fluid­elements mit dem konstanten Volumen dV sein wird. Und es stellt sich auch die Frage, wie groß wird die poten­tielle Energie sein, wenn man die Strömung im Feld der Gravi­tation auf der Erd­ober­fläche betrachtet? Und letzt­lich muss man sich fragen, wenn es unter­schied­liche Drücke in diesem System gibt, wie groß wird denn die Arbeits­zuführung aufgrund des Druckes sein? In der Praxis kommen für solche Anwen­dungen Pumpen zum Einsatz, die nichts anderes machen, als Druck­differenzen zu erzeugen. Also ohne Anfangs­druck keine Druck­differenz.

Wir betrachten jetzt gedank­lich einen Ausschnitt einer Strömung, mit einer gewissen Quer­schnitts­fläche A. Nun soll die Strömung ein Stück ds weiter­fließen. Dann ergibt sich daraus ein Volumen V. Aus Richtung der Strömung herrscht ein Druck p. Man kann sich leicht über­legen, was für eine Arbeit zugeführt werden muss, wenn die Strömung um dieses Stück ds weiter­läuft. Die Kraft auf die Quer­schnitts­fläche ist ja nichts anderes als p · A (Kraft = Druck · Fläche). Und diese Kraft wird multi­pliziert mit der zurück­gelegten Strecke ds der Strömung. Die Arbeits­zuführung in diesem System lautet somit:

Damit sieht man auch, was der Druck für eine zusätz­liche wichtige Bedeutung in der Thermo­dynamik hat.

In unserem Fall können wir jetzt von der Erhaltung der mecha­nischen Gesamt­energie ausgehen, weil keine innere Reibung in dem System wirkt. Wir haben ja voraus­gesetzt, dass das Fluid als weitest­gehend reibungs­frei ange­sehen werden kann. Nun lässt sich die Energie­erhaltung beschreiben, indem man einfach sagt:
Die Arbeits­zuführung plus der kine­tischen Energie plus der poten­tiellen Energie entspricht:

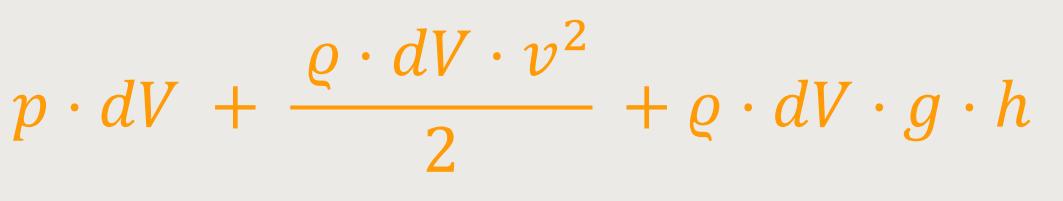
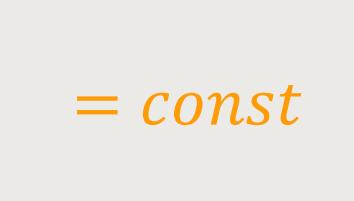
Und das muss letzten Endes konstant bleiben, denn was man an Arbeit zuführt, plus die entspre­chenden Energien muss insgesamt wegen der Energie­erhaltung eine „Konstante” bleiben.

Und wegen der Inkompres­sibilität wird sich das Volumen dV im Zuge der ganzen Strömung nicht ändern. Insofern lässt sich dieses dV aus der Beziehung wegkürzen. Damit ergibt sich:

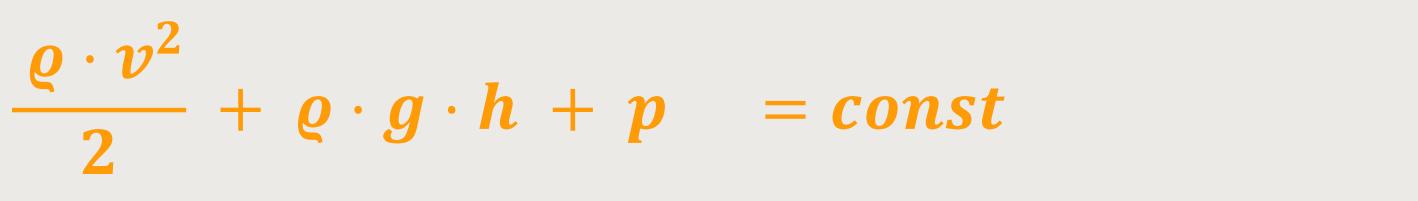
Das ist die berühmte Bernoulli-Gleichung.

Also, es geht um die kine­tische Energie pro Volumen­einheit, sowie die poten­tielle Energie pro Volumen­einheit und die Arbeits­zuführung pro Volumen­einheit, sprich dem Druck. Diese drei Energien müssen insgesamt wegen der Erhaltung der mecha­nischen Gesamt­energie konstant bleiben. Wie gesagt, die Gleichung gilt nur für den Fall einer Strömung eines reibungs­freien Fluids bei konstanter Dichte und Stationarität.

In vielen anderen Anwendungs­fällen wird aller­dings die Bedingung der Reibungs­freiheit nicht annähernd gegeben sein. Dann funk­tioniert diese Gleichung nicht mehr. In derartigen Fällen gibt sie sinnlose und falsche Ergeb­nisse. Wie wir gleich noch sehen werden, ergibt sich daraus eine Paradoxie.

Diese Gleichung scheint sich nicht immer mit dem zu decken, was unser anschau­liches Verstän­dnis ist. Denn in den meisten Fällen gehen wir davon aus, dass bei einer Flüssig­keits­strömung auch Reibung mit im Spiel ist. Gerade wenn man mittels einer Pumpe, ein vermeint­lich zähes Wasser durch eine Leitung pressen will. Da geht es doch primär darum, Reibung zu überwinden.

Es gibt aller­dings Systeme, insbe­sondere gas­förmige Systeme, wo diese Reibung wirk­lich sehr gering ist und damit vernach­lässigbar. Dort lässt sich diese Bernoulli-Gleichung gut anwenden.

Was ist aber, wenn die poten­tielle Energie keine wichtige Rolle spielt. Das ist dann der Fall, wenn eine Strömung im Gravitations­feld waage­recht erfolgt oder wenn es gar kein Gravitations­feld gibt. In diesem Fall haben wir nur noch den Term:

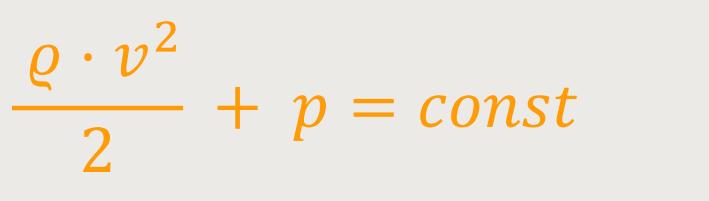
Das bedeutet, wenn bei konstanter Dichte die Geschwindig­keit immer größer wird, umso kleiner muss der Druck werden, damit die Summe der beiden konstant bleibt. Herrschen große Geschwindig­keiten, gibt es demnach kleine Drücke. Das klingt im ersten Moment etwas paradox.

Eigen­tlich sollte man meinen, je größer die Geschwindig­keit ist, desto größer müssen auch die Drücke sein. Dieses Empfinden hat man deshalb, weil man die Strömung oftmals mit Reibung in Verbindung bringt. Man denkt oftmals, wenn ich Druck ausübe, muss ich auch Reibung über­winden. Wir haben in unserem Beispiel aber keine Reibung und dadurch ergibt sich diese merkwürdige Situation.

Diese Folgerung nennt man daher auch das „Hydro­dynamische Paradoxon”. Paradoxon im Sinne von über­raschend, weil man nicht damit rechnet. Die Gase sind besonders für ihre Reibungs­freiheit bekannt, und komprimieren lassen sie sich besonders gut. Letzteres wird aller­dings erst ab Schall­geschwindig­keit der Fall sein.

Wie lässt sich die Bernoulli-Gleichung veranschaulichen?

Wenn zum Beispiel ein Luft­strahl aus einer Düse austritt, dann hat die Luft in den Strom­linien unter­schied­liche Geschwindig­keiten. An den Rand­bereichen werden die Geschwindig­keiten immer kleiner, während in der Mitte die höchsten Geschwindig­keiten vorhanden sind. Jetzt stellen wir die Düse senk­recht und platzieren im Luft­strom etwas außer­halb des Zentrums einen leichten Tisch­tennisball.

Aufgrund der unterschied­lichen Geschwindig­keiten des Gases und der sich damit verän­dernden Druck­verhält­nisse wird der Ball stabil im Zentrum tänzeln. Eine größere Geschwindig­keit bedeutet ein kleinerer Druck. Deshalb wird der Ball immer wieder ins Zentrum herein­gezogen. Und damit ist gerade die Stellung im Zentrum die stabilste.

Man kann die Bernoulli-Gleichung auch dazu verwenden, um die Umströmung von Körpern zu beschreiben. Natür­lich alles nur unter der Voraus­setzung der Reibungs­freiheit. Und das ist zugegebener Maßen schon eine sehr einschrän­kende Voraus­setzung. Dennoch lassen sich für allge­meinere Anwendungs­fälle gewisse Aspekte ableiten.

Nehmen wir an, wir haben einen Körper, der nur aus einer Richtung mit einem Gas umströmt wird. Die Strom­linien werden dann entspre­chend an dem Körper tangential vorbei laufen. Das sind dann die Tangential­linien an die Geschwindig­keits­vektoren . In ausrei­chender Ent­fernung vom Körper gibt es in einem Punkt B eine Anfangs­geschwindig­keit v_₀. Außer­dem soll an diesem Punkt ein Druck p_₀ herrschen. Man kann dieses System jetzt aus zwei Blick­winkeln betrachten.

Einerseits wäre es möglich, dass der umströmte Körper in Ruhe ist, und man bläst auf diesen. Anderer­seits, und das ist der allge­meinere Fall, ist das Medium in Ruhe und der Körper bewegt sich durch das Gas. So wie das beim Auto, dem Zug oder einem Flugzeug der Fall ist. Man kann sich gut vor­stellen, dass in ausrei­chender Entfer­nung, also an einem Punkt, weit weg von diesem Hinder­nis, einfach nur der ungestörte Atmos­phären­druck herrscht. Und erst bei Heran­nahmen dieses umströmten Körpers wird es zu Verände­rungen kommen.

Der andere wichtige Punkt, den wir betrachten, ist der Stau­punkt S. Im Stau­punkt, der unmittel­bar vor dem Hinder­nis liegt, wird die Geschwindig­keit v = 0, weil die Strömung zur Ruhe kommt. Und der Druck im Stau­punkt wird p sein. Die beiden Größen v_₀, p_₀ beziehen sich auf das ungestörte statische Medium. Während die Größen v = 0 und p die Situation direkt beim umströmten Hindernis betreffen.

Und wenn man das Ganze jetzt auf einer Höhen­linie betrachtet, so dass der Term ϱ · g · h aus der Bernoulli-Gleichung immer der gleiche bleibt, dann kann man den Term mit in die Konstante hinein­ziehen und es bleibt dann nur stehen:

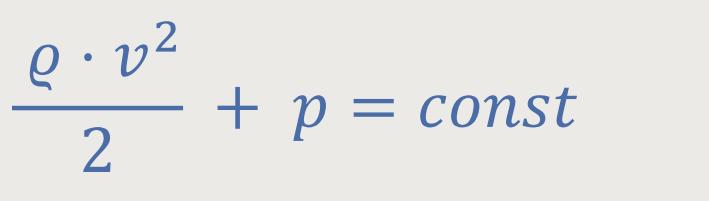
Was für eine Konstante das ist, ist gar nicht so wichtig, so lange sich der Strömungs­bereich konstant verhält. Dann müssen nur die Bedin­gungen beim Beobachtungs­punkt B und beim Stau­punkt S betrachtet werden, und die Summe der Energie muss die gleiche bleiben. Laut Bernulli erhalten wir dann:

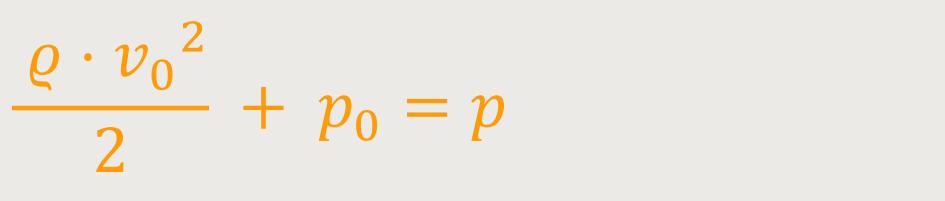
p   ist der Druck im Stau­punkt
p_₀   ist der statische Atmos­phären­druck

Auf diese Art und Weise erhält man durch Umformung sehr schnell eine einfache Folgerung:

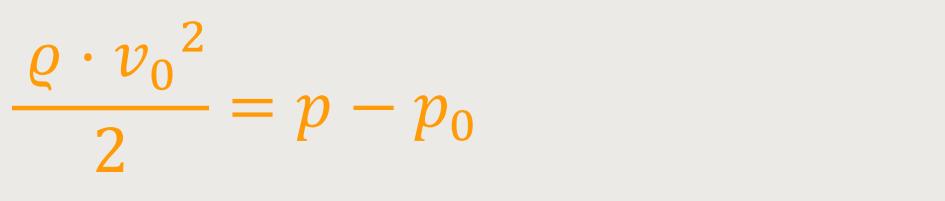
Das ist jetzt die Druck­differenz, auf die es in Wirk­lich­keit ankommt.

Die Differenz zwischen dem Druck im Stau­punkt und dem allge­meinen Druck nennt man in der Hydro­dynamik allge­mein den „Stau­druck”. Der Stau­druck p - p_₀ ist gerade dieses Δp und wird normaler Weise wesent­lich kleiner sein, als der normale atmos­phärische Druck. Es sei denn, man liegt hier annähernd bei Schall­geschwindig­keit. Dann kommt es zu sehr hohen Druck­differenzen, und das Fluid ist nicht mehr inkompres­sibel. In einem solchen Fall bewegen wir uns aber außer­halb des Geltungs­bereichs der Gleichung.

Daraus kann man jetzt durch Umformen sehr einfach eine Methode gewinnen, um die Geschwindig­keit zu ermitteln:

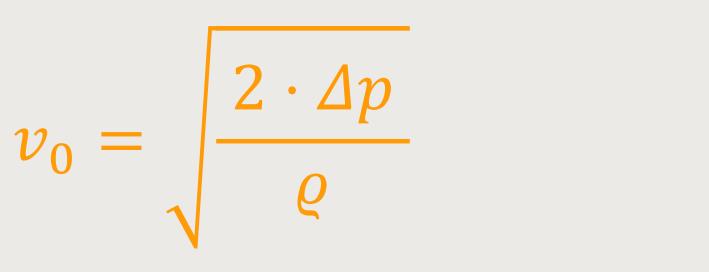
Damit erhält man eine gute Möglich­keit, die Geschwindig­keit der Strömung relativ zu dem ange­strömten Hindernis zu bestimmen. In der Praxis wird die Bestimmung der Strömungs­geschwindig­keit mit Hilfe des soge­nannten „Prandtl-Rohres” durch­geführt.

Das Prandtl-Rohr verkörpert ein ange­strömtes Hindernis. Es hat vorne am Stau­punkt ein Loch und seit­lich umlaufend weitere Löcher. Das vordere Loch hat eine Verbindung zu einer mittig im Rohrkörper heraus­tretenden Druck­röhre. Und die seit­lichen Löcher haben ihrer­seits eine Verbindung zu einer zweiten mittig heraus­tretenden Druck­röhre. Man kann dann zwischen diesen unter­schiedlich angeordneten Löchern die Druck­differenz p - p_₀ messen.

Bei gemessener Druck­differenz und bekannter Gasdichte, beispiels­weise bei Luft = 1,29 kg /m³, erhält man so die Geschwindig­keit v_₀. Man kann damit recht genau die Strömungs­geschwindig­keit in einem strömenden Medium bestimmen. Mittler­weile gibt es die unter­schied­lichsten Ausfüh­rungen eines solchen Prandtl-Rohres.

Jetzt wollen wir einen anderen Aspekt der Strömung heraus­greifen, und zwar den Aspekt der Wirbel­bildung und der Zirkulation.

Wir setzten auch hier wieder reibungs­freie Fluide voraus. Wie lässt sich aber charakte­risieren, ob eine Strömung wirbel­haft ist oder nicht? Dazu führen wir den Begriff der „Zirkulation” ein, den wir nach­folgend an zwei Beispielen illus­trieren werden.

Wenn wir Nach­folgend von Wirbeln sprechen, dann zeich­nen sie sich dadurch aus, dass die Geschwindig­keits­vektoren in einer Strömung rund­herum laufen. Aller­dings werden die Vektoren zum Zentrum hin immer kleiner. Um das näher beschrei­ben zu können, ist es günstig, geschlossene Bahn­kurven zu betrachten. Also keine Spiral­kurve, die zur Mitte hin immer enger wird, sondern man zeichnet in die Wirbelströmung zahl­reiche konzen­trische Kreise ein.

Bei einer Wirbel­strömung betrachtet man sinn­voller Weise eine kreis­förmige Kurve, während es bei einer gerade verlaufenden Strömung ohne Wirbel­bildung ein recht­eckiger Kurven­verlauf sein wird. Jetzt betrachtet man längs einer solchen geschlossenen Kurve ein Linien­integral · d . Diese Größe ist zunächst natür­lich keine Arbeit. Denn wir haben ja keine Kraft skalar multi­pliziert mit einem Weg­element, sondern eine Geschwindig­keit skalar multi­pliziert mit einem Wegelement.

Hierzu definieren wir uns die Zirku­lation längs einer geschlos­senen Kurve. Wobei diese geschlos­sene Kurve immer aufge­fasst werden kann als die Rand­kurve einer Fläche. Es ergibt sich daraus für die Zirkulation:

  ist der Geschwindigkeitsvektor
d   ist das Wegstück

Die geschlossene Fläche ent­spricht dem Flächen­inhalt der jeweils betrach­teten Kreis­fläche oder dem Recht­eck. Wenn man entlang dieser Rand­kurve die jeweilige Fläche umschreitet, dann erkennt man, dass die Geschwindig­keits­vektoren und die Wegs­tücke d alle gleich orientiert sind, und die Summe über · d ergibt eine Größe Z ≠ 0.

Bei einem rechteckig verlau­fenden Linien­integral laufen die Vektoren linear in eine Richtung herum. In diesem Fall wird es so sein, dass einige Weg­stücke d auch sen­krecht zu den Geschwindig­keits­vektoren liegen werden. Außer­dem heben sich die Werte auf den entgegen gesetzten Seiten wieder auf. Daraus ergibt sich die Größe Z = 0. Somit liegt in einer gerade verlau­fenden Strömung keine Zirku­lation vor und damit auch keine Wirbel­bildung.

Das ist eine weitere wichtige Anwen­dung des Linien­integrals neben der Arbeit und außer­dem eine weitere wichtige Anwendung des Skalar­produktes (siehe Definition des Arbeits­begriffes). Nun kann man diese Zirku­lation mathe­matisch relativ leicht umformen.

Im vorherigen Kapitel haben wir schon in Verbin­dung mit den Strom­flüssen gesehen, wie nütz­lich es ist, ein Flächen­integral mithilfe des Gauß'schen Integral­satzes in ein Volumen­integral umzuformen.

Jetzt geht es aber um eine leicht veränderte Form, nämlich von einem Linien­integral in ein Flächen­integral umzuformen. Diese Umformung geschieht mithilfe des Stokes'schen-Integralsatzes:

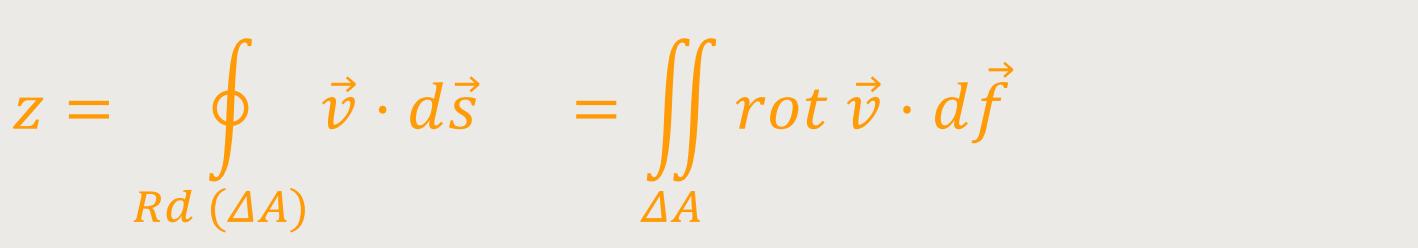
Der Gauß'sche Satz hat uns den Divergenz-Operator gebracht. Hier beim Stokes'schen Satz tritt die Rotation eines Vektor­feldes auf. Und die Zirku­lation hängt mit der Rotation des Vektor­feldes zusammen. Wenn man das nur über ein kleines Flächen­element betrachtet, sodass sich diese Rotation nicht mehr nennens­wert über dieses Flächen­element ändert, kann man auch schreiben:

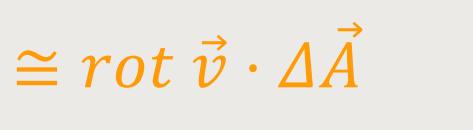
Wenn rot || Δ (parallel) ist, lässt sich das auch als Betrag schreiben:

Z / ΔA   ist die Wirbel­dichte

Und damit erhält man etwas Analoges, was bereits auf die Diver­genz zutraf. Dort wurde die Diver­genz als Quell­dichte bezeichnet. Und zwar, wenn man ein kleines Volumen betrachtet, und beobachtet, was aus diesem Volumen heraus­fließt, dann ist dieser Fluss durch den Rand des Volumens pro Volumen­einheit die Divergenz.

Hier hat man jetzt eine Dimension weniger. Man betrachtet eine Fläche mit ihrem Rand. Und wenn nun längs dieses Randes in dieser Flüssig­keit eine gewisse Zirku­lation vorhanden ist, dann muss man diese Zirku­lation pro Flächen­einheit bestimmen, also durch die Fläche dividieren, um den Betrag des Rotations­vektors zu erhalten. Die Rotation ist daher in entspre­chender Weise eine Wirbel­dichte.

Hier ist es die Zirku­lation rund um eine Fläche pro Flächen­einheit. Bei der Quell­dichte war es der Fluss aus einem Volumen heraus pro Volumen­einheit. Man kann also gut erkennen, wie die Rotation des Vektor­feldes mit der Zirku­lation und der Wirbel­bildung zusammen­hängt. Man kann sich jetzt auch leicht vorstellen, wie das ausschaut.

Wenn man eine Wirbel­strömung betrachtet, dann laufen an den geschlos­senen Strom­linien die Geschwindig­keits­vektoren rund herum. Daraus ergibt sich dann eine Fläche, die quasi umlaufen wird. Jetzt denkt man sich noch eine zweite parallele Fläche. Und dann gibt es noch die Rotations­vektoren , die parallel zu ΔA, also senk­recht auf die Flächen in Fluss­richtung das Feld durch­laufen. Genau genommen sind das die Vektoren rot , die in die Richtung der Wirbel­achse des Wirbels zeigen.

Das Vektor­feld selbst beschreibt einen Wirbel, während die Rotations­vektoren in der Achse dieses Wirbels liegen. Die Strom­linien sind dann die Tangential­vektoren an die Geschwindig­keits­vektoren. Und die Wirbel­linien sind Tangential­linien an den Rotations­vektor. Dadurch lässt sich eine Gesetz­mäßig­keit für reibungs­freie Fluide aufzeigen:

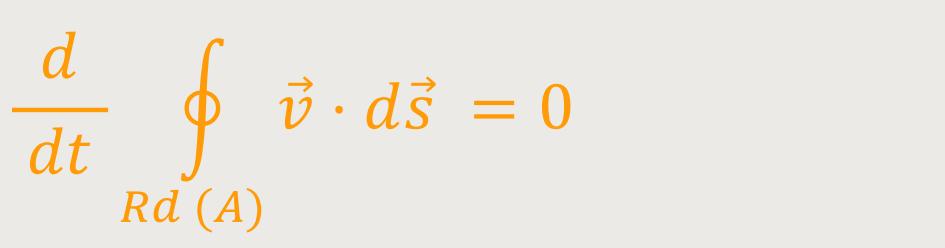
Das ist der soge­nannte Thomsonsche Wirbel­satz.
Die zeit­liche Ableitung obiger Zirku­lation ist gleich Null. Das bedeutet, dass die Zirku­lation in reibungs­freien Fluiden erhalten bleibt.

Wenn dagegen eine nennens­werte Reibung herrscht, dann wird aufgrund dieser Reibung diese Zirku­lation zurück­gehen.

Zum Beispiel bleibt ein Rauch­wirbel (Toruswirbel) erhalten und würde sich ohne Luft­reibung immer weiter fort­setzen.

⇦ Kapitel Kapitel ⇨