Den „Auftrieb” in Fluiden kann man sehr gut mithilfe des Archime­dischen Prinzips beschreiben. Hierzu betrachtet man der Einfach­heit halber eine Flüssig­keit. Zunächst ist diese Flüssig­keit in einem Behälter im Gleich­gewicht. Sie verhält sich ruhig unter dem Einfluss der Schwer­kraft. Unter­sucht man mitten im Behälter ein kleines Flüssig­keits­volumen, dann ruht dieses im Gleich­gewicht in der gesamten Flüssig­keit. Das Gewicht, das dieses Volumen an Flüssig­keit hat, wird von den umgebenden Flüssig­keits­ober­flächen kompensiert. Wäre das nicht so, würde dieses Flüssig­keits­volumen hinabsinken.

Nun geht man einen Schritt weiter, und nimmt gedank­lich dieses kleine Flüssig­keits­volumen weg und ersetzt es durch einen anderen Körper. Die Drücke der verblei­benden Flüssig­keit auf dieses ausge­tauschte Volumen werden in Summe wieder die gleiche Auftriebs­kraft liefern, wie vorher. Jetzt kommt es darauf an, welches Gewicht das ausge­tauschte Volumen hat.

Wenn der Körper ein größeres Gewicht hat, wird er unter­gehen. Wenn er ein gerin­geres Gewicht hat, wird er auf­steigen. Wenn er dagegen das gleiche Gewicht hat, also das gleiche Volumen und die gleiche Dichte, dann schwebt er dort. Deswegen legen die Taucher auch Blei­gewichte an, um möglichst schwebend durch das Wasser zu gleiten.

Das heißt also, dass die Auftriebs­kraft, die auf einen Körper in einem Fluid wirkt, nichts anderes ist als das Gewicht der verdrängten Fluidmenge.

Auftrieb = Gewicht des verdrängten Fluids

Wobei Gewicht sehr wohl von Masse zu unter­scheiden ist. Gewicht ist eine Kraft. Die Kraft, mit der eine Masse im Gravitations­feld der Erde zu Boden gezogen wird. Bei der Auftriebs­kraft liefern die Eis­berge ein schönes Anschauungs­objekt. Wasser hat ja die Eigen­schaft, dass seine Dichte geringer wird wenn es friert. Insofern sinkt das Eis nicht hinab.

Eine weitere Eigen­schaft von Fluiden, und insbe­sondere von Flüssig­keiten ist die Ober­flächen­spannung.

Was kann man sich unter einer „Ober­flächen­spannung” vorstellen?

Es gibt soge­nannte „Kohäsions­kräfte” zwischen den Molekülen. So ein Molekül hat zu allen seinen benach­barten Molekülen anzie­hende Wechsel­wirkungs­kräfte, die sich dann im Gleich­gewicht alle zu Null kompen­sieren. Daher verharrt das Molekül an der Stelle, wo es sich gerade befindet. Man spricht auch von der „Kohäsion”, welche die Flüssig­keit zusammenhält.

Ein Molekül an der Flüssig­keits­ober­fläche hat dagegen nur in eine Richtung Wechsel­wirkungs­kräfte. In diesem Fall gibt es eine resul­tierende Kraft, die nach innen zeigt. Das ist eine Kraft, die sich aufgrund der Kohäsion zwischen den Flüssig­keits­molekülen ergibt. Das sind letzt­lich elektro­magne­tische Kräfte, die dazu führen, dass es Wechsel­wirkungen zwischen den Molekülen gibt.

Was passiert aber, wenn sich diese Flüssig­keits­ober­fläche vergrößert. Bei einer größeren Ober­fläche müssen ein paar Moleküle aus dem Innen­bereich heraus­treten, um an die Ober­fläche zu gelangen. Und um das zu ermöglichen, muss eine Arbeit verrichtet werden. Und zwar eine Arbeit gegen die nach innen gerichtete Kohäsions­kraft. Diese Arbeit ist charakte­ristisch für die jeweilige Flüssig­keit. Wenn man also ein Gefäß um eine gewisse Fläche ΔA und damit die Ober­fläche erweitert, muss ein gewisser Arbeits­aufwand ΔW verrichtet werden.

Je Größer die Fläche ΔA ist, desto mehr Moleküle müssen an die Ober­fläche treten. Und desto größer wird die verrichte Arbeit ΔW. Wie man sieht, verhält sich der Zusammen­hang proportional. Und der Propor­tionalitäts­faktor ist die Ober­flächen­spannung σ:

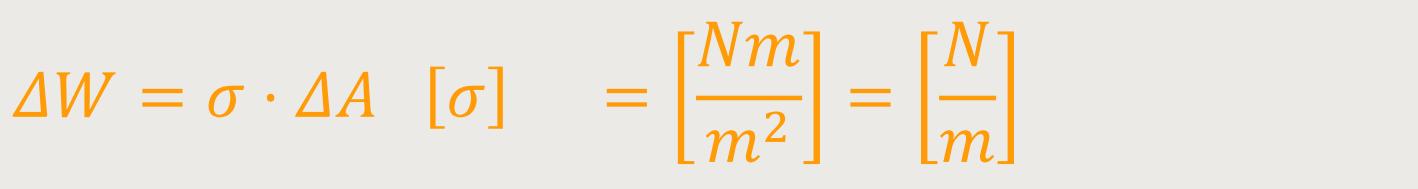
Die Ober­flächen­spannung ist üblicher­weise nicht sehr groß, sondern man bewegt sich da in Größen­ordnungen von [mN /m] (Milli-Newton pro m). Wasser spielt hierbei wieder eine besondere Rolle. Es hat im Verhältnis eine besonders große Ober­flächen­spannung. Hier liegt man bei etwa 70 mN /m. Während Alkohol nur 20...30 mN /m hat. Sehr wichtig ist die Ober­flächen­spannung bei Pflanzen, insbesondere bei den Bäumen.

Die Einheit N /m schaut ja mehr nach einer Kraft / Länge aus. Was versteht man darunter und wie könnte man das veranschau­lichen?

Im Nachfolgenden betrachten wir dazu eine Art Seifen­blase, also eine dünne Flüssig­keits­schicht.

Eine Flüssigkeits­lamelle möchte aufgrund der inneren Spannung so klein wie möglich bleiben. Denn je kleiner sie ist bzw. je kleiner ihrer Ober­fläche wird, desto weniger Ober­flächen­moleküle müssen vorhanden sein. Obwohl diese Lamelle sehr dünn ist, hat sie eine Ober­seite und eine Unter­seite. Im Verhältnis zum Volumen entspricht das einer sehr großen Ober­fläche.

Wird nun eine solche Lamelle an einem Rahmen aufge­spannt und eine in der Ebene quer laufende Strebe einseitig gezogen, kann die Ober­fläche nicht anders, als sich auszu­weiten. Das bedeutet zwangs­läufig, dass die Ober­fläche größer wird und mehr Moleküle aus dem Innern heraus­treten müssen. Es wird somit Arbeit geleistet. Die Person, die an der Quer­strebe zieht, verrichtet diese Arbeit. Die verrichtete Arbeit ist dann Kraft · über­strichene Weg­strecke in der gleichen Richtung. Die aufge­wendete Arbeit stellt sich wie folgt dar:

F   ist die aufgewendete Kraft
Δs   ist der Weg, den die Stange über­streicht

Bei der Kraft handelt es sich um diejenige Kraft, die man gerade braucht um die Spannung, die diese Lamelle aufbaut, zu kompen­sieren.

Anderer­seits kann man auch die Vergrö­ßerung der Ober­fläche betrachten, die dabei entsteht. Die Ober­fläche der Lamelle wird mit ΔA bezeichnet. Da es bei der Lamelle eine Ober­seite und eine Unter­seite gibt, bedeutet das:

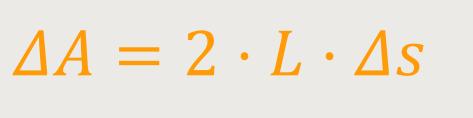
L   ist die Breite des aufge­spannten Rahmens

Jetzt lässt die Arbeit ΔW aufgrund der Definition der Ober­flächen­spannung alter­nativ ausrechnen:

Man greift mit der Quer­strebe längs einer Grenz­linie dieser Flüssig­keits­oberfläche an. Daraus ergeben sich eine vordere und eine hintere Grenz­linie. Also, die gesamte Länge, an der hier ange­griffen wird, ist genau genommen 2 · L.

Wenn man nun beide Forma­lismen mit­einander vergleicht, dann ist das letzten Endes dieselbe Arbeit. Dementspre­chend kann man sofort die benötigte Kraft ausrechnen:

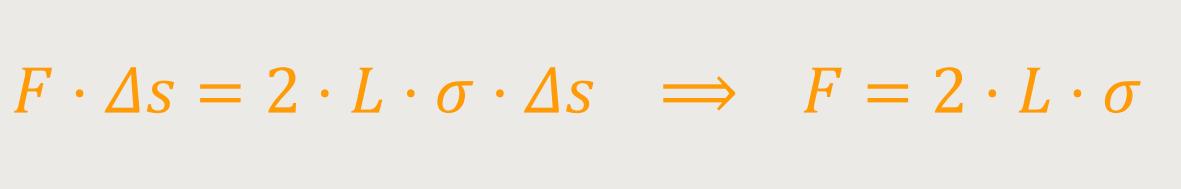
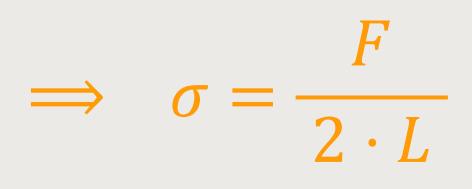
Daraus ergibt sich, dass die Ober­flächen­spannung konkret als Kraft pro Länge der Grenz­linie einer Ober­fläche aufgefasst werden kann. Und das entspricht dann diesem N /m. Es geht daher um die Frage, wie viel Newton muss aufgewendet werden, um eine gewisse Länge der Ober­fläche auseinander zu ziehen.

Jetzt kann man diese Ober­flächen­spannung auch dazu verwenden, um zu erklären, warum Flüssig­keiten in engen Röhren und engen Kanälen aufsteigen. Das ist eine der ganz wichtigen Eigen­schaften der Ober­flächen­spannung.

Unter dem Begriff „Kapillare” versteht man eine enge Röhre, die nur ein paar zehntel Millimeter Durch­messer hat. In solch dünnen Röhren neigen Flüssig­keiten dazu, aufzu­steigen. Man sagt auch, die Flüssig­keit steigt aufgrund der „Kapillari­tät” auf. Und diese Kapillari­tät hat mit der Ober­flächen­spannung einer Flüssig­keit zu tun.

Denken wir uns wieder ein Gefäß, in das ein dünnes Glas­röhrchen bis knapp unter die Wasser­ober­fläche ein­taucht. Also, ein Röhr­chen mit einer engen Kapillare. Was wir jetzt gedank­lich durch­spielen wollen, führt in das recht komplizierte Gebiet der Ober­flächen­physik. Man geht davon aus, dass die betrach­teten Ober­flächen von der jewei­ligen Flüssig­keit „benetzt” werden. Das heißt, wenn man die Ober­fläche eintaucht, und wieder rausholt, bleibt ein dünner Flüssig­keits­film an der Ober­fläche haften, selbst wenn es nur mono­molekular ist. Die Flüssig­keits­moleküle bleiben aufgrund von Ober­flächen­kräften, auch Van der Waals Wechsel­wirkungs­kräfte genannt, haften. Diese Wechsel­wirkungs­kräfte sind letzt­lich wieder elektro­dynamische Kräfte.

Es gibt aber auch nicht benetz­bare Systeme. Bei Teflon zum Beispiel perlt das Wasser ab. Alles in allem gibt es benetz­bare und nicht benetz­bare sowie mehr oder weniger benetz­bare Ober­flächen. Wie benetz­bar eine Ober­fläche ist, wird durch das Phänomen des Kontakt­winkels beschrieben. Der Kontakt­winkel Null bedeutet, dass sich ein Flüssig­keits­tropfen ganz flach aus­breitet, wenn man ihn auf eine Ober­fläche auf­trägt. Dagegen spricht man von einem größeren Kontakt­winkel, wenn sich die Flüssig­keit zu einem Tropfen ausbildet. Queck­silber bildet sich sogar zu einem kugel­förmigen Tropfen aus, der sich nicht benetzen will.

Letzt­lich sind das Fragen der Energie­zustände. Man spricht dann von „Grenz­flächen­energie” zwischen der Flüssig­keit und dem darunter­liegenden Substrat. Es handelt sich quasi um substanz­abhängige Eigen­schaften. Aber selbst wenn man nur Wasser hernimmt, und es auf dem Blatt einer Lotus­pflanze betrachtet, ist der Kontakt­winkel ca. 170° und es perlt ab. In der Regel liegt man natür­lich weit darunter, weil die meisten Ober­flächen recht gut benetzbar sind.

Bei unserer Betrachtung setzen wir eine voll­ständige Benetz­barkeit voraus. In diesem Fall ist es so, dass die Kapillare durch Ein­tauchen schon einmal mit der Flüssig­keit benetzt wurde. Die Innen­fläche dieser Kapillare trägt bereits eine dünne, viel­leicht nur mono­molekulare Schicht der Flüssig­keit. Die Flüssig­keit will aber seine Ober­fläche so klein wie möglich halten, damit nicht zu viele Ober­flächen­moleküle vorhanden sind.

Die Moleküle streben somit nach innen, wo ihr Energie­zustand geringer ist. Und das bedeutet wiederum, dass sich in der Kapillare am Rand eine seit­liche Erhöhung des Wasser- oder Flüssig­keits­spiegels ergibt. Dadurch wird die verblei­bende Ober­fläche ober­halb des Flüssig­keits­spiegels geringer. Je weiter das Wasser nach oben steigt, desto güns­tiger wird es dann. Aber warum steigt es oftmals nicht endlos nach oben?

In diesem Fall bedarf es einer Arbeit gegen die Schwer­kraft, um so hoch aufsteigen zu können. Und es steigt gerade so hoch, dass es ein optimales Verhältnis gibt. Dann spricht man von der Steig­höhe h, um die eine Flüssig­keit auf­steigt. Und diese Steig­höhe lässt sich eben­falls mithilfe der Ober­flächen­spannung ausrechnen:

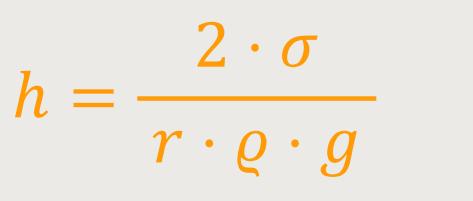
σ   ist die Oberflächen­spannung
g   ist die Fall­beschleu­nigung
ϱ   ist die Dichte der Flüssig­keit
r   ist der Radius der Kapillare

Je dichter die Flüssig­keit ist, desto mehr Hub­arbeit muss verrichtet werden. Der Radius steht im Nenner, und je dünner die Kapillare im Innern wird, desto höher steigt die Flüssig­keit.

Also, für voll­ständige Benetz­barkeit gibt es obigen ein­fachen Zusammen­hang. Und so lässt sich mittels der Steig­höhe bei bekanntem Kapillar­radius die Ober­flächen­spannung ermitteln. Flüssig­keiten mit einer höheren Ober­flächen­spannung σ steigen dementspre­chend auch höher auf. Und was noch wichtiger ist, dieses Phänomen ist dafür verant­wortlich, dass in den Bäumen, wo es viele kleine Kapillare gibt, die Flüssig­keit vom Boden aufsteigt.

⇦ Kapitel Kapitel ⇨