Man kann davon ausgehen, dass in einer Strömung die Masse eines strö­menden Fluids nicht verloren geht, sondern es muss eine Erhal­tung geben. Und diese „Massen­erhaltung” bei den Strö­mungen werden wir jetzt mög­lichst klar formal dar­stellen. In der gleichen Weise lässt sich der Forma­lismus auch verwenden, um in der Elektro­dynamik die „Ladungs­erhaltung” darzustellen. Also, wie bereits erwähnt, gibt es ein breites Anwendungs­feld.

Um die Massen­erhaltung verständ­lich zu machen, muss zunächst erklärt werden, was man unter den Begriffen „Fluss” und „Quellen” versteht.

Man kann davon ausgehen, dass mit einer Flüssig­keits­strömung oder Gas­strömung etwas trans­portiert wird. Wir trans­portieren in diesem Fall ein Volumen eines Fluids oder anders ausge­drückt eine Masse. Auf diese Weise kann man ermitteln, welches Volumen dieses Fluids pro Zeit­einheit durch eine bestimmte Quer­schnitts­fläche A in der jewei­ligen Strömung hindurch treten wird. Das nennt man dann den „Volumenfluss”. Und das ist wiederum nichts anderes als ein Flächen­integral:

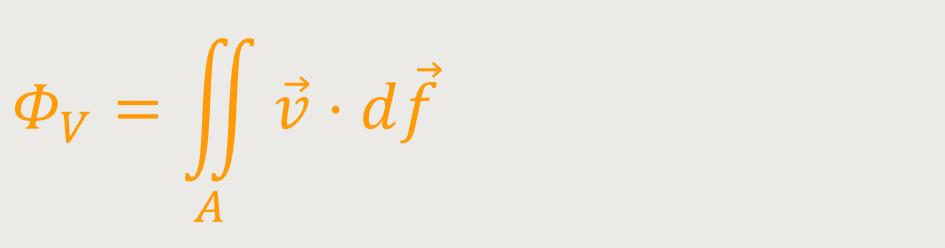
Φ_V   ist der Volumen­fluss
d   ist der Flächen­vektor

Hierzu kann man sich eine quadra­tische Querschnitts­fläche A in dem jeweils betrach­teten Volumen­strom denken. Recht­winklig dazu werden an den vier Ecken die Geschwindig­keits­vektoren einge­zeichnet. Daraus ergibt sich ein Quader. Und das Volumen dieses Quaders ist gerade das Volumen an Flüssig­keit, welches durch die Quer­schnitts­fläche in der Zeit­einheit hin­durch getreten ist. Die Geschwindig­keit ist in diesem Fall der Weg, der pro Zeit­einheit zurück­gelegt wird. Daher wird durch die Quer­schnitts­fläche A ein gewisses Volumen hindurch treten.

Im Allge­meinen wird die Geschwindig­keit in der Flüssig­keit nicht immer gleich groß sein. Daher führt man in solchen Fällen immer eine Integra­tion durch. Man unter­teilt die Recht­eck­fläche in viele kleine Teil­flächen, und man hat dann lauter Flächen­elemente d f, und bildet daraus ein Produkt mit der Geschwindig­keit multi­pliziert mit d f.

Jetzt sieht man aber in obiger Formel das Skalar­produkt · d stehen, und die Idee dabei ist, dass es natür­lich darauf ankommt, ob diese Flüssig­keits­strömung senk­recht auf der Quer­schnitts­fläche steht oder ob sie unter einem gewissen Winkel wirkt. Denn wenn die Quer­schnitts­fläche unter einem schrägen Winkel zur Strömung steht, wird natür­lich auch das Flüssig­keits­volumen, welches jetzt durch eine geneigte Fläche hindurch tritt abwei­chend sein. Und um das mög­lichst über­sichtlich und klar dar­stellen zu können, betrach­tet man für jedes Teil­flächen­element einen Flächen­vektor d .

Der Flächen­vektor ist ein Vektor, der stets senk­recht auf das ihm zuge­ordnete Flächen­element steht. Und die Länge bzw. der Betrag dieses Flächen­vektors ist dann gleich dem Flächen­inhalt dieses Flächen­elements. Wenn somit diese Strömung senk­recht zur Fläche strömt, dann ist es so, dass der Flächen­vektor und der Geschwindig­keits­vektor parallel zueinander ange­ordnet sind. In diesem Fall ist das Skalar­produkt der beiden einfach gleich dem Produkt der Beträge. Daher ist das Volumen, welches pro Zeit­einheit durch­tritt, ein­fach Fläche · Geschwindigkeit.

Wenn die Flächen­elemente in der Betrach­tung aber schräg stehen, also unter einem Winkel, dann steht auch der Flächen­vektor d schräg. Und das muss natür­lich berück­sichtigt werden. Man bildet dann nach wie vor das Skalar­produkt, aber jetzt geht der Cosinus des Neigungs­winkels in die Berechnung mit ein. Der Volumen­fluss der Flüssig­keit wird deshalb wegen der schräg­gestellten Quer­schnitts­fläche geringer sein.

Und wenn diese Fläche gar tangen­tial liegen sollte, sodass die Strömungs-Geschwindig­keits­vektoren in der Fläche sind, dann wird der Flächen­vektor senk­recht zur Geschwindig­keit stehen. In diesem Fall wird dieses Skalar­produkt gleich Null sein. Also, durch die Betrachtung des Skalar­produktes von · d trägt man dem Umstand Rechnung, dass man im Allge­meinen auch Quer­schnitts­flächen zulassen möchte, die irgend­wie schräg zur Strömungs­geschwindig­keit liegen. Wenn man aber nur Quer­schnitte betrachtet, die einfach senk­recht zur Strömung liegen, wird der Flächen­vektor und der Geschwindig­keits­vektor immer parallel zueinander sein, und dann hat man ledig­lich das Produkt der Beträge.

Obiger Forma­lismus ist so definiert, dass die jeweils betrach­tete Fläche, über die integriert wird, also die gesamte Quer­schnitts­fläche, beliebig liegen kann, um das Volumen zu ermitteln, welches pro Zeit­einheit durch­tritt. Das ist natür­lich eine integrale Größe, und man betrachtet eine bestimmte Fläche in dieser Strömung. Deshalb ist es wichtig, wenn man so einen Volumen­fluss betrachtet, immer dazu zu sagen, was ist das für eine Fläche? Sprich, steht diese Fläche ggf. unter einem gewissen Winkel?

In der Hydro­dynamik interessiert uns im Zusammen­hang mit der Massen­erhaltung auch der Massen­fluss.

Ähn­lich wie beim Volumen geht es darum, die „Masse” des Fluids pro Zeit­einheit auszu­rechnen. Das ist relativ leicht durch­zuführen, weil das Volumen und die Masse über die Dichte zusammen­hängen:

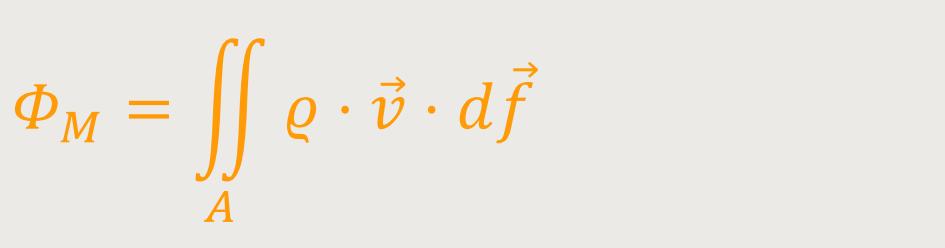
Masse = Dichte · Volumen

ϱ   ist die Dichte
· d   ist das Volumen pro Zeiteinheit

Wenn man das Volumen, wie oben bereits behandelt, mit der Dichte der Flüssig­keit multi­pliziert, dann bekommt man als Ergebnis die Masse, die pro Zeit­einheit durch das entspre­chende Flächen­element hindurch tritt. Und die Summation über alle diese Quer­schnitts­flächen führt dann auf die gesamte Masse, die pro Zeit­einheit die Fläche A durch­strömt. Und dieses ϱ · nennt man deshalb auch die „Fluid-Stromdichte”:

Die Fluid-Strom­dichte gibt im Wesent­lichen den Massen­fluss pro Flächen­einheit an. Wenn man das anschlie­ßend über die Quer­schnitts­fläche d integriert, lässt sich der gesamte Massen­fluss darstellen. Genau­genommen ist das der Massen­fluss pro senk­rechte Quer­schnitts­flächen­einheit.

Mit den zuvor genannten Begriffen können wir jetzt die Massen­erhaltung näher beschreiben. Um das entspre­chend darstellen zu können, betrachten wir ein bestimmtes makros­kopisches Volumen V in der Strömung. Wenn man die Dichte der Flüssig­keit oder des Gases kennt, lässt sich die gesamte Masse des Fluids im Inneren dieses bestimmten Volumens V berechnen:

dV   ist ein Volumenelement

Das heißt, dieses Volumen V denkt man sich wieder aufge­teilt in viele kleine Würfel, die dieses ganze Volumen bilden. Und wenn dieses Fluid, hier viel­leicht ein Gas, an verschie­denen Stellen unter­schied­liche Dichten hat, dann muss an jeder Stelle die dort gültige Dichte zugrunde gelegt werden. Anschließend bildet man ein Produkt aus ϱ · dV, und summiert dann alle ϱ · dV auf. Schließ­lich geht man zu immer feineren Eintei­lungen über und erhält dann wie üblich obiges Volumen­integral. Man verwendet hier drei Integrations­zeichen, um klarzu­machen, dass es sich um einen 3-dimensio­nalen Integrations­bereich handelt.

Wenn die Dichte konstant ist, also nicht abhängig vom Ort, lässt sich das auch einfacher schreiben:

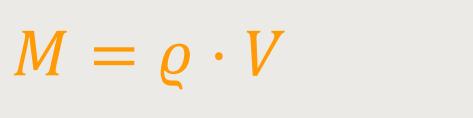
Aber wir wollen uns nicht nur auf spezielle Fälle beschränken, sondern auch zulassen, dass das Dichte­feld eine Dichte sein kann, die orts­abhängig ist. Damit erhalten wir die Möglich­keit, bei unter­schiedlichen Dichte­verhält­nissen zu einem bestimmten Zeit­punkt, die gesamte Masse des Fluids inner­halb dieses Volumens darzu­stellen.

Jetzt betrachten wir die Masse, die pro Zeit­einheit aus diesem Volumen heraus­fließt. Wie können wir uns das ausrechnen?

Hier legen wir zunächst obigen Begriff „Massen­fluss” zugrunde. Das entspricht ja der Masse des Fluids, welche pro Zeit­einheit durch eine Fläche A hindurch strömt. In diesem Fall ist es aber nicht die Quer­schnitts­fläche, sondern die Rand­fläche bzw. Mantel­fläche. Denn wir betrachten ja einen Behälter, bei dem das Volumen nur durch die Mantel­fläche heraus­fließen kann.

Deswegen bildet man ein Flächen­intergral, wo man als Fläche den geschlossenen Rand bzw. die geschlossene Mantel­fläche dieses Volumens V zugrunde legt. Geschlossen bedeutet, dass diese Fläche ihrer­seits keine Rand­kurve hat. So wie eine Kugel, die auch keine Rand­kurve hat. Also, eine allgemein geformte geschlossene Fläche, die ein ebenso geformtes Volumen einschließt:

Somit ergibt sich ein entspre­chendes Flächen­integral:

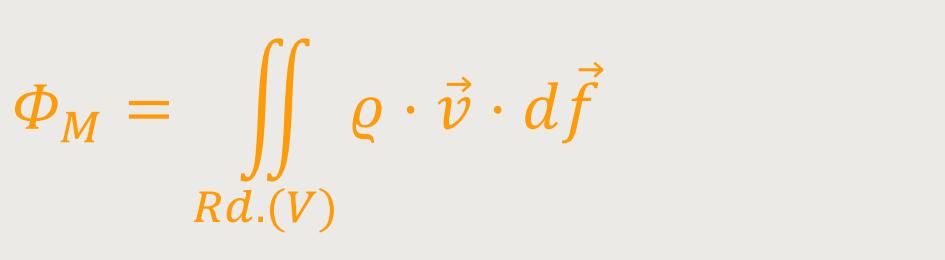
Wir integrieren über den Rand Rd des Volumens V.

Und da gibt es jetzt die Möglich­keit, ein derartiges Flächen­integral über einen Rand eines räum­lichen Bereiches mit Hilfe des berühmten Gauß'schen Integral­satzes umzuformen. Das ist im Wesent­lichen nur eine mathe­matische Umformung. Man stellt dieses Flächen­integral, über den Rand eines Volumens, einfach nur dar als ein Volumen­integral des ganzen Volumens über die Divergenz:

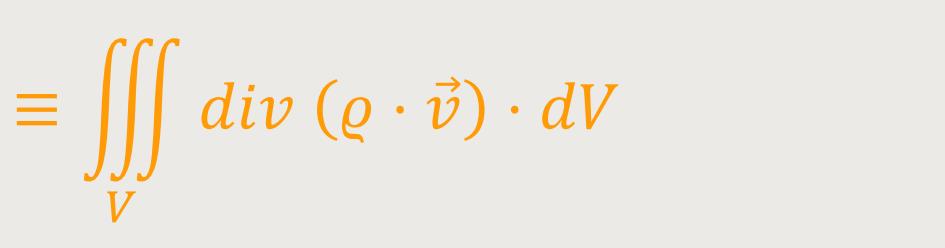
dV   ist wieder ein Volumen­element

Das ist eine identische Umformung, nur halt eben mithilfe des Gauß'schen Integral­satzes. Die Divergenz eines Vektor­feldes lässt sich in Kompo­nenten darstellen:

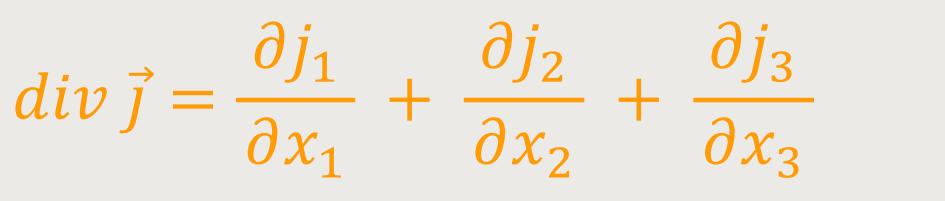
= ϱ ·   ist die Fluid-Stromdichte (Massenflussdichte)

Wir betrachten hier die Masse, die pro Zeit­einheit aus dem Volumen heraus­fließt, umgeformt mithilfe des Gauß'schen Integral­satzes. Was lässt sich daraus schluss­folgern?

Einer­seits wird die Gesamt­masse des Fluids darge­stellt als ein Volumen­integral. Anderer­seits stellt sich die Masse, die pro Zeit­einheit aus dem Volumen heraus­tritt ebenfalls als Volumen­integral dar. Wie spielt jetzt die Massen­erhaltung mit hinein? Und da trägt die Physik wieder eine wichtige Rolle.

Was muss man sinn­voller Weise voraus­setzen, damit es zu einer Massen­erhaltung kommt? Zunächst einmal, wenn etwas aus einem Volumen heraus­fließt, dann ist nachher zwangs­läufig weniger drin. Also, eine gewisse Masse verlässt pro Zeit­einheit dieses Volumen. Dann muss in gleichem Maße die Masse im Inneren dieses Volumens zurück­gehen. Das ist die Idee hinter der Massen­erhaltung. Dementspre­chend muss gelten:

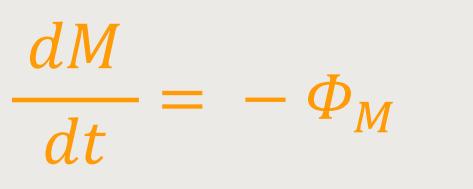
dM /dt   ist die zeit­liche Änderung der Gesamt­masse

Wenn dM /dt kleiner als Null ist, dann war der Fluss aus dem Volumen heraus positiv, deshalb das Minus auf der rechten Seite. Eine Abnahme der Gesamt­masse geht einher mit einem positiv nach außen gerichteten Fluss. Und daher kann man sofort erkennen, was passiert, wenn man entspre­chend einsetzt:

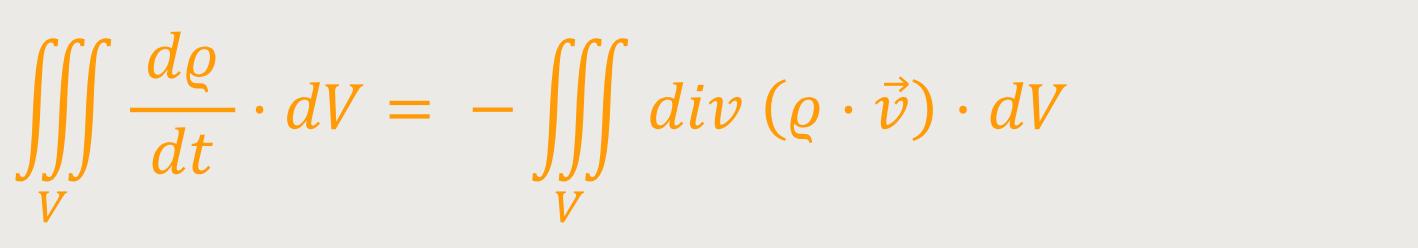
Diese Beziehung ist richtig, wenn sie für beliebige Volumina gilt, also wenn sie für die Integranden dϱ /dt und −div (ϱ · ) zutreffend sind. Und so kann man hier unmittel­bar von einer integralen Beziehung auf eine differen­tielle Beziehung über­gehen. Das heißt, es ist jeden­falls erfüllt, wenn folgendes gilt:

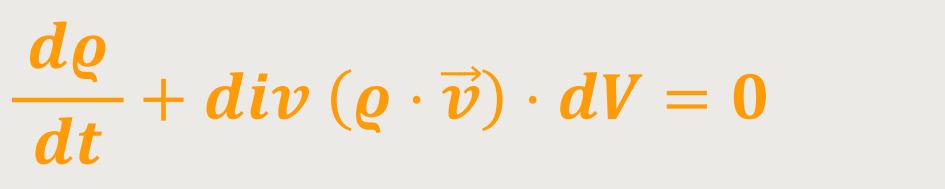
Diese Gleichung ist eine ganz wichtige Differential­gleichung.
Das ist die sogenannte Kontinuitäts­gleichung und sie sagt aus: „Die Masse in dem System ist erhalten.”

ϱ ·   ist die Fluid-Stromdichte

In der Elektro­dynamik ist es dann die „elek­trische” Strom­dichte.

Wenn es sich um inkompres­sible Fluide handelt, kann man sofort erkennen, dass sich die Dichte nicht ändert. Daraus ergibt sich:

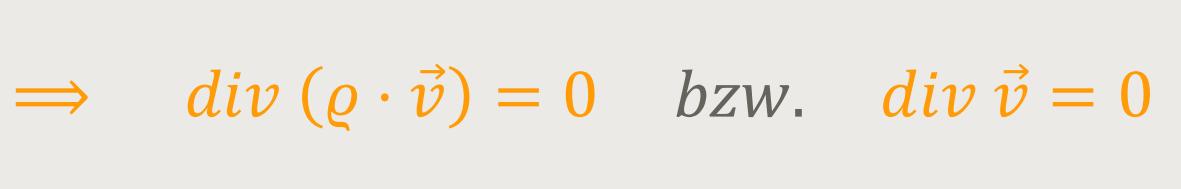
Man kann es einem Strömungs­feld, also einem Feld von Strömungs-Geschwindig­keits­vektoren, sofort ansehen, ob es sich um eine inkompres­sible Strömung handelt. Man benötigt dazu nur die Diver­genz von . Wenn diese gleich Null ist, dann handelt es sich um ein inkompres­sibles Fluid. Anson­sten wird die Diver­genz ≠ Null sein, und dann ergeben sich auch zeit­liche Ände­rungen der Fluid­dichte.

⇦ Kapitel Kapitel ⇨