Wie lässt sich die „Zähigkeit” eines Fluids charakte­risieren? Es wurde schon mehr­fach ange­deutet, dass Zähig­keit etwas mit der inneren Reibung zu tun hat. Bisher wurde die innere Reibung bei Fluiden vernach­lässigt. In der Praxis ist dieser Ein­fluss aber von sehr großer Bedeu­tung. Und in Anbetracht dessen wird man auf völlig neue Gesetz­mäßig­keiten stoßen. Diese innere Reibung hängt mit einem Impuls­transport inner­halb einer Flüssig­keit zusammen.

Nehmen wir an, wir haben zwei horizontal über­einander ange­ordnete Platten mit einem definierten Abstand. Dazwischen gibt es ein Fluid, welches den Bereich zwischen den beiden Platten ausfüllt. Es kann sich dabei um eine Flüssig­keit oder ein Gas handeln. Die untere Platte ist in Ruhe, die obere Platte soll sich seit­wärts mit einer gewissen Geschwindig­keit _₀ bewegen. Zu Beginn ist die Geschwindig­keit der oberen Platte Null. Der Abstand der beiden Platten h wird mit der z-Achse definiert.

Wenn das Fluid ganz reibungs­frei ist, wird es keine Auswirkung auf die obere Platte haben, dass sich ein Fluid dazwischen befindet, weil die Platte an der Flüssig­keit abgleitet. Die Flüssigkeit wird in diesem Fall keine Reibung ausüben.

Wenn es aber innere Reibung gibt, dann werden die einzelnen Flüssig­keits­schichten aneinander abgleiten und dabei wird Reibung entstehen. Außerdem, und das zeigt die Erfahrung, wird ein solches Fluid auch an den Grenz­flächen haften. Das heißt, das Fluid wird an der oberen Platte mit einer Geschwindig­keit _₀ mitge­zogen, wogegen es an der unteren Platte ruht. Es bildet sich zwischen den Platten ein lineares Geschwin­digkeits­profil mit unter­schied­lichen Geschwindig­keits­vektoren aus. Wie lässt sich diese Reibung in der Flüssig­keit charakte­risieren?

Der entschei­dende Punkt ist, dass an der oberen Platte mit einer gewissen Kraft parallel zur unteren gezogen werden muss, damit die obere Platte sich mit der konstanten Geschwindig­keit _₀ bewegt. Und je größer diese Kraft ist, die man benötigt, desto größer ist die Zähig­keit des Fluids. Bei Öl zum Beispiel muss man mehr an der Platte ziehen, als bei Wasser; und bei Wasser mehr, als bei Luft.

Diese Kraft wird zunächst einmal propor­tional zur Fläche der beiden Platten sein. Dann kommt es auch darauf an, wie stark die einzelnen Flüssigkeits­schichten aneinander abgleiten. Es geht also um den Geschwindig­keits­gradienten mit der z-Achse dv /dz. Wie schnell sich also der Betrag der Geschwindig­keit mit der der z-Achse ändert. Bei einer linearen Ände­rung könnte man dafür auch schreiben v_₀ /h.

Aber im Allge­meinen lässt sich eine lineare Ände­rung nicht immer voraus­setzen. Beide Ausdrücke sind dennoch je nach Betrachtungs­fall angebracht.

Und je näher die Platten bei gleicher Geschwindig­keit zusammen rücken, desto stärker wird der Gradient werden, und desto stärker muss man an der oberen Platte ziehen. Zusätz­lich kommt es noch darauf an, um was für ein Fluid es sich dabei handelt. Das wird durch den Parameter der Zähigkeit η beschrieben. Und so kommt man auf die Definition:

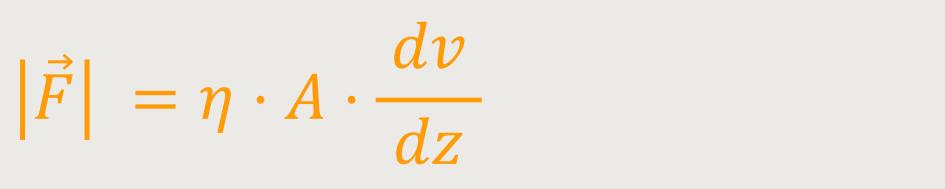
η   ist die Visko­sität oder die Zähig­keit
||   ist der Betrag der Reibungs­kraft
A   ist die Gesamt­fläche der Platten

Auf diese Weise kann die Zähigkeit oder Visko­sität eines Mediums gemessen werden.

Man könnte sich noch fragen, ob die Zähig­keit vom Material der Platte abhängt? In den aller­meisten Fällen ist es so, dass zähe Flüssig­keiten grund­sätzlich an der Ober­fläche eines Randes komplett haften bleiben, unab­hängig davon was für ein Material man wählt. Dement­sprechend spielt die chemische Zusammen­setzung der Platten keine große Rolle.

Nachfolgend sind einige Zähig­keits­werte in η [mPa · s] (Millipascal) angegeben:

Glyzerin	1480
Wasser	1,002
Benzol	0,65
Luft	0,017
Wasserstoff	0,0086

Ein weiterer wesent­licher Faktor ist die Temperatur­abhängig­keit. Denn die Werte gelten immer nur für eine bestimmte Temperatur. Mit zuneh­mender Temperatur nimmt die Flüssig­keits­zähigkeit ab, weil sich die Moleküle leichter in Bewegung setzen.

Bei Gasen ist es genau umgekehrt. Die Zähig­keit eines Gases nimmt mit höherer Temperatur zu, weil durch die stärkere Bewegung auch ein stärkerer Impuls­transport zwischen den Molekülen stattfindet.

Eine weitere Zähig­keit ist die „kinematische Zähigkeit”. Diese bezeichnet man als ν (nu), und das ist nichts anderes als:

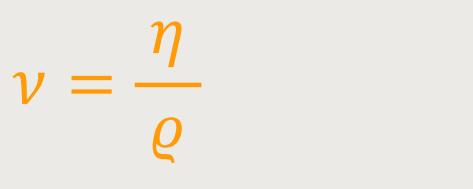
Darauf werden wir weiter unten in Verbin­dung mit der Renolds-Zahl zu sprechen kommen.

Mit Hilfe der Zähigkeit kann man bei einfachen Geometrien die Wider­stands­kräfte bzw. die Durch­sätze ausrechnen. Im Nach­folgenden werden wir einige solcher ein­fachen Geometrien betrachten. Im ersten Fall geht es um die laminare Strömung durch ein zylin­drisches Rohr.

Wenn eine zähe Flüssig­keit durch ein Rohr tritt, dann haftet diese am Rand, und es bildet sich ein parabo­lisches Geschwindig­keits­profil aus, wobei in der Mitte die höchste Geschwindig­keit ist und zum Rand hin die Geschwindig­keiten immer geringer werden. Aufgrund dieses para­bolischen Geschwindig­keits­profils lässt sich der Volumen­durchsatz Q ausrechnen. Also wie viel Flüssigkeit pro Zeit­einheit hindurch­tritt:

Q   ist das Volumen des Fluids pro Zeit­einheit
R   ist der Radius des Rohres
Δp   ist der Differenz­druck am Eingang/Ausgang des zylindr. Rohres

Dieses Gesetz geht auf Hagen-Poisseulle zurück.

Je größer der Differenz­druck wird, umso mehr steigt der Volumen­durchsatz und zwar propor­tional dazu. Und je größer die Zähig­keit des Fluids ist, desto geringer wird der Volumen­durchsatz sein. Um einen größeren Durch­satz zu erreichen, und damit auch eine größere Geschwindig­keit durch dieses Rohr, benötigt man dazu einen größeren Differenz­druck. Oder, je größer der Durch­messer, desto größer der Durch­satz.

Eine andere wichtige Anwendung zäher Fluide ist die Umströ­mung einer Kugel. Bei der Umströ­mung einer Kugel hat man ein relativ kompli­ziertes Strömungs­profil.

Für laminare Strömungen gilt in Näherung:

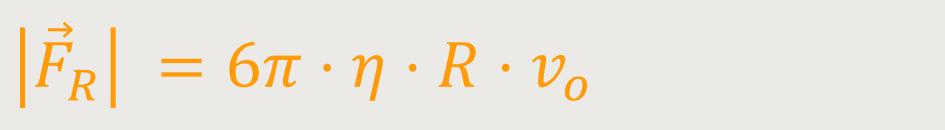
Das ist das soge­nannte Stokes'sche Gesetz.

|_R|   ist der Betrag der Reibungskraft
R   ist der Kugelradius
v_₀   ist die Geschwindig­keit der Kugel relativ zum Fluid

Oft sind die Strömungs­vorgänge so kompliziert, dass es gar nicht so einfach ist, sie wirklich konkret zu berechnen. Wir betrachten hier nur einfache Spezial­fälle für offen­sichtliche Geometrien. Möchte man dagegen kompli­zierte Geometrien betrachten wie zum Beispiel Autos und Schiffe, dann verwendet man oft Wind­kanäle oder Strömungs­kanäle. Dort lässt sich die Umströmung von kompli­zierten Hinder­nissen experi­mentell und empirisch ermitteln.

Wegen der Größe der Modelle müssen aller­dings gewisse Skalen­faktoren einführt werden. Doch von kleinen Modellen auf die Wirklich­keit zu schließen, ist oft sehr proble­matisch. Die Werte sind im Allge­meinen nicht über­tragbar. Und um das entspre­chend unter­suchen zu können ist es wichtig, dass man sich dabei auf die wesent­lichen Dimen­sionen konzen­triert.

Zunächst verein­facht man alles in Form einer Linear­dimension l. Das kann sogar ein Radius oder ein Durch­messer sein. Dann gibt es noch die Anström­geschwindig­keit v. Und natür­lich gehört auch die kine­matische Zähig­keit ν = η /ϱ dazu.

Aus diesen Größen lässt sich eine ein­fache dimensions­lose Konstante gestalten. Und wenn der Betrag dieser Konstante sowohl bei dem Original als auch bei dem Modell im Strömungs­kanal die gleichen Werte hat, kann man davon ausgehen, dass man ähn­liche Verhäl­tnisse hat. Diese dimensionslose Konstante nennt man auch die Reynolds-Zahl R_e.

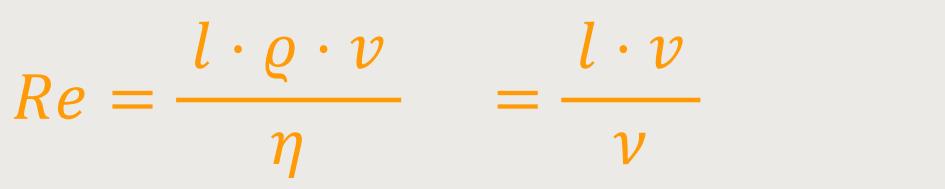
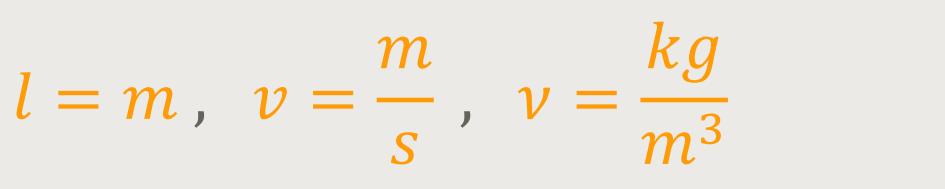
Die Reynolds-Zahl beschreibt nicht nur die Ähnlich­keit von Strömungen bei Modell­experimenten, sondern sie hat auch eine andere Funktion. Man kann sie ansehen als das Verhält­nis zwischen Trägheits­kräften und Reibungs­kräften. Denn die Massen­dichte ϱ hat etwas mit der Träg­heit des Fluids zu tun.

Je mehr Masse vorhanden ist, desto träger ist das Fluid. Außer­dem, je größer die Geschwindig­keit, desto mehr wird die Träg­heit dazu führen, dass sich die Strömungs­linien nicht mehr am Körper anlegen. Es wird sich womöglich eine turbu­lente Strömung ausbilden. Somit lässt sich die Reynolds-Zahl ansehen, als das Verhältnis zwischen:

Nehmen die Träg­heits­kräfte über­hand, dann wird es turbu­lent. Sind dagegen die Reibungs­kräfte vorherr­schend, dann bleibt die Strömung laminar. Das zeigt sich auch in der Realität. Es gilt annähernd:

Man kann also durch Ausrechnen der Reynolds-Zahl leicht heraus­finden, ob die Strömung laminar oder turbulent sein wird. Es gibt aller­dings eine Besonder­heit beim zylin­drischen Rohr. Dort macht die Träg­heit gar nicht so viel aus, weil die Bewegung nur gerad­linig ist. Bei einem zylin­drischen Rohr kann man bis zu einer Reynolds-Zahl R_e= 2300 gehen, bevor das Fluid in Turbulenz umschlägt.

Es gibt eine Reihe von tech­nischen und empi­rischen Tricks, wie man Strömungen opti­mieren kann. Auch Mikro­strukturen an Ober­flächen führen dazu, dass Flüssig­keiten besser an Ober­flächen abgleiten. Das hat sich mittler­weile zu einer eigenen Wissen­schaft etabliert, die sich mit diesen Strukturen auseinander­setzt. Man nennt sie die „Bionik”. Durch unter­schiedliche Gestaltung im Mikro- und Nano­bereich kann man die Strömungen von zähen Medien wesent­lich beeinflussen.

Es gibt in der „Hydro­dynamik” und „Aero­dynamik” eine Viel­zahl unter­schied­licher dimensions­loser Zahlen. Und man ist bemüht, die gesamte Hydro­dynamik möglichst in dimensions­loser Form darzu­stellen. Dazu nimmt man nur solche Größen, die bereits von sich aus gar keine Dimension haben. Damit lassen sich allgemein­gültigere Gleichungen aufstellen. Das ist eine bewährte Vorgehens­weise, um all­gemeine Strömungs­formen in über­sicht­licher Form darstellen zu können. Solche dimensions­losen Zahlen sind immer Verhältnis­zahlen zwischen unter­schied­licher Terminologie.

⇦ Kapitel Kapitel ⇨