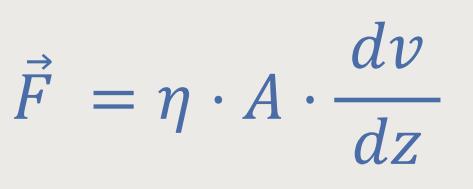Bisher haben wir immer über Gleich­gewichts­zustände gesprochen. Jetzt wollen wir diese Gleich­gewichts­zustände verlassen, und eine räum­liche Inhomo­genität der entspre­chenden Systeme in Betracht ziehen.

Wenn es um Nicht­gleich­gewichts­zustände geht, spricht man insbe­sondere von drei Vor­gängen. Das sind einmal der Impulstransport, der Massetransport und der Energietransport (Wärmemenge).

Beim „Impuls­transport” geht es um einen Vorgang, den wir bereits in der Hydro­dynamik schon besprochen haben. Der Impuls­transport führt näm­lich zu einer Wechsel­wirkung zwischen den Flüssig­keits­schichten, die mit unter­schied­lichen Geschwindig­keiten aneinander abgleiten.

Zusätzlich zu den verschie­denen Geschwin­dig­keits­vektoren gibt es einen Impuls­transport-Vektor _p, ähnlich wie bei einer bewegten Platte zu einer ruhenden Platte. Diese Impuls­transport­dichte pro Flächen­einheit, vermittelt dann die Kraft­wirkung zwischen den beiden Platten. Und das ist auch letzt­lich das, was man unter der Viskosität versteht. Der Impuls­transport führt nämlich zu der entspre­chenden Kraft­wirkung. Deshalb muss die obere Platte mit einer gewissen Kraft gezogen werden, um die Zähig­keit über­winden zu können.

Diese Kraft haben wir in der Hydro­dynamik schon aufge­schrieben als:

Wenn man das jetzt auf die Flächen­einheit der zwei Platten bezieht, ergibt sich:

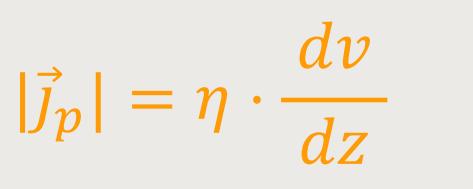
Es ist hierbei nur wichtig zu erkennen, dass es sich um einen Transport des Impulses der Teil­chen von der bewegten Zone hinunter in die ruhigere Zone handelt. Und das dieser Impuls­transport­vektor einfach nur Kraft pro Fläche ist.

Beim „Masse­transport” gibt es eine sehr ein­fache Gesetz­mäßig­keit. Hierzu könnte man sich wieder einen durch­gängigen Zylinder vor­stellen, wo in einem Bereich viele Moleküle vor­handen sind, dagegen in dem anderen Bereich nur wenige. Wenn man von Konvek­tions­bewegungen absieht, werden sich diese Moleküle auf eine gemein­same Konzen­tration aus­gleichen. Und hier ist jetzt die Abweichung der beiden Ausgangs­dichten ausschlag­gebend. Wenn die Dichte in beiden Bereichen jeweils gleich ist, wird sich maß­geblich nichts tun. Wenn die Dichte aber jeweils sehr unter­schiedlich ist, kommt es zu einem Transport vom Bereich hoher Dichte zum Bereich niedrigerer Dichte. Und der Masse­fluss­vektor pro Quer­schnitts­flächen­einheit, der zu dieser Diffusion beiträgt, lässt sich wie folgt beschreiben:

Das ist auch das Ficksche Gesetz.

D   ist der Diffusionskoeffizient
n   ist die Molekülanzahldichte

Je stärker der Gradient in dem Bereich mit der höheren Dichte ist, desto größer wird der Masse­fluss sein. Der Gradienten-Vektor zeigt immer in Richtung der höheren Parameter (Dichte), daher auch der negative Wert (minus). Denn das System diffun­diert immer in Richtung kleiner Dichten.

Der Diffusions­koeffizient ist eine Propor­tionali­täts­konstante, und ist nichts anderes als eine Größe, die charakte­ristisch für verschie­dene Gase ist. Je nach Molekül­größe, Quer­schnitt usw. werden die Bereiche schneller oder weniger schnell diffun­dieren. Und alles lässt sich empirisch ermitteln und wird letzt­lich durch den Diffusions­koeffi­zienten entspre­chend berück­sichtigt. Auf diese Wiese kann man den Masse­transport durch Diffusion bestimmen.

Der „Energie­transport” kann auf dreierlei Weise statt­finden.

Einer­seits durch Wärme­leitung. Hierbei geht es um ein ruhendes System, bei dem die Energie durch einen Stahl­stab von einem heißen Ende zum kalten Ende transpor­tiert wird. Als zweites durch Konvektion. Hierbei wird Materie durch ein strö­mendes Fluid, wie zum Beispiel ein heißes Gas, mit­geführt. Und letzt­lich sogar ohne Anwesen­heit von materiellen Körpern durch Strahlung. Die Energie, die uns beispiels­weise die Sonne liefert, gelangt weder durch Wärme­leitung noch durch Konvektion zu uns, sondern nur durch Wärme­strahlung. Und wie wir heute wissen, ist das nichts anderes, als eine elektro­magne­tische Welle, die eine der­artige Strahlung bewirkt.

Die „Wärme­leitung” kann man sich ähn­lich vor­stellen, wie es beim Masse­transport beschrie­ben wurde. Aber statt der unter­schied­lichen Molekül­dichten, herrscht jetzt auf der einen Seite eine hohe Tempe­ratur und auf der anderen Seite eine niedrigere. Die Moleküle auf der einen Seite zittern stark und die auf der anderen Seite weniger stark. Und dieses Zittern breitet sich dann langsam auf den ganzen Körper aus. Und in entspre­chender Weise erhält man auch hier eine Gesetz­mäßig­keit. In diesem Fall spricht man von einer Wärme­fluss­dichte :

K   ist die Wärmeleitfähigkeit

Die „Konvektion” ist ein hydro­dyna­mischer Vor­gang, bei dem eine gewisse Masse eines Gases oder einer Flüssig­keit durch die Strömung mit­geführt wird. Und mit dieser Masse oder Materie wird ein Wärme­inhalt trans­portiert. Dann spricht man von einem Energie­transport durch Konvektion.

Die thermische Strahlung oder Wärme­strahlung ist ein sehr wichtiger Prozess. Vor mehr als hundert Jahren hat Max Planck durch Analyse der Experi­mente zur Wärme­strahlung eines schwarzen Körpers erkannt, dass die Quanten­mechanik eine wesent­liche Rolle bei der Beschrei­bung dieses Effekts spielt. Er hat erst­mals in diesem Zusammen­hang eine soge­nannte Hilfs­konstante ℏ ein­geführt. Diese Hilfs­konstante hat sich in weiterer Folge als das Plancksche Wirkungs­quantum heraus­gestellt, und damit den Ausgangs­punkt der Quanten­physik markiert.

Die „Wärme­strahlung” lässt sich besonders einfach mithilfe des Stefan-Boltzmann-Gesetzes (nicht Ludwig Boltzmann) beschreiben.

Dieses Gesetz besagt, wie groß der Wärme­strahlungs­fluss von einer heißen Ober­fläche weg in die Umgebung ist. Beispiels­weise weg von der Sonnen­ober­fläche oder von einer rot­glühenden Metall­ober­fläche bzw. von einer ganz normalen Ober­fläche. Dieser Strahlungs­fluss Φ ist im wesent­lichen Energie pro Zeiteinheit, die von einer heißen Fläche aus auftritt. Der Strahlungs­fluss kann beschrieben werden als:

ε   ist der Emissionsgrad
σ   ist die Stefan-Boltzmann Konstante (5,7×10^-8 W/(m² ·K⁴))

Der Emissions­grad ist aus gewissen Gleich­gewichts­gründen das gleiche, wie der Absorp­tions­grad. Der Wert liegt nahe bei 1, denn schwarze Körper absorbieren gut und emittieren auch gut.

Die Wärme­strahlung von einer heißen Ober­fläche in die Umgebung, definiert als Energie pro Zeit­einheit, ist propor­tional zur Größe der Ober­fläche und auch propor­tional zu einem Theorie­faktor, nämlich dieser Stefan-Boltzmann Konstante.

⇦ Kapitel Kapitel ⇨