Die Thermo­dynamik gehört zu den Haupt­pfeilern der Physik. Nach­folgend wenden wir uns schwer­punkt­mäßig dem Energie­austausch in thermo­dyna­mischen Systemen zu. Denn gerade auf­grund thermo­dyna­mischer Gesetz­mäßig­keiten ist es mög­lich, Maschinen zu konstru­ieren, die es ermög­lichen Arbeit zu leisten.

Um aber Energie­über­gänge nach­voll­zieh­bar beschreiben zu können ist es sinn­voll, soge­nannte „Haupt­sätze in der Thermo­dynamik” einzu­führen. Dabei handelt es sich um grund­legende Sätze, die teil­weise auf den all­gemeinen und uns bereits bekannten Gesetz­mäßig­keiten beruhen. Diese Haupt­sätze basieren insbe­sondere auf der Energie­erhaltung. Es kommen teil­weise auch neue Aspekte hinzu, die in der Physik kleiner Systeme noch nicht vorhanden waren.

Einer­seits handelt es sich bei der Thermo­dynamik um ein in sich geschlos­senes Themen­gebiet. Anderer­seits hat es auch gewisse Schwie­rig­keiten in sich, weil man mit Größen kon­fron­tiert wird, die man zwar ein­deutig defi­nieren kann und die sich auch aus­rechnen lassen. Aber manches lässt keine unmittel­bare anschau­liche Inter­preta­tion zu, wie das bisher in der Physik der Fall war. Man muss sich damit ab­finden, dass man im Bereich der Thermo­dynamik mit Größen operiert, die nicht immer nach­voll­ziehbar sind. Wenn man noch keine konkrete Vor­stellung von gewissen Ab­läufen hat, kann man nur versuchen, intuitiv einen Bezug her­zuleiten.

Dennoch wollen wir die bisher gewon­nenen Erfah­rungen analy­sieren, die man im Zusammen­hang mit thermo­dyna­mischen Systemen und ins­besondere mit dem Energie­aus­tausch in thermo­dyna­mischen Systemen gewonnen hat. Und da hat sich heraus­kristal­lisiert, dass man mit Hilfe von drei Haupt­sätzen im Wesent­lichen die Dinge, die für den Energie­austausch in thermo­dyna­mischen Systemen wichtig sind, beschreiben kann. Die wollen wir jetzt nach­folgend Schritt für Schritt behandeln.

Als Basis der Betrach­tung werden wir zunächst einige Bezeich­nungen erläu­tern. Hierbei werden wir es mit „Zustands­größen” zu tun haben. Eine Zustands­größe ist eine makro­skopische Beschrei­bungs­größe für ein System, wie zum Beispiel der Druck, die Temperatur oder das Volumen eines Systems. Dies sind Größen, die einem System zukom­men, ohne dass man sagen muss, in welcher Weise und auf welchem Weg man zu diesem Zustand gelangt ist. Das trifft grund­sätz­lich auf alle Größen zu. So ist beispiels­weise die Wärme­menge Q keine Zustands­größe, denn man kann auf unter­schied­liche Weise zu bestimmten Zuständen kommen. Wenn man einem System Wärme zuführt, kann einer­seits die innere Energie U höher werden. Doch ein Teil dieser Wärme­menge kann auch in mecha­nische Arbeit umge­setzt werden.

Es besteht näm­lich ein Unter­schied, ob die Wärme komplett in innere Energie umge­setzt wird, ober ob ein Teil davon in mecha­nische Arbeit über­geführt wird. Insofern ist die Wärme­menge ein typi­sches Beispiel dafür, dass es auch Größen gibt, die keine Zustands­größen sind. Das ist ein gravie­render Punkt. Denn ohne Verständnis dieses Punktes kann man auch nicht ver­stehen, wieso es thermo­dyna­mische Maschinen gibt, die mecha­nische Arbeit leisten können.

Sowohl die Wärme­menge als auch die verrichtete Arbeit sind keine Zustands­größen. Es handelt sich hierbei viel­mehr um „Grenz­flächen­konzepte”. Denn über die Grenz­fläche eines Systems kann man eine gewisse Wärme­menge von außen nach innen trans­portieren. Und umge­kehrt kann man eine gewisse Arbeit ver­richten, die dieses System an die Um­gebung abgibt. Immer dann, wenn etwas in­einander umge­setzt wird, handelt es sich nicht um eine Zustands­größe.

Spricht man dagegen ein­deutig von einer Zustands­größe, sind diese Größen ent­weder propor­tional zur System­masse oder unab­hängig von der System­masse. Das heißt, es sind ent­weder extensive Größen, wie zum Beispiel das Volumen V eines Systems oder die innere Energie U eines Systems. Während der Druck p und die Temperatur T intensive Größen sind.

Des Weiteren kann auch ein thermo­dyna­misches Gleich­gewicht vorliegen. Darunter ver­steht man eine Situation, bei der die Zustands­größen in einem System, die dieses System be­schreiben, zeit­lich invariant sind.

Dann gibt es noch die Zustands­gleichung. Darunter ver­steht man eine Funktion der Größen f (p, V, T) = 0, die diese drei Größen mit­ein­ander im Gleich­gewicht ver­bindet. Für ideale Gase haben wir das schon be­trachtet. Und auch für reale Gase oder Flüssig­keiten lassen sich der­artige Zustands­gleichungen auf­stellen.

Eine letzte wesent­liche Erläu­terung betrifft die Ände­rung von Zustän­den. Also, wenn man von einem Zustand in einen anderen Zustand über­wechselt. Bei der­artigen Vor­gängen gibt es reversible und irreversible Zustands­ände­rungen. Man spricht von einer rever­siblen Zustands­ände­rung, wenn die zeit­liche Umkehr der äußeren Bedingungen, die zunächst zu der Zustands­änderung geführt haben, auch wieder zu einer Umkehr der Zustands­änderung führt. Das heißt, wenn man beispiels­weise in einem Kolben­zylinder den Kolben ein Stück heraus­zieht, dann hat man dadurch eine Zustands­änderung hervor­gerufen. Wenn man jetzt den Vor­gang umkehrt, indem man den Kolben wieder zurück­schiebt, bewirkt hat man somit die Umkehrung dieser Zustands­ände­rung. Bei einer der­artigen Zustands­ände­rung spricht man von einem „reversiblen” Prozess.

Dagegen kann man ein System in einem Zylinder betrachten, in welchem sich zum Beispiel ein Ventil befindet. Die eine Hälfte des Zylinders wurde mit Gas befüllt, und in der anderen Hälfte wurde ein Vakuum erzeugt. Öffnet man jetzt das Ventil, fließt das Gas ins Vakuum. Wenn man nach kurzer Zeit das Ventil wieder schließt, liegen in beiden Berei­chen die gleichen Druck­verhält­nisse vor. Würde man jetzt das Ventil wieder öffnen, wird das Gas nicht wieder zurück­fließen. Eine Umkehr der äußeren Bedin­gungen, die zu­nächst zur Zustands­ände­rung ge­führt haben, macht die Zustands­änderung nicht wieder rück­gängig. Dann spricht man von einem „irreversiblen” Prozess.

Aus zahlreichen experi­mentellen Erfah­rungen lässt sich dem­zufolge der „Erste Haupt­satz” der Thermo­dynamik fest­legen. Er gilt für beliebige Zustands­ände­rungen und besagt:

Die Summe der einem System zuge­führten Wärme und der einem System zuge­führten Arbeit ist gleich der Zunahme der inneren Energie dieses Systems.

ΔU   ist die Änderung der inneren Energie
ΔQ   ist die zugeführte Wärme
ΔW   ist die zugeführte Arbeit

Die innere Energie U ist eine Zustands­größe, also die Summe der Energien der einzelnen Moleküle in dem vor­handenen System. Dagegen sind die Größen ΔQ und ΔW Grenz­flächen­konzepte. Wie bereits erwähnt wurde, bleiben diese nicht separat in einem System erhalten, sondern gewisse Beträge werden von außen über die Grenz­fläche dem System zugeführt.

Abgeleitet aus diesem Haupt­satz erhebt man die Fest­stellung:

Es gibt kein Perpetuum mobile der ersten Art.

Darunter versteht man eine Maschine, die Arbeit verrichtet, ohne dass ihr von außen Energie zuge­führt wird, und ohne Ände­rung ihrer eigenen inneren Energie.

Dieser erste Haupt­satz ist natür­lich letzten Endes nichts anderes, als eine thermo­dyna­mische Verall­gemeine­rung des Energie­erhal­tungs­satzes. Aller­dings kommt jetzt zu der mecha­nischen Gesamt­energie zusätz­lich eine thermi­sche Energie hinzu. Denn die Gleichung bein­haltet in Erwei­terung des Energie­erhal­tungs­satzes eine Wärme­menge.

In der Mechanik wurde der Energie­erhaltungs­satz so formu­liert, dass bei konser­vativen Systemen die Summe von kinetischer und poten­tieller Energie erhalten bleibt. Aber für nicht­konser­vative Systeme gilt, wenn beispiels­weise Reibungs­kräfte vor­liegen, ist das nicht mehr zutref­fend. Solche Ein­schrän­kungen machen wir jetzt nicht mehr. Nun darf aufgrund von Reibungs­vor­gängen eine Wärme­menge ent­stehen, die nach­folgend mit berück­sichtigt wird. Durch die Hinzu­nahme der thermischen Energie gewinnt der Energie­erhaltungs­satz an Bedeutung, die er bei der Betrach­tung ein­facher Systeme in der Mechanik nicht hatte.

Auf diese Weise erhält man eine geschickte Verall­gemeine­rung des Energie­begriffs.

Was kann man jetzt mit diesem ersten Hauptsatz anfangen? Und was für verschie­dene Größen sind hier von Bedeutung?

Um das Thema Zustands­änderungen anschau­lich zu machen, werden wir nach­folgend einige spezielle thermo­dyna­mische Prozesse in idealen Gasen betrachten. Diese Prozesse lassen sich im All­gemeinen leicht nach­voll­ziehen. Und hier wird die zuvor behan­delte Wärme­kapa­zität wieder eine Rolle spielen. Wir behan­deln zunächst „isochore Prozesse”, also solche, bei denen das Volumen V = const bleibt.

Für ideale Gase gilt:

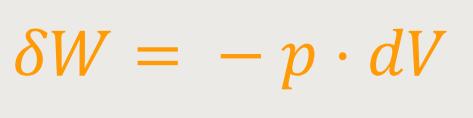
δW   ist die zugeführte Arbeit

Wenn man wie hier Arbeit zuführt, wird das System komprimiert, und damit wird das dV kleiner.

In der Gleichung steht sowohl δ als auch d , um anzu­deuten, dass es sich bei der Arbeit W nicht um eine Zustands­größe handelt. Dagegen ist das Volumen V sehr wohl eine Zustands­größe. Das δW ist viel­mehr eine gewisse Arbeits­menge, die zuge­führt wird. Sie lässt sich aber nicht dar­stellen als die Differenz zweier Arbeits­inhalte. Beim Volumen sieht das anders aus. Die Ände­rung des Volumens ist tat­säch­lich eine Ände­rung zwischen zwei Volumen­werten. Während dieses δW nicht als Ände­rung zwischen zwei Arbeits­inhalten auf­gefasst werden kann.

Man kann also einem System eine gewisse Arbeit zu­führen, und damit an dem System Arbeit leisten. Ander­seits kann dem System auch eine gewisse Wärme­menge zuge­führt werden. Das bedeutet aber nicht, dass damit der gesamte Wärme­inhalt oder Arbeits­inhalt ver­ändert wird. Denn die Wärme­menge und die Arbeit sind, wie mehr­fach erwähnt, keine Zustands­größen. Dagegen ist das Volumen sehr wohl etwas, was dem System zukommt, und stellt somit eine Differenz zweier Zustands­größen dar, einmal vor und einmal nach der Veränderung.

Wenn man das berück­sichtigt, lässt sich unter Bezug­nahme des ersten Haupt­satzes entspre­chend formu­lieren:

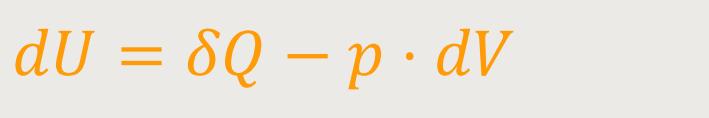
dU   ist die innere Energie (das Differential daraus)

Da das Volumen V = const bleibt, ergibt sich daraus, dass p · dV = 0, und dann gilt:

Das bedeutet wiederum, dass in diesem Fall die zugeführte Wärme­menge δQ voll­ständig zur Erhöhung der inneren Energie U ver­wendet wird. Da das Volumen konstant bleibt, kann das System keine mecha­nische Arbeit leisten. Dazu müsste sonst ein Kolben ver­schoben werden, wodurch eine Volumen­ände­rung hervor­gerufen wird. Das wurde aber als Vorgabe ausge­schlossen.

Wenn wir uns an die Betrach­tung der Wärme­kapa­zität erinnern, gilt ja für isochore Prozesse:

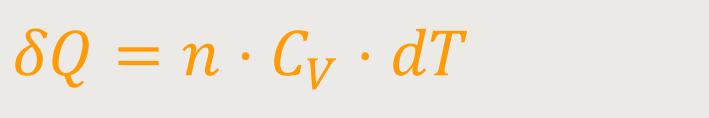
n   ist die Molzahl
C_V   ist die Molwärme

Das Produkt aus beiden ist die Wärme­kapazität.

In Erweiterung erhält man bei konstantem Volumen:

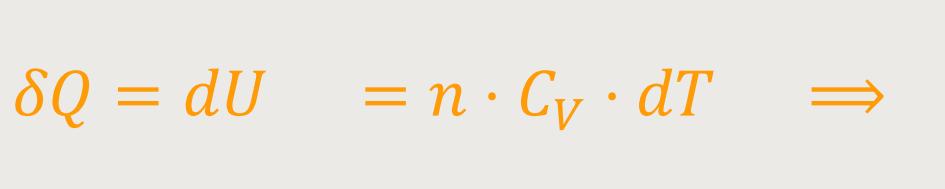
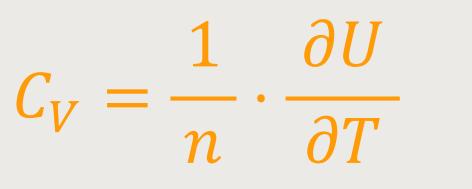
Die Molwärme ergibt sich durch Differen­tiation der Zustands­größe U, also der inneren Energie nach der Tempe­ratur. Hier ist es partiell ausge­drückt, weil die innere Energie auch von anderen Eigen­schaften abhängig sein kann. Bei idealen Gasen aller­dings ist sie im All­gemeinen nur von der Tempe­ratur abhängig.

Zusammen­fassend kann man bezogen auf diese Zustands­änderung sagen, dass wenn man bei isochoren Systemen eine Wärme­menge zuführt, sich diese komplett in der Vergröße­rung der inneren Energie wieder findet.

Im Gegen­satz dazu betrachten wir jetzt „isobare Prozesse”. Bei isobaren Prozessen ist es so, dass der Druck p = const bleibt. Auch hier legen wir wieder den ersten Haup­tsatz (s.o.) zugrunde:

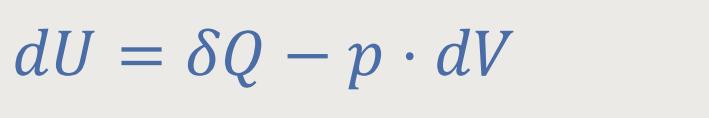
Wenn man einem System, bei dem der Druck konstant gehalten wird, eine Wärme­menge zuführt, dann wird einer­seits die Tempe­ratur zunehmen, aber anderer­seits wird das System auch expan­dieren. Also die Zuführung von Wärme­mengen bewirkt zweier­lei. Einer­seits führt sie teil­weise zu einer Erhöhung der Tempe­ratur und damit zu einer Erhöhung der inneren Energie. Anderer­seits wird sie teil­weise in eine Abgabe von mecha­nischer Arbeit umgesetzt.

Dieser Vorgang lässt sich zunächst nur etwas kompli­zierter aus­drücken. Man ist aber bestrebt, es dennoch in einer ver­gleichbar ein­fachen Weise dar­zustellen. Sodass man sagen kann, die zuge­führte Wärme­menge wird auch hier voll­ständig zur Erhöhung einer bestimmten thermo­dyna­mischen Größe verwendet.

Um das darstellen zu können, führt man den Begriff der „Enthalpie” ein. Diese Enthalpie H ist auch eine Art innere Energie und eben­falls eine Zustands­größe. Ihre Beziehung lautet:

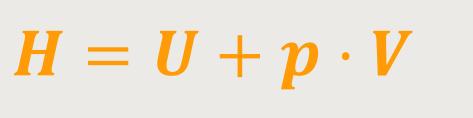
Die Enthalpie kann einen Prozess wieder aus­gleichen. Dass, was man bei einem isobaren Prozess beobachtet, nämlich dass es teil­weise zu einer Erhöhung der inneren Energie kommt und teil­weise mecha­nische Arbeit abge­führt wird, bringt die Enthalpie wieder in Ordnung. Mit anderen Worten, die zuge­führte Wärme­menge wird komplett in eine Erhöhung der Enthalpie um­gesetzt. Warum legt man so viel Wert auf diese Formulierung?

Das hat mit den Arbeits­bedingungen der Chemiker zu tun. Beim Durch­führen von chemischen Reaktionen im Labor wird unter konstantem Druck gearbeitet, näm­lich unter dem normalen Atmo­sphären­druck. Meistens liegen dabei isobare Bedin­gungen vor und keine isochoren Bedin­gungen. Auf das Reagenz­glas wirkt immer der normale Luft­druck der Atmo­sphäre. Und wenn chemische Reaktionen ablaufen, bleibt der Gesamt­druck des Systems konstant. Es gibt sicher­lich auch Aus­nahmen, aber in der Regel wird unter isobaren Bedingungen experi­mentiert.

Um eine möglichst ein­fache Argumen­tation zu finden, benötigt man die Beziehung der Enthalpie. Wenn man den Forma­lismus der Enthalpie kennt, lässt sich ihr Differen­tial bilden:

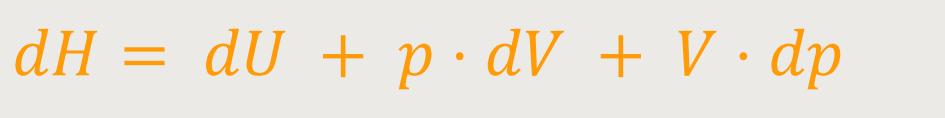
Und da bei den isobaren Prozessen der Druck p = const bleibt, ist entspre­chend V · dp = 0.

Zu Beginn hatten wir bereits formuliert, dass:

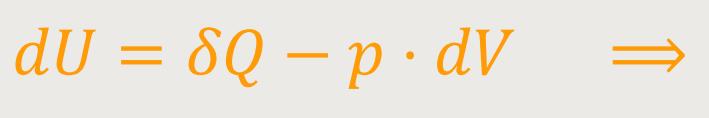
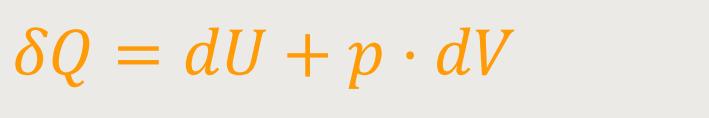
Durch Einsetzen erhalten wir:

Und damit erhält man etwas Ähn­liches, wie bei der inneren Energie. Analog zu oben kann man eine ver­gleich­bare Schluss­folge­rung ziehen: Die zuge­führte Wärme­menge δQ wird voll­ständig zur Erhöhung der Enthalpie H verwendet.

Deshalb spricht man in der Chemie auch oft von einer „Reaktions­enthalpie”. Wenn bei konstantem Druck bei irgen­deiner Reaktion eine Wärme­menge auf­tritt, dann lassen sich die daraus ergebenden Zustands­ände­rungen am besten durch die Enthalpie­änderung beschreiben. Denn die Enthalpie­änderung ist ent­spricht der zuge­führten Wärme­menge.

Abschließend kann man ähn­lich wie bei den isochoren Prozessen noch definieren, wie sich die zuge­führte Wärme­menge δQ mithilfe der Molwärme bei konstantem Druck darstellt:

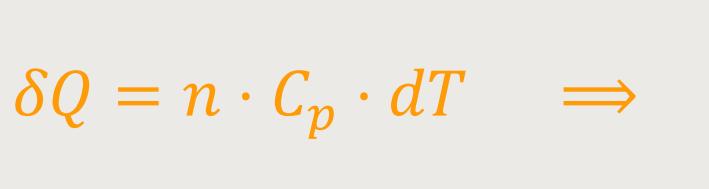
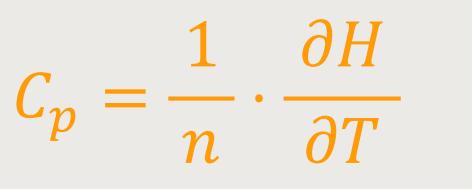
Die Molwärme ergibt sich durch Differen­tiation der Zustands­größe H, also der Enthalpie nach der Tempe­ratur. Das ist zunächst alles, was sich an dieser Stelle über die Enthalpie sagen lässt.

Jetzt werden wir „isotherme Prozesse” betrachten. In diesem Fall gilt für die Tempe­ratur, dass T = const bleibt. Am ein­fachsten lässt sich das nach­voll­ziehen, wenn man sich ein System in einem Wärme­bad vor­stellt. Auch hier erhält man nach dem Ersten Hauptsatz in entsprec­hender Weise (s.o.):

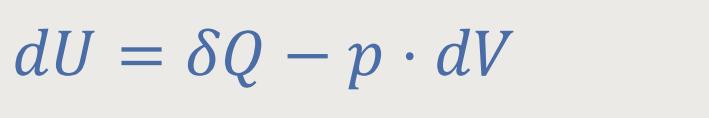
Und da wir bereits einige Terme aus der Defini­tion der Tempe­ratur kennen, ergibt sich damit:

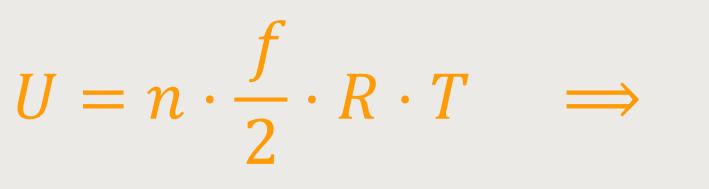
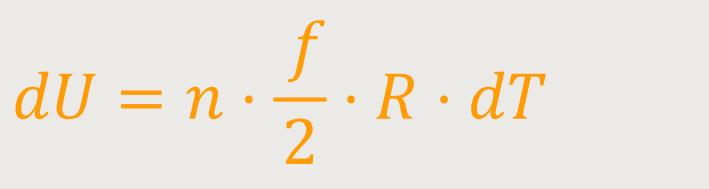
Hinweis: Man könnte auch N · (f /2) · K · T schreiben, aber für viele prak­tische Anwen­dungen ist es vorteil­hafter, die Beziehung mit der Molzahl n und der Gaskons­tanten R dazustellen.

Weil die Tempe­ratur konstant ist, gilt entspre­chend dT = 0. Und dadurch erhält man:

Wird die Tempe­ratur in dem System konstant gehalten, bleibt auch die innere Energie des Gases konstant. Im Grunde eine ganz ein­fache Beziehung. Denn die Tempe­ratur beschreibt ja die kinetische Energie pro Molekül. Wenn also die Tempe­ratur konstant bleibt, bleibt die mittlere kinetische Energie pro Molekül eben­falls konstant. Und daher auch in Summe über alle Moleküle.

Wenn aber dU = 0 ist, heißt das wiederum:

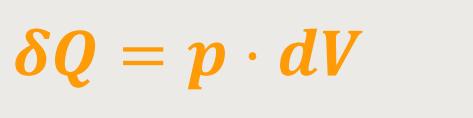
Daraus kann man wieder eine unmittel­bare Schluss­folgerung ziehen. Näm­lich, dass die zuge­führte Wärme­menge δQ voll­ständig in Arbeit −δW umge­wandelt wird. Und wenn die Tempe­ratur konstant bleibt, erhält man wegen der Gültig­keit der Zustands­gleichung:

Wir erinnern uns, wenn man das grafisch in einem p-V-Diagramm umsetzt, ent­spricht das den Isothermen des idealen Gases.

⇦ Kapitel Kapitel ⇨