Im vor­herigen Kapitel hatten wir die Gas­konstante definiert. In der Chemie wird in diesem Zusammen­hang meistens über mol gesprochen. Aber in der Physik hat sich der Begriff des kmol durch­gesetzt. Und da man sich in der Physik auf die SI-Einheiten bezieht, jedoch die Massen­einheit das kg ist, wird deshalb das kmol als Einheit verwendet.

Wobei 1 kmol die­jenige Menge einer Substanz ist, in der so viele Moleküle vor­handen sind, wie in 12 kg vom Kohlen­stoff­isotop 12C. Wie viele Moleküle sind das in etwa? Die Anzahl ist die soge­nannte „Avogadro-Konstante”:

Demnach ent­spricht 1 kmol irgen­deiner Substanz so vielen Molekülen wie diese Konstante aussagt. Und wenn man die Menge irgen­deiner Substanz kennt, kann man diese durch die Molzahl n beschreiben.

Das ist ein­fach die Anzahl Mole, die in dem konkreten System vor­handen sind. Und dem­zufolge gilt für die Molekül­anzahl:

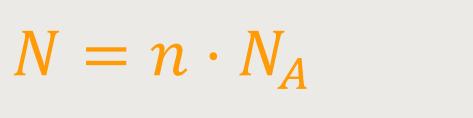
N   ist die Molekülanzahl

Wenn man jetzt die Zustands­gleichung entspre­chend umformuliert, ergibt sich:

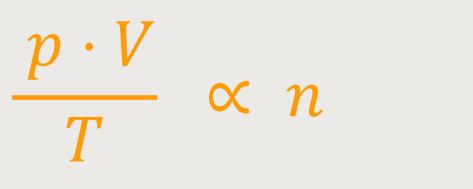
Diese Propor­tionalitäts­konstante gilt immer, egal welches Material man ver­wendet. Ob das jetzt Helium ist oder Stick­stoff oder was auch immer. Dem­entspre­chend kann man auch schreiben:

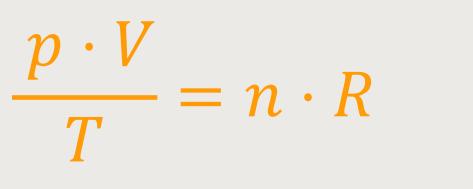
R   ist eine universelle Gaskonstante

Diese all­gemeine Gas­konstante lässt sich auch experi­mentell bestimmen:

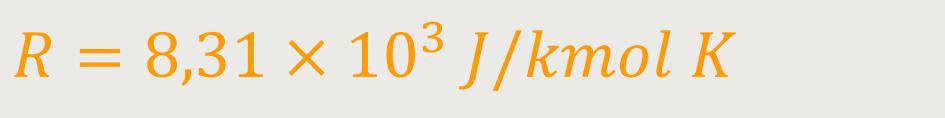
Wenn man das entsprechend wieder umformt und gleich­zeitig für n einsetzt, ergibt sich:

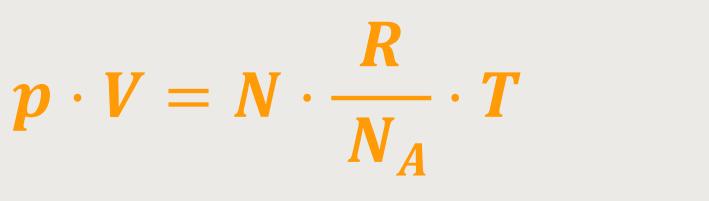
p · V entspricht also der Anzahl Moleküle N in dem System, multi­pliziert mit einer Konstanten und dies multi­pliziert mit der Tempe­ratur. Diese durch Umformung entstandene Konstante R /N_A wird sich im weiteren Verlauf als die berühmte Boltzmann-Konstante heraus­stellen. Letzt­lich wird ein ideales Gas so definiert, dass es dieser Gleichung genügt.

Jetzt werden wir kurz die „Wärme­menge” betrachten. Wenn man die Tempe­ratur eines Körpers erhöhen möchte, muss eine gewisse Wärme­menge zugeführt werden. Hat man zum Beispiel einen kleinen Topf mit Wasser, muss nur wenig Wärme zuge­führt werden. Wenn man dagegen einen großen Topf hat, muss man entspre­chend mehr Wärme zuführen. Wenn eine Temperatur­erhöhung um ΔT erreicht werden soll, muss eine Wärme­menge ΔQ zuge­führt werden. Hierbei ist ΔQ ∝ ΔT.

Wenn man beispiels­weise die Tempe­ratur um 2 °C erhöhen möchte, muss die doppelte Wärme­menge zugeführt werden. Diesen Propor­tionalitäts­faktor sieht man generell als „Wärme­kapazität” an:

Γ (Gamma)   ist die Wärme­kapazität des betrachteten Körpers

Je größer der Körper ist, desto mehr Wärme muss zugeführt werden, um eine bestimmte Tempe­raturer­höhung zu erreichen. Diese Wärme­kapazität steht mit der Masse des Köpers in Wechsel­beziehung. Wenn der Körper mehr Masse hat, hat es auch eine höhere Wärme­kapazität.

Wie lässt sich diese zuge­führte Wärme­menge konkret messen? Zunächst bietet es sich an, die Ein­heit fest­zulegen. Historisch bedingt hatte man sich über­legt, dass es die­jenige Wärme­menge ist, die man benötigt, um die Temperatur von 1 kg Wasser um 1 K zu erhöhen. Diese Wärme­menge ent­spricht dann 1 kcal. Es ist eine extensive Größe, die sich propor­tional zur Masse verhält. Die Wärme­kapazität hat somit die Einheit [kcal /K].

Später werden wir noch sehen, dass man diese Wärme­kapazität auch auf die Massen­einheit oder auf 1 mol beziehen kann. Dadurch erhält man die spezifische Wärmekapazität.

Doch was versteht man eigent­lich unter der Wärme? Früher dachte man, es sei ein Fluidum, das in die Materialien hinein­geht. Aber bereits 1845 hat J. P. Joule dazu bei­getragen, dem Thema eine andere Sicht­weise zu ver­mitteln. Joule hatte die Idee, dass man diese Wärme­menge, die man einem Material zuführen kann, nicht nur durch Erwärmen erreichen kann, sondern auch durch Reibung. Reibung wird dadurch erzeugt, dass man eine Arbeit verrichtet.

Wie die Wärme­zufuhr letztlich erfolgt, ist dem­nach egal. Das kann somit auch mithilfe von mecha­nischer Energie erfolgen. Egal, für welche Vorgehens­weise man sich ent­scheidet, beides ist stets zueinander proportional.

Wird die Wärme­menge durch mecha­nische Energie zugeführt, ergibt sich für die Arbeit:

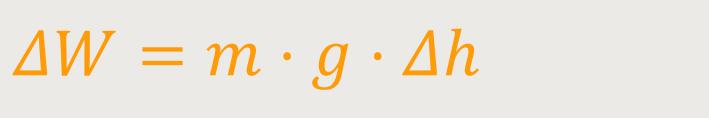
ΔW   ist die verrichtete Arbeit

Es stellt sich heraus, dass die Wärme­menge stets propor­tional zur ver­richteten Arbeit ist.

K_W   ist ein Proportionalitäts­faktor

Der Propor­tionalitäts­faktor wird auch als das Wärme­äquivalent bezeichnet. Diese Größe bleibt immer die gleiche, egal was für eine Substanz man verwendet. Sie ist definiert als:

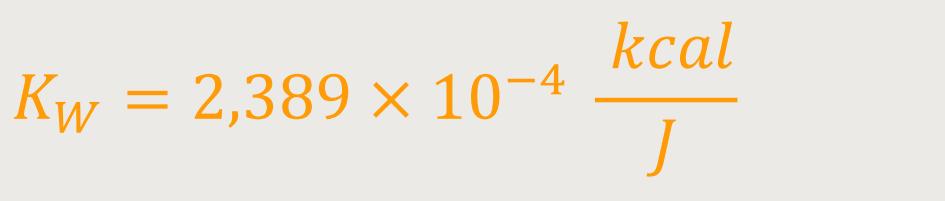
Auch das ist eine univer­selle Konstante, die sich experi­mentell bestimmen lässt.

Bei genauer Betrachtung erkennt man, dass die Wärme, die zuge­führt wird und die Arbeit, die verrichtet wird, das gleiche ist. Wie lässt sich das unter­mauern? Eine Hilfe dabei ist, den moleku­laren Charakter der Materie zugrunde zu legen. Nehmen wir der Einfach­heit halber eine Flüssig­keit her, die aus zahl­losen Molekülen besteht. Wird jetzt diese Flüssig­keit durch einen Rühr­stab in Bewegung versetzt, wird die von außen geleistete Arbeit in der Flüssig­keit umgesetzt. Die Arbeit wird quasi über­tragen in die unge­ordnete Bewegung der Flüssig­keits­moleküle.

Hat man beispiels­weise eine konvektive Bewegung einer Flüssig­keit, dann ist die Energie in dem System geordnet. Wenn aber die Flüssig­keit durch Reibung zum Still­stand kommt, dann ist die Energie nicht verloren gegangen, sondern sie wurde umgesetzt in eine Erhöhung der Energie der ungeordneten Bewegung der Flüssig­keits­moleküle. Dementspre­chend lässt sich folgende Schluss­folgerung ziehen:

Wärme ist die Energie der ungeordneten Bewegung der Moleküle eines Körpers.

Insofern kann man die Wärme­menge als kinetische Energie auf­fassen. In diesem Fall benötigt man keine eigene Einheit mehr für die Wärme­menge. Man misst sie einfach als kinetische Energie. Das bedeutet wiederum, dass auch der Propor­tionalitäts­faktor überhaupt nicht benötigt wird. Wenn man aufgrund der experimentellen Befunde erkennt, dass die beiden Größen, Wärmemenge und Energie, wesensgleich sind, dann kann man den Faktor einfach dimensionslos setzen:

Es ist nur eine Frage der Ein­heiten­festlegung. Wir erinnern uns, die Einheit für die Wärme­menge ΔQ wurde in Kalorie fest­gelegt. Wobei 1 kcal über die Aufwärmung von Wasser definiert wurde. So kann man jetzt nicht mehr vorgehen. Sondern wenn dieses K_W ≡ 1, dann bedeutet das:

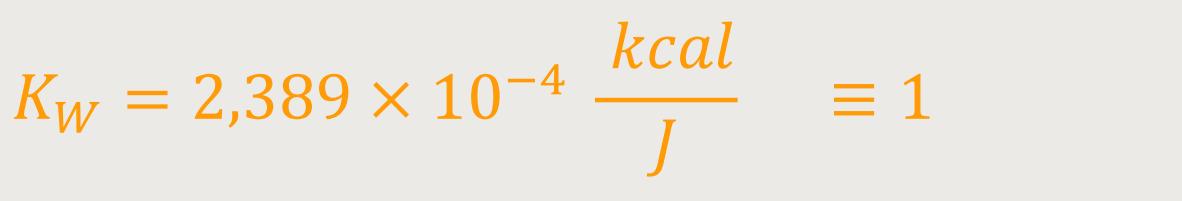
Was ergibt sich daraus, wenn man diesen Weg beschreitet? Dann lässt sich sofort 1 kcal aus­rechnen:

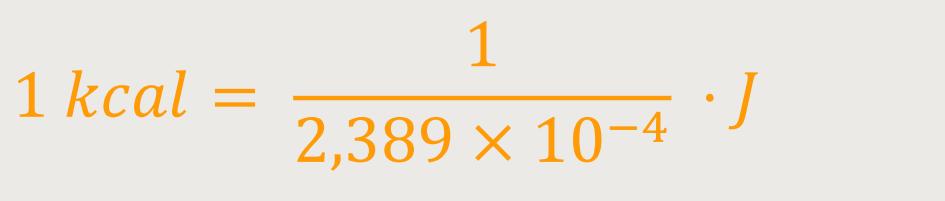
Damit wird die absolute Basiseinheit der Wärmemenge degradiert zu einer inkohärenten Energieeinheit. Die kcal kann nach wie vor verwendet werden, als Einheit der Energie oder Wärmemenge. Trotzdem bleibt man natürlich bei J als der SI-Einheit für die Energie oder Arbeit. Und damit ergibt sich jetzt ein Faktor von 4.185,85. Das heißt, 1 kcal sind fast 4.200 J (Joule).

Jetzt lässt sich auch nachvollziehen, warum so viel Arbeit verrichtet werden muss, um zum Beispiel 1 kg Wasser wenigstens um 1 K (Kelvin) zu erhöhen. Gerade bei Wasser stellt sich heraus, dass es im Verhältnis pro Masseneinheit eine sehr hohe Wärmekapazität hat.

Ein Medium aus Gas kann man sich zusammen­gesetzt aus einzelnen Molekülen vor­stellen. Diesen Molekülen kann man auch soge­nannte „Freiheits­grade” zuordnen. Das sind Freiheits­grade der Trans­lation, der Rotation und der Schwingung. Ein Molekül kann sich somit in drei Raum­richtungen trans­latorisch fort­bewegen, es kann sich aber auch um drei Achsen drehen und es kann Schwingungs­vorgänge durch­führen. Wir wollen diese Freiheits­grade aber unter dem Aspekt idealer Gase betrachten.

In diesem Zusammen­hang legen wir gewisse Voraus­setzungen fest. Wir werden die Moleküle praktisch als punkt­förmig annehmen, und sie sollen auch keine inneren Schwingungen haben. Damit bleiben für diese Moleküle nur die drei Freiheits­grade der trans­latorischen Bewegung übrig. Andere werden wir hier jetzt nicht betrachten. Unter sehr all­gemeinen Voraus­setzungen verteilt sich die Molekül­energie im Mittel gleich­mäßig auf alle Freiheits­grade. Wie kann man jetzt die Gas­eigen­schaften mit einem der­artigen Modell beschreiben?

Aus der Punkt­mechanik kennen wir bereits den Ausdruck, dass die Kraft als die zeit­liche Ableitung des Impulses dar­gestellt werden kann:

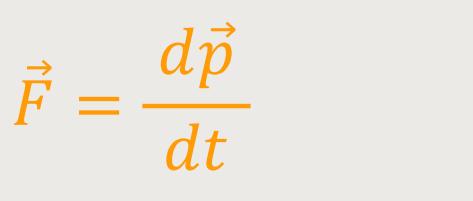
Möchte man solche Punkt­massen weiter beschreiben, kann man die Kraft, die von einem solchen Gas ausgeübt wird, auch als einen Impuls­über­trag fest­legen. Wenn wir beispiels­weise einen Behälter betrachten, dann bewirkt die Kraft eines Gases auf die Innen­ober­fläche des Behälters einen Impuls­über­trag. Wenn so ein Teilchen mit einem Impuls gegen eine Wand­fläche trifft, kann es zu einem elastischen Kontakt kommen. Dann fliegt es mit dem gleichen Impuls wieder in der Gegen­richtung zurück. Das heißt, das Teilchen hat zweimal den Impuls auf die Ober­fläche über­tragen. Von +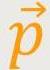 hat es auf − 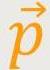gewechselt. Das bedeutet, um zwei 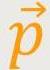hat es sich geändert. Diese zwei 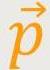wurden auf die Grenz­fläche über­tragen. Somit wurde eine Kraft auf diese Fläche aus­geübt.

Dementspre­chend kann man den Druck des Gases, der auf eine derartige Fläche wirkt, beschreiben als:

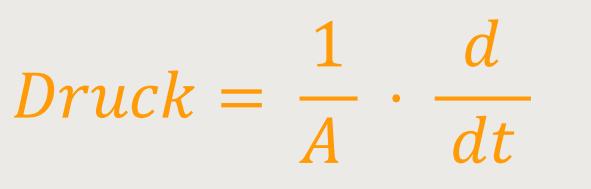
A   ist die Oberfläche

Dazu hat Daniel Bernoulli verschiedene Unter­suchungen gemacht. Und mit seinen Überlegungen lassen sich einige Bezeich­nungen fest­legen (siehe unten):

Obige Gleichung beinhaltet den auf die Fläche über­tragenen Impuls. Was versteht man unter dieser Größe?

Nehmen wir zum Beispiel ein Molekül in einem Volumen, welches sich in der Nähe einer Oberfläche aufhält. Dieses Molekül kann sich trans­latorisch zu allen Seiten der drei Raum-Richtungen bewegen. Letztlich wird das Molekül aber nur 1/6 aller seiner Bewegungen in Richtung der Ober­fläche durch­führen.

Nun greifen wir uns einen Teil­bereich dieser Ober­fläche heraus, und bezeichnen diesen Flächen­ausschnitt mit A. Das Molekül bewegt sich mit der Geschwindig­keit auf diese Teil­fläche zu. Aus dieser 2-dimen­sionalen Teil­fläche denkt man sich jetzt im Vorder­grund einen räum­lichen Quader. Inner­halb dieses Quaders werden alle darin befind­lichen Moleküle in der Zeiteinheit t auf diese Teil­fläche treffen. Somit wird die Höhe dieses Quaders mit v · t definiert.

Gleichzeitig erhält man die Stoßan­zahl der Moleküle auf die Fläche A in der Zeit t. Das sind nämlich alle Moleküle in dem Quader, die sich gerade um diese Strecke v · t bewegen. Daraus ergibt sich die Gleichung:

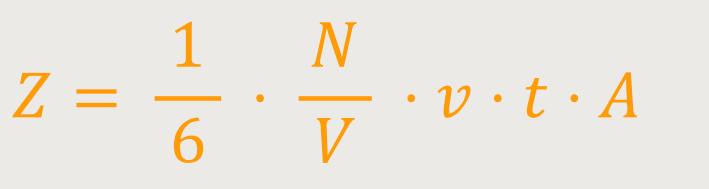
Z   ist die Stoßanzahl der Moleküle
v · t · A   ist das Volumen des Quaders

Nach statis­tischen Abschät­zungen beträgt die Stoß­anzahl somit 1/6 der Anzahl aller Moleküle im Quader. Damit erhält man den auf die Ober­fläche A über­tragenen Impuls. Der Impuls­über­trag für 1 Molekül ist demnach:

m · v   ist der Impuls des Moleküls

Das Molekül trifft zunächst auf die Ober­fläche und geht anschlie­ßend mit dem gleichen Impuls wieder in der Gegen­richtung zurück.

Dementspre­chend ist der Impuls­übertrag für alle Moleküle:

Wenn man in die Gleichung für den Druck entsprechend einsetzt, ergibt sich:

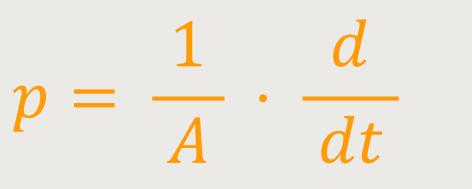
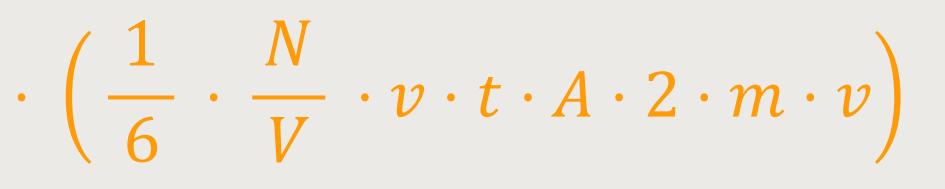
A   ist die jeweils betrachtete Teilfläche

Letzt­lich ver­bleibt nach Weg­kürzen in der Gleichung:

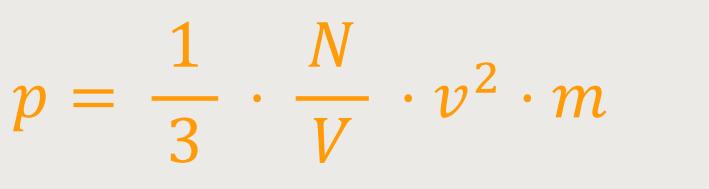
Das ist der instantane Druck aufgrund des Impuls­übertrages.

Abschlie­ßend führt man noch eine Mittelung durch, weil sich die Geschwin­dig­keit der Moleküle noch während der Bewegung ändern wird. Dann erhält man entspre­chend der fest­gelegten Bezeich­nungen:

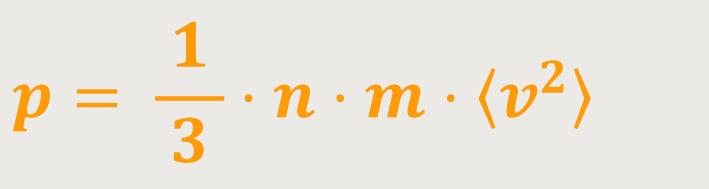
Das ist die berühmte Grund­gleichung von Daniel Bernoulli.

⟨ v²⟩   ist das Quadrat der mittleren Geschwindig­keit der Moleküle

Diese Beziehung ist die entschei­dende Ausgangs­bedingung für die statis­tische Inter­pretation der Bewegung der Gas­moleküle und letzt­lich der Temperatur.

⇦ Kapitel Kapitel ⇨