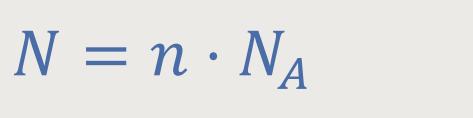Um das Thema Wärme­kapazität anschau­lich zu machen, stellt man sich gedank­lich einen Paraffin­block vor, und dazu zwei Metall­zylinder mit gleichen Abmessungen. Der eine Metall­zylinder besteht aus Blei, der andere aus Stahl, wobei der Blei­klotz natürlich schwerer ist. Beide Zylinder werden in kochendem Wasser auf 100°C erhitzt. Anschlie­ßend werden beide auf den Paraffin­block gestellt.

Jetzt geht es darum zu ermitteln, wie groß die in dem jewei­ligen Metall­zylinder gespeicherte Wärme­energie ist. Wenn der eine Zylinder eine deutliche höhere Wärme­energie hat als der andere, wird er auch tiefer in das Paraffin einsinken. Zunächst würde man erwarten, dass das Blei aufgrund seines Gewichtes tiefer einsinken wird. Aber Experimente zeigen, dass viel­mehr der Stahl­zylinder tiefer einsinkt.

Generell gilt daher, dass die Aufnahme­fähig­keit von Körpern, was ihre Wärme­mengen angeht, bei verschie­denen Materialen unter­schiedlich groß ist. Dass ein solcher Unter­schied besteht, kann mit Hilfe der Wärme­kapazi­tät beschrieben werden. Wir hatten diese schon einmal definiert:

Γ (Gamma)   ist die allgemeine Wärme­kapazität des betrachteten Körpers

Die Wärme­kapazität ist ein konstanter Faktor. Demnach ist die Wärme, die man in einen Körper hinein­steckt, propor­tional zur Änderung der Tempe­ratur. Gibt man doppelt sowie Wärme in den Körper hinein, dann wird auch die Tempe­ratur­erhöhung doppelt so groß sein. Und das führt dazu, dass man sich ent­weder auf die Massen­einheit (kg) oder auf die Einheit mol bezieht. Und so lässt sich einer­seits eine spezifische Wärme­kapazi­tät definieren:

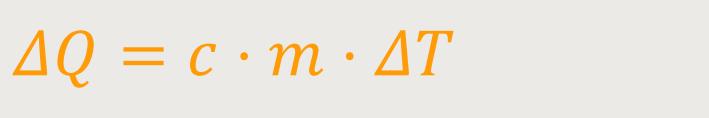
Das ist die Wärmekapazität pro Masseneinheit.

c   ist die spezifische Wärmekapazität
m   ist die Masse des Systems

Multi­pliziert mit der Masse des Systems erhält man die spezi­fische Wärme­kapazi­tät, auch „spezifische Wärme” genannt. Je größer die Masse ist, desto mehr Wärme muss zugeführt werden, um die Temperatur um ein ΔT zu erhöhen. Und die Wärme­kapazi­tät belegt entspre­chend, dass dies bei verschie­denen Materialien unter­schiedlich ist.

Alternativ dazu definiert man die Molare Wärmekapazität:

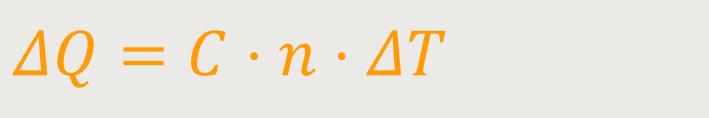
C   ist die Molare Wärme­kapazität (auch Mol-Wärme genannt)
n   ist die Molzahl des betrachteten Systems

Nachdem wir uns das noch­mals kurz in Erinnerung gerufen haben, können gehen wir einen Schritt weiter. Wie bereits erwähnt, lässt sich die Temperatur inter­pretieren, als ein Maß für die mittlere kinetische Energie pro Freiheits­grad des Moleküls. Wenn man weiß, wie viel kinetische Energie in einem Molekül enthalten ist, können weitere Berech­nungen durch­geführt werden. Wir gehen wieder von idealen Gasen aus, sprich es gibt keine Wechselwirkungen zwischen den Teilchen. So gelangt man schließlich auf die innere Energie eines idealen Gases, die wie folgt definiert ist:

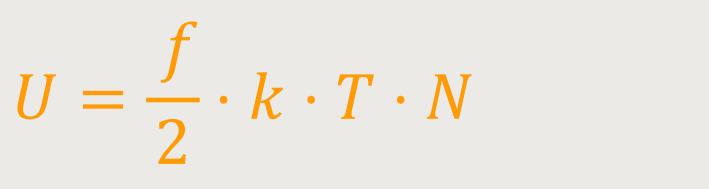
f   ist die Anzahl der Freiheitsgrade
N   ist die Gesamtanzahl der betrachteten Moleküle

Die innere Energie ist gleich der kinetischen Energie für 1 Molekül, multi­pliziert mit der Anzahl der Moleküle. Auf diese Weise lässt sich die Temperatur mithilfe der kinetischen Energie der Gas­moleküle oder irgend­welcher anderen Moleküle sehr einfach inter­pretieren.

Und jetzt kann man noch eine einfache Umformung machen. Hierzu erinnern wir uns:

Dementsprechend erhält man:

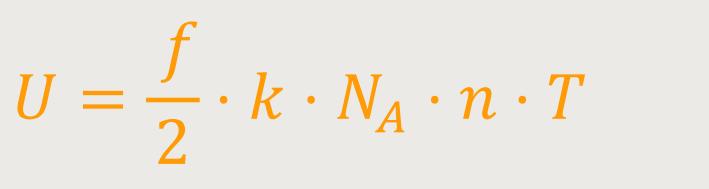
Und dieses k · N_A ist die all­gemeine Gas­konstante R, die wir bereits von der Zustands­gleichung her kennen. Und damit ergibt sich:

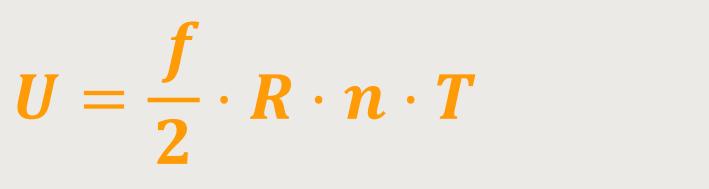
Das ist die gesamte innere Energie eines idealen Gases.

Mit diesem Ausdruck kann man unmittel­bar aus­rechnen, wie viel Wärme man zuführen muss, um eine Tempe­ratur­änderung zu bewirken.

Die absolute Temperatur T ist ein Maß für die mittlere kinetische Energie eines Moleküls in dem entspre­chenden Körper. Die Temperatur zeigt an, wie hektisch die Moleküle in einem Körper unter­wegs sind. Wenn man diese kinetische Energie eines Moleküls in einem Körper kennt, dann ist es ein geringer Aufwand, die gesamte innere Energie der ungeord­neten Molekül­bewegungen in dem Körper zu ermitteln.

Immer voraus­gesetzt, man hat gleich­artige Moleküle. Denn wir gehen zunächst immer nur von homogenen ein­fachen Systemen aus. Wenn man eine Mischung von mehreren verschie­denen Substanzen hat, muss das entspre­chend aufsummiert werden. Doch in unserem Fall gehen wir von einer Substanz mit nur einer Art Molekülen aus.

Wenn man weiß wie groß die mittlere kinetische Energie der ungeord­neten Molekül­bewegung für 1 Molekül ist, wird das einfach multi­pliziert mit der Anzahl der Moleküle in dem Körper und man erhält dann die innere Energie, wie das bereits oben gezeigt wurde.

Was passiert, wenn man eine Zustands­ände­rung bei einem solchen idealen Gas durch­führt? Das kann zum Beispiel in Form einer Wärme­zufuhr geschehen, wobei das Volumen dieses Gases V = const, also unver­ändert bleibt. So etwas nennt man auch einen „isochoren Prozess”. Die Wärme­zufuhr ΔQ geht dann voll­ständig in die innere Energie des Systems über:

Wenn man voraus­setzt, dass sich das Volumen nicht ändert, wird von diesem System auch keine mecha­nische Arbeit geleistet. Denn nur wenn sich ein Volumen ändert, kommt es zu einer Arbeits­leistung. Daher verbleibt die Wärme voll­ständig in Form der inneren Energie in dem System. Und die Änderung der inneren Energie ΔU kann man sofort aufschreiben als:

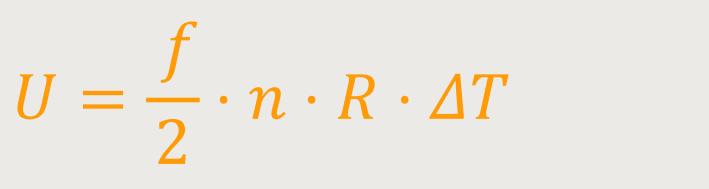
Weiter oben haben wir bereits die spezi­fische und die molare Wärme­kapazi­tät betrachtet.

Die Molare Wärme­kapazität, oder auch „Mol-Wärme” genannt, war bereits (s.o.) definiert als :

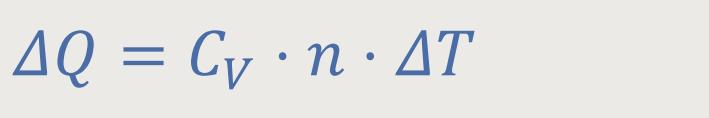
Jetzt schreibt man C_V, weil das Volumen konstant bleibt.

Wenn man beide Beziehungen gleich­setzt und anschlie­ßend umformt, ergibt sich entspre­chend:

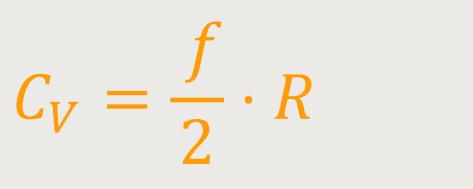
Sowohl die molare Wärme­kapazität als auch die Gas­konstante kann gemessen werden. Auf diese Weise lassen sich auch die Anzahl der Frei­heits­grade ermitteln. Und so erhält man aus einfachen makro­skopischen thermo­dyna­mischen Mess­werten letzt­lich mikro­skopische Informa­tionen. Denn die Anzahl der Frei­heits­grade gibt Informa­tionen darüber, wie viel Trans­lations­frei­heits­grade ein Molekül hat bzw. ob es rotieren kann oder ob es schwingen kann.

Mit dieser relativ ein­fachen Beschrei­bung der Thermo­dynamik erhält man sogar einen direkten Zugang zu Quanten­effekten. Denn aufgrund der Abnahme der Tempe­ratur werden zunehmend mehr und mehr Frei­heits­grade einge­froren. Sprich, es muss eine gewisse Mindest­energie vor­handen sein, um bestimmte Freiheits­grade über­haupt anzuregen. Und wenn die Tempe­ratur kleiner wird, ist auch die thermische Energie kleiner. Oder anders ausgedrückt, es können zunehmend weniger von den vorhan­denen Freiheits­graden angeregt werden, weil deren untere Energie­schwelle zu hoch ist. Erst durch die Quanten­physik hat man eine konkrete Mög­lich­keit erhalten, das zu inter­pretieren.

Alternativ dazu kann man auch die Wärme­zufuhr für den Fall betrachten, dass der Druck p = const bleibt. Dazu stellt man sich gedank­lich wieder ein Gas­volumen in einem Zylinder vor, in welchem sich ein Kolben bewegen kann. Wenn man jetzt Wärme zuführt, dehnt sich das Gas entspre­chend aus, und der Kolben leistet Arbeit. Obwohl der Druck konstant bleibt, passieren also zwei Dinge. Erstens wird bei der Wärme­zufuhr ΔQ die innere Energie zunehmen. Man kann auch von einer Zufuhr von Energie ungeord­neter Molekül­bewegungen sprechen. Zweitens bewegt sich der Kolben, was bedeutet, er verrichtet Arbeit −ΔW.

Hierbei gilt, dass Größen­differenzen, die dem System zuge­führt werden, einen positiven Wert haben. Wogegen alles, was vom System abge­führt wird, einen negativen Wert hat. Insofern wird die Arbeit von dem System in die Umgebung abgegeben, damit beispiels­weise ein Motor das Auto antreibt.

Wenn man also eine Wärme­menge zuführt, und gleich­zeitig Arbeit verrichtet, erhält man:

In diesem Fall geht die Wärme­menge nur teil­weise in die innere Energie ΔU des Systems über. Denn ein anderer Teil wird in mecha­nische Arbeit abge­führt. In dieser Beziehung ist bereits der Energie­erhaltungs­satz enthalten. Das, was man an Energie der ungeord­neten Molekular­bewegung hineinsteckt, geht zum Teil in die Änderung der inneren Energie und zum Teil in Abführung von mecha­nischer Arbeit in die Umgebung.

Eigent­lich haben wir mit obiger Gleichung schon den ersten Haupt­satz der Wärme­lehre. Dieser Haupt­satz sagt im Grunde nichts anderes aus, als das der Energie­erhaltungs­satz auch bei thermo­dynamischen Systemen Anwen­dung findet. Aber dazu kommen wir noch konkret. Also, die Änderung der inneren Energie hängt mit einer Änderung der Wärme und mit dem Verrichten von mecha­nischer Arbeit zusammen. Nur so kann sich die innere Energie ändern.

Was bedeutet das konkret für obigen Fall?

Der Temperatur­zuwachs ΔT wird jetzt bei konstantem Druck kleiner sein, als bei konstantem Volumen. Denn ein Teil bleibt noch übrig für die Arbeits­verrichtung.

Die verrichtete Arbeit lässt sich daher ausrechnen als:

F   Kraft auf die Kolbenfläche
Δs   ist die Wegstrecke des Kolbens
A   ist die Kolbenfläche

Andererseits gilt folgendes:

F / A   entspricht dem Druck p auf die Kolbenfläche
A · Δs   ist die Änderung des Volumens ΔV

Somit lässt sich die verrichte Arbeit auch wie folgt ausdrücken:

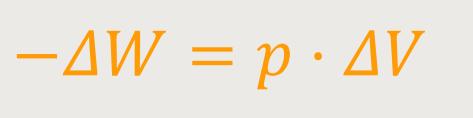
Für die Wärme­menge kann man jetzt, bezogen auf die innere Energie und unter Berück­sichtigung der abge­führten Arbeit, schreiben:

Gleich folgt noch eine kleine Umformung, und schon ist man fast am Ziel. Zunächst erinnern uns, für ein ideales Gas gilt ja:

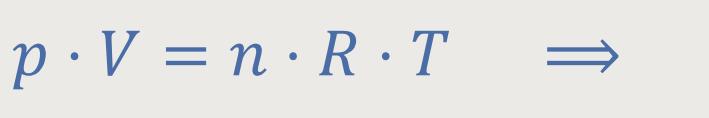
Da der Druck in diesem Fall ein konstanter Faktor ist, wird sich nur das Volumen ändern und entspre­chend auch die Tempe­ratur:

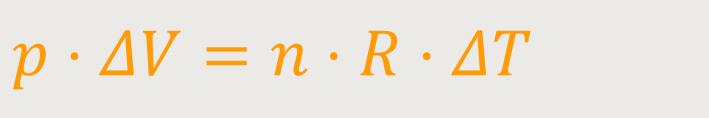
Der Kolben bewegt sich in einem Umfeld, bei dem der Außen­druck und auch der Innen­druck immer in einem Gleich­gewicht bleiben. Wird dieser Ausdruck entspre­chend eingesetzt, erhält man schließ­lich:

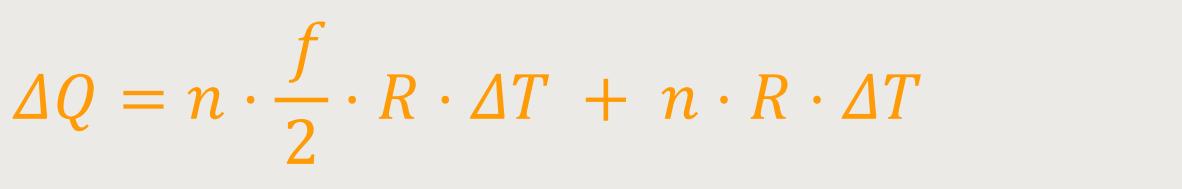
Nach einer weiteren Umformung ergibt sich:

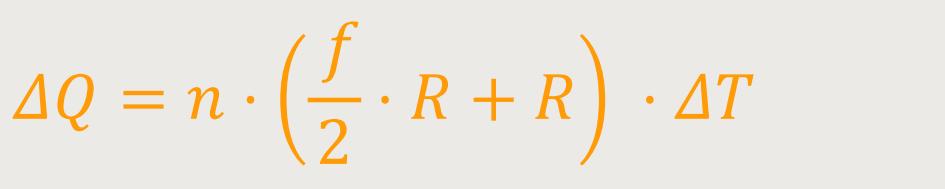
Wenn man das jetzt weiter oben mit der Definition bei konstantem Volumen vergleicht, ergibt sich eine gewisse Ähnlichkeit. Da C_V die Mol­wärme bei konstantem Volumen ist, wird jetzt daraus die Mol­wärme C_p bei konstantem Druck. In der Gleichung ent­spricht also das C_p dem ( f/2 · R + R ). Diese Wärme­kapazität ist jetzt aller­dings größer. Denn als Ergebnis erhalten wir:

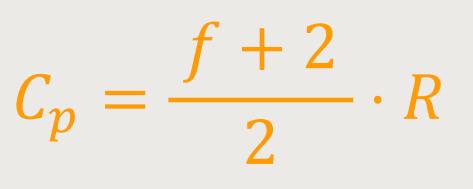
Dieses System hat deshalb eine größere Wärme­kapazi­tät, weil man mehr Wärme zuführen muss, um eine bestimmte Tempe­ratur­änderung zu erreichen. Und warum ist das so? Weil ein Teil der Wärme in mecha­nische Arbeit umgesetzt wird.

Wesentlich ist also, dass bei gleicher zuge­führter Wärme die Tempe­ratur hier weniger stark ansteigt. Und das bedeutet, dass die Wärme­kapazi­tät dieses Systems bei konstantem Druck größer ist. Das System kann demnach mehr Wärme aufnehmen, bis eine bestimmte Tempe­ratur­erhöhung erreicht ist. Außerdem kann sich das System ein bisschen ausdehnen.

Und wenn man das jetzt noch­mals umformt, erhält man für die Gaskonstante, unter Berück­sichtigung eines idealen Gases:

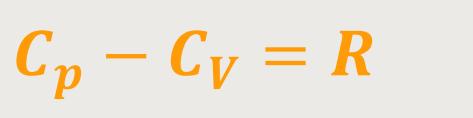
Und letztlich lassen sich beide Größen auch ins Verhältnis setzten:

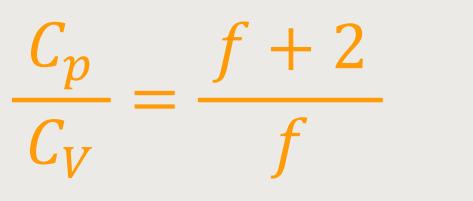
Dadurch erhält man eine Mög­lich­keit, die Anzahl der Frei­heits­grade experi­mentell bestimmen zu können. Dieses Verhältnis wird oft auch als κ (kappa) oder als „Adiabaten-Index” bezeichnet. Darauf kommen wir später noch zu sprechen. Soviel zur Wärmekapazität von Gasen.

Die Flüssig­keiten werden hier wegen ihrer Komplexi­tät nicht näher beleuchtet. Was man dagegen besser beschreiben kann, ist das Verhalten von Fest­körpern. Aber auch dieser Bereich ist sehr komplex. Dennoch werden wir einen wichtigen Fall heraus­greifen.

Für Fest­körper gibt es einen wesent­lichen Unter­schied. In Fest­körpern sausen die Moleküle nicht so wild herum, sondern im Wesent­lichen zittern sie rund um eine Position. Denn wenn sie sich stark herum­bewegen würden, hätten wir ja eine Flüssig­keit, und keinen Fest­körper.

Hierzu kann man sich eine 3-dimen­sionale Gitter­struktur vor­stellen, bestehend aus sehr kleinen Zellen. Und je größer die Tempe­ratur ist, desto stärker zittern die Gitter­atome. Natür­lich erhebt sich die Frage, wer oder was hält sie denn an dem jeweiligen Ort? Die Atome befinden sich in einer Art Potential­mulde und sind im Wesent­lichen lauter kleine harmonische Oszilla­toren. Doch wenn die Tempe­ratur zu hoch wird, werden sie unhar­monisch, und irgend­wann schmilzt der Körper.

Bleibt man dagegen inner­halb gewisser Grenzen, weit weg vom Schmel­zpunkt, haben diese kleinen Oszilla­toren eine kinetische Energie, wenn sie schwingen. Sie haben aber auch eine poten­tielle Energie, wenn sie sich aus ihren Gleich­gewichts­lagen heraus­bewegen. Also zu den Trans­lations­energien, aufgrund der kinetischen Energie dieser Gitter­atome, kommt in gleichem Maße noch eine mittlere poten­tielle Energie hinzu, wenn die Atome aus ihren Gleich­gewichts­lagen wegschwingen.

Das heißt, man hat jetzt nicht nur drei Frei­heits­grade, die mit der Energie gekoppelt sind, sondern drei weitere, bei der die poten­tielle Energie mit eingeht. Das trifft zum Beispiel auf die Gas­moleküle nicht zu, denn dort kommt es nur dann zu einer Wechsel­wirkung, wenn sie zufällig gerade zusammen­stoßen. Und deshalb bedeutet das für die Fest­körper, dass sich die Mol-Wärme C entspre­chend ändert.

Das f besteht jetzt aus 6 Freiheits­graden, und nicht mehr nur aus 3 Freiheits­graden. Die zusätz­lichen Freiheits­grade haben aber nichts mit der Mög­lich­keit der Rotation zu tun, sondern hier kommen zu den Energien, die sich kinetisch auf die drei Trans­lations­richtungen aufteilen, noch einmal so viele für die poten­tiellen Energien hinzu. Und daher erhält man:

Das ist das Dulong-Petitsche Gesetz, welches bei vielen Festkörpern erfüllt ist.

Bei der Thermo­dynamik kann man mit relativ einfachen Mitteln vieles über das Verhalten von Systemen aussagen, ohne im Einzelnen die Struktur und die Wechsel­wirkungen der Moleküle kennen zu müssen.

⇦ Kapitel Kapitel ⇨