Eine wesent­liche weitere Betrachtung ist die berühmte „Wellen­gleichung”. Die Wellen­gleichung ist eine der wichtigsten Differential­gleichungen in der Physik über­haupt. Mit den bisherigen einfachen Überlegungen können wir uns diese Gleichung jetzt anschaulich machen.

In der Elektro­dynamik ergibt sich die Wellen­gleichung aus den Grund­gleichungen, nämlich den Maxwell-Gleichungen. Und daraus konnte der Schluss gezogen werden, dass es elektro­magne­tische Wellen über­haupt gibt, die sich gleich schnell wie das Licht ausbreiten. In ähn­licher Weise lässt sich die Wellen­gleichung auch hier von den Grund­gleichungen ableiten.

Um zu verstehen, wie es zu dieser Wellen­gleichung kommt, und was man darunter versteht, werden wir einiges von dem zugrunde legen, was wir bereits betrachtet haben. Hierzu rufen wir uns nochmals eine harmo­nische Welle in den Sinn zurück, die zwar nur einen Spezial­fall von vielen unter­schied­lichen Wellen dar­stellt, aber dennoch einen ganz wichtigen.

Man verfolgt auch bei der Wellen­gleichung das Ziel, wieder eine Differential­gleichung zu erhalten. Was kommt heraus, wenn man die Auslenkung u, die ja eine Funktion von (x, t) ist, zuerst nach x und dann nach t ableitet?

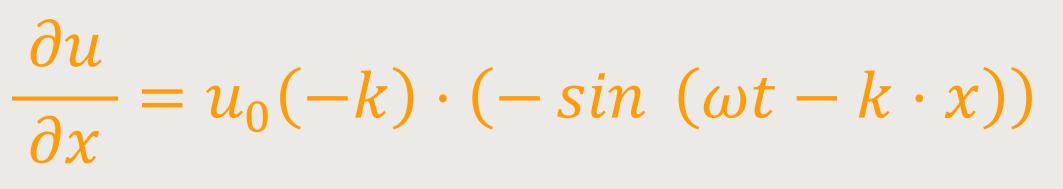
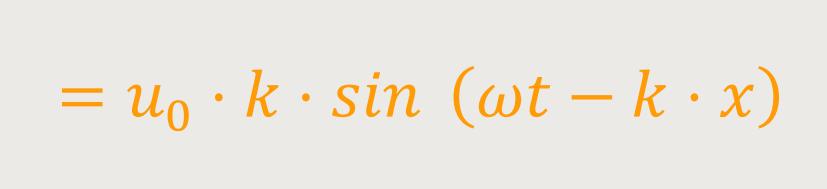
u_₀   ist die zeitunabhängige Amplitude

Hinweis: Wenn man den Sinus differenziert, dann kommt der Kosinus (Cosinus) heraus. Und wenn man den Kosinus differenziert, dann kommt ein minus Sinus heraus.

Jetzt differenziert man noch einmal nach x:

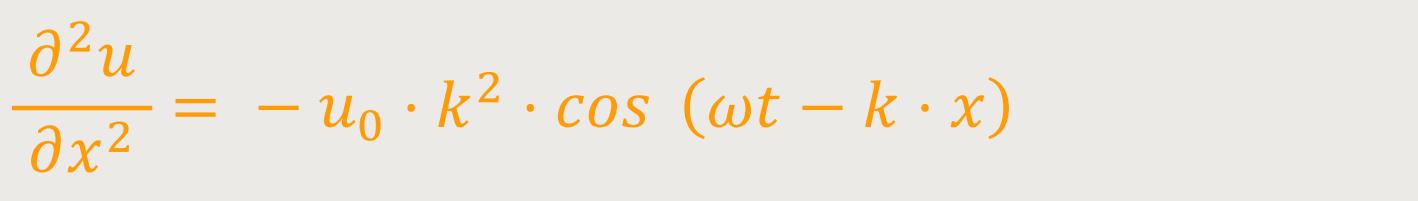
u_₀ · k   ist eine konstante Amplitude

Hier wurde das u  nach  x partiell zweimal abgeleitet. Das heißt, dass t wurde konstant gehalten. Und jetzt macht man genau das gleiche noch einmal, indem man jetzt das u  nach  t zweimal ableitet. Letzten Endes erhält man anlog:

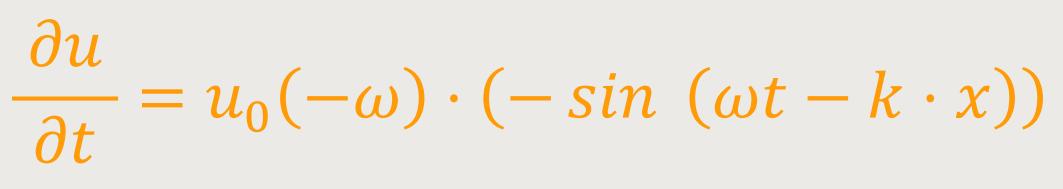
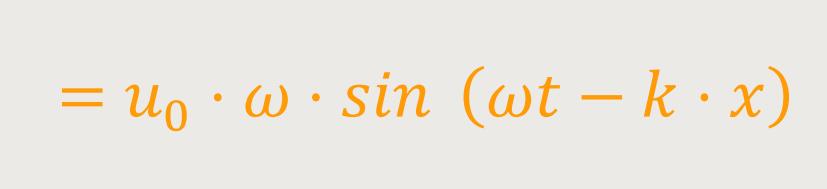
Und hier differenziert man noch einmal nach t:

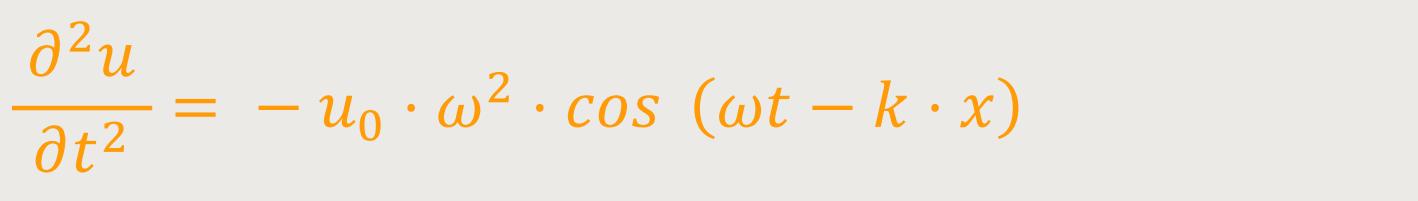
Durch die zweifache Differentiation erhält man zwei Beziehungen, die man nur noch umformen muss.

Wenn man die erste Beziehung umformt, ergibt sich daraus:

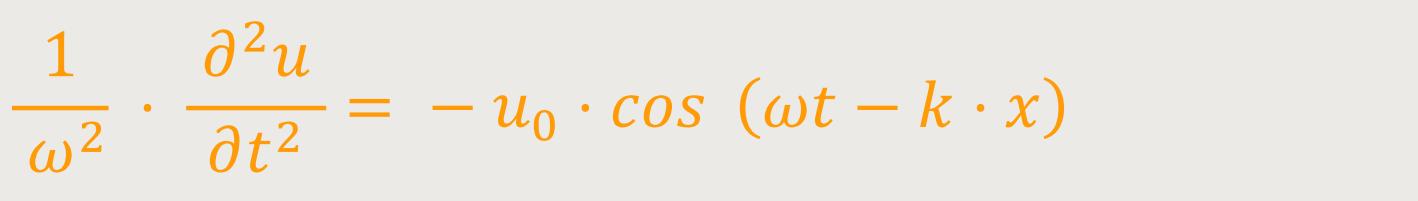
Wenn man die zweite Beziehung umformt, ergibt sich daraus:

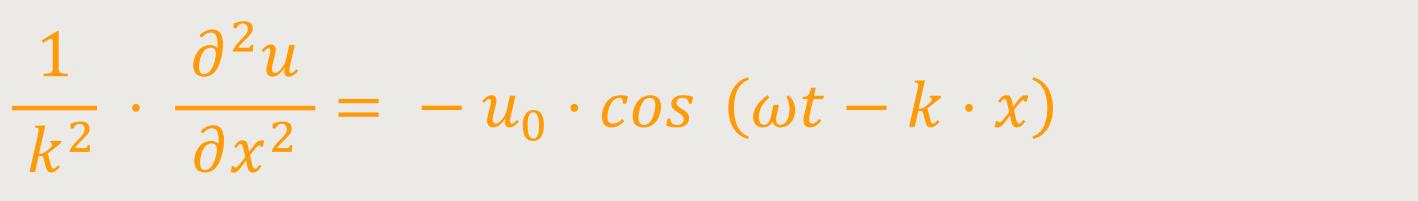
In beiden Fällen bleibt auf einer Seite der Gleichung der gleiche Term übrig, und man kann somit beides Gleichsetzen:

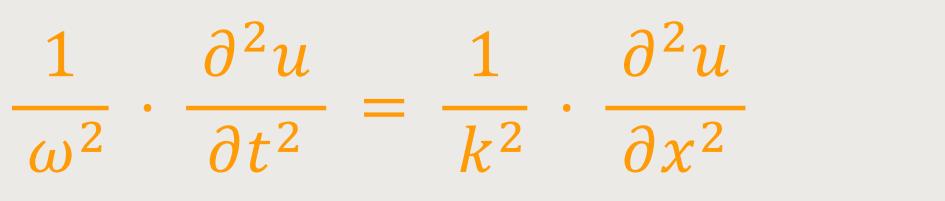
Abschließend formt man noch einmal gering­fügig um, denn wir wissen ja inzwischen, was man unter der Phasen­geschwindig­keit versteht. Man multipliziert also k² auf die andere Seite. Dann erhält man:

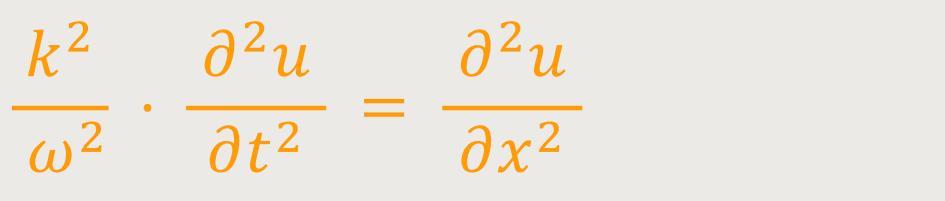
Wenn die Phasen­geschwindig­keit v_ph = ω /k ist, dann ent­spricht 1 /v_ph² = k² /ω², und damit ergibt sich jetzt:

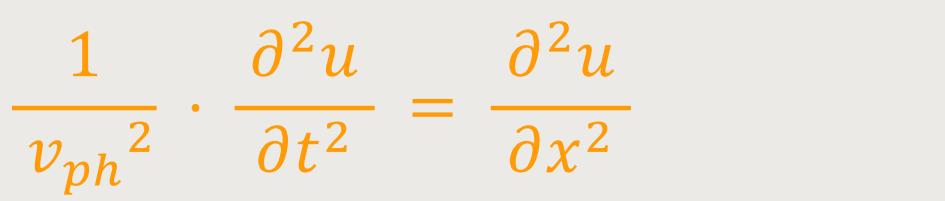
Bei Differential­gleichungen geht man gerne so vor, dass man alle Terme, hier eine Funktion zweier Variablen, auf eine Seite schreibt:

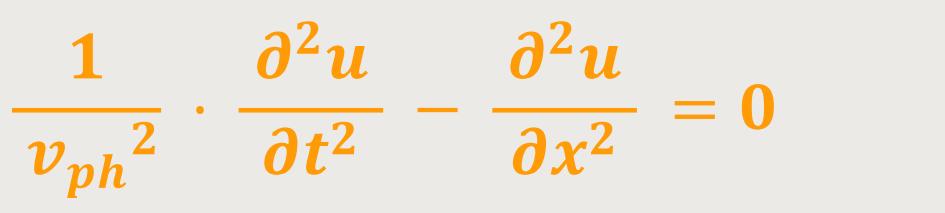
Diese Gleichung ist die 1-dimen­sionale Wellen­gleichung.

Jetzt lässt sich die Wellen­gleichung ganz leicht auch auf drei Dimen­sionen erweitern. Denn wenn man davon ausgeht, dass die Aus­lenkung u auch von der y- und von der z-Koordinate abhängig ist, dann erhält man noch weitere doppelte Ableitungen nach y und nach z.

Dementspre­chend ergibt sich daraus für die 3-dimen­sionale Wellen­gleichung:

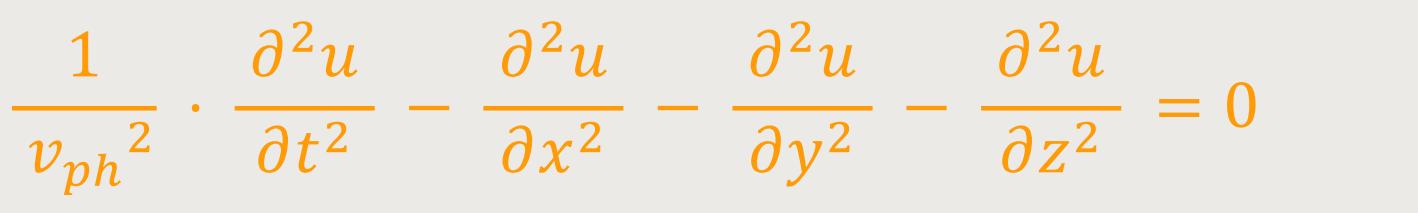
Um das nicht so umständ­lich aufzu­schreiben, verwendet man für 3-dimen­sionale Wellen auch gerne den Ausdruck:

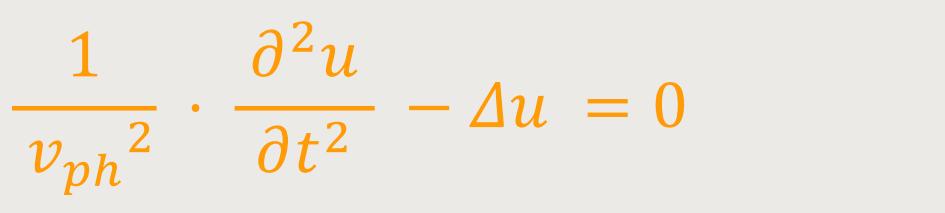
Dieses Delta ist jetzt ein anderes Delta, als das, was wir oft verwendet haben. Es ist nämlich in seiner Dimension kein kleines dimen­sionales Delta, sondern wir definieren es als:

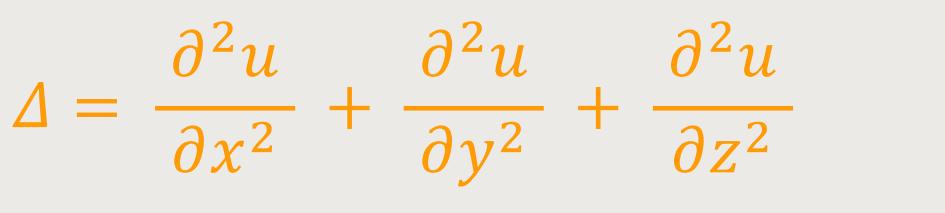
Im Grunde ist das jetzt ein Operator, der angewendet wird auf eine Funktion von (x, y, z). Dieses Δ (Delta) ist der soge­nannte Laplace-Operator. Mit Hilfe dieses Laplace-Operators erhält man hier die 3-dimen­sionale Wellen­gleichung. Wichtig ist, das in dieser Wellen­gleichung die Phasen­geschwindig­keit der Aus­breitung der Welle, um die es jeweils geht, konkret enthalten ist.

Damit ergibt sich also der wesent­liche Ausgangs­punkt dafür, wie man Wellen all­gemein unter­suchen kann. Natür­lich muss zuvor, wie es bei Differential­gleichungen oft der Fall ist, fest­gelegt werden, welche Bedingungen die Lösungen erfüllen müssen. Denn es gibt eine große Viel­zahl unter­schied­licher Lösungen dieser Wellen­gleichung. Daher ist es nicht verwunder­lich, dass es kaum eine Differential­gleichung gibt, die in der Mathe­matik inten­siver unter­sucht wurde, als die Wellen­gleichung.

Daher ist es wichtig zu wissen, wie man Anfangs­wert­probleme und Rand­wert­probleme löst. Wenn man beispiels­weise die 2-dimen­sionale Schwingung eines Schlagzeug-Trommel­fells anschaut. Es ist nämlich nicht unerheblich, an welcher Stelle man auf das Trommel­fell schlägt, und wie das Fell am Rand einge­spannt ist.

Dennoch lässt sich sagen, man versteht unter einer Welle alles, was dieser Wellen­gleichung genügt. Wenn­gleich es weit mehr ist, als nur die Betrach­tung einer ein­fachen harmo­nischen Welle, die hier als Ausgangs­punkt gewählt wurde.

Zwei Dinge ergeben sich aus der Gültig­keit der Wellen­gleichung. Das eine ist ein Prinzip, das schon ein paar hundert Jahre alt ist, nämlich das Huygens-Fresnel-Prinzip. Dieses Prinzip besagt, wenn ein Punkt in einem Wellen­feld von einer Wellen­front getroffen wird, dass dieser Punkt als Ausgangs­punkt einer neuen Kugel­welle auf­gefasst werden kann. Dieses Prinzip macht die Aus­breitung von Wellen etwas nach­voll­ziehbarer.

So kann es zum Beispiel vorkommen, dass eine oder mehrere Wellen­fronten auf eine Anordnung von Punkten treffen. Dass diese Punkte wiederum Ausgangs­punkte von neuen Kugel­wellen sind, lässt sich nach­voll­ziehen. Wenn sich diese Kugel­wellen anschlie­ßend über­lagern, ergibt sich daraus einfach ein Weiter­laufen der Wellen­front. Trifft eine solche Wellen­front im weiteren Verlauf auf eine relativ kleine Öffnung, pflanzt sich die Wellen­front nach der Öffnung in Form einer Kugel­welle fort.

Ein zweites wichtiges Prinzip, das insbe­sondere in der Optik sehr wichtig ist, ist das Fermat-Prinzip. Dieses Prinzip ist zunächst etwas ganz anderes, obwohl es auch aus der Wellen­gleichung folgt. Bildet man die Ableitung, erkennt man, dass es einen ganz ähn­lichen Ursprung hat. Dieses Prinzip wurde für die Licht­wellen formuliert und es sagt aus, dass eine Welle, und insbe­sondere das Licht, zwischen zwei Punkten den Weg wählt, für den es die kürzeste Zeit benötigt.

Das sind zwei wichtige Grund­prinzipen, aus denen fast die gesamte Optik, so wie wir sie heute kennen, letzten Endes her­geleitet werden kann. Diese Grund­lagen, spielen bei der Beschrei­bung von Licht­wellen und optischen Phäno­menen eine wesent­liche Rolle. Wir werden im Bereich der Elektro­dynamik auf diese beiden Prinzipien noch etwas näher eingehen.

⇦ Kapitel Kapitel ⇨