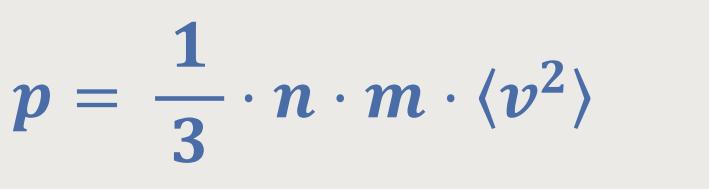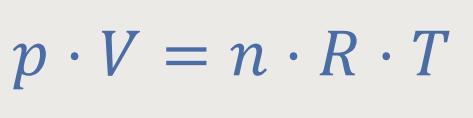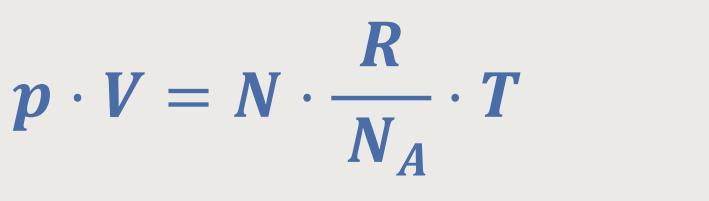Im letzten Kapitel haben wir die berühmte Grund­gleichung von Daniel Bernoulli für die statis­tische Inter­pretation der Bewegung von Gas­molekülen und letzt­lich der Tempe­ratur hergeleitet:

p   ist der Druck auf die Wand des Behälters
n = N /V   ist hier die die Molekülanzahldichte
m   ist die Masse eines Moleküls
⟨ v²⟩   ist das mittlere Geschwindigkeitsquadrat der Moleküle

Mit wenigen weiteren Schritten kann aus dieser Gleichung abge­leitet werden, was physika­lisch unter der Temperatur zu verstehen ist. Bis jetzt wurde die Tempe­ratur nur rein empirisch ermittelt. Hierzu wurde zwischen den jeweiligen Schmelz­punkten entspre­chend inter­poliert. Aber das ist keine wirkliche Definition für eine physika­lische Größe.

Wir erinnern uns, die Zustands­gleichung für ideale Gase lautete:

Und die Molekül­anzahl­dichte war definiert als:

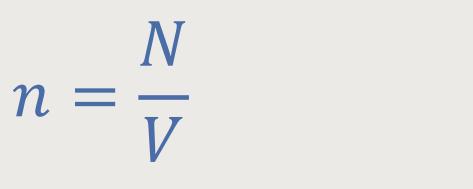
Wenn man jetzt die Bernoulli-Gleichung zunächst einmal mit dem Volumen V erweitert und gleich­zeitig die Molekül­anzahl­dichte berück­sichtigt ergibt sich:

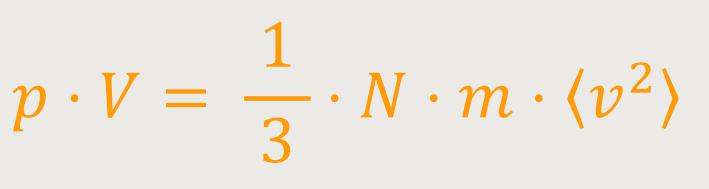
Außerdem wissen wir, dass die kinetische Energie eines Moleküls (m · v²) /2 ent­spricht. Also erweitern wir die Gleichung einfach:

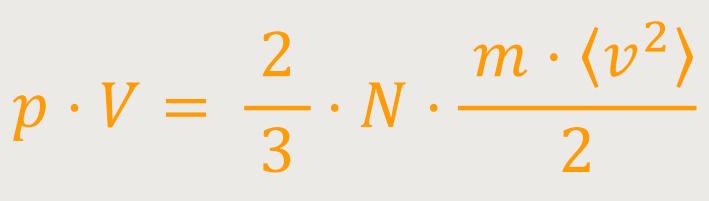
Auf diese Weise erhalten wir als Faktor den Mittelwert der kinetischen Energie von einem Molekül. Natür­lich kann ein solches Molekül auch Rotationen und innere Schwingungen voll­ziehen. Dadurch wird dem Molekül weitere kinetische Energie zugeführt. Und zwar kinetische Energie der Rotation und kinetische Energie der Schwingungen. Wir hatten jedoch voraus­gesetzt, dass es sich nur um punkt­förmige Teil­chen handeln soll, die sich vorerst nur trans­latorisch fort­bewegen. In diesem Fall steht der Ausdruck (m · v²) /2 für die gesamte mittlere Energie ⟨ E_Kin⟩. Würden all­gemeinere Bedingungen vorliegen, müsste das natürlich entspre­chend berück­sichtigt werden. Und damit ergibt sich als Folgerung:

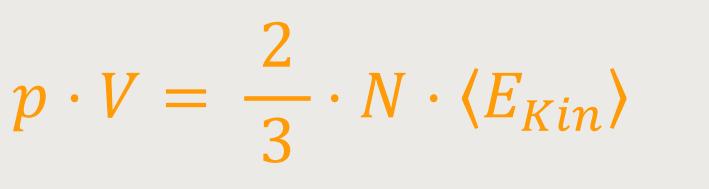
Daraus erkennt man schon, dass die mittlere kinetische Energie eines Moleküls propor­tional zur Temperatur des Körpers ist:

Und jetzt macht man einen entspre­chenden Ansatz, um beides mit­einander in Relation zu bringen:

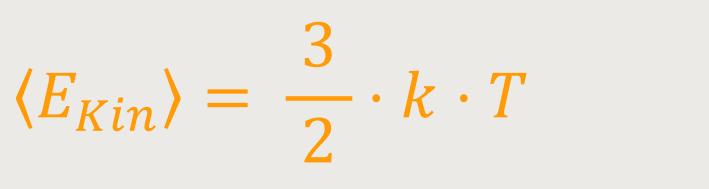
k   ist der Proportionalitäts­faktor

Dieser Propor­tionalitäts­faktor ist die bereits ange­sprochene Boltzmann-Konstante. Oft wird diese in der Literatur mit k_B wieder­gegeben.

Die Tempe­ratur ist demnach ein Maß für die mittlere kinetische Energie eines Moleküls in dem Gas. Egal, ob man viele Moleküle zu einem Zeit­punkt anschaut, oder einzelne Moleküle längere Zeit verfolgt. Im Mittel kommt immer diese mittlere kinetische Energie heraus. Und wenn man das jetzt einsetzt, erhält man:

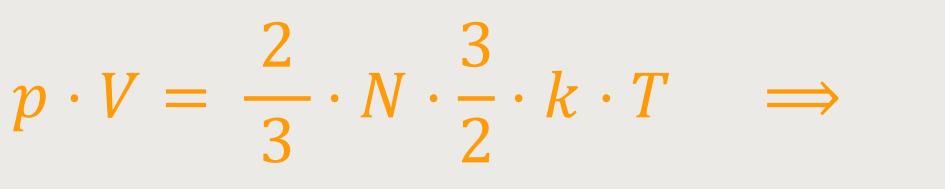
Auch hier erhalten wir die Zustandsgleichung idealer Gase.

Jetzt kann man diese Zustandsgleichung mit der Zustandsgleichung vergleichen, die wir bereits ein paar Kapitel zuvor experimentell definiert hatten:

Daraus folgt jetzt, das k = R/N_A entspricht.

R   ist die allgemeine Gaskonstante
N_A   ist die Anzahl der Moleküle in 1 kmol

Aufgrund von Unter­suchungen der Brownschen Bewegung, lässt sich ermitteln, wie stark sich so ein Teil­chen über längere Zeit von einem Ausgangs­punkt in eine bestimmte Richtung weg­bewegt. Und wenn man diese Bewegungen mittelt, lässt sich die Boltzmann-Konstante direkt fest­stellen.

Das R erhält man unmittel­bar aus den quanti­tativen Unter­suchungen der Zustands­gleichung idealer Gase. Und wenn man wiederum den Propor­tionalitäts­faktor k und die Gas­konstante R kennt, lässt sich ohne weiteres auch das N_A bestimmen:

Warum ist der Propor­tionalitäts­faktor k so winzig? Weil es hier um die mittlere kinetische Energie nur eines einzelnen Moleküls geht. All das gilt nach wie vor für den sehr speziellen Fall eines idealen Gases, mit den entspre­chenden Ein­schrän­kungen, die wir zuvor fest­gelegt hatten. Wir haben bisher nur drei Trans­lations-Freiheits­grade und damit nur die kinetische Trans­lations­energie zuge­lassen.

An dieser Stelle kann man eine erste Verall­gemeine­rung machen, um den Tempe­ratur­begriff zu erweitern. Schließ­lich möchte man ihn ja auf verschie­dene weitere Systeme anwenden. Und daher gilt, bezogen auf den zuvor gemachten Ansatz, für die mittlere kinetische Energie pro Freiheits­grad:

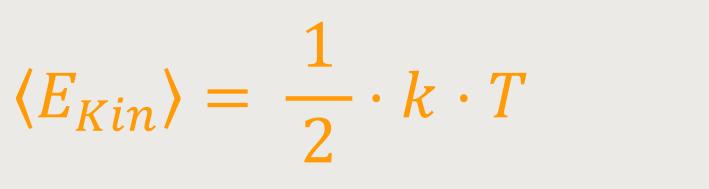
Im Allge­meinen kann man davon aus­gehen, dass sich die Energien auf alle Frei­heits­grade gleicher­maßen auf­teilen werden. Und damit ergibt sich eine Verall­gemeine­rung. Wenn wir Moleküle betrachten, die f Freiheits­grade haben, dann gilt:

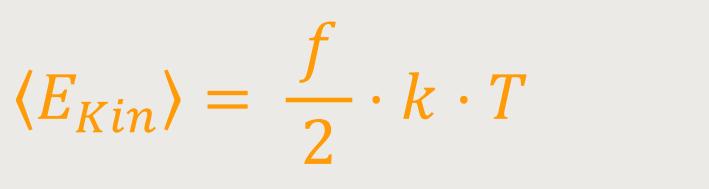
Damit sind schon deut­lich allge­meinere Systeme zugelassen, bei denen eine höhere Anzahl von Frei­heits­graden vor­liegen kann. Bei größeren Molekülen kommen noch Rotations­mög­lich­keiten hinzu. Aller­dings kann es sein, dass aufgrund quanten­mecha­nischer Einschrän­kungen nicht alle Frei­heits­grade aktiviert werden können, und deshalb viel­leicht nur zwei Rotations-Freiheits­grade ver­bleiben.

Bei sehr hohen Tempe­raturen können die Moleküle zusätz­lich im Innern zum Schwingen gebracht werden, wodurch ein zusätz­licher Frei­heits­grad auftritt. All das muss berück­sichtigt werden. Aber ansonsten ist der Begriff der absoluten Tempe­ratur unmittelbar verbunden mit dem Begriff der mittleren kinetischen Energie eines Moleküls des entspre­chenden Körpers.

Nach wie vor muss unter­schieden werden zwischen der Tempe­ratur und der Wärme­menge. Bei der Betrach­tung der Wärme­menge hatten wir bereits gesehen, dass man diese letzt­lich als eine Energie­form auf­fassen kann. Es ging dabei um die gesamte kinetische Energie aller Moleküle in einem entspre­chenden System. Und wenn die Masse größer ist, dann wird auch die Wärme­menge ansteigen, weil sich mehr Moleküle im System befinden.

Bei unserer Betrach­tung geht es aller­dings immer um die mittlere kinetische Energie eines Moleküls. Und selbst wenn man einen größeren Topf mit Wasser erhitzt, wird die mittlere kinetische Energie jedes einzelnen Moleküls gleich bleiben. Also, die Tempe­ratur ist eine intensive Größe, die von der Masse des Körpers unab­hängig ist, während die Wärme­menge die Summe aller kinetischen Energien beinhaltet. Und wenn halt mehr Moleküle vorhanden sind, dann ist auch die Summe der Energien entspre­chend größer.

Jetzt machen wir noch eine zweite Verall­gemeinerung, um das Thema zu erweitern und zu erläutern, was man generell unter der Tempe­ratur versteht. Diese zweite Verall­gemeinerung beinhaltet, dass wir die Definition mit f Frei­heits­graden nicht nur bei idealen Gasen anwenden, sondern auch auf Körper über­tragen.

Verständlicher Weise ist das viel komplizierter zu berechnen, weil die Moleküle unter­einander auch Wechsel­wirkungen haben. Und dann kommen noch poten­tielle Energien hinzu. Letzt­lich muss man sogar davon ausgehen, dass es zu Fluktua­tionen, also Schwan­kungen im System kommt. Denn die Moleküle werden nicht immer die gleiche kinetische Energie haben. Und so ergibt sich die Frage, wie sich die kinetische Energie oder ins­besondere die Geschwin­dig­keiten der Moleküle in einem Gas verteilen? Also, wie viele Moleküle haben die eine Geschwin­dig­keit, wie viele Moleküle haben eine andere Geschwin­dig­keit? Und wie groß ist die anteilige Verteilung dieser Geschwin­dig­keiten? Diesbezüg­lich gibt es verschiedene Arten der Darstellung.

Nachfolgend sprechen wir kurz über die Fluktua­tionen und damit über die Verteilung der Geschwindig­keiten.

Der Ausgangs­punkt der Betrach­tung ist wieder das ideale Gas, weil es eine Sonder­stellung ein­nimmt und besonders ein­fach zu beschreiben ist. Denn durch die Wechsel­wirkungs­kräfte, die in den Körpern auf­treten, sei es in den Flüssig­keiten, und noch mehr bei den Fest­körpern, wird die Berechnung viel aufwendiger.

Wir gehen jetzt von einem idealen Gas mit der Temperatur T aus. Des Weiteren setzen wir hier voraus, dass sich dieses ideale Gas in einem homogenen Gravita­tions­feld befindet beispiels­weise hier auf der Erdober­fläche, mit einer Feld­stärke g. Außerdem wissen wir bereits von der barometrischen Höhenformel, dass sich der Druck in Abhängigkeit von der Höhe bzw. der z-Koordinate ändern wird. Man definiert diesen Druck als:

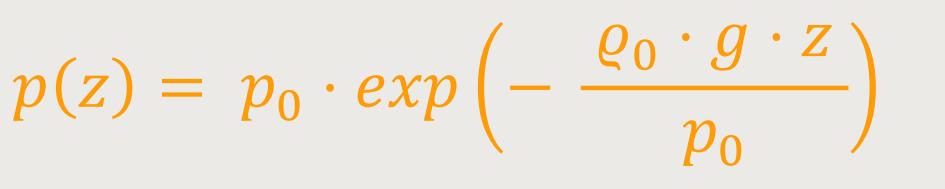
Das ist barometrische Höhenformel.

p_₀   ist der Gasdruck auf einem Referenzniveau Null
ϱ_₀  ist die Dichte des Gases pro Volumeneinheit bei Referenzniveau
g   ist die Fallbeschleunigung
z   ist die senkrechte Höhenkoordinate

Jetzt werden wir die barometrische Höhen­formel umformen. Unter Berück­sichtigung der Zustands­gleichung idealer Gase ergibt sich zunächst:

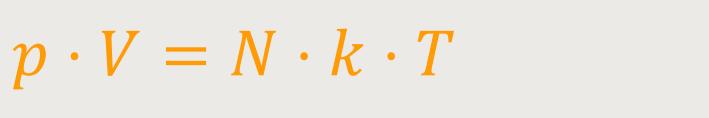
Da die Molekül­anzahl­dichte definiert war als n = N/V, erhält man durch Umformen und Einsetzen:

Und wenn ϱ = n · m entspricht, dann erhält man noch­mals durch Umformen und Einsetzen:

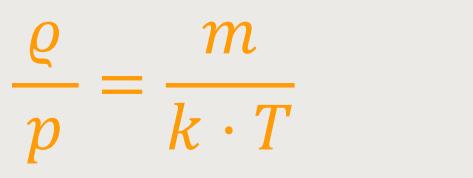
Bei einer bestimmten Tempe­ratur ist das ϱ/p für das ideale Gas immer dasselbe, solange man die konstante Molekül­masse und die Boltzmann-Konstante hat.

Wenn man jetzt die durch Umformung erhaltene Beziehung, in die barome­trische Höhen­formel ein­setzt, ergibt sich daraus als Folgerung:

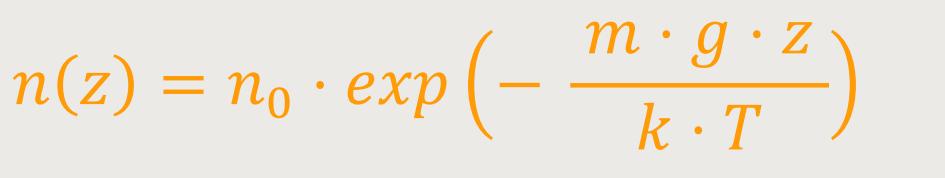
Bei aufmerksamer Betrachtung erkennt man, dass dieses m · g · z offen­sicht­lich der poten­tiellen Energie eines Moleküls mit der Masse m entspricht, wenn es sich in der Höhe z über Boden­niveau befindet. Das Minus im Term ist not­wendig, weil die Dichte nach oben hin immer kleiner wird.

Jetzt folgt noch der Zusammen­hang mit der Geschwin­dig­keits­verteilung. Hierzu stellen wir folgende gedank­liche Überlegung an:

In einem säulen­förmigen System ist die Molekül­anzahl­dichte je nach Höhe unter­schiedlich. Man kann annehmen, dass die Moleküle in der Höhe z = 0 eine derartige kinetische Energie haben, die es ihnen gerade ermöglicht, auf die Höhe m · g · z aufzu­steigen, bevor sie wieder runter­fallen. Und nachdem die Moleküle unter­schied­lich hoch auf­steigen, gibt es entspre­chend für den unteren Bereich eine Verteilung dieser Geschwin­dig­keits­beträge.

Das heißt, die kinetische Energie entspricht bei der jeweiligen Temperatur:

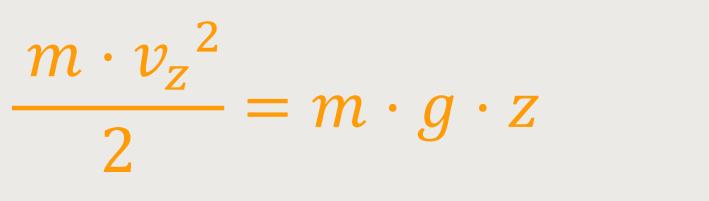
Wobei m · g · z die potentielle Energie ist, die auf­gebracht werden muss, um dieses Molekül aus der Höhe z = 0 auf diese Höhe z hinauf­zuheben.

Mittels der barome­trischen Höhen­formel hat man jetzt die Mög­lich­keit, eine Geschwin­dig­keits­verteilung in der Höhe z = 0 anzugeben. Interessant ist zunächst der Zustand auf dem Bodenniveau. Diese Geschwin­dig­keits­verteilung ist dann:

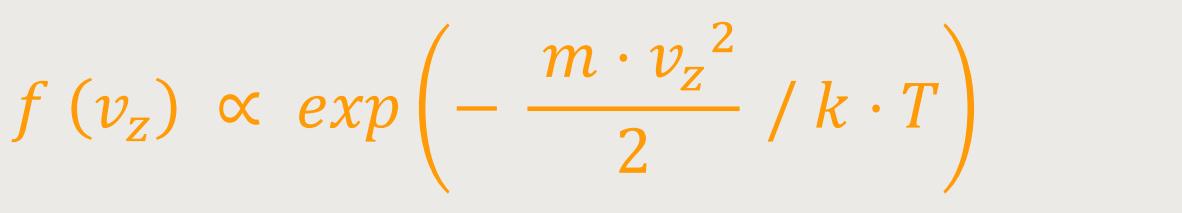
Wie lässt sich jetzt diese Verteilungs­funktion inter­pretieren?

Im Grunde geht es darum, dass man sich aus einer solchen Verteilungs­funktion eine Wahr­schein­lich­keit ableitet. Wie groß nämlich die Wahr­schein­lich­keit ist, dass ein Molekül eine bestimmte z-Komponente der Geschwin­dig­keit hat. Und dieses f (z) fasst man als eine Wahr­schein­lich­keits­dichte auf. Es geht letzt­lich um die Wahr­schein­lich­keit, dass die z-Komponente der Geschwin­dig­keit ∈ [v_z, v_z+dv_z] ist. Man schreibt daher:

Dazu muss man immer ein gewisses Inter­vall zulassen, in welchem die Geschwin­dig­keit liegen soll. Je breiter das Intervall ist, desto breiter wird auch die Wahr­schein­lich­keit sein. Man sagt deshalb auch:

f (v_z) ist die Wahrschein­lichkeitsdichte

Hinweis: Wenn man sich später mit der Quanten­mechanik beschäftigt, wird dort die Aufenthalts­wahr­schein­lich­keit von Teil­chen, beispiels­weise von Elek­tronen in der Elek­tronen­hülle eines Atoms ebenso mit einer Wahr­schein­lich­keits­dichte-Funktion ange­geben. Dort geht es dann um die wirk­lichen Wahr­schein­lich­keiten, dass sich dieses Elektron in einem bestimmten Volumen­element dv befindet. Es lässt sich dann ausrechnen als Wahr­schein­lich­keits­dichte multi­pliziert mit der Größe dieses Volumen­elements dv.

Daraus ergibt sich eine wichtige Folgerung:

Wenn dieses f (v_z) konkret eine Wahr­schein­lich­keits­dichte ist, dann heißt das, wenn man über alle möglichen v_z von minus unendlich bis plus unendlich aufintegriert, muss 1 herauskommen. Denn irgen­deine Geschwin­dig­keit muss das Molekül ja haben. Und durch Normierung auf 1 kann man obiger Größe noch einen entspre­chenden Vor­faktor ver­schaffen. Hierzu bildet man das Integral von f (v_z) · dv_z. Letzt­lich erhält man folgende Beziehung::

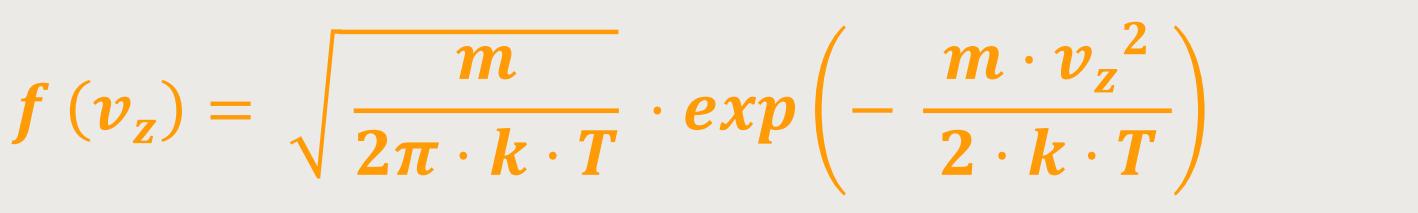
Das ist die normierte Wahr­schein­lich­keits­dichte für das Auf­treten der z-Komponente der Geschwindigkeit.

Bisher haben wir das nur für eine Geschwin­dig­keits­komponente betrachtet. In vielen Fällen ist es aber so, dass man in einem Gas ein isotropes System vorfindet. Die Moleküle haben dann in allen drei Raum­rich­tungen eine entspre­chende Wahr­schein­lich­keits­dichte. Also, wenn man daher eine solche Isotropie annimmt, kann man eine relativ ein­fache Verall­gemeinerung machen.

Hierzu betrachtet man nicht nur ein f von einer einzelnen Komponente, sondern von dem gesamten Geschwin­dig­keits­vektor, mit einer v_x-, einer v_y- und einer v_z-Kompo­nente. Auch das muss entspre­chend wieder normiert werden:

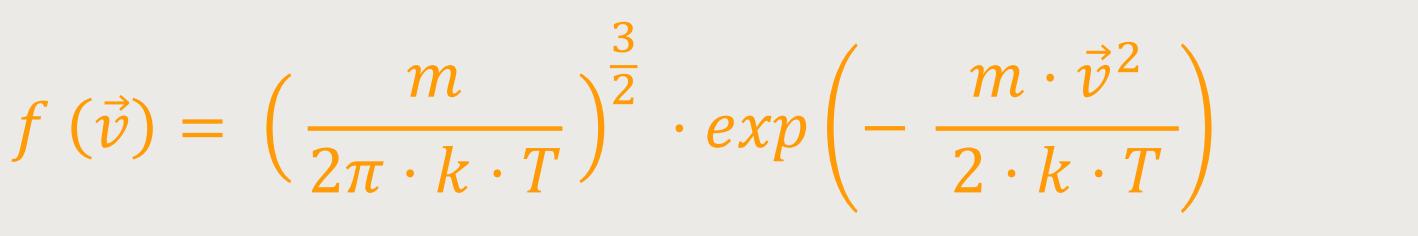
f () · dv_x · dv_y · dv_z ist jetzt die Wahr­schein­lich­keit, dass:

die x-Komponente ∈ [v_x , v_x+dv_x] und
die y-Komponente ∈ [v_y , v_y+dv_y] und
die z-Komponente ∈ [v_z , v_z+dv_z] ist.

Und dann erhält man wieder eine symmetrische Verteilung

Grafik (wird später eingefügt)

⇦ Kapitel Kapitel ⇨