• ⇨ Allgemein
• ⇨ Ideale Gase

Was wird eigent­lich physika­lisch mit dem Parameter Tempe­ratur beschrieben? Bei diesen Über­legungen spielen die Gase, und insbe­sondere die idealen Gase, eine Sonder­rolle. Die Gase haben näm­lich die Eigen­schaft, dass die Wechsel­wirkungen der Gas­moleküle praktisch vernach­lässig­bar sind. Es kommt bei Gasen nur dann zu einer Wechsel­wirkung, wenn zwei Moleküle mit­einander kollidieren.

Ihre Temperatur­abhängig­keit ist besonders anschau­lich und einfach zu beschreiben. Deswegen lässt sich auf­grund dieser Abhängig­keit auch die Tempe­ratur sehr genau bestimmen. Es gibt zwei Gesetz­mäßig­keiten, die man in diesem Fall für die idealen Gase gefunden hat. Diese Gesetz­mäßig­keiten führen zur soge­nannten „Zustands­gleichung idealer Gase”.

Unter „idealen Gasen” versteht man zunächst einmal hin­reichend verdünnte Gase. Zur weiteren Beschreibung idealer Gase eignen sich Edel­gase, auch Stick­stoff oder Luft. In diesem Zusammen­hang gibt es zwei experi­mentelle Befunde.

Um das zu veranschau­lichen ver­wendet man ein System, genauer gesagt einen zylinder­för­migen Körper, in welchem ein Kolben bewegt werden kann, ähnlich wie bei einer Luft­pumpe. In einer solchen Druck­kammer befindet sich das Gas, welches unter­sucht werden soll. Und dieses Gas hat einen bestimmten Druck, den man mit einem Druck­manometer messen kann. Wenn man den Durch­messer dieses Zylinders und auch den Hub des Kolbens kennt, lässt sich das Volumen der Kammer berechnen.

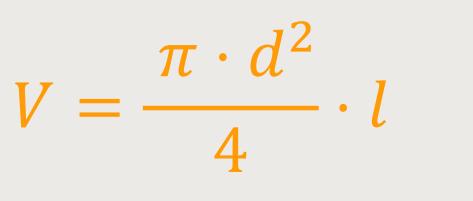
Besonders hilf­reich ist es, wenn man den Hub eines solchen Kolbens auf einer graduierten Skala ablesen kann. Auf diese Weise lässt sich beobachten, wie sich der Druck ändert, wenn das Volumen ver­ändert wird. Was wird zum Beispiel mit dem Druck passieren, wenn man Luft im Kolben, bei einem atmosphä­rischen Druck von 1 bar, auf die Hälfte des Volumens komprimiert?

Im Experiment zeigt sich, dass der Druck bei Halbierung des Volumens auf das Doppelte ansteigt. Was bedeutet das?

Wenn man das Produkt aus den Größen Druck · Volumen betrachtet, und man einerseits das Volumen halbiert, wobei sich gleich­zeitig der Druck verdoppelt, dann ergibt sich daraus, dass das Produkt konstant bleibt:

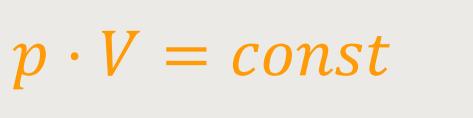
Diese Aussage ist das berühmte Boyle-Mariottesche-Gesetz.

Hierbei ist aller­dings zu berück­sichtigen, dass obiges Experiment bei konstanter Raum­temperatur durch­geführt wurde. Wenn die Kompression langsam genug von­statten geht, findet immer ein Austausch mit der umgebenden Tempe­ratur statt. Man hat im Wesent­lichen während des ganzen Vorgangs ständig Gleich­gewichts­zustände durch­laufen.

Wir erinnern uns, der Parameter der Tempe­ratur wird dadurch charakte­risiert, dass wenn man eine Zeit lang wartet, um ein thermo­dynamisches Gleich­gewicht herzu­stellen, man schließlich fest­stellt, dass zwei in Kontakt befind­liche Körper auf der gleichen Tempe­ratur sein werden. Ein solches Durch­laufen einer Serie von Gleich­gewichts­zuständen, nennt man generell in der Thermo­dynamik einen „quasi statischen” Vorgang, der jeder­zeit reversibel ist.

Das gilt aller­dings nur für ideale Gase. Das Medium Gas ist nicht immer und unter allen Umständen ideal, sondern nur in gewissen Bereichen. Denn wenn das Gas zu sehr kompri­miert wird, kommt man in die Nähe eines Phasen­übergangs. Dann beginnt das Gas zu konden­sieren, und man hat nicht mehr diese ein­fachen Voraus­setzungen. Für unsere Betrach­tung befinden wir uns weit genug weg von irgend­welchen Phasen­über­gängen. Wenn sich also ein Gas wie dieses Boyle-Mariotte-Gesetz verhält, dann nennt man es ein ideales Gas.

Wenn p · V = const, dann ent­spricht die Gleichung einer Hyperbel.

Aber noch spannender wird es für die zweite Gesetz­mäßig­keit. Was wird passieren, wenn man das Experiment jetzt bei unter­schied­lichen Tempe­raturen macht? Nun, das Ergebnis ist relativ einfach. Wenn man die Tempe­ratur erhöht, wird sich einfach nur die Konstante ändern. In einem Diagramm wird die Hyperbel, entspre­chend der konstanten Temperatur­unter­schiede, versetzt ange­ordnet sein. Daher nennt man eine solche Kurve eine „Isotherme”, weil die Temperatur konstant bleibt. Aus diesem Grund werden solche Experi­mente auch langsam durch­geführt. Denn wenn man zu schnell komprimiert, wird das Gas erhitzt, und wenn man zu schnell expandiert, kühlt das Gas ab.

Um zu veranschau­lichen, was bei verschie­denen Tempe­raturen passiert, verwendet man wieder ein System eines zylinder­förmigen Körpers, in welchem ein leicht beweglicher Kolben vor­handen ist. In der Druck­kammer ist nach wie vor das Gas, welches man unter­suchen möchte. Und dieses Gas hat jetzt eine bestimmte Tempe­ratur, die mit einem Tempe­ratur­sensor gemessen wird. Das Gas­volumen bleibt ständig unter konstantem Druck. Auch hier lässt der Abstand des Kolbens auf einer graduierten Skala ablesen. Nun wird das System auf­geheizt, wobei sich der Kolben ohne Ein­wirkung von außen reibungs­frei bewegen kann. Was passiert mit dem Kolben, wenn zum Beispiel Luft, bei einem atmosphä­rischen Druck von 1 bar, in der Druck­kammer erhitzt wird?

Im Experiment zeigt sich, dass sich der Kolben bei konstantem Druck, aber einer Erhöhung der Tempe­ratur so bewegt, dass sich das Volumen linear ausdehnt. Über­trägt man die Volumina und die entspre­chenden Temperaturen in ein V-t-Diagramm, so erhält man eine lineare Funktion. Die Funktion zeigt an, je höher die Tempe­ratur, desto höher das Volumen. Die Gerade wird dementspre­chend die Temperatur­achse unter einem bestimmten Winkel bei ca. −270 °C kreuzen. Was bedeutet das?

Bei ca. −270 °C wäre das Volumen quasi Null. Aber wo ist das Gas? Um diese Frage zu beant­worten stellen wir eine Über­legung an. Grund­sätz­lich hat das Gas ja einen gewissen Druck, der auf seine Umgebung wirkt, in diesem Fall auf den zylin­drischen Körper. Das liegt daran, dass die Gas­moleküle gegen die Wände trommeln und dort einen Impuls­austausch durch­führen. Es werden somit Kräfte aus­geübt, die sich im Druck wider­spiegeln. Erhöht man die Temperatur, erhöht sich somit der Druck. Wenn man dagegen mit der Tempe­ratur immer weiter zurück­geht, dann kann man im Umkehr­schluss davon ausgehen, dass die Moleküle immer träger werden.

Und geht die Tempe­ratur runter, in Richtung immer kleinere Volumina, gelangt man schließ­lich an einen Punkt, an dem das Ende erreicht ist. Man ist dann am Ende angelangt, wenn sich die Gas­moleküle gar nicht mehr bewegen. Sie liegen sprich­wört­lich nur noch herum. Und da die Moleküle ein sehr viel kleineres Eigen­volumen haben, als die Volumina im Experiment, kann man das praktisch vernach­lässigen. Irgend­wann wird die Situation natür­lich grenz­wertig, weil ab einem bestimmten Zeit­punkt flüssige Luft entsteht. Wir gehen aber nach wie vor davon aus, dass es weitest­gehend ein ideales Gas bleibt.

Würde man jedoch Helium statt Luft verwenden, könnte man eine noch tiefere Tempe­ratur erreichen, bis es letzt­lich zu einer Konden­sation kommt.

Wenn man das sehr genau inter­poliert, kommt man letztlich auf eine Tempe­ratur von −273,15 °C. Und das ist jetzt der entschei­dende Punkt. Auf­grund obigen Experi­ments kann man erkennen, dass die Tempe­ratur­skala nach unten hin nicht offen ist. Weniger als ein Null-Volumen gibt es nicht. Eine Tempe­ratur unter­halb dieser Grenz­tempe­ratur wird nicht auf­treten. Bei einem bestimmten Tempe­ratur­wert kommt das System in einen Zustand, wo es nicht mehr weiter geht. Diesen Punkt nennt man den „absoluten Nullpunkt”.

Gerade bei der Beschrei­bung moleku­larer Modelle ist es hilf­reich sich gedank­lich vorzu­stellen, wie beispiels­weise Gas­moleküle in einem System ungeordnet herum­fliegen. Und man kann gut nach­voll­ziehen, dass die Tempe­ratur eine Rolle dabei spielt, wie hektisch sich die Moleküle bewegen. Aber letzten Endes geht es hierbei um die kinetische Energie der Moleküle. Und wenn die Tempe­ratur in dem System nach und nach sinkt, wird auch die kinetische Energie weniger und weniger. Mehr als gar keine kinetische Energie kann man logischer­weise nicht erreichen, denn die kinetische Energie ist positiv definiert. Für obigen experimen­tellen Befund erhält man wieder eine Gleichung. Und da es hierbei eine lineare Beziehung gibt, erhält man:

Diese Gleichung wird auch als Gay-Lussac-Gesetz bezeichnet.

Dieses Gesetz gilt jedoch nur bei p = const, weil ein linearer Zusammen­hang besteht. Die Tempe­ratur wird nur durch konstante und lineare Terme beschrieben.

γ_V   ist ein Vorfaktor mit einem bestimmten Wert
t_C   ist die Temperatur in °C

Und wenn man das t_C gleich 0 °C setzt, dann ergibt sich:

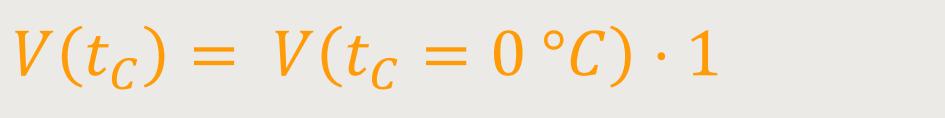
In diesem Fall kreuzt die Gerade als lineare Funktion die Volumen-Achse bei 0 °C. Die Größe bzw. der Winkel des Anstiegs lässt sich experi­mentell ermitteln. Doch was ist, wenn das t_C negative Werte annimmt, wann wird das Volumen V = 0 ? Um das zu erreichen, muss der letzte Term −1 sein, also:

Damit ergibt sich:

γ_V   ist der Volumen-Spannungs­koeffizient

Doch wie sieht die Situation aus, wenn das Medium aus einem anderen Gas besteht? Man könnte annehmen, die Steigung der linearen Funktion verläuft dann flacher oder steiler. Doch da gibt es jetzt einen erstaun­lichen Umstand. Es ist näm­lich egal, welches ideale Gas man verwendet. Solange man einen linearen Zusammen­hang hat, liegt der absolute Null­punkt immer bei −273,15 °C. Das ist quasi etwas Univer­selles. Und damit erhält man für den Volumen-Spannungs­koeffizienten γ_V immer den gleichen Wert.

Es lässt sich im Gegenzug natür­lich auch die andere Beziehung für den Druck aufzeigen:

In diesem Fall ist γ_p = γ_V, aller­dings unter Berück­sichti­gung der experi­mentellen Unsicher­heit. Das ist die gleiche Bezie­hung wie oben, und gilt in diesem Fall nur bei V = const.

An dieser Stelle kann man eine Über­legung anstellen. Wenn man mit der Tempe­ratur nicht tiefer als diesen absoluten Null­punkt kommt, dann könnte man doch einfach die Skala ver­schieben. Eine Tempe­ratur­änderung von 1 °C bleibt weiter­hin eine Tempe­ratur­änderung von 1 °C. Das einzige was man ändert ist, dass man jetzt auf eine absolute Tempe­ratur­skala über­geht, indem man einfach definiert:

T   ist die absolute Temperatur [Kelvin]

Welchen Vorteil hat diese Definition? Wenn die absolute Tempe­ratur bei −273,15 °C liegt, lässt sich das einfach in obige Gleichung ein­setzten, und man erhält damit:

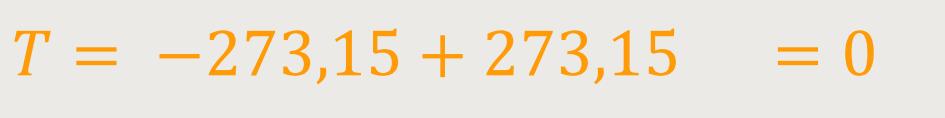
Mit anderen Worten, an dem Punkt, an dem die Moleküle quasi nur noch herum­liegen und keine kinetische Energie mehr haben, liegt jetzt die Temperatur Null. Das ist im Grunde nur eine rationale Über­legung. Die Tempe­ratur­differenzen sind nach wie vor vor­handen, aber man hat die Skala ver­schoben. Sodass der (absolute) Null­punkt jetzt bei −273,15 °C = 0 Kelvin liegt.

Im Nach­folgenden werden wir diese Definition ver­wenden, um damit die Zustands­gleichung für ideale Gase abzu­leiten. Im Umkehr­schluss werden wir berück­sichtigen, wenn sich ein Gas so verhält, dass es dieser Gleichung genügt, dann ist es ein ideales Gas. Und wenn es sich nicht so verhält, befinden wir uns in der Nähe von Phasen­über­gängen.

Jetzt formen wir die obige Gleichung ...

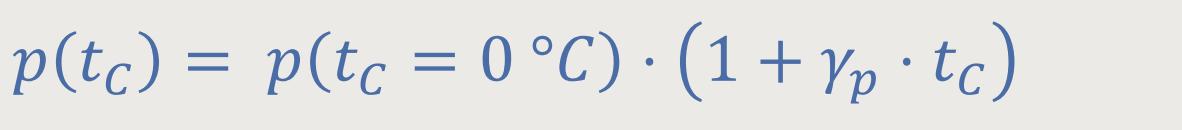
... um, indem wir für Grad Celsius jetzt Kelvin einsetzen:

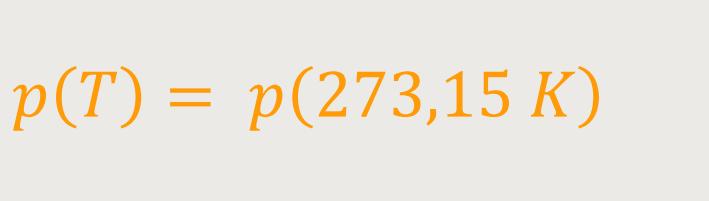
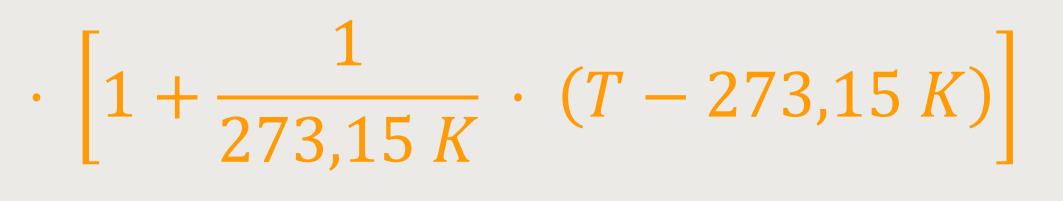
Was kommt nun dabei heraus? Durch noch­maliges Umformen ergibt sich:

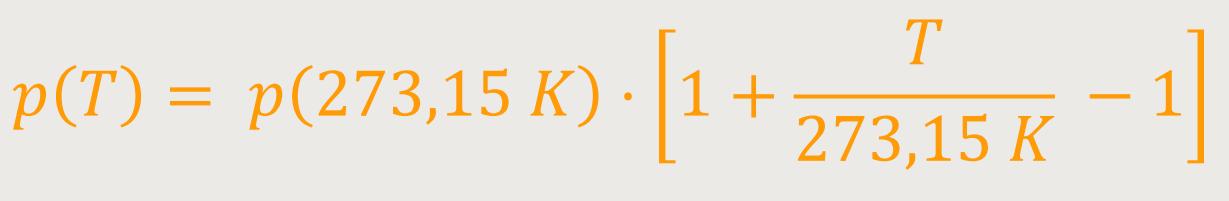
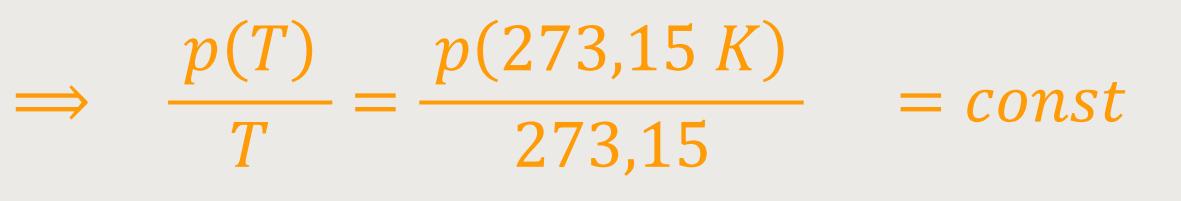
Nach wie vor gilt für das Volumen V = const.

Damit erhalten wir eine Beziehung, die beides erfüllt:

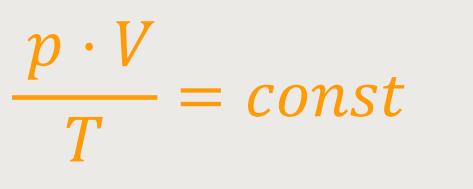
Diese Konstante ist ein Maß dafür, wie viel Moleküle in diesem System vor­handen sind. Also wie groß die Molekül­anzahl in dem Gas ist. Und dabei ist nun uner­heblich, welches Gas man verwendet. Daher wird diese Konstante auch geschrieben als:

n · R

R   ist die allgemeine Gaskonstante
n   ist die Molzahl

Man muss allerdings dazu sagen, dass diese Gaskonstante ein experi­menteller Befund ist. Und 1 Mol ist die­jenige Menge eines Gases oder einer Substanz, in der so viele Moleküle vorhanden sind, wie in 12 g vom Kohlenstoff­isotop 12C.

Und wenn man das entsprechend einsetzt, erhält man:

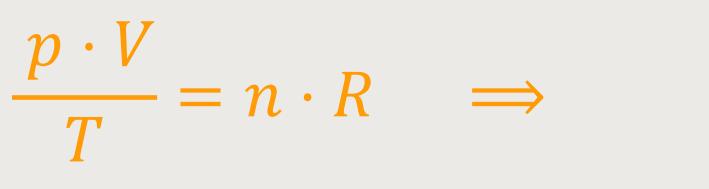
Das ist die Zustands­gleichung der idealen Gase.

⇦ Kapitel Kapitel ⇨