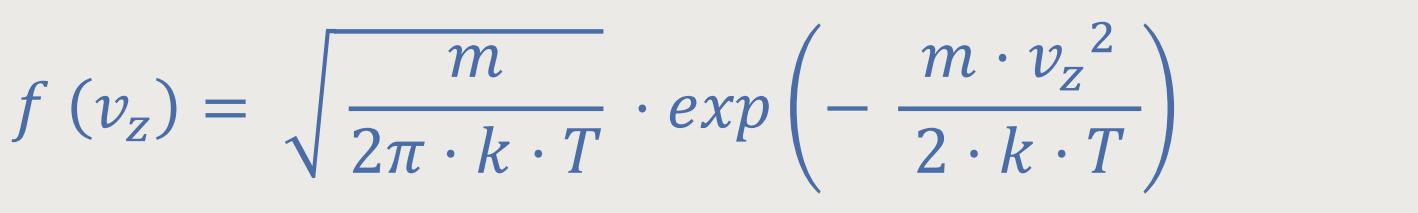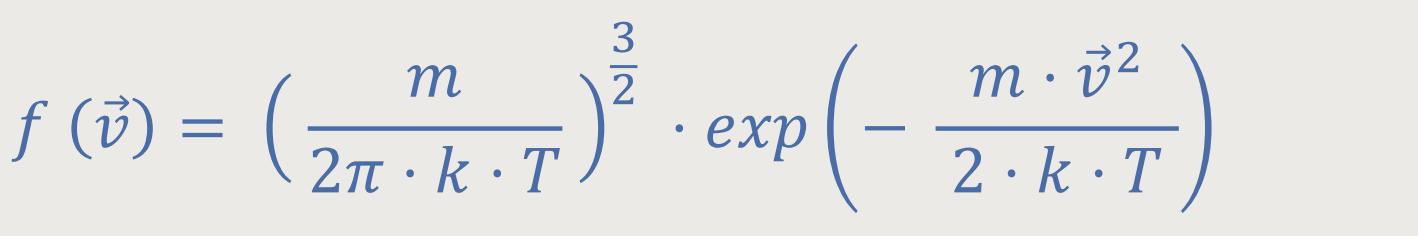Wie schaut denn nun die Vertei­lung der Geschwin­dig­keits­beträge aus?

Im vorherigen Kapitel hatten wir die normierte Wahr­schein­lich­keits­dichte für das Auftreten der z-Komponente der Geschwin­dig­keit wie folgt definiert:

In dem Exponenten wird mit (m · v_z²)/2 die kinetische Energie der Teil­chen für die Bewegung in Rich­tung der z-Achse angegeben.

Da man aber alle drei Raum­rich­tungen für die Bewegung eines Moleküls berück­sichtigen muss, kann man sich sozu­sagen die Spitze des Geschwin­dig­keits­vektors in einem kleinen Volumen­element, quasi dem Geschwin­dig­keits­raum vorstellen.

Man gibt dem Geschwin­dig­keits­vektor einen gewissen Bereich, in dem er schwanken kann. Und die Wahr­schein­lich­keit, dass der Vektor gerade so liegt, dass die Spitze des Geschwin­dig­keits­vektors in einem solchen Volumen­element eines hypothe­tischen Geschwin­dig­keits­raums liegt, ist dann gegeben als:

Und hier war f () · dv_x · dv_y · dv_z die Wahr­schein­lich­keit, dass:

die x-Komponente ∈ [v_x , v_x+dv_x] und
die y-Komponente ∈ [v_y , v_y+dv_y] und
die z-Komponente ∈ [v_z , v_z+dv_z] ist.

Wobei v_x , v_y , v_z die Kanten­längen eines solchen kleinen Würfels in einem Geschwin­dig­keits­raum entsprechen.

Und nachdem das lauter Und-Wahr­schein­lich­keiten sind, muss man die drei Komponenten mit­einander multi­pliziert werden. Man möchte erreichen, dass die Geschwin­dig­keiten dieses Moleküls zwischen v_x und v_x+dv_x und zwischen v_y und v_y+dv_y sowie zwischen v_z und v_z+dv_z liegen. Deshalb auch der Exponent 3/2.

Und wenn man die Exponen­tial­funktion für jede Komponente mit­einander multi­pliziert, dann addieren sich entspre­chend die Exponenten. Damit erhält man letzt­lich auch das m · ², wobei das ² natürlich dem v_x² + v_y² + v_z² entspricht.

Man kann hier schon erkennen, dass dieses f (v_z), wie bereits erwähnt, eine symme­trische Funktion ist.

Wesent­lich ist immer bei diesen Funktionen, diese mithilfe der Vorfaktoren so zu normieren, dass die Kurven in einem Graphen, und die sich daraus ergebenen Flächen, immer dem Wert 1 entsprechen. Ähnlich wie bei der Gaußschen Verteilung erhält man dann entspre­chende Kurven. Wobei der Vorfaktor so gewählt wird, dass ein entspre­chendes Integral gebildet wird, damit sich dann ergibt:

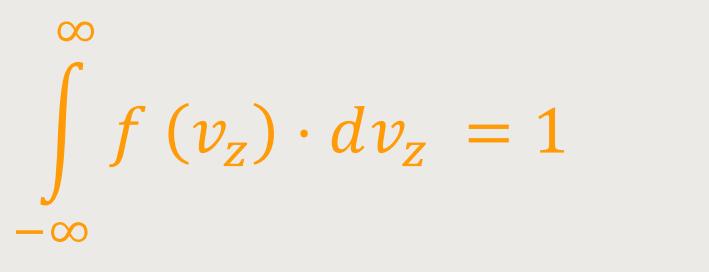
Dadurch erhält man auch eine Vergleich­barkeit der verschie­denen Tempe­ratur­kurven. Das f (v_z) hat die Dimension [s /m] und das v_z hat die Dimension [m /s], sodass das Produkt eine dimen­sions­lose Zahl ist und das Integral entspre­chend den Wert 1 hat.

Es geht aber immer noch um die Frage, wie schnell sind denn nun diese Moleküle? Was ist jetzt wirk­lich so eine typische mittlere Geschwin­dig­keit, mit der die Moleküle unter­wegs sind? Wir haben bisher immer nur über Kompo­nenten gesprochen. Ent­weder die z-Komponente oder den ganzen Geschwin­dig­keits­vektor, sprich alle drei Kompo­nenten x-y-z.

So wie uns, hat es seiner­zeit auch James Clerk Maxwell besonders inter­essiert, wie es mit den Geschwin­dig­keits­beträgen aussieht? Die können näm­lich nicht kleiner als Null werden. Insofern muss die Ver­teilungs­funktion anders dar­gestellt werden. Und zwar in einer solchen Form, dass man mehr Ein­blick in die tat­säch­lichen Geschwin­dig­keits­beträge erhält.

Hierzu kann man die Geschwin­dig­keits­vektoren ähnlich wie die Orts­vektoren in einem Raum auftragen. Die „Ausschläge” sind dann die Spitzen des Geschwin­dig­keits­vektors. Das ist aber nicht wirklich ein Raum der Anschauung, sondern nur eine gedachte Mög­lich­keit, die Geschwin­dig­keits­vektoren zu visuali­sieren.

Wenn man so vorgeht, verbreitet sich der Geschwin­dig­keits­raum von einem Ursprung aus. Genau gesagt, ein Geschwin­dig­keits­vektor zeigt von einem Ursprung mit dessen Spitze in Richtung eines kleinen Würfels. Die räum­lichen Komponenten dieses Würfels entspre­chen dv_x , dv_y und dv_z. Anschlie­ßend analysiert man die­jenigen Geschwin­dig­keiten, bei denen die Pfeilspitze im Inneren des Würfels liegen. So erhält man alle Geschwin­dig­keiten, die in Betracht kommen, und dieses f () · dv_x · dv_y · dv_z ist dann die Wahr­schein­lich­keit dafür, dass die Spitze des Geschwin­dig­keits­vektors in den Würfel rein ragt.

Natürlich hat so ein gedachter Raum gewisser­maßen auch ein Volumen. Denn dv_x · dv_y · dv_z ergibt das Volumen des Würfels. Es ist wohl­gemerkt kein Volumen im her­kömm­lichen Sinne, sondern ledig­lich ein gedachter Geschwin­dig­keits­raum.

Diese Idee des Geschwin­dig­keits­raums lässt sich in einer sehr praktischen Art und Weise anwenden. Jetzt kann man sich über­legen, wie verhält es sich, wenn man einen bestimmten Geschwin­dig­keits­betrag annimmt. Wenn man nichts als nur diesen Betrag vorgibt. Wie groß wird dann die Wahr­schein­lich­keit dafür sein, dass die Geschwin­dig­keit der Moleküle einen gewissen Betrag hat, und zwar unab­hängig davon, wohin der Vektor zeigt. Um das zu visualisieren, legt man jetzt in diesem Geschwin­dig­keits­raum rund um den Ursprungs­punkt eine Kugel­schale, also keinen Würfel wie oben, sondern eine geschlossene Kugel­schale.

Wenn jetzt ein Geschwin­dig­keits­vektor so liegt, dass seine Spitze gerade in dieser Kugel­schale hinein­ragt, dann bedeutet das, egal wohin er zeigt, dass der Betrag des Geschwin­dig­keits­vektors zwischen einem gewissen v und v+dv liegt. Wie lässt sich so etwas ausrechnen?

Das Volumen in dem Geschwin­dig­keits­raum gibt ja an, wie groß die Wahr­schein­lich­keit ist. Worauf es jetzt ankommt ist, das nicht mehr mit dem Volumen eines Würfels zu multi­plizieren, sondern mit dem Volumen der Hohl­kugel­schale. Es geht also darum, über diese Kugel­schale zu integrieren.

Die Kugel­schale hat im Geschwin­dig­keits­raum ein Volumen von:

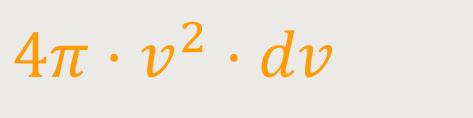
Um auf die Ver­teilungs­funktion der Geschwin­dig­keits­beträge zu kommen, ergibt sich entspre­chend:

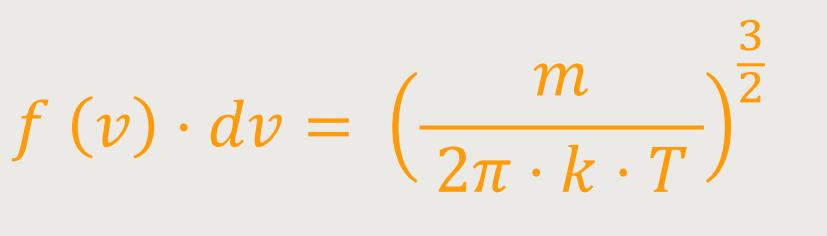
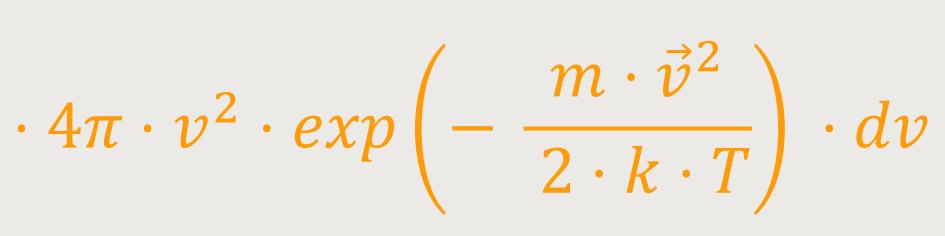
Und das nennt man die Maxwell-Boltzmann-Verteilung.

Diese Funktion gibt jetzt die Wahr­schein­lich­keit an, dass der Geschwin­dig­keits­betrag zwischen v und v+dv liegt.

Bei der Funktion wird mit einem Inter­vall der Geschwin­dig­keits­beträge multi­pliziert. Das heißt, die Geschwin­dig­keit, bei der die Wahr­schein­lich­keits­dichte-Funktion maximal ist, ist die wahr­schein­lichste Geschwindigkeit v_w. Da die Vertei­lungs­funktion im Diagramm aber auf der einen Seite quadra­tisch auf­steigt und nach Erreichen der maxi­malen Geschwin­dig­keit auf der Gegen­seite wieder exponen­tiell abfällt, ergibt sich somit eine unsym­metrische Funktion.

Aus diesem Grund wird die mittlere Geschwin­digkeit immer auf der Seite des exponen­tiellen Teils liegen, leicht versetzt zur maxi­malen Geschwin­digkeit. Diese mittlere Geschwin­digkeit teilt die Gesamt­fläche unter­halb der Ver­teilungs­funktion in zwei gleich­große Teil­flächen. Das ist dann der arith­metische Mittel­wert, bzw. die mittlere absolute Geschwin­digkeit ⟨ v⟩. Der arith­metische Mittel­wert des Geschwin­dig­keits­quadrats liegt noch weiter versetzt und ent­spricht dann √⟨ v²⟩. Das alles lässt sich durch Integration aus­rechnen. Auch die Positions­parameter auf der v-Achse im Diagramm, kann man entspre­chend aus­rechnen.

Die wahrschein­lichste Geschwin­dig­keit v_w wird definiert als:

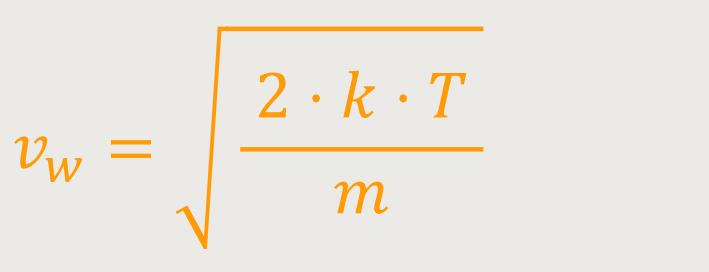
m   ist die Masse eines Moleküls

Die mittlere absolute Geschwin­dig­keit ⟨ v⟩ wird definiert als:

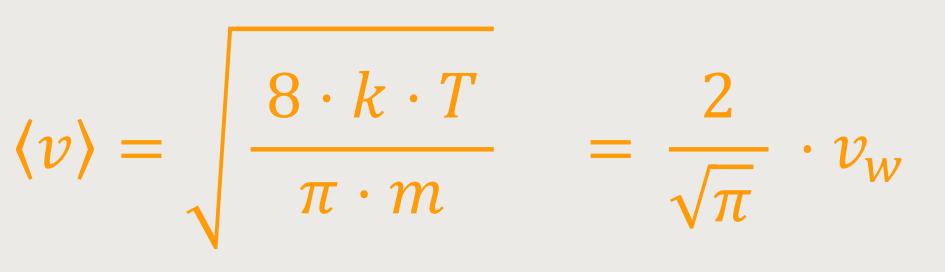
Die Wurzel (√) aus dem mittleren Geschwin­dig­keits­quadrat √⟨ v²⟩ wird definiert als:

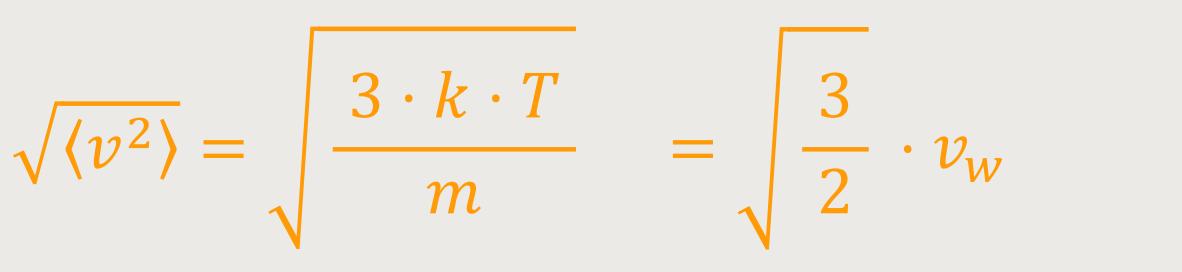
Damit ist es möglich, die realen Geschwin­dig­keiten eines Moleküls zu ermitteln. Die Moleküle von Stickstoff(N2) haben zum Beispiel bei 300 K eine mittlere Geschwin­dig­keit von 476 m/s. Das ist Über­schall­geschwindigkeit.

An dieser Stelle lässt sich über­prüfen, ob der Ausdruck für die Wurzel (√) aus dem mittleren Geschwin­dig­keits­quadrat mit der vor­herigen Betrach­tung über­einstimmt. Dort wurde die Temperatur mit der mittleren kinetischen Energie eines Gas­moleküls in Verbindung gebracht. Um das auch hier aus­rechnen zu können, muss man obige Gleichung über das mittlere Geschwin­dig­keits­quadrat nur quadrieren und anschließend durch 2 dividieren. Dann erhält man:

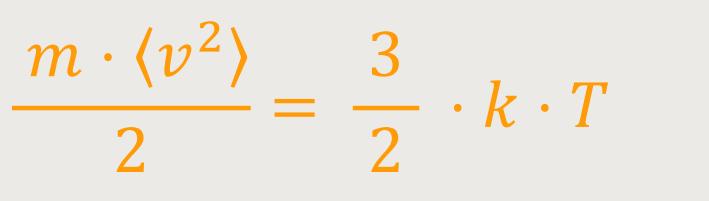
Diese Beziehung ist genau das, was wir bereits für die Tempe­ratur­definition erarbeitet haben. Das ent­spricht genau der mittleren kinetischen Energie eines Moleküls mit 3 Freiheits­graden. Somit ist die Definition der kinetischen Temperatur konsistent mit dem mittleren Geschwin­dig­keits­quadrat.

Wie bereits angesprochen, gibt es natür­lich auch Fluktua­tionen in der Thermo­dynamik. Einige Moleküle werden in ihrer Geschwin­dig­keit weit vom Durch­schnitt abweichen. Solche Fluktua­tionen können aber nur mithilfe der Mittel­werte nicht beschrieben werden. Dennoch kann man aus der Betrachtung des soge­nannten „Verteilungs­schwanzes” in einem Diagramm etwas ableiten.

Es gibt nämlich verschie­dene Vorgänge, die erst jenseits einer gewissen Energie aus­gelöst werden, wie beispiels­weise gas­chemische Reaktionen. Wenn man wissen will, ob diese Reaktionen mit irgen­deiner Rate ablaufen werden, sollte man abschätzen können, wie viele Moleküle es geben wird, die zufällig eine solche Energie bekommen, die dann groß genug ist, um diese Reaktion auszulösen. Laut Mittel­wert könnte das ja nie passieren. Aber wenn man die gesamte Ver­teilungs­funktion zugrunde legt, gibt es dann doch eine gewisse Wahr­schein­lich­keit, dass etwas passiert.

Oder wenn darum geht, Elek­tronen aus einer Metall­oberf­läche heraus­zu­schlagen. In einem solchen Fall kommt es wieder darauf an, ob die Energie der auf­tref­fenden Moleküle groß genug sein wird, um das zu bewerkstelligen. Selbst wenn die Mittel­werte keinen Hinweis darauf geben, gibt es dennoch ein paar Moleküle, oder Atome mit hoher Energie, die ein Atom aus der Ober­fläche heraus­lösen. Das heißt, eine solche Rate lässt sich mithilfe von Mittel­werten über­haupt nicht beschreiben, wohl aber mit den Ver­teilungs­funktionen. Das ist das Wichtige an diesen Funktionen.

Aller­dings befinden sich in unserer Luft so viele Moleküle, dass diese ständig mit­einander zusammen­stoßen. Wie groß ist denn die Distanz, die so ein Molekül über­haupt zurück­legen kann, bevor es wieder mit einem anderen zusammen­stößt?

Um diese Frage zu beantworten, betrachtet man die mittlere freie Weglänge.

Das erste, was wir in diesem Zusammen­hang unter­suchen wollen, ist der Stoß­querschnitt. Dafür approxi­miert man jetzt die Moleküle als elas­tische Kugeln mit Radius r_₁ und r_₂, die dann zwei Stoß­partner bilden. Man nimmt in der Regel an, dass zwei unter­schied­liche Stoß­partner auf­einander treffen. Durch die Elasti­zität kann man dann in verein­fachter Form einen Stoß­querschnitt definieren.

Dieser Stoß­querschnitt ent­spricht einer Kreis­fläche, dessen Radius aus zwei aneinandergesetzten Einzel­radien r_₁ + r_₂ gebildet wird. Man schlägt quasi diesen Gesamt­radius um den Mittel­punkt der einen Kugel, wobei der Radius des Stoß­querschnittes den Mittel­punkt der anderen Kugel schneidet. Und was dann inner­halb dieses Stoß­quer­schnittes liegt, wird dann wirklich getroffen:

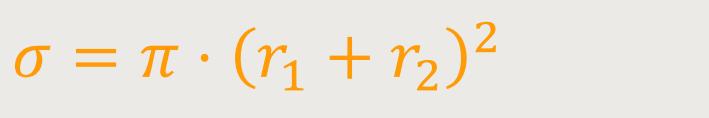
σ   ist der Stoßquerschnitt

Abb.: Der Stoßquerschnitt zweier Moleküle

Immer wenn der Mittel­punkt des zweiten Moleküls inner­halb eines Stoß­quer­schnittes liegt, kommt es zu einem Zusammen­treffen der Moleküle. Um jetzt die mittlere freie Weg­länge zu berechnen, geht man so vor, dass man sich nur ein einzelnes Gas­molekül denkt, welches sich durch die ganze Population der anderen umgebenden Gas­moleküle hindurch­bewegt.

Des Weiteren setzt man voraus, dass die anderen Moleküle hypothe­tisch in Ruhe verharren. Die Anzahl der Moleküle pro Volumen­einheit ergibt dann eine Teilchen­anzahl­dichte n.

Man stellt sich also vor, wie sich ein einzelnes Molekül, durch diese Population hindurch bewegt. An dem Molekül angeheftet ist sein Wirkungs­querschnitt. Viel­leicht bewegt es sich längs einer Weg­strecke x durch das System, welches man als Zylinder andeuten könnte. Entschei­dend ist jetzt, ob dieses Molekül während seiner Bewegung mit einem anderen in Kontakt tritt. Das wird dann der Fall sein, wenn irgen­dein Mittel­punkt eines anderen Teilchens inner­halb des Zylinder­volumens des ersten Moleküls hinein­taucht bzw. sich über­schneidet.

Letzten Endes betrachtet man das Volumen dieses Zylinders. Das Volumen ist nichts anderes als σ · x. Die Distanz, die das betrachtete Molekül auf der Strecke x zurück­legt, bevor es auf ein anderes trifft, nennt man die „mittlere freie Weglänge”. Die Weg­länge, die das Molekül mitsamt seinem angehängten Quer­schnitt zurücklegt, bis es im Durch­schnitt 1 Molekül trifft, ist definiert als:

σ   ist der Stoßquerschnitt
λ   ist die mittlere freie Weglänge des Moleküls
n   ist die Teilchenanzahldichte

Daraus ergibt sich, je dichter die Teilchen liegen, desto kleiner ist die mittlere freie Weglänge. Oder aber, wenn der Stoßquerschnitt größer wird, kommt es ebenfalls eher zu einem Stoß, und die mittlere freie Weglänge verringert sich analog.

Obiger Fall gilt nur unterer der Voraussetzung, dass sich die umgebende Population in Ruhe befindet. In der Realität ist das aber nicht so, denn die Moleküle zittern alle herum. Und so kommt es zwangs­läufig zu mehr Stößen, die berück­sichtigt werden müssen. Insofern ändert sich die Gleichung noch etwas:

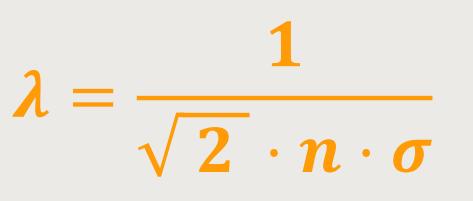
Das ist die mittlere freie Weglänge eines Moleküls in einem Gas.

Wenn man jedoch Gemische von verschie­denen Substanzen betrachtet, wird die Berechnung etwas komplizierter. Für unsere Atmosphäre, die zu 78% aus Stickstoff(N2) besteht, ergibt sich unter Normal­beding­ungen eine mittlere freie Weglänge von λ = 60 nm.

Aber bei der Geschwin­dig­keits­verteilung geht es natür­lich auch immer um die Temperatur in einem System. Wir hatten bereits in Verbindung mit der Kinetik idealer Gase den Begriff Wärme­kapazi­tät kurz behandelt. Im nächsten Kapitel wollen wir das Thema Wärme­kapazi­tät noch etwas genauer beleuchten.

⇦ Kapitel Kapitel ⇨