Bei der Beschreibung der uns umgebenden Natur lassen wir uns insbesondere von unseren Sinnesorganen leiten. Insofern weiß man sehr gut, was heiß und kalt ist. Aber das ist kein quantitatives Sinnesorgan. Subjektiv betrachtet sagt man, wenn es sehr heiß ist, „man verbrennt sich”, und wenn es sehr kalt ist, dann „friert man”. Aber um welchen genauen Betrag es sich jeweils ändert, dafür hat man kein Sinnesorgan. Außer vielleicht das Thermometerhuhn mit seinem Schnabel. Aber in der Physik will man alles möglichst genau quantifizieren, damit man irgendwelche Gesetzmäßigkeiten aufstellen kann. Und daher muss man den Sachverhalt genauer betrachten.
Um der „Temperatur” eine konkrete Bedeutung zu geben, lässt sich das mit dem thermodynamischen Gleichgewicht veranschaulichen. Man sagt, wenn zwei Körper, die miteinander in Kontakt sind, sich im thermodynamischen Gleichgewicht befinden, dann sind sie stets auf gleicher Temperatur. Wenn man zum Beispiel zwei Metallkörper miteinander in Berührung bringt, kommt es zu einem Kontakt, und wenn man eine Zeit lang wartet, um ein thermodynamisches Gleichgewicht herzustellen, dann werden diese zwei Körper schließlich auf gleicher Temperatur sein.
Hierbei kommt es gar nicht darauf an, wie groß die Massen dieser Körper sind. Sie werden immer in ein Gleichgewicht kommen, es kann nur sein, dass es länger dauert. Das lässt sich auch nicht beschleunigen, denn die Thermodynamik ist eine langsame Wissenschaft. Die Thermodynamik lebt von Gleichgewichtszuständen, und man muss in der Regel warten, bis diese erreicht sind. Daher ist die Temperatur nicht proportional zur Masse. Wenn man einen doppelt so großen Körper hat, ist die Temperatur trotzdem die gleiche. Daher nennt man die Temperatur eine „intensive Größe”, weil sie nicht proportional zur Masse des Körpers ist.
Allerdings ist die Wärmemenge, die in einem Körper enthalten ist, sehr wohl proportional nur Masse. Bei einem kleinen Topf mit Wasser muss man weniger Wärme zuführen, als bei einem großen Topf. Das heißt, der Wärmeinhalt ist proportional zur Masse des Körpers, aber seine Temperatur nicht. Es besteht also ein Unterschied zwischen der Temperatur eines Körpers und seinem Wärmeinhalt. Beides lässt sich statistisch sehr schön untermauern. Wie kann man denn die Temperatur überhaupt messen?
Grundsätzlich gibt es verschiedene Methoden, die Temperatur zu bestimmen. Das hängt damit zusammen, dass es verschiedene makroskopische Systeme gibt, die ganz individuell auf Temperaturunterschiede reagieren. Ein klassisches Beispiel dafür sind die Phasenübergänge beim Wasser. Unterhalb einer gewissen Temperatur gefriert es. Aber oberhalb einer gewissen Temperatur siedet es. Und bei genauer Beobachtung stellt sich heraus, dass es insbesondere beim Gefrieren immer bei derselben Temperatur passiert. Wenn etwas gerade friert, oder in umgekehrter Richtung zu schmelzen beginnt, hat man einen Fixpunkt. Die ursprüngliche Definition der Temperaturmessung geht also über die Fixpunkte des Wassers.
Und das nennt man auch die „Celsius-Temperatur” tc.
Wenn diese Temperatur gleich
Für „Präzisionsmessungen” werden dagegen gewisse Fixpunkte
über einen möglichst weiten Temperaturbereich gesetzt. Ein Fixpunkt ist
die erwähnte Celsius-Temperatur tc. Wenn diese
Temperatur bei
Ein weiterer Fixpunkt liegt bei
Oder bei
Aber mit diesen Fixpunkten allein ist es nicht getan. Um wirklich zu einer Interpretation beliebiger Temperaturen zu kommen, kommt es darauf an, dass man zwischen diesen Fixpunkten interpoliert. Und da berücksichtigt man verschiedene thermische Eigenschaften von Körpern, insbesondere sind das mechanische Eigenschaften.
Bei Temperaturveränderungen ändert sich nämlich auch die Länge eines Körpers. Und so lässt sich die Länge bei einer bestimmten Temperatur wie folgt beschreiben:
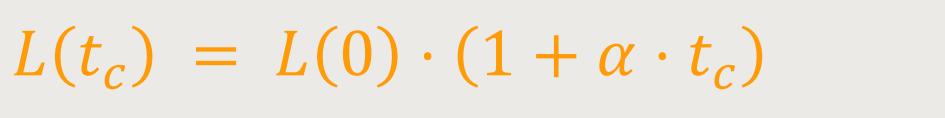
L(0) ist die Anfangslänge, bei 0 °C
α ist der lineare Ausdehnungskoeffizient
Der lineare Ausdehnungskoeffizient ist bei jedem Material unterschiedlich.
Alternativ dazu gibt es auch die Möglichkeit, eine Volumenänderung, beispielsweise von einer Flüssigkeit, zu betrachten. Das Volumen bei einer bestimmten Temperatur tc verhält sich dann ähnlich:
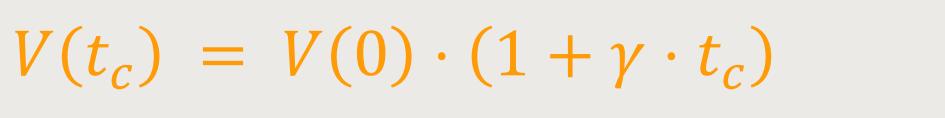
γ ist der räumliche Ausdehnungskoeffizient
Doch wenn man genau genug hinschaut, stellt man fest, dass nichts linear ist. Es ist immer nur die Frage, über welche begrenzten Bereiche man Nichtlinearitäten noch berücksichtigen kann oder nicht. Vor allem wenn ein Körper oder Medium schmilzt. Die Annahme einer Linearität ist in den meisten Fällen nur dann begründet, wenn die Bereiche, über die sich die Variablen verändern, klein genug sind, sodass man Abweichungen von der Nichtlinearität vernachlässigen kann.
Nicht nur mechanische, sondern auch elektrische Eigenschaften sind temperaturabhängig. Zum Beispiel ist die Kontaktspannung zwischen zwei miteinander verbundenen unterschiedlichen Metallen wie Kuper und Zink, das eine ist edler und das andere weniger edel, von der Temperatur abhängig. Hierbei spricht man auch von der Methode des „Thermoelements”.
Es gibt aber noch ein anderes Medium, das sich besonders leicht beschreiben lässt. Insbesondere die Gase und speziell verdünnte Gase, wozu auch die Luft gehört, nehmen eine Sonderstellung ein. Die Moleküle in dem Gas haben nämlich untereinander praktisch keine Wechselwirkung, außer sie stoßen gerade zusammen und das ist dann ein elastischer Stoß. Mit den oben genannten Voraussetzungen lassen sich diese Systeme besonders gut theoretisch beschreiben. Deswegen wenden wir uns jetzt als nächstes den idealen Gasen zu und den dort vorhandenen Gesetzmäßigkeiten.
⇦ Kapitel Kapitel ⇨
