Minkowski wies darauf hin, dass es für seine Betrach­tungs­weise der Gruppe G_c unumgäng­lich sei, das Verständnis der physika­lischen Zusammen­hänge auf Basis von Minkowskis Über­legungen zu über­arbeiten, damit es zu keinem Wider­spruch bei den physika­lischen Gesetzen führt. Eine solche Über­arbeitung habe nach Minkowskis Worten in einem gewissen Umfang bereits im Bereich der Thermo­dynamik und der Wärme­strahlung, sowie für die elektro­magne­tischen Vorgänge und nicht zuletzt in der Mechanik, was den Begriff der „Masse” angeht, statt­gefunden.

Insbesondere zum Bereich der Mechanik warf Minkowski die Frage auf, wenn eine Kraft mit den Kompo­nenten 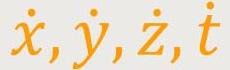X, Y, Z, entspre­chend der Raum­achsen, in einem Welt­punkt P(x, y, z, t) angreift, in welchem zugleich der Bewegungs­vektor liegt, als was für eine Kraft kann diese Kraft bei einer beliebigen Änderung des Bezugs­systems auf­gefasst werden?

Minkowski wies auf die nachweis­baren Fort­schritte zum Thema „pondero­motorische Kraft” im elektro­magne­tischen Feld hin, welche sich auf die betrachtete Gruppe G_c über­tragen lassen. Unter der ponderomotorischen Kraft versteht man heute den nieder­frequenten Anteil der Kraft eines räum­lich inhomogenen, hoch­frequenten elektro­magne­tischen Feldes auf ein System von (sich in diesem Feld bewegenden) elek­trischen Ladungen.

Die damaligen Ansätze veranlassten Minkowski zu einer einfachen Regel:
Bei der Änderung des Bezugs­systems ist die voraus­gesetzte Kraft in der Weise als eine Kraft in den neuen Raum­koordinaten anzusetzen, dass dabei der zuge­hörige Vektor mit den Komponenten

... bei denen

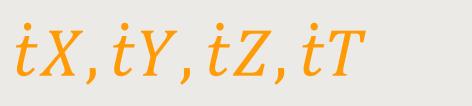
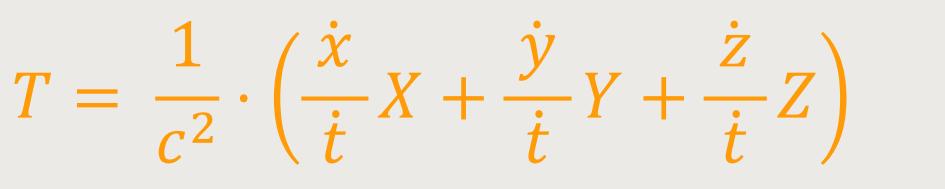
... die durch c² dividierte Arbeits­leistung der Kraft im Welt­punkt ist, unver­ändert bleibt.

Dieser Vektor ist stets normal zum Bewegungs­vektor im Punkt P. Ein solcher, zu einer Kraft im Punkt P gehörende Kraft­vektor, bezeichnete Minkowski als ein sich „bewegender Kraft­vektor im Punkt P”.

Im weiteren Verlauf soll die durch diesen Punkt P ver­laufende Welt­linie, die ja den substan­ziellen Punkt wider­spiegelt, mit konstanter mecha­nischer Masse m beschrieben werden. Das m-fache, des Bewegungs­vektors im Punkt P soll als der „Impuls­vektor in P” bezeichnet werden. Wogegen das m-fache, des Beschleu­nigungs­vektors im Punkt P als der „Kraft­vektor der Bewegung in P” bezeichnet werden soll.

Diese Definitionen beschreiben das Gesetz dafür, wie die Bewegung eines Massen­punktes bei gegebenem sich bewegenden Kraft­vektor statt­findet. Damit soll gelten:
Der Kraft­vektor der Bewegung ist gleich dem bewegenden Kraft­vektor.

Nach Minkowskis Ansicht, fasst diese Aussage die vier Gleichungen für die Komponenten nach den vier Achsen zusammen. Wobei die vierte Gleichung, weil von vorn­herein beide genannten Vektoren normal zum Bewegungs­vektor angeordnet sind, sich als eine Folge der drei ersten Gleichungen ansehen lässt. Nach der obigen Bedeutung von T stellt die vierte Gleichung zweifellos den Energie­satz dar. Als kinetische Energie des Massen­punktes ist daher der c²-fache der Kompo­nente des Impuls­vektors nach der t-Achse zu definieren.

Daraus ergibt sich die Beziehung:

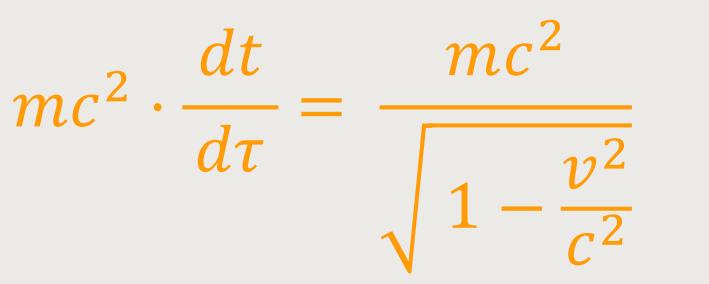
Das entspricht nach Abzug der additiven Konstante mc² dem Ausdruck ½ mv² der Newton'schen Mechanik bis auf die Größen von der Ordnung 1/c². Sehr anschau­lich erscheint hierbei die Abhängig­keit der Energie vom Bezugs­system. Da nun aber die t-Achse in die Richtung jedes zeit­artigen Vektors gelegt werden kann, enthält ander­seits der Energie­satz, für jedes mögliche Bezugs­system, bereits das ganze System der Bewegungs­gleichungen.

Diese Tatsache behält bei dem angespro­chenen Grenz­wert bei c = ∞ ihre Bedeutung auch für den Aufbau der Axiome der Newton'schen Mechanik, was bereits in solchem Sinn von J.R. Schütz (1897) fest­gestellt worden sei.

Nach Aussage von Minkowski lässt sich von vorn­herein das Verhältnis von Längen­einheit zu Zeit­einheit so wählen, dass dies der natür­lichen Geschwindig­keits­schranke c = 1 ent­spricht. Führt man dann die Beziehung (√-1) · t = s an Stelle von t ein, so erhält man folgenden quadra­tischen Differential­ausdruck:

Dadurch zeigt sich eine völlige Symmetrie in x, y, z, s, und diese Symmetrie ist auf jedes Gesetz über­tragbar, welches dem Welt­postulat nicht wider­spricht. Man kann hiernach das Wesen dieses Postulats mathe­matisch sehr prägnant in die mystische Formel kleiden:

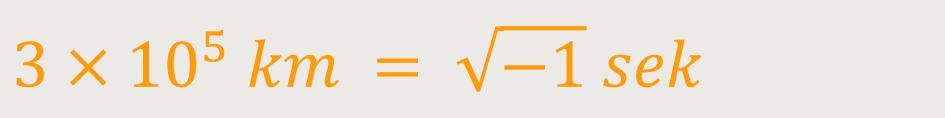
Die Vorteile, die sich aus dem Welt­postulat ergeben, werden durch nichts so treffend belegt, wie durch die Beschreibung des Verhaltens einer beliebig bewegten punkt­förmigen Ladung nach den in der Maxwell-Lorentzschen Theorie beschrie­benen Wechsel­wirkungen.

Stellen wir uns diesbezüg­lichen die Welt­linie eines punkt­förmigen Elektrons mit der Lage e vor, und führen auf ihr die Eigen­zeit τ ein, wobei die betref­fende Welt­linie an irgend­einem Punkt beginnt. Um das vom Elektron in einem beliebigen Welt­punkt P₁ angeregte Feld zu erhalten, konstruieren wir den zum Punkt P₁ dazugehörigen Vorkegel (Abb. 4).

Abb. 3: Zeigt die von Minkowski skizzierte Weltlinie eines punktförmigen Elektrons

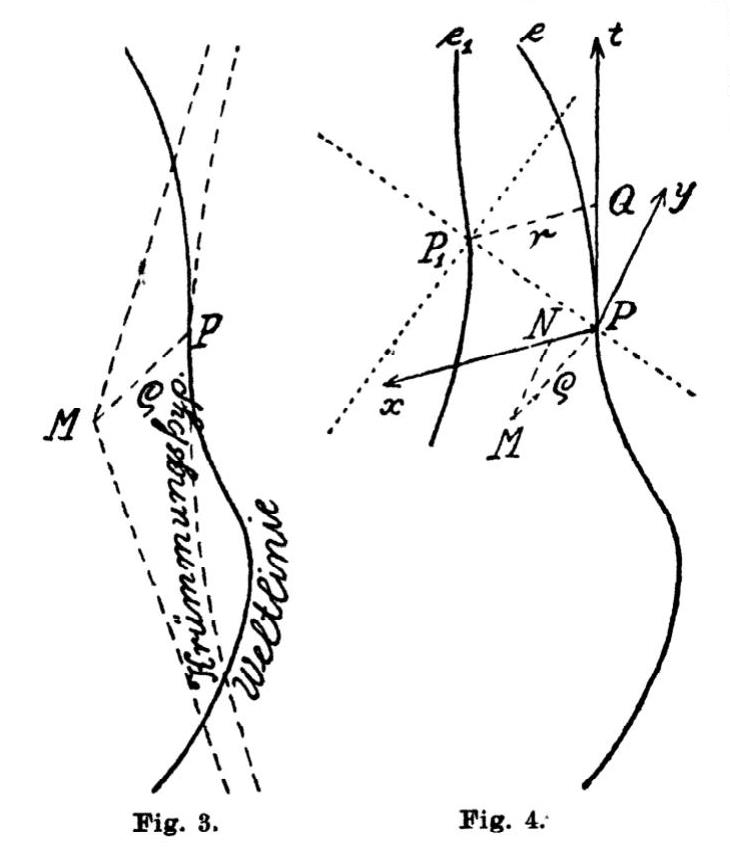
Dieser Vorkegel trifft die unbegrenzte Welt­linie des betrachteten Elektrons, weil deren Richtungen überall denen von zeit­artigen Vektoren ent­sprechen, offenbar in einem einzigen Punkt P. In diesem Punkt P wird an die Welt­linie eine Tangente gelegt und anschlie­ßend durch den Punkt P₁ die Normale P₁Q auf diese Tangente konstruiert. Der Betrag von P₁Q ent­spricht dem Radius r. Als Betrag von PQ ergibt sich gemäß der Definition eines Vor­kegels der Wert r/c. Nun stellt der Vektor in Richtung PQ mit dem Betrag e/r in seinen Kompo­nenten nach den x-,y-,z-Achsen das mit c multi­plizierte Vektor­potential dar. Und in der Kompo­nente nach der t-Achse stellt das skalare Potential des von e erregten Feldes für den Welt­punkt P₁ dar. Das entspräche den seiner­zeit von A. Liénard und E. Wiechert aufge­stellten Elementar­gesetzen, so wie sie damals verstanden wurden.

Bei der Beschreibung des von diesem Elektron angeregten Feldes zeigt sich, dass die Trennung des Feldes in eine elekt­rische und eine magne­tische Kraft relativ ist, wegen der zugrunde gelegten Zeit­achse. Minkowski zog den Vergleich heran, das man diese beiden Kräfte, wenn auch nicht in einer völlig zutreffenden Analogie, mit einer Kraft­schraube in der Mechanik vergleichen werden könnte.

Minkowski beschreibt nachfolgend die von einer beliebig bewegten punkt­förmigen Ladung auf eine andere beliebig bewegte punkt­förmige Ladung ausgeübte pondero­motorische Wirkung.

Hierzu fügen wir gedank­lich durch den Welt­punkt P₁ eine weitere Welt­linie eines zweiten punkt­förmigen Elektrons mit der Ladung e₁ hinzu. Wir behalten die Punkte P, Q, r bei, und konstruieren (siehe Abb. 4) den Mittelpunkt der Krümmungs­hyperbel im Punkt P, und fügen die Normale MN vom Punkt M aus hinzu. Wir erhalten eine durch P parallel zu QP₁ gedachte Gerade.

Nun legen wir noch ein Bezugs­system fest, mit P als Anfangs­punkt, und legen die 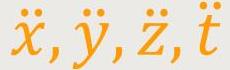t-Achse in die Richtung PQ, die x-Achse in die Richtung QP₁ und die y-Achse in die Richtung MN. Dadurch ist schließlich auch die Richtung der z-Achse als normal zu den t-, x-, y-Achsen bestimmt. Der Beschleu­nigungs­vektor im Punkt P sei und der Bewegungs­vektor im Punkt P₁ sei .

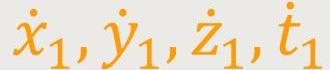Jetzt erhält man den von dem ersten beliebig bewegten Elektron e auf das zweite beliebig bewegte Elektron e₁ im Punkt P₁ ausgeübten und sich bewegenden Kraft­vektor:

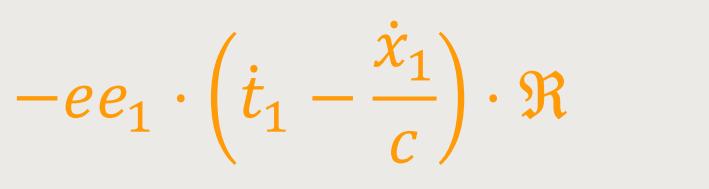
Wobei für die Komponenten ℜ_x, ℜ_y, ℜ_z, ℜ_t des Vektors ℜ die drei Relationen bestehen:

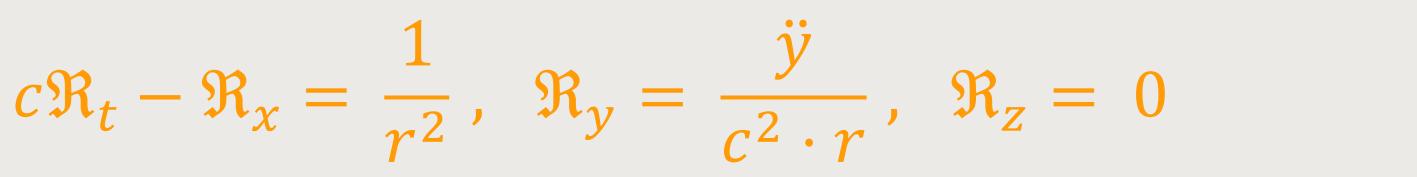
Und als viertes steht dieser Vektor ℜ normal zum Bewegungs­vektor im Punkt P₁ , und durch diesen Umstand allein in Abhängig­keit vom letzteren Bewegungs­vektor.

Vergleicht man mit dieser Aussage die bisherigen Formu­lierungen z.B. von K. Schwarzschild, nämlich des Elementar­gesetzes über die pondero­motorische Wirkung bewegter punkt­förmiger Ladungen aufeinander, so kommt man nicht umhin zuzugeben, dass die hier in Betracht kommenden Verhält­nisse ihr inneres Wesen erst in vier Dimensionen offen­baren. Man muss es quasi nur von einem vorge­gebenen 3-dimen­sionalen Raum auf eine entspre­chende Abbildung über­tragen.

Laut Aussage von Minkowski fallen in einer Mechanik, die aufgrund obigen Welt­postulats über­arbeitet werden müsste, die Diskrepanzen zwischen der Newton'schen Mechanik und der modernen Elektro­dynamik von selbst weg.

Minkowski bewertete abschließend noch die Stellung des Newton'schen Attraktions­gesetzes, heute als „Gesetz der Gravitation” bekannt, in Bezug auf obiges Postulat. Er nahm an, wenn zwei Massen­punkte m, m₁ jeweils ihre Welt­linie beschreiben, würde von m auf m₁ ein in Bewegung befindlicher Kraft­vektor ausgeübt. Und zwar so, wie er zuvor in Verbindung mit den Elektronen beschrieben wurde, nur dass für −ee₁ jetzt +mm₁ eingesetzt wird.

Wir betrachten nun den speziellen Fall, dass der Beschleu­nigungs­vektor von m konstant Null ist, wobei wir anschlie­ßend t so einsetzen, dass m als ruhend auf­gefasst werden kann. Zusätz­lich erfolgt die Bewegung von m₁ allein durch den von m bewirkten Kraft­vektor. Nun wird dieser definierte Kraft­vektor zunächst durch Hinzufügen folgenden Faktors erweitert:

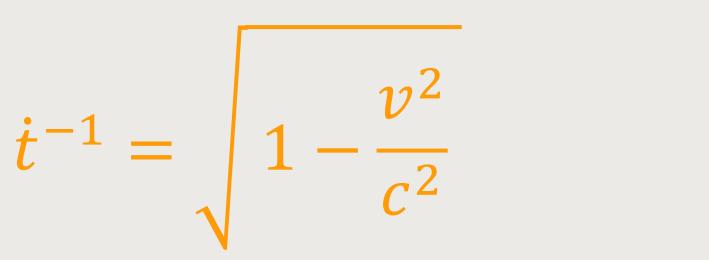
Bei Größen von der Ordnung von 1/c² auf 1 zeigt sich, dass für die Koordinaten x₁, y₁, z₁ von der Masse m₁ und deren zeit­lichen Verlauf genau wieder die Keplerschen Gesetze Anwendung finden. Aller­dings würden dabei an die Stelle der Zeiten t₁ die Eigen­zeiten τ₁ von m₁ treten. Auf­grund dieser ein­fachen Anmerkung kann man schnell erkennen, dass das vorge­schlagene Gravita­tions­gesetz verknüpft mit der über­arbeiteten Mechanik, nicht weniger gut geeignet ist, die astro­nomischen Beobachtungen zu erklären, genauso wie das Newton'sche Gravita­tions­gesetz verknüpft ist mit der Newton'schen Mechanik.

Auch die Grund­gleichungen für die elektro­magne­tischen Vorgänge in massebe­hafteten Körpern fügen sich durchaus in das Welt­postulat ein. Sogar die von Lorentz gelehrte Ableitung dieser Gleichungen auf Grund­lage der Elektronen­theorie braucht letzt­lich nicht über Bord geworfen zu werden, wie Minkowski dies an anderer Stelle beabsichtigte aufzuzeigen.

Die Gültig­keit obigen Welt­postulats ohne Einschrän­kungen ist, so war Minkowski davon über­zeugt, der wahre Kern eines elektro­magne­tischen Welt­bildes, der von Lorentz ersonnen, und von Einstein weiter ausgeführt wurde. Beim Ausarbeiten der mathe­matischen Konse­quenzen werden genug Hinweise auf experi­mentelle Verifika­tionen des Postulats zu finden sein, um auch diejenigen zu über­zeugen, denen es schwer fällt, alt­gewohnte Anschauungen aufzugeben, und durch eine im Voraus festgestellte Einheit zwischen der reinen Mathe­matik und der Physik zu beschwichtigen.

⇦ Kapitel Kapitel ⇨