Laut Einstein hat das vorher Betrachtete gezeigt, dass das allgemeine Relativi­täts­postulat zu der Forderung führt, dass die Gleichungs­systeme der Physik beliebigen Substitu­tionen der Koordi­naten x₁ ... x₄ gegen­über kovariant sein müssen. Aus diesem Grund müsste die Über­legung ange­stellt werden, wie der­artige all­gemein kovariante Gleichungen gewonnen werden können. Dieser rein mathe­matischen Aufgabe wandte sich Einstein im Nach­folgenden zu. Nach seinen Worten würde sich dabei zeigen, dass bei deren Lösung die in Gleichung (3) angegebene Invariante ds eine funda­mentale Rolle spielen wird, welche in Anlehnung an die Gaußsche Flächen­theorie als „Linien­element” bezeichnet wurde.

Der Grund­gedanke dieser all­gemeinen Kovarianten­theorie ist folgender: Es seien gewisse Sach­verhalte („Tensoren”) mit Bezug auf jedes Koordi­naten­system durch eine Anzahl Raum­funk­tionen definiert, welche die „Komponenten” des Tensors genannt werden. Es gibt dann gewisse Regeln, nach welchen diese Kompo­nenten für ein neues Koordinaten­system berech­net werden, wenn sie für das ursprüng­liche System bekannt sind. Außerdem muss die Trans­formation bekannt sein, die beide Systeme mit­einander ver­knüpft. Die nachher als „Tensoren” bezeichneten Sach­verhalte sind ferner dadurch gekenn­zeichnet, dass die Trans­formations­gleichungen für ihre Komponenten linear und homogen sind. Demnach würden sämt­liche Komponenten im neuen System ver­schwinden, wenn sie im ursprüng­lichen System gänzlich ver­schwinden. Wird also ein Natur­gesetz durch das Null­setzten aller Komponenten eines Tensors formuliert, so ist es allgemein kovariant. Indem man die Bildungs­gesetze der Tensoren unter­sucht, erhält man die Mittel zur Auf­stellung allgemein kovarianter Gesetze.

Hinweis: Man könnte auch sagen, das die Tensoren das Trans­formations­verhalten der Basis­vektoren beschreiben.

§ 5. Kontravarianter und kovarianter Vierervektor.

Kontravarianter Vierer­vektor. Das Linien­element ist definiert durch die vier Kompo­nenten dx_ν, deren Trans­forma­tions­gesetz durch folgende Gleichung ausge­drückt wird: (5)

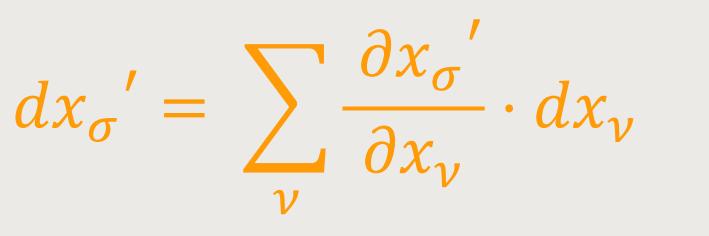
Die dx_σ' drücken sich linear und homogen durch die dx_ν aus. Man kann diese Koordi­naten­differentiale dx_ν daher als die Kompo­nenten eines Tensors ansehen, der speziell als „kontra­varianter Vierer­vektor” bezeichnet wird. Jeder Sach­verhalt, der bezüg­lich des Koordi­naten­systems durch vier Größen A^ν definiert ist, und die sich nach folgen­dem Gesetz (5a)

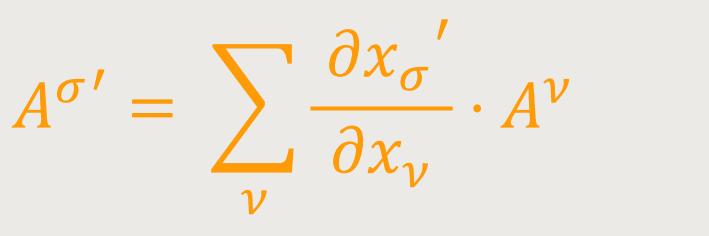
transformieren, bezeichnen wir eben­falls als kontra­varianten Vierer­vektor. Aus (5a) folgt sogleich, dass die Summen (A^σ ± B^σ) eben­falls Kompo­nenten eines Vierer­vektors sind, wenn A^σ und B^σ es sind. Entspre­chend gilt für alle später als „Tensoren” einzu­führenden Systeme die Regel von der Addition und Subtraktion der Tensoren.

Kovarianter Vierer­vektor. Die vier Größen A_ν werden als die Kompo­nenten eines „kovarianten Vierer­vektors” bezeichnet, wenn für jede beliebige Wahl des Kontra­varianten Vierer­vektors B^ν gilt: (6)

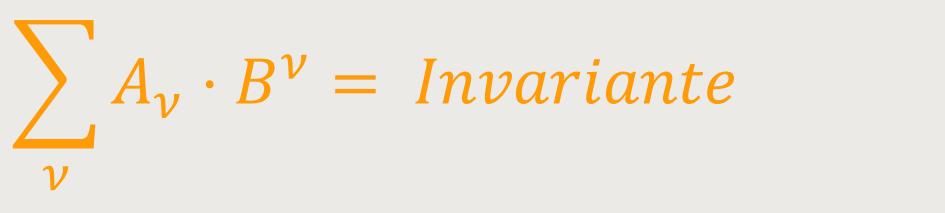
Aus dieser Definition folgt das Trans­formations­gesetz des kovarianten Vierer­vektors. Ersetzt man nämlich auf der rechten Seite folgender Gleichung

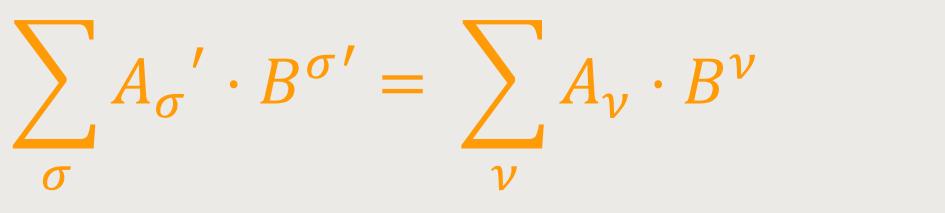
das B^ν durch den aus der Umkehrung der Gleichung (5a) folgenden Ausdruck

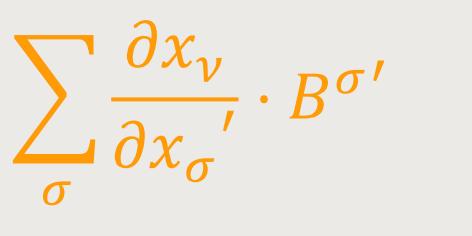
so erhält man

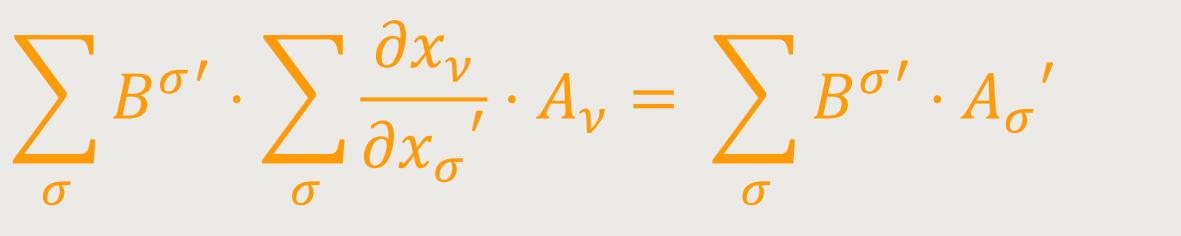
Hieraus folgt aber, weil in dieser Gleichung die B^σ' unabhängig von­einander frei wähl­bar sind, folgendes Trans­formations­gesetz: (7)

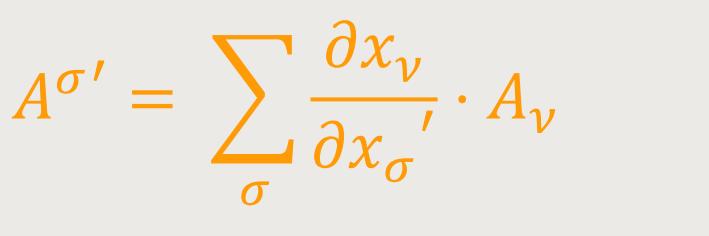
Bemerkung zur Vereinfachung der Schreibweise der Ausdrücke.

Ein Blick auf die Gleichungen dieses Paragraphen zeigt, dass über Indizes, die zweimal unter einem Summen­zeichen auf­treten [z.B. der Index ν in (5)], stets summiert wird, und zwar nur über zweimal auf­tretende Indizes. Es ist deshalb mög­lich, ohne die Klar­heit zu beeinträch­tigen, die Summen­zeichen wegzu­lassen. Dafür führte Einstein folgende Vorschrift ein: Tritt ein Index in einem Term eines Ausdrucks zweimal auf, so ist über ihn stets zu summieren, wenn nicht ausdrück­lich das Gegen­teil bemerkt ist.

Der Unterschied zwischen dem kovarianten und kontra­varianten Vierer­vektor liegt in dem Trans­formations­gesetz (7) bzw. (5). Beide Gebilde sind Tensoren im Sinne der obigen all­gemeinen Bemerkung. Hierin liegt laut Einstein ihre Bedeutung. In Anleh­nung an Ricci und Levi-Civita wird der kontra­variante Charakter durch „oberen”, der kovariante durch „unteren” Index bezeichnet.

§ 6. Tensoren zweiten und höheren Ranges

Kontravarianter Tensor. Bildet man sämtliche 16 Produkte A^μν der Kompo­nenten A^μ und B^ν zweier kontra­varianten Vierer­vektoren wie folgt: (8)

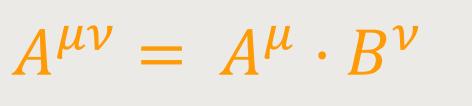
so erfüllt A^μν gemäß (8) und (5a) folgendes Trans­formations­gesetz: (9)

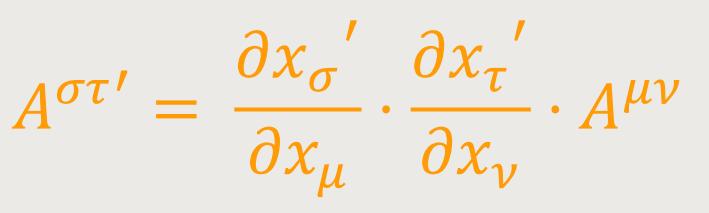
Man nennt einen Sach­verhalt, der bezüg­lich eines jeden Bezugs­systems durch 16 Größen (Funktionen) beschrieben wird, die das Trans­formations­gesetz (9) erfüllen, einen kontra­varianten Tensor „zweiten Ranges”. Nicht jeder solcher Tensor lässt sich gemäß (8) aus zwei Vierer­vektoren bilden. Aber es sei nach Einsteins Ansicht leicht zu beweisen, dass sich 16 beliebig gegebene A^μν dar­stellen lassen als die Summe der A^μ B^ν von vier geeignet gewählten Paaren von Vierer­vektoren. Deshalb könnte man beinahe alle Sätze, die für den durch (9) definierten Tensor zweiten Ranges gelten, am ein­fachsten dadurch beweisen, dass man sie für spezielle Tensoren vom Typus (8) darstellt.

Kontravarianter Tensor beliebigen Ranges. Nach Einsteins Worten sei es klar, dass man entspre­chend (8) und (9) auch kontra­variante Tensoren dritten und höheren Ranges definieren kann mit 4³ usw. Kompo­nenten. Ebenso ersicht­lich sei aus (8) und (9), dass man in diesem Sinne den kontra­varianten Vierer­vektor als kontra­varianten Tensor ersten Ranges auf­fassen kann.

Kovarianter Tensor. Bildet man anderer­seits die 16 Produkte A_μν der Kompo­nenten zweier kovarianter Vierer­vektoren A_μ und B_ν: (10)

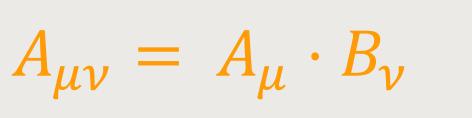
so gilt für diese folgendes Trans­formations­gesetz: (11)

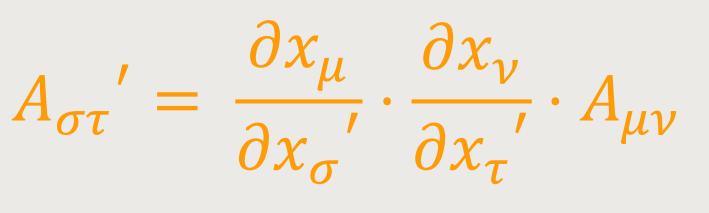
Durch dieses Trans­formations­gesetz wird der kovariante Tensor zweiten Ranges definiert. Alle Bemer­kungen, die zuvor über die kontra­varianten Tensoren gemacht wurden, gelten auch für die kovarianten Tensoren.

Bemerkung: Es sei laut Einstein bequem, den Skalar (Invariante) sowohl als kontra­varianten wie als kovarianten Tensor vom Range Null zu behandeln.

Gemischter Tensor. Man kann auch einen Tensor zweiten Ranges vom Typus (12)

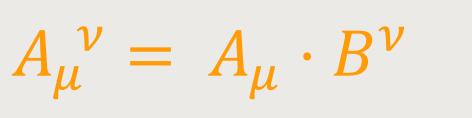
definieren, der bezüg­lich des Index μ kovariant, aber bezüg­lich des Index ν kontra­variant ist. Dessen Trans­formations­gesetz lautet: (13)

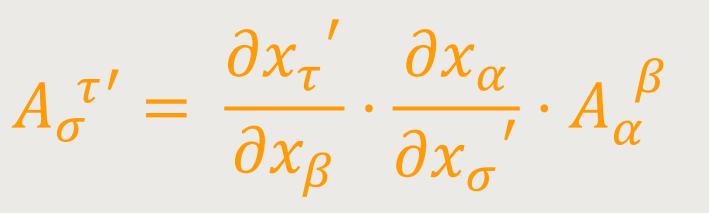
Natürlich gibt es gemischte Tensoren mit beliebig vielen Indizes kovarianten und beliebig vielen Indizes kontra­varianten Charakters. In diesem Fall können der kovariante und der kontra­variante Tensor als spezielle Fälle des gemischten angesehen werden.

Symmetrische Tensoren. Ein kontra­varianter bzw. kovarianter Tensor zweiten oder höheren Ranges heißt „symmetrisch”, wenn zwei Kompo­nenten, die durch Ver­tauschung irgend­welcher zweier Indizes aus­einander hervor­gehen, gleich sind. Der Tensor A^μν bzw. A_μν ist also symmetrisch, wenn für jede Kombi­nation der Indizes: (14)

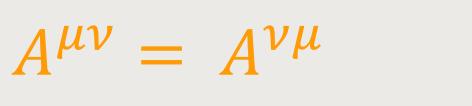
bzw.: (14a)

ist.

Laut Einstein müsste bewiesen werden, dass die so definierte Symmetrie eine vom Bezugs­system unab­hängige Eigen­schaft ist. Aus (9) folgt in der Tat mit Rück­sicht auf (14):

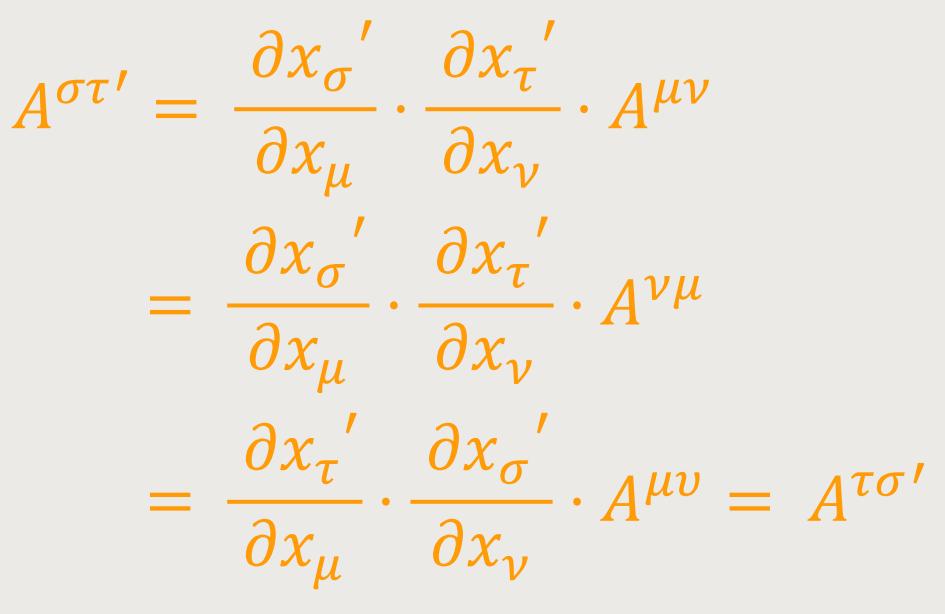
Die vorletzte Gleichung beruht auf der Ver­tauschung der Summen­indizes μ und ν (das heißt lediglich auf Änderung der Bezeichnungs­weise).

Antisymmetrische Tensoren. Ein kontra­varianter bzw. kovarianter Tensor zweiten, dritten und vierten Ranges heißt anti­symmetrisch, wenn zwei Kompo­nenten, die durch Ver­tauschung irgend­welcher zweier Indizes aus­einander hervor­gehen, entgegen­gesetzt gleich sind. Der Tensor A^μν bzw. A_μν ist also anti­symmetrisch, wenn stets: (15)

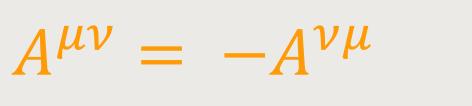
bzw.: (15a)

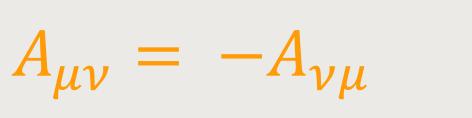
ist.

Von den 16 Komponenten A^μν ver­schwinden die vier Kompo­nenten A^μμ. Die übrigen sind paar­weise entgegen­gesetzt gleich, so dass nur 6 numerisch verschie­dene Kompo­nenten vor­handen sind (Sechservektor). Ebenso sieht man, dass der anti­symmetrische Tensor A^μνσ (dritten Ranges) nur vier numerisch ver­schiedene Kompo­nenten hat, dagegen der anti­symmetrische Tensor A^μνστ nur eine einzige. Symmetrische Tensoren höheren als den des vierten Ranges gibt es in einem Kontinuum von vier Dimensionen nicht.

§ 7. Multiplikation der Tensoren.

Äußere Multi­plikation der Tensoren. Man erhält aus den Kompo­nenten eines Tensors vom Range z und eines solchen vom Range z' die Kompo­nenten eines Tensors vom Range z + z', indem man alle Kompo­nenten des ersten mit allen Kompo­nenten des zweiten paar­weise multi­pliziert. So entstehen beispiels­weise die Tensoren T aus den Tensoren A und B verschie­dener Art.

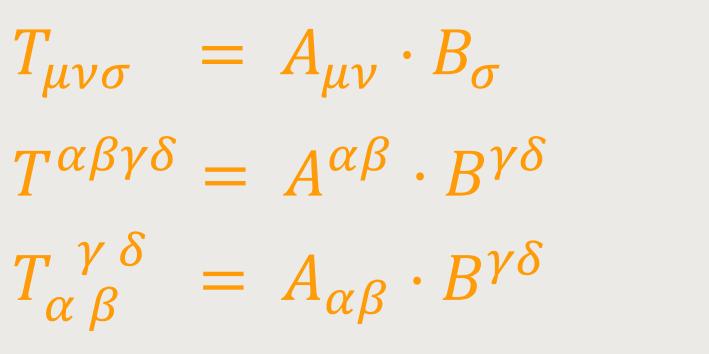
Der Beweis des Tensor­charakters der Tensoren T ergibt sich unmittel­bar aus den Dar­stellungen (8), (10), (12) oder aus den Trans­formations­regeln (9), (11), (13). Die Gleichungen (8), (10), (12) sind selbst Beispiele äußerer Multi­plikation (von Tensoren ersten Ranges).

„Verjüngung” eines gemischten Tensors. Aus jedem gemisch­ten Tensor kann ein Tensor von einem um zwei kleineren Range gebildet werden, indem man einen Index kovarianten und einen Index kontra­varianten Charakters gleich­setzt und nach diesem Index summiert („Verjüngung”). Man gewinnt so z.B. aus dem gemischten Tensor vierten Ranges A_α^γ_β^δ den gemischten Tensor zweiten Ranges:

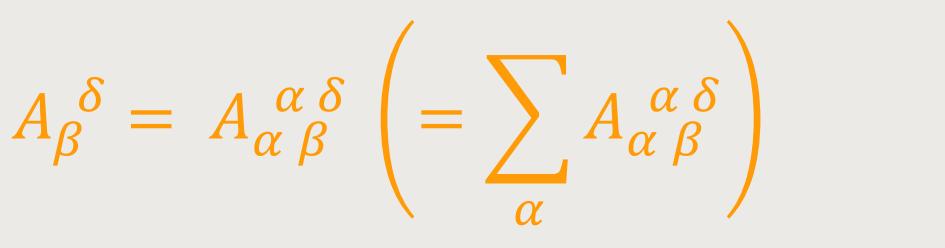
Und aus diesem, durch noch­malige Verjüngung, den Tensor nullten Ranges:

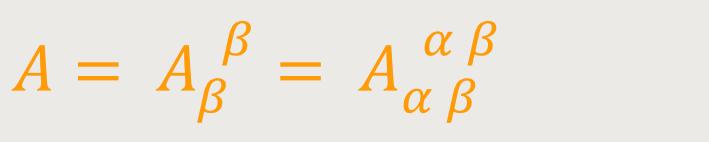
Der Beweis dafür, dass das Ergebnis der Verjüngung wirklich Tensor­charakter besitzt, ergibt sich entweder aus der Tensor­darstellung gemäß der Verall­gemeinerung von (12) in Ver­bindung mit (6) oder aus der Verall­gemeinerung von (13).

Innere und gemischte Multi­plikation der Tensoren. Diese bestehen in der Kombi­nation der äußeren Multi­plikation mit der Verjüngung.

Beispiele:

Aus dem kovarianten Tensor zweiten Ranges A_μν und dem kontra­varianten Tensor ersten Ranges B^σ bildet man durch äußere Multi­plikation den gemischten Tensor

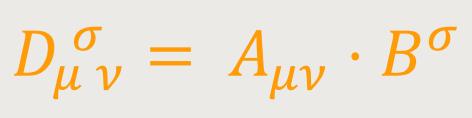
Durch Verjüngung nach den Indizes ν, σ entsteht der kovariante Vierer­vektor

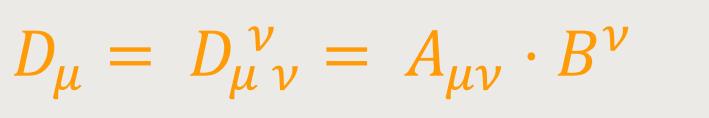
Diesen bezeichnet man auch als inneres Produkt der Tensoren A_μν und B^σ. Analog bildet man aus den Tensoren A_μν und B^στ durch äußere Multi­plikation und zweimalige Verjüngung das innere Produkt A_μν B^μν. Durch äußere Produkt­bildung und einmalige Verjüngung erhält man aus A_μν und B^στ den gemischten Tensor zweiten Ranges

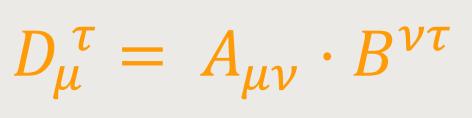
Man kann diese Operation treffend als eine gemischte bezeich­nen. Denn sie ist eine äußere Produkt­bildung bezüg­lich der Indizes ν und σ.

Einstein beabsichtigte nun einen Satz zu beweisen, der zum Nachweis des Tensor­charakters oft verwendbar ist. Nach dem zuvor Dar­gelegten ist A_μν B^μν ein Skalar, wenn A_μν und B^στ Tensoren sind. Einstein behauptete auch folgendes: Wenn A_μν B^μν für jede Wahl des Tensors B^μν eine Invariante ist, so hat A_μν Tensor­charakter.

Beweis: Es ergibt sich nach Voraus­setzung für eine beliebige Substitution:

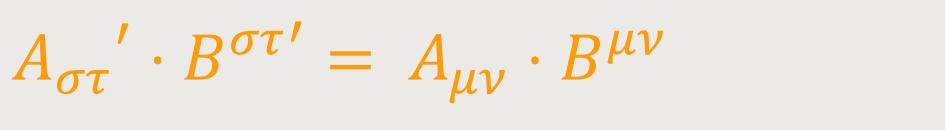
Nach der Umkehrung von (9) ist aber

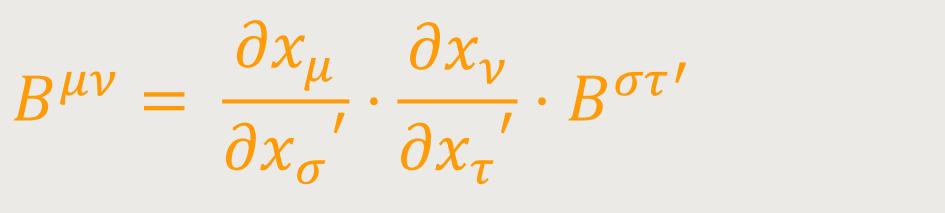
Wird dies in obige Gleichung ein­gesetzt, folgt daraus:

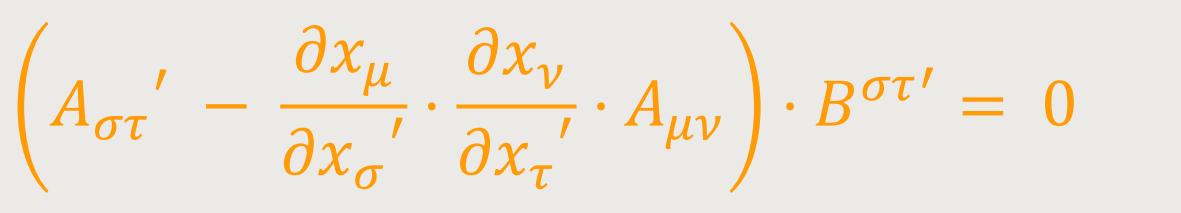
Dies kann bei beliebiger Wahl von B^στ' nur dann erfüllt sein, wenn die Klammer ver­schwindet, woraus mit Rück­sicht auf (11) obige Behauptung folgt.

Dieser Satz gilt entspre­chend für Tensoren beliebigen Ranges und Charakters. Der Beweis ist stets analog zu führen.

Der Satz lässt sich ebenso beweisen in der Form: Sind B^μ und C^ν beliebige Vektoren, und ist bei jeder Wahl derselben das innere Produkt

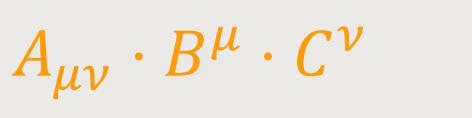
ein Skalar, so ist A_μν ein kovarianter Tensor. Dieser letzte Satz gilt auch dann noch, wenn nur die spezielle Aussage zutrifft, dass bei beliebiger Wahl des Vierer­vektors B^μ das skalare Produkt

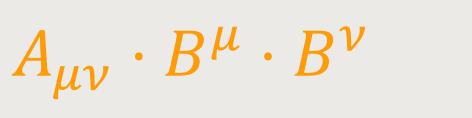
ein Skalar ist, falls zudem bekannt ist, dass A_μν der Symmetrie­bedingung A_μν = A_νμ genügt. Denn auf zuvor beschrie­bene Weise beweist man den Tensor­charakter von (A_μν + A_νμ ), woraus dann wegen der Symmetrie­eigenschaft der Tensor­charakter von A_μν selbst folgt. Auch dieser Satz lässt sich leicht verall­gemeinern auf den Fall kovarianter und kontra­varianter Tensoren beliebigen Ranges.

Nach Einsteins Worten folgt endlich aus dem Bewiesenen der ebenfalls auf beliebige Tensoren zu verall­gemeinernde Satz: Wenn die Größen A_μν B^ν bei beliebiger Wahl des Vierer­vektors B^ν einen Tensor ersten Ranges bilden, so ist A_μν ein Tensor zweiten Ranges. Ist nämlich C^μ ein beliebiger Vierer­vektor, so ist wegen des Tensor­charakters A_μν B^ν das innere Produkt A_μν C^μ B^ν bei beliebiger Wahl der beiden Vierer­vektoren C^μ und B^ν ein Skalar, woraus vorherige Behauptung folgt.

§ 8. Einiges über den Fundamental­tensor der g_μν

Der kovariante Fundamental­tensor. In dem invarianten Ausdruck des Quadrats des Linienelements

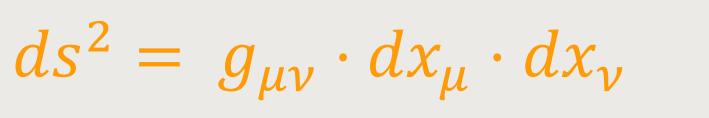
spielt dx_μ die Rolle eines beliebig wähl­baren kontra­varianten Vektors. Da ferner g_μν = g_νμ ent­spricht, folgt daraus nach den Betrach­tungen des letzten Paragraphen, dass g_μν ein kovarianter Tensor zweiten Ranges ist. Er wird bezeichnet als „Fundamental­tensor”. Im Folgenden beabsichtigte Einstein einige Eigen­schaften dieses Tensors abzu­leiten, die zwar auf jeden Tensor zweiten Ranges zutreffen. Aber die besondere Rolle des Fundamental­tensors bei der Relativi­täts­theorie bringt es mit sich, dass die zu ent­wickelnden Relationen nur bei dem Fundamental­tensor von Bedeutung sind. Einstein schreibt ihren physika­lischen Grund der Besonder­heit der Gravitations­wirkungen zu.

Der kontravariante Fundamental­tensor. Bildet man in dem Deter­minanten­schema der g_μν zu jedem g_μν die Unter­deter­minante und dividiert diese durch die Deter­minante g = |g_μν| der g_μν, so erhält man gewisse Größen g^μν (= g^νμ), von denen Einstein beweisen wollte, dass sie einen kontra­varianten Tensor bilden.

Nach einem bekannten Deter­minanten­satz lautet: (16)

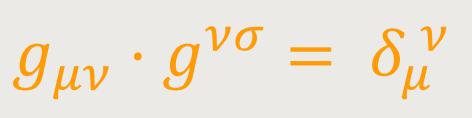
Wobei das Zeichen δ_μ^ν ent­weder 1 oder 0 bedeutet, je nach­dem ob μ = ν oder μ ν ent­spricht. Statt des obigen Aus­drucks für ds² kann man auch schreiben:

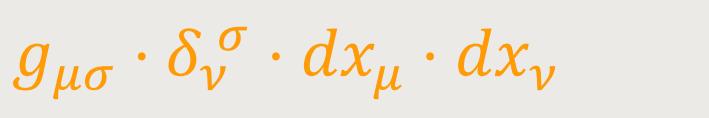
oder nach (16):

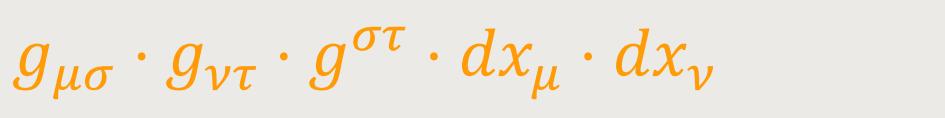
Nun bilden aber nach den Multi­plika­tions­regeln des vorigen Para­graphen die Größen

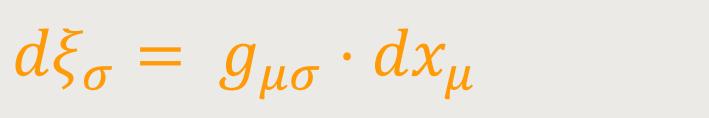
einen kovarianten Vierer­vektor, und zwar (wegen der will­kürlichen Wähl­bar­keit der dx_μ) einen beliebig wähl­baren Vierer­vektor. Indem man ihn in obigen Aus­druck des Quadrats ein­führt, erhält man:

Da dies bei beliebiger Wahl des Vektors dζ_σ ein Skalar ist, und g^στ nach seiner Definition in den Indizes σ und τ symmetrisch ist, folgt aus den Ergeb­nissen des vor­herigen Para­graphen, dass g^στ ein kontra­varianter Tensor ist. Aus (16) folgt anderer­seits, dass auch δ_μ^ν ein Tensor ist, der sich als gemischter Fundamental­tensor bezeichnen lässt.

Determinante des Fundamental­tensors. Nach dem Multi­plikations­satz der Deter­minanten ist

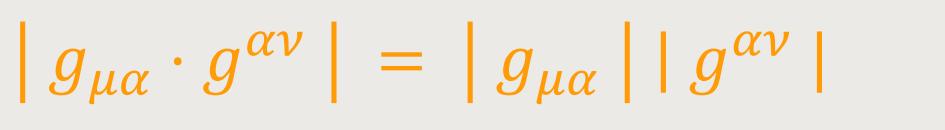
Anderseits ist

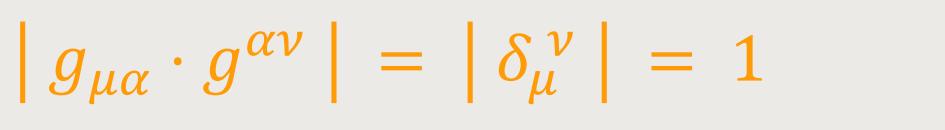
Also folgt: (17)

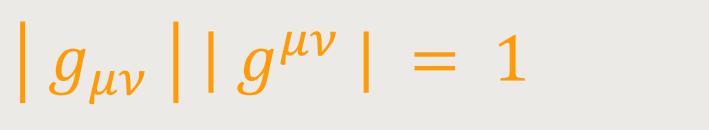
Invariante des Volumens. Zuerst wird das Trans­formations­gesetz der Deter­minante g = |g_μν| gesucht. Gemäß (11) ergibt sich:

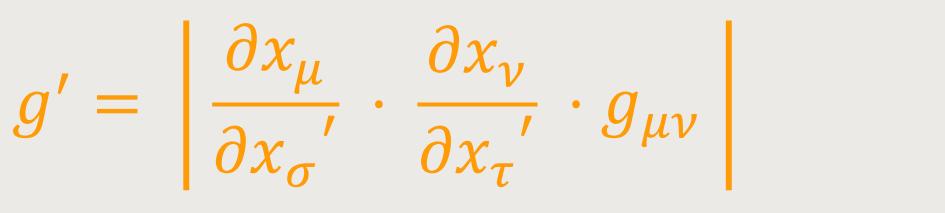
Hieraus folgt durch zweimalige Anwendung des Multi­plikations­satzes der Deter­mination:

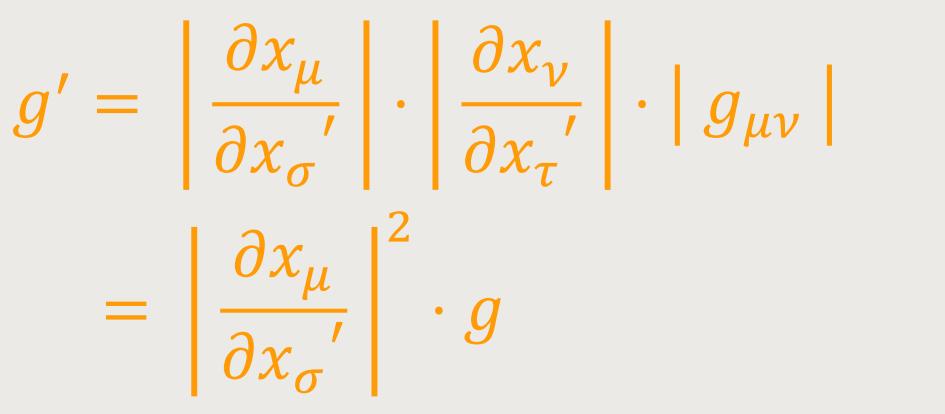
oder

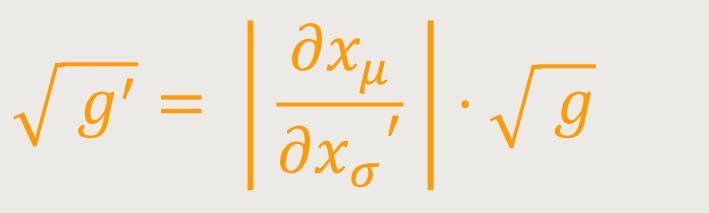
Andererseits lautet das Gesetz der Trans­formation des Volumen­elements:

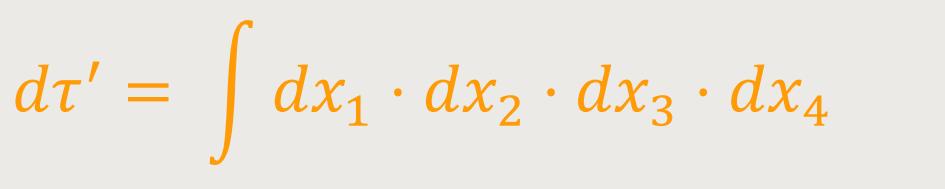
Bzw. nach dem bekannten Jakobischen Satz:

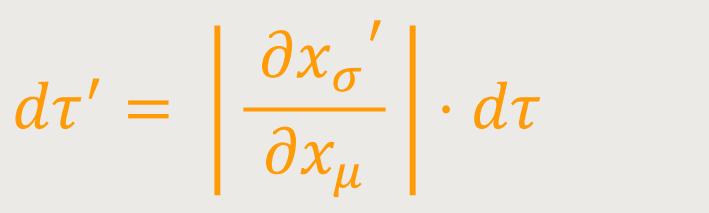
Durch Multiplikation der beiden letzten Gleichungen erhält man: (18)

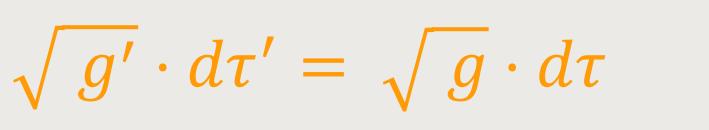
Statt √g wird im Folgenden die Größe √−g ein­geführt, welche wegen des hyper­bolischen Charakters des raum­zeit­lichen Konti­nuums stets einen reellen Wert hat. Die Invariante √(−g) · dτ ist gleich der Größe des im „örtlichen Bezugs­system” mit starren Maßstäben und Uhren im Sinne der Speziellen Relativi­täts­theorie gemessenen 4-dimen­sionalen Volumen­elements.

Bemerkung über den Charakter des raum­zeitlichen Kontinuums. Die Voraus­setzung, dass im unendlich Kleinen stets die Spezielle Relativi­täts­theorie gilt, bringt es mit sich, dass sich ds² immer gemäß (1) durch die reellen Größen dX₁ ... dX₄ ausdrücken lässt. Bezeichnet man dτ₀ das „natürliche” Volumen­element dX₁ dX₂ dX₃ dX₄, so ist also: (18a)

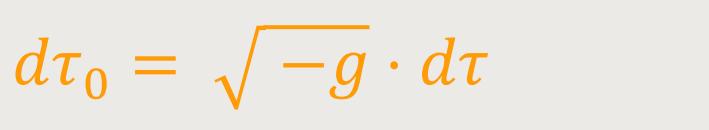
Soll an einer Stelle des 4-dimen­sionalen Kontinuums √−g ver­schwinden, so bedeutet dies, dass hier einem endlichen Koordi­naten­volumen ein unendlich kleines „natürliches” Volumen entsprechen würde. Dies möge nach Einsteins Ansicht nirgends der Fall sein. Dann kann g sein Vorzeichen nicht ändern. Einstein setzte im Sinne der Speziellen Relativi­täts­theorie voraus, dass g stets einen endlichen negativen Wert habe. Es sei dies eine Hypothese über die physika­lische Natur des betrach­teten Kontinuums und gleich­zeitig eine Fest­setzung über die Koordinaten­wahl.

Ist aber −g stets positiv und endlich, so liegt es nahe, die Koordinaten­wahl a posteriori bzw. auf Basis der Erfahrung so zu treffen, dass diese Größe gleich 1 wird. Nach Einsteins Worten würde sich später zeigen, dass durch eine solche Beschrän­kung der Koordi­naten­wahl eine bedeutende Verein­fachung der Natur­gesetze erzielt werden kann. An Stelle von (18) tritt dann einfach:

Woraus mit Rücksicht auf den Jakobischen Satz folgt: (19)

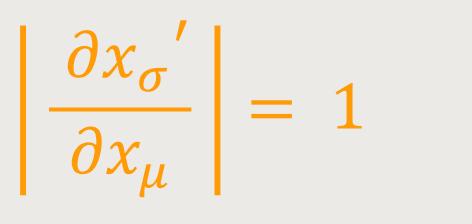
Bei dieser Koordinaten­wahl sind also nur Substitu­tionen der Koordinaten von der Deter­minante 1 zulässig.

Es wäre aber irrtümlich, zu glauben, dass dieser Schritt einen partiellen Verzicht auf das all­gemeine Relativi­täts­postulat bedeuten würde. Es stellt sich nicht die Frage: „Wie heißen die Natur­gesetze, welche gegen­über allen Trans­forma­tionen von der Deter­minante 1 kovariant sind?” Sondern es erhebt sich die Frage: „Wie heißen die all­gemein kovarianten Natur­gesetze?” Erst nach­dem Einstein diese auf­gestellt hätte, wollte er ihren Ausdruck durch eine besondere Wahl des Bezugs­systems verein­fachen.

Bildung neuer Tensoren mithilfe des Fundamental­tensors. Durch innere, äußere und gemischte Multi­plikation eines Tensors mit dem Fundamental­tensor entstehen Tensoren anderen Charakters und Ranges.

Beispiele:

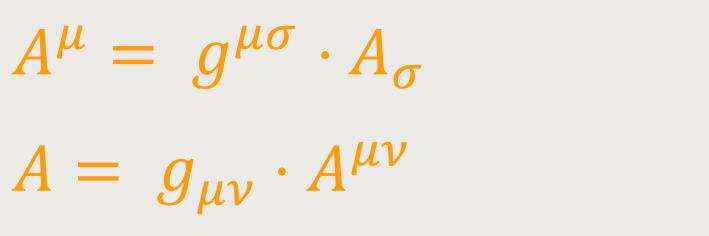
Besonders sei auf folgende Bildungen hingewiesen:

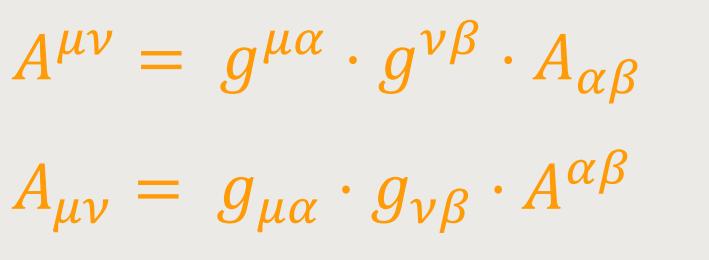
(„Ergänzung” des kovarianten bzw. kontravarianten Tensors) und

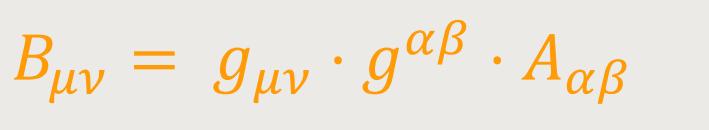
Man bezeichnet B_μν den zu A_μν gehörigen reduzierten Tensor. Analog:

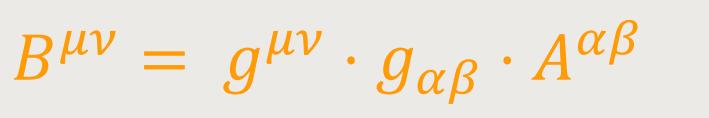
Es sei bemerkt, dass g^μν nichts anderes ist, als die Ergänzung von g_μν. Denn man hat

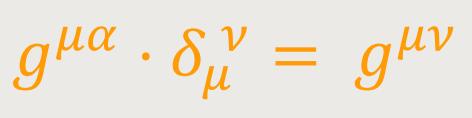
§ 9. Gleichung der geodätischen Linie (bzw. der Punktbewegung).

Hinweis: In der Mathematik verwendet man den Begriff „geodätisch” für die theoretisch kürzeste Ver­bindung zwischen zwei Punkten auf gekrümmten Flächen − die geodätische Linie, welche auf der Erd­kugel einer Orthodrome entspricht.

Da das „Linien­element” ds eine unabhängig vom Koordi­naten­system definierte Größe ist, hat auch die zwischen zwei Punkten P₁ und P₂ des 4-dimen­sionalen Kontinuums gezogene Linie, für welche ∫ ds ein Extremum ist (geodätische Linie), eine von der Koordi­naten­wahl unabhängige Bedeutung. Ihre Gleichung lautet: (20)

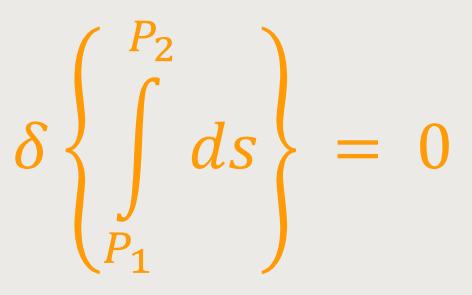
Aus dieser Gleichung findet man in bekannter Weise durch Aus­führung der Variation vier absolute Differential­gleichungen, welche diese geodätische Linie bestimmen. Diese Ableitung führte Einstein der Voll­ständigkeit hier mit auf. Es sei λ eine Funktion der Koordinaten x_ν. Diese definiert eine Schar von Flächen, welche die gesuchte geodätische Linie sowie alle ihr unendlich benach­barten, durch die Punkte P₁ und P₂ gezo­genen Linien schneiden. Jede solche Kurve kann dann dadurch gegeben werden, dass ihre Koordinaten x_ν in Funktion von λ ausge­drückt werden. Das Zeichen δ soll dabei dem Über­gang von einem Punkt der gesuchten geodätischen Linie zu dem­jenigen Punkt einer benach­barten Kurve entsprechen, welcher zu dem erwähnten λ gehört. Dann lässt sich (20) ersetzen durch: (20a)

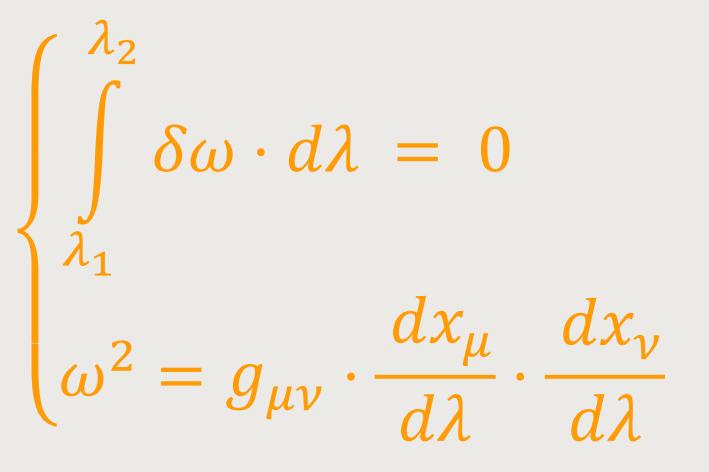
Da aber

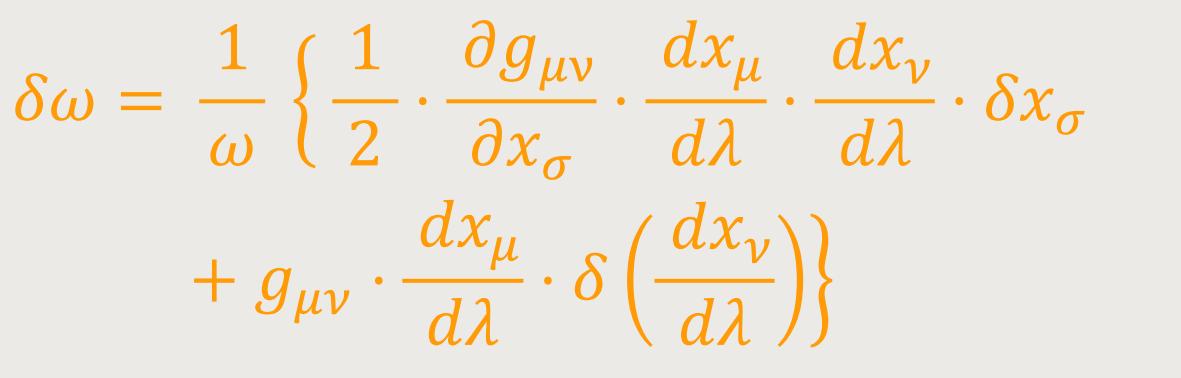
so erhält man nach Einsetzen von δ ω in (20a) mit Rück­sicht darauf, dass

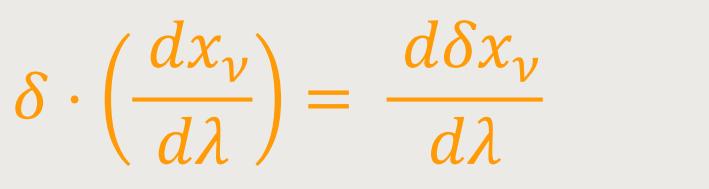
wobei sich nach partieller Integration ergibt: (20b)

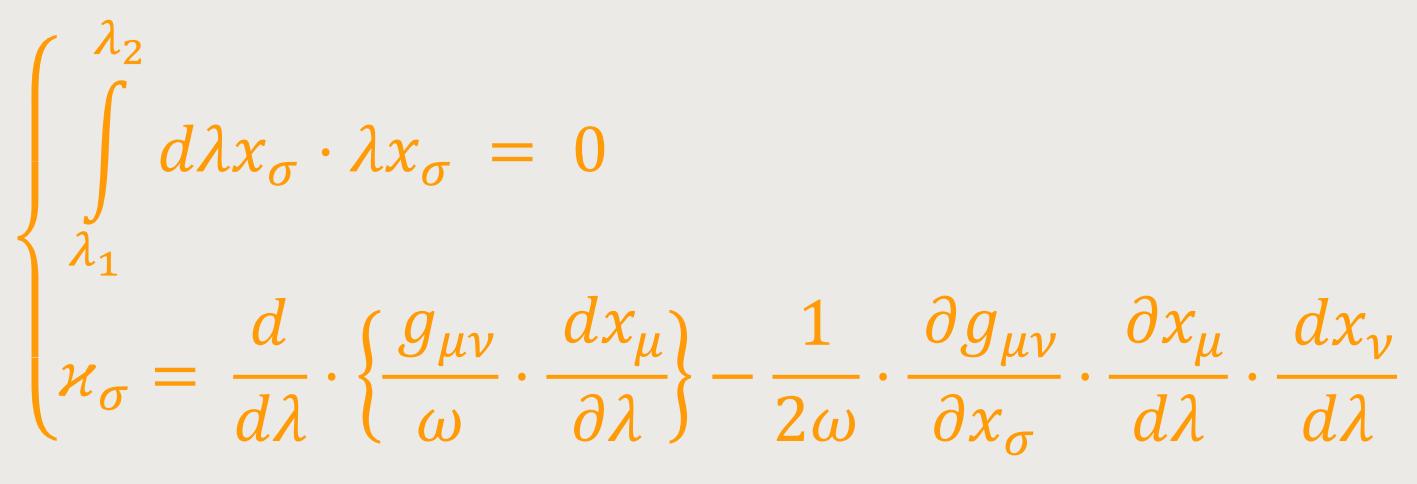
Hieraus folgt wegen der freien Wähl­bar­keit der δx _σ das Ver­schwinden der ϰ_σ. Also sind: (20c)

die Gleichungen der geodätischen Linie. Ist auf der betrach­teten geodätischen Linie nicht ds = 0, so können wir als Parameter λ die auf der geodätischen Linie gemessene Bogen­länge s wählen. Dann wird ω = 1, und man erhält an Stelle von (20c):

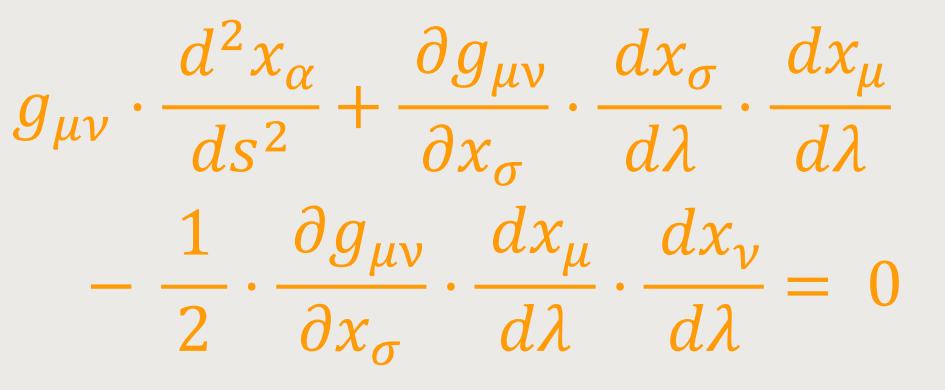
oder durch bloße Änderung der Bezeichnungs­weise ergibt sich: (20d)

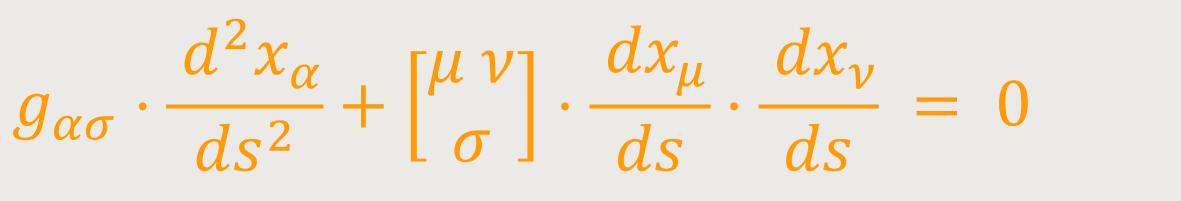
Wobei nach Christoffel festgelegt ist: (21)

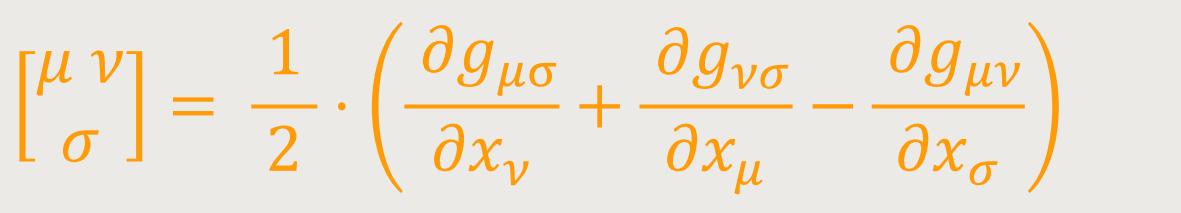
Multipliziert man schließlich (20d) mit g^στ (äußere Multi­plika­tion bezüglich τ, innere bezüglich σ, so erhält man schließlich als endgütige Form der Gleichung der geodätischen Linie: (22)

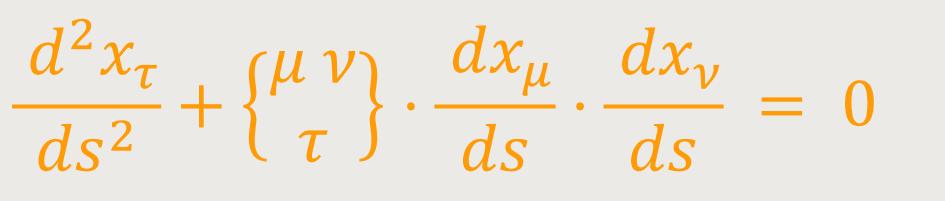
Hierbei ist nach Christoffel fest­gelegt: (23)

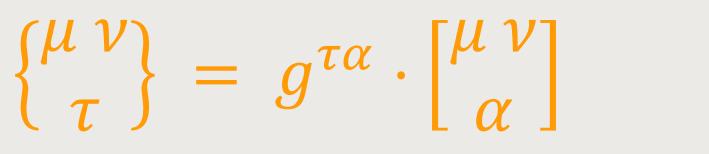
⇦ Kapitel Kapitel ⇨