§ 10. Die Bildung von Tensoren durch Differentiation

Gestützt auf die Gleichung der geodä­tischen Linie lassen sich leicht die Gesetze ableiten, nach welchen durch Differen­tiation aus Tensoren neue Tensoren gebildet werden können. Dadurch wird man erst in die Lage versetzt, all­gemein kovariante Differential­gleichungen aufzu­stellen. Man erreicht dieses Ziel durch wieder­holte Anwendung des nach­folgenden einfachen Satzes.

Ist in unserem Kontinuum eine Kurve gegeben, deren Punkte durch die Bogen­distanz s von einem Fix­punkt auf der Kurve charakte­risiert sind, und ist ferner φ eine invariante Raum­funktion, so ist auch dφ/ds eine Invariante. Der Beweis liegt darin, dass sowohl dφ als auch ds Invariante sind.

Da

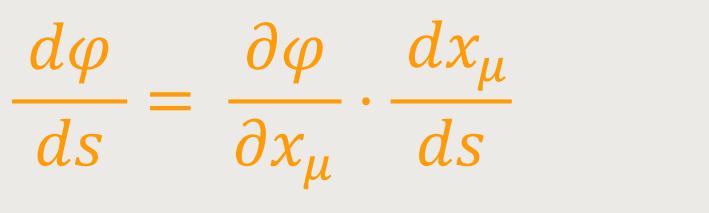
so ist auch

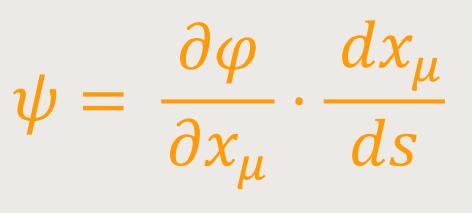
eine Invariante, und zwar für alle Kurven, die von einem Punkt des Kontinuums ausgehen, das heißt für beliebige Wahl des Vektors der dx_μ. Daraus folgt unmittel­bar, dass: (24)

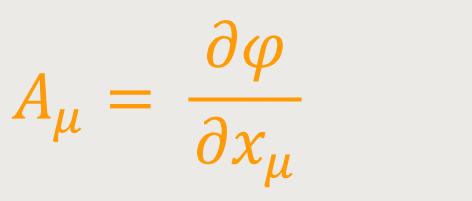
ein kovarianter Vierer­vektor ist (Gradient von φ).

Nach diesem Satz ist ebenso der auf einer Kurve genommene Differential­quotient

eine Invariante. Durch Einsetzten von ψ erhält man zunächst:

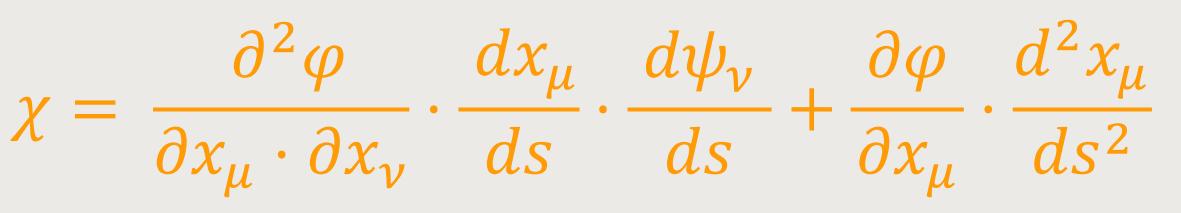
Hieraus lässt sich zunächst die Existenz eines Tensors nicht ableiten. Legt man nun aber fest, dass die Kurve, auf welcher differenziert wurde, eine geodä­tische Kurve sei, so erhält man nach (22) durch Ein­setzen von d²x_ν /ds²:

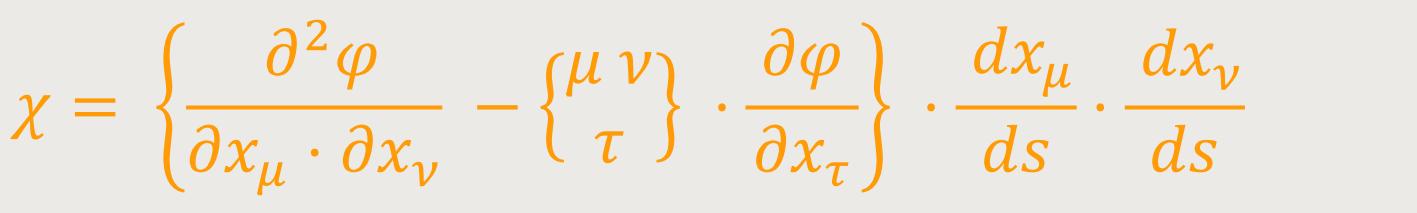
Aus der Vertausch­barkeit der Differen­tiationen nach μ und ν und daraus, dass gemäß (23) und (21) die Klammer { ^μτ^ν } bezüglich μ und ν symmetrisch ist, folgt, dass der Klammer­ausdruck in μ und ν symmetrisch ist. Da man von einem Punkt des Kontinuums aus in beliebiger Richtung eine geodä­tische Linie ziehen kann, dx_ν /ds also ein Vierer­vektor mit frei wähl­barem Verhältnis der Komponenten ist, folgt nach den Ergebnissen des §7, dass: (25)

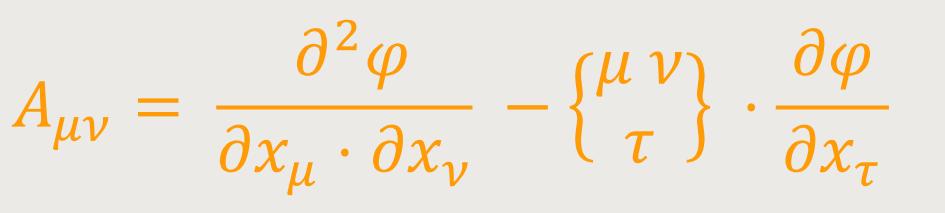
ein kovarianter Tensor zweiten Ranges ist. Als Ergebnis lässt sich sagen: Aus dem kovarianten Tensor ersten Ranges

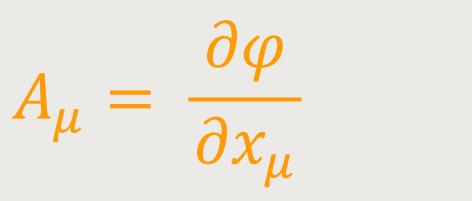
kann durch Differen­tiation ein kovarianter Tensor zweiten Ranges gebildet werden: (26)

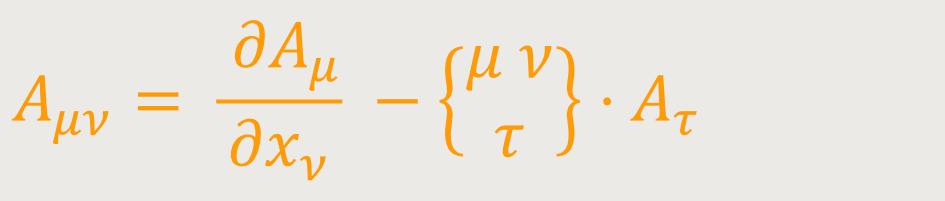
Man bezeichnet den Tensor A_μν als die „Erweiterung” des Tensors A_μ. Nach Einsteins Worten lässt sich zunächst leicht zeigen, dass diese Umformung auch dann auf einen Tensor führt, wenn der Vektor A_μ nicht als ein Gradient dar­stellbar ist. Um dies nachzu­vollziehen, sei zunächst erwähnt, dass

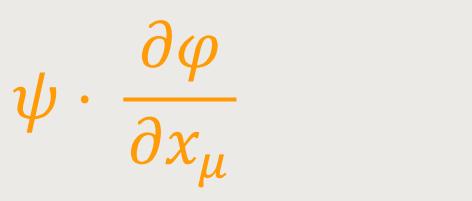
ein kovarianter Vierer­vektor ist, wobei ψ und φ Skalare sind. Dies ist auch der Fall für eine aus vier solchen Gliedern bestehende Summe

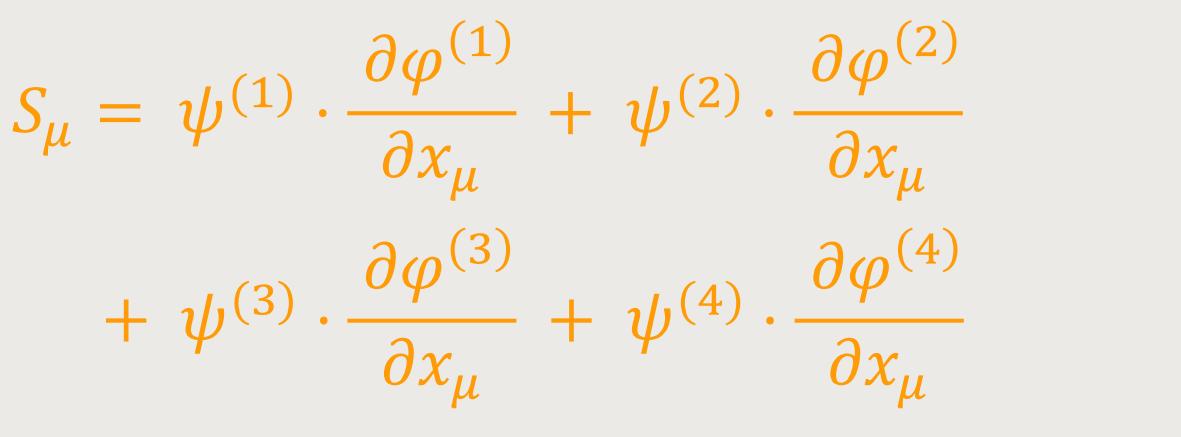
falls ψ⁽¹⁾ φ⁽¹⁾ ... ψ⁽⁴⁾ φ⁽⁴⁾ Skalare sind. Nun ist aber klar, dass sich jeder kovariante Vierer­vektor in der Form S_μ darstellen lässt. Ist nämlich A_μ ein Vierer­vektor, dessen Komponenten beliebig gegebene Funktionen der x_ν sind, so hat man nur in Anhängigkeit des gewählten Koordinaten­systems festzulegen

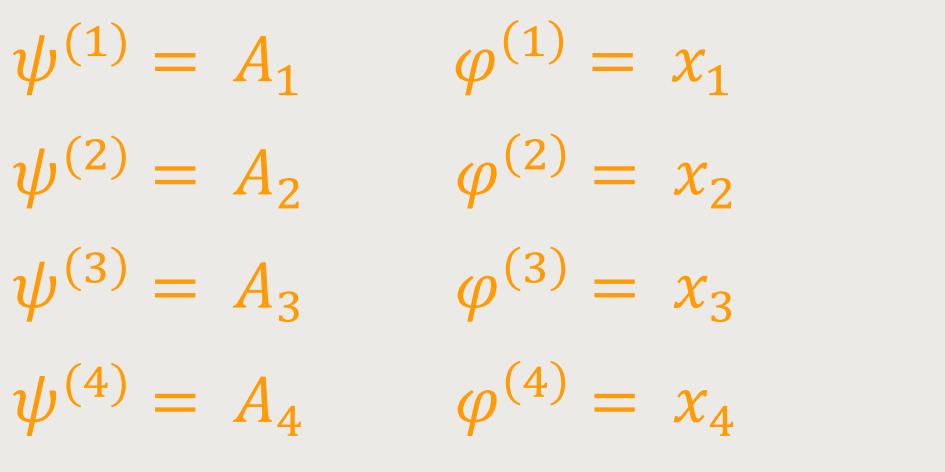
um zu erreichen, dass S_μ gleich A_μ wird.

Um daher zu beweisen, dass A_μν ein Tensor ist, wenn auf der rechten Seite für A_μ ein beliebiger kovarianter Vierer­vektor ein­gesetzt wird, braucht man nur zu zeigen, dass dies für den Vierer­vektor S_μ zutrifft. Für Letzteres ist es aber, wie ein Blick auf die rechte Seite von (26) zeigt, hin­reichend, den Nach­weis für den Fall

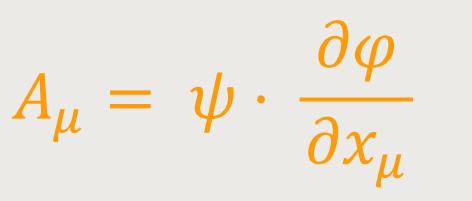
zu führen. Es hat nun die mit ψ multi­plizierte rechte Seite von (25) Tensor­charakter:

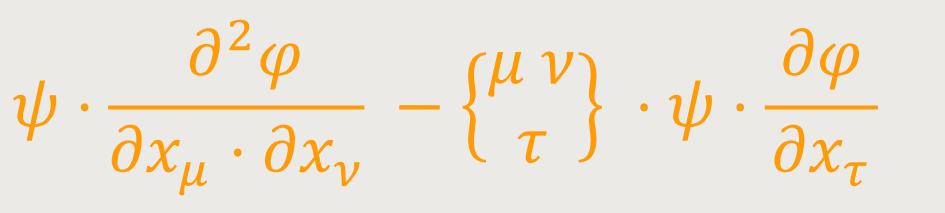
Ebenso ist

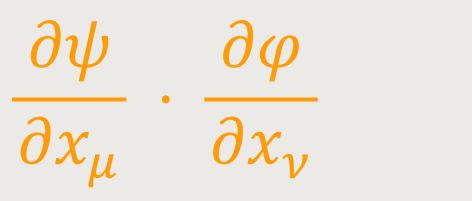
ein Tensor (äußeres Produkt zweier Vierer­vektoren). Durch Addition folgt der Tensor­charakter von

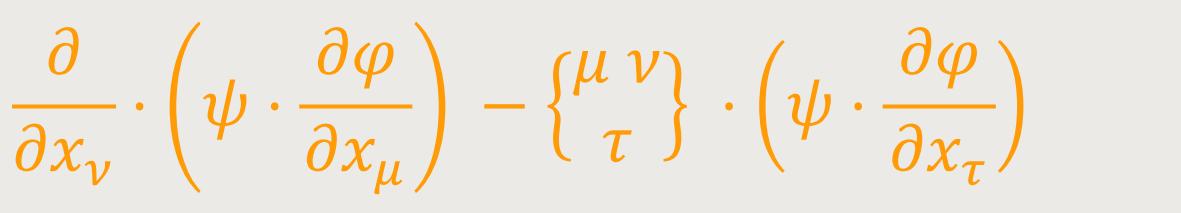
Damit ist, wie ein erneuter Blick auf (26) zeigt, der verlangte Nach­weis für den Vierer­vektor

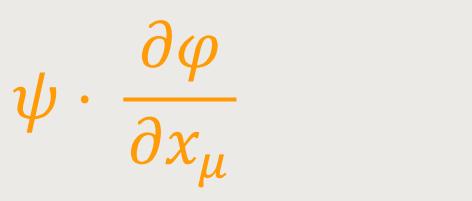
und daher nach dem zuvor Bewiesenen für jeden beliebigen Vierer­vektor A_μ geführt.

Mit Hilfe der Erweiterung des Vierer­vektors kann man leicht die „Erweiterung” eines kovarianten Tensors beliebigen Ranges definieren. Diese Umformung ist eine Verall­gemeinerung der Erweiterung des Vierer­vektors. Einstein beschränkte sich dabei auf die Auf­stellung der Erweiterung des Tensors zweiten Ranges, da dieser das Bildungs­gesetz bereits klar erkennen lässt.

Wie bereits erwähnt, lässt sich jeder kovariante Tensor zweiten Ranges dar­stellen als eine Summe von Tensoren vom Typus A_μ B_ν.
An dieser Stelle ergänzt Einstein: Durch äußere Multi­plikation der Vektoren mit den (beliebig gegebenen) Komponenten A₁₁, A₁₂, A₁₃, A₁₄ bzw. 1, 0, 0, 0 entsteht ein Tensor mit den Kompo­nenten

Durch Addition von vier Tensoren von diesem Typ erhält man den Tensor A_μν mit beliebig vor­geschrie­benen Kompo­nenten.

Nach Einsteins Worten würde es deshalb genügen, den Aus­druck der Erweiterung für einen solchen speziellen Tensor abzu­leiten. Gemäß (26) haben nach­folgende Aus­drücke Tensor­charakter:

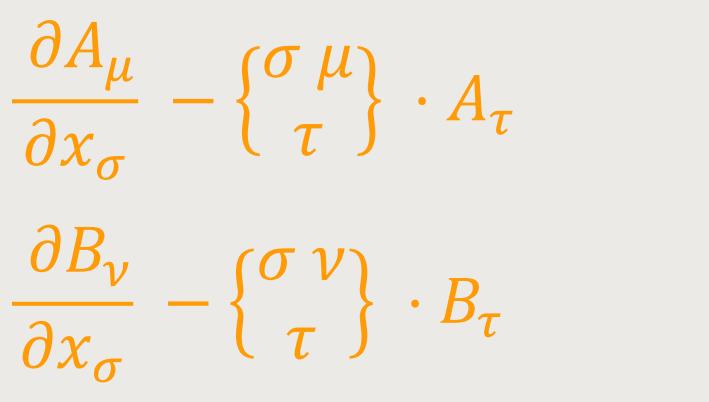
Durch äußere Multi­plikation des ersten mit B_ν und des zweiten mit A_μ erhält man je einen Tensor dritten Ranges. Deren Addition ergibt den Tensor dritten Ranges, wobei A_μν = A_μ B_ν gesetzt ist: (27)

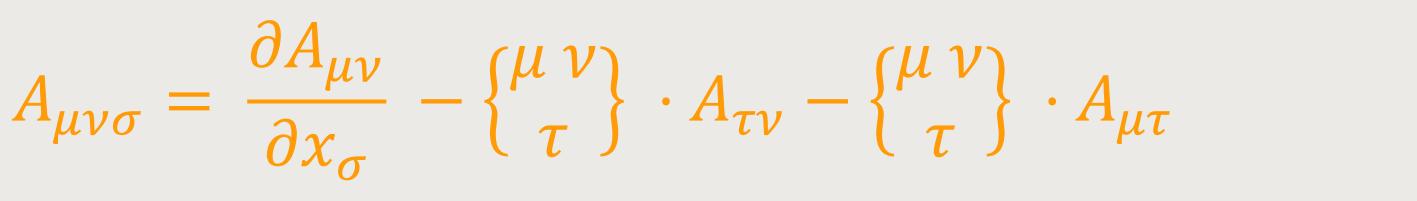
Da die rechte Seite von (27) linear und homogen bezüg­lich der A_μν und deren ersten Ableitungen ist, führt dieses Bildungs­gesetz nicht nur bei einem Tensor vom Typus A_μ B_ν zu einem Tensor, sondern auch bei einer Summe solcher Tensoren, das heißt bei einem beliebigen kovarianten Tensor zweiten Ranges. Daher nennt man A_μνσ auch die Erweiterung des Tensors A_μν.

Es sei erwähnt, dass (26) und (24) nur spezielle Fälle von (27) sind (hier die Erweiterung des Tensors ersten bzw. nullten Ranges). Grundsätzlich lassen sich alle speziellen Bildungs­gesetze von Tensoren in Bezug auf (27) in Verbindung mit Tensor­multi­plika­tionen auffassen.

§ 11. Einige Spezialfälle von besonderer Bedeutung.

Einige den Fundamental­tensor betreffende Hilfs­sätze. Einstein leitete auch hier im Nach­folgenden zunächst einige viel gebrauchte Hilfs­gleichungen ab. Nach der Regel von der Differen­tiation der Deter­minanten ist: (28)

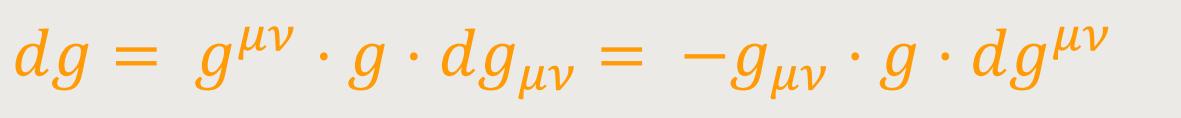
Die letzte Form recht­fertigt sich durch die vorletzte, wenn man bedenkt, dass

woraus folgt, dass:

Aus (28) folgt: (29)

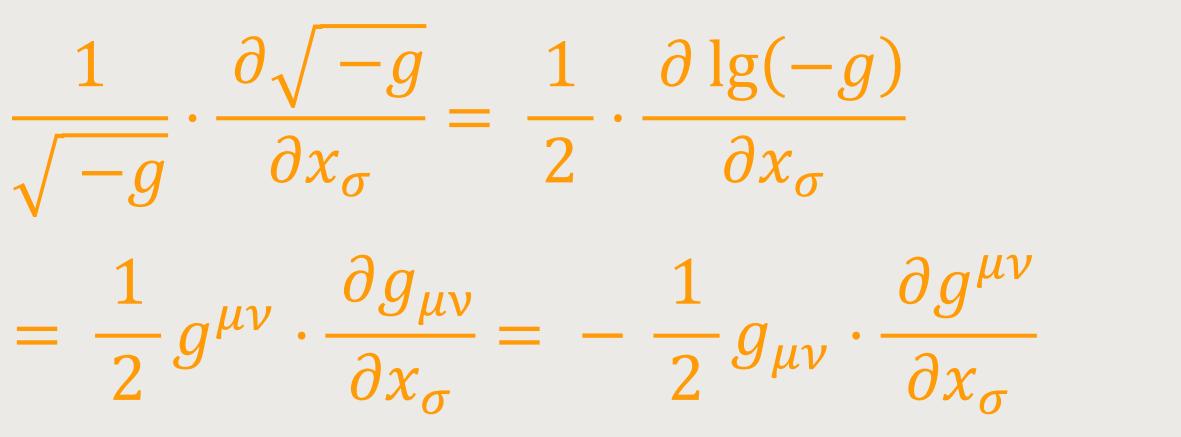
Aus

folgt ferner durch Differen­tiation: (30)

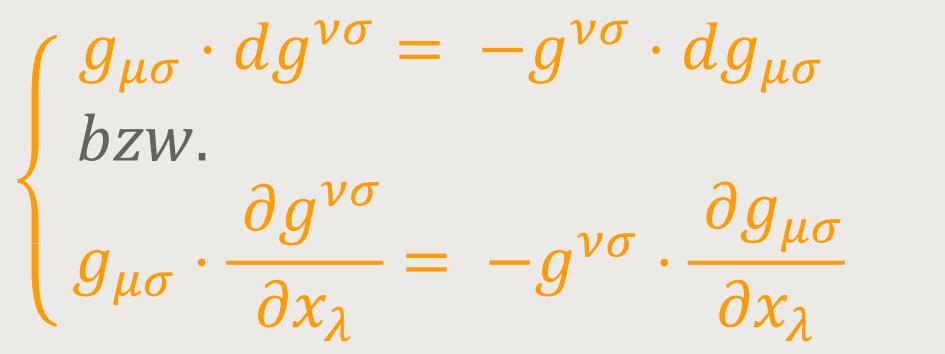
Durch gemischte Multipli­kation mit g^στ bzw. g_νλ erhält man hieraus (bei geänderter Bezeichnungs­weise der Indizes): (31)

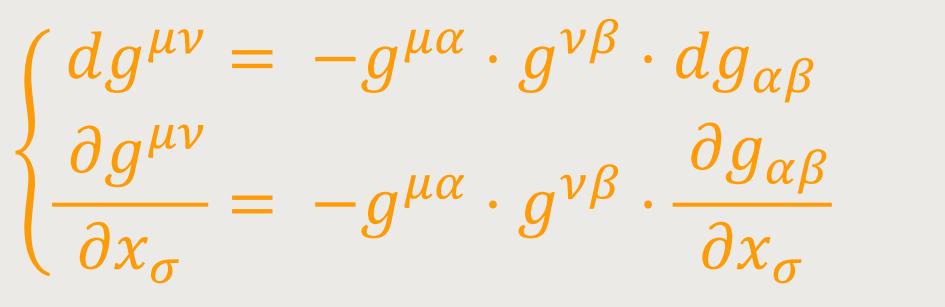
bzw.: (32)

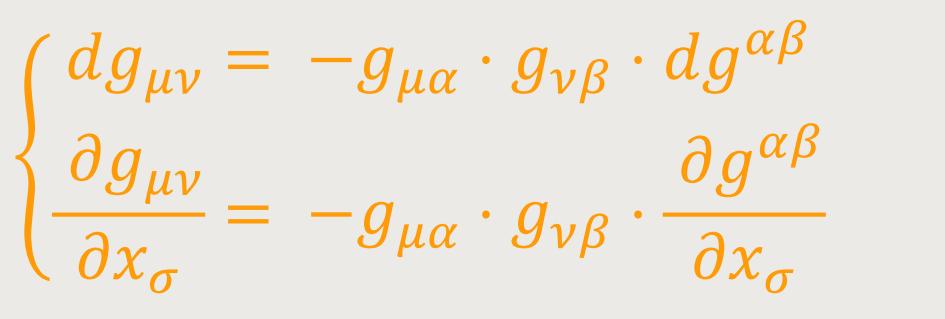
Die Beziehung (31) erlaubt eine Umformung, von der eben­falls des Öfteren Gebrauch gemacht wird. Gemäß (21) ist: (33)

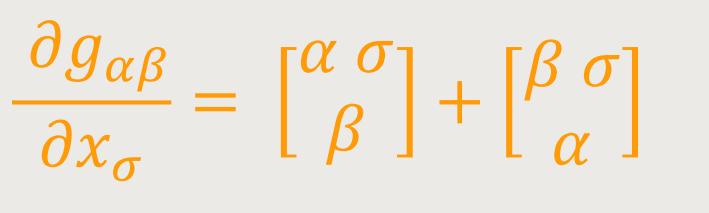
Setzt man dieen Ausdruck in die zweite der Formeln (31) ein, so erhält man mit Rück­sicht auf (23): (34)

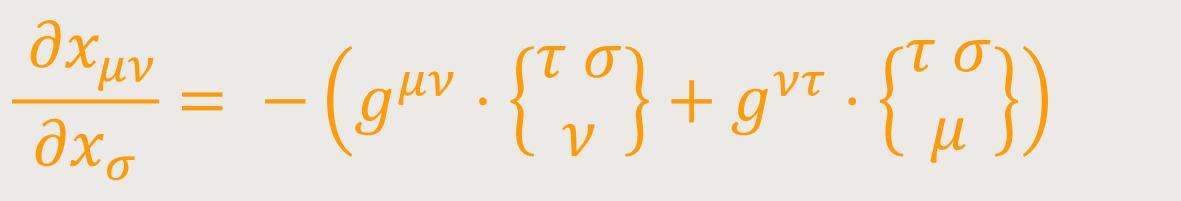
Durch Substitution der rechten Seite von (34) in (29) ergibt sich: (29a)

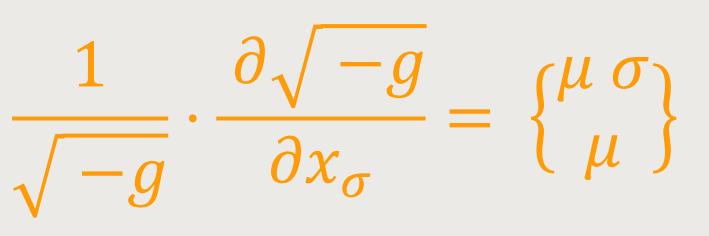
Divergenz des kontra­varianten Vierer­vektors. Multi­pliziert man (26) mit dem kontra­varianten Fundamental­tensor g^μν (innere Multi­plikation), so nimmt die rechte Seite nach Umformung des ersten Gliedes zunächst folgende Form an:

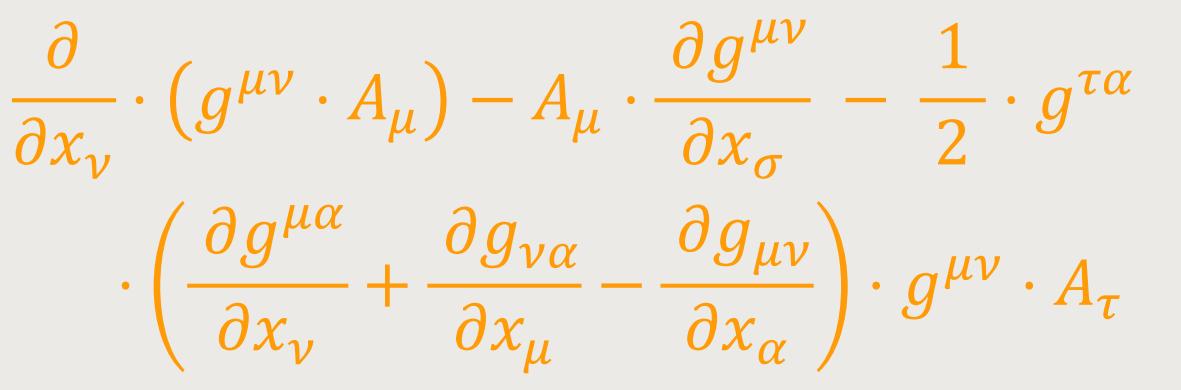
Das letzte Glied dieses Aus­drucks kann gemäß (31) und (29) in folgende Form gebracht werden:

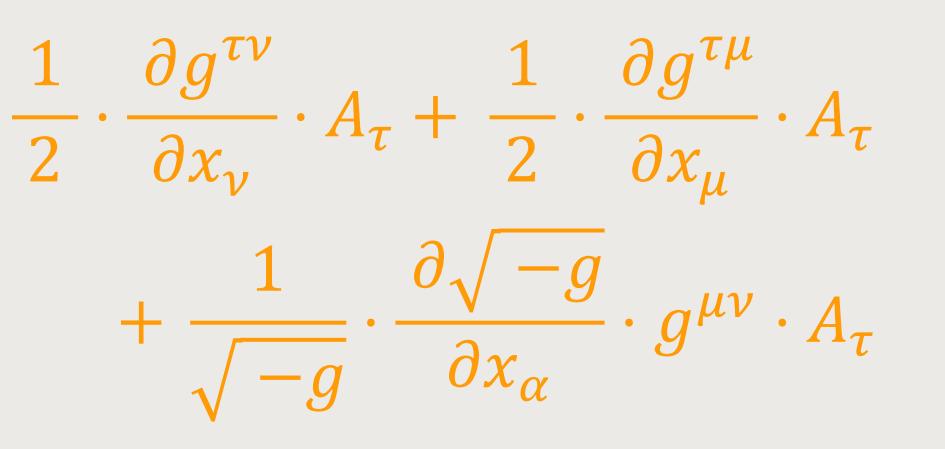
Da es auf die Benennung der Summations­indizes nicht ankommt, heben sich die beiden ersten Glieder dieses Aus­drucks gegen das zweite des obigen weg. Das letzte Glied lässt sich mit dem ersten des obigen Aus­drucks vereinigen. Setzt man noch

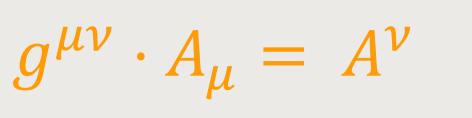
wobei A^ν ebenso wie A_μ ein frei wähl­barer Vektor ist, so erhält man abschließend: (35)

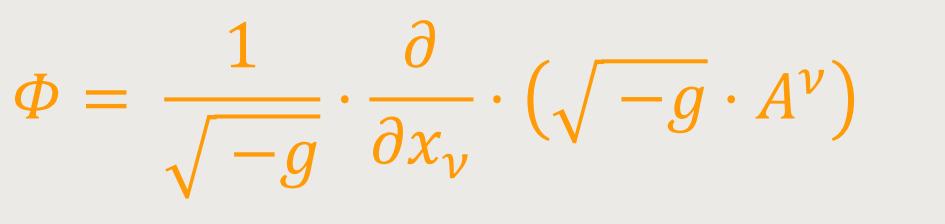
Dieser Skalar ist die Divergenz des kontra­varianten Vierer­vektors A^ν.

„Rotation” des (kovarianten) Vierer­vektors. Das zweite Glied in (26) ist in den Indizes μ und ν symmetrisch. Es ist deshalb A_μν − A_νμ ein besonders einfach gebauter (antisymmetrischer) Tensor. Man erhält: (36)

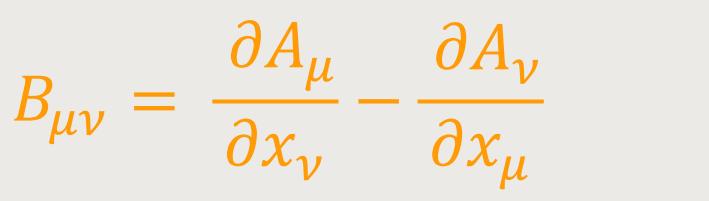
Antisymmetrische Erweiterung eines Sechser­tensors. Wendet man (27) auf einen anti­symmetrischen Tensor zweiten Ranges A_μν an, und bildet hierzu die beiden durch zyklische Ver­tauschung der Indizes μ, ν, σ entstehenden Gleichungen und addiert diese drei Gleichungen, so erhält man den Tensor dritten Ranges: (37)

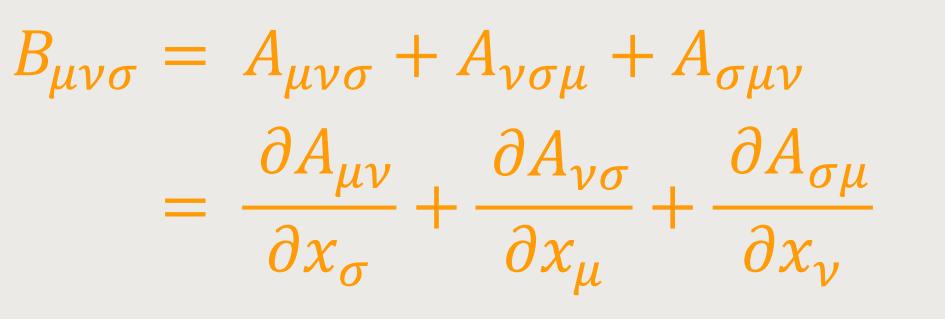
Nach Einsteins Worten sei leicht zu beweisen ist, dass dieser Tensor anti­symmetrisch ist.

Divergenz des Sechser­vektors. Multi­pliziert man (27) mit g^μα g^νβ (gemischte Multi­plikation), so erhält man eben­falls einen Tensor. Das erste Glied der rechten Seite von (27) kann man in folgender Form schreiben:

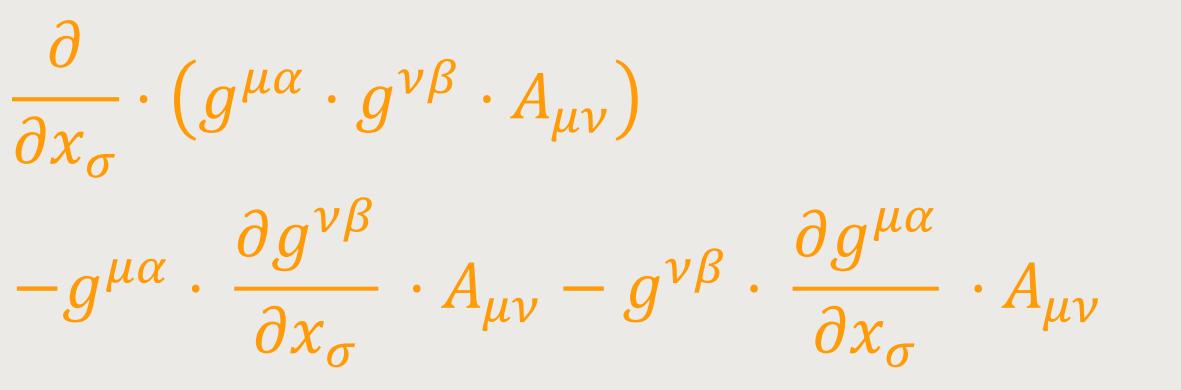
Ersetzt man g^μα g^νβ A_μνσ durch A_σ^αβ sowie g^μα g^νβ A_μν durch A^αβ, und ersetzt man in dem umge­formten ersten Teil

mithilfe (34), so entsteht aus der rechten Seite von (27) ein Ausdruck mit sieben Gliedern, von dem sich vier Glieder weg­heben. Letztlich bleibt übrig: (38)

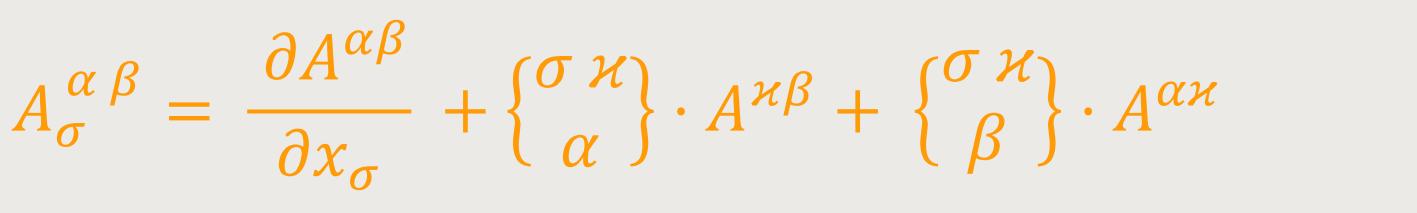
Dies ist der Ausdruck für die Erweiterung eines kontra­varianten Tensors zweiten Ranges, der sich ent­sprechend auch für kontra­variante Tensoren höheren und niedrigeren Ranges bilden lässt.

Es ist anzumerken, dass sich auf analogem Weg auch die Erweiterung eines gemischten Tensors A_μ^α bilden lässt: (39):

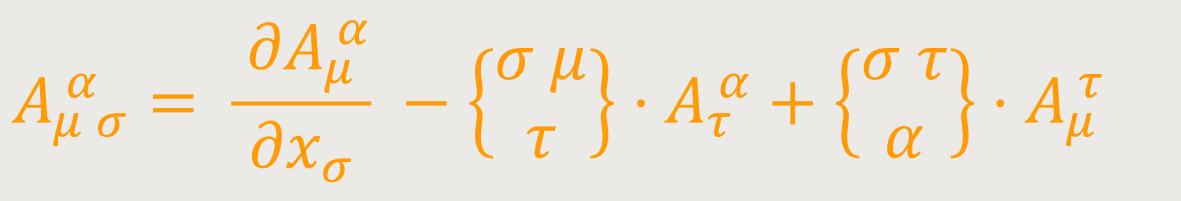
Durch Verjüngung von (38) bezüglich des Indizes β und σ (innere Multi­plikation mit δ_β^σ) erhält man den kontra­varianten Vierer­vektor:

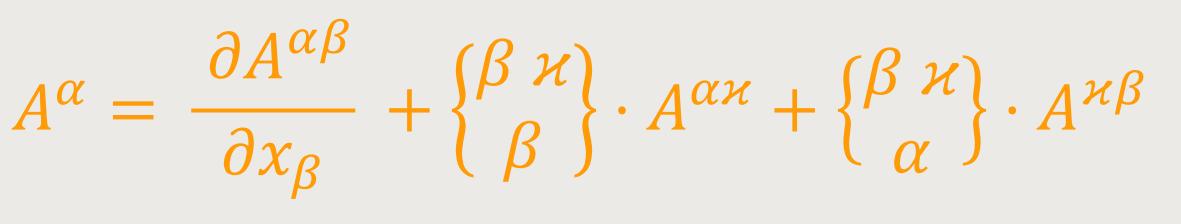
Wegen der Symmetrie von { ^β_α^ϰ } bezüglich der Indizes β und ϰ ver­schwindet das dritte Glied der rechten Seite, falls A^αβ ein anti­symmetrischer Tensor ist, was voraus­gesetzt wird. Das zweite Glied lässt sich gemäß (29a) umformen. Man erhält daher: (40)

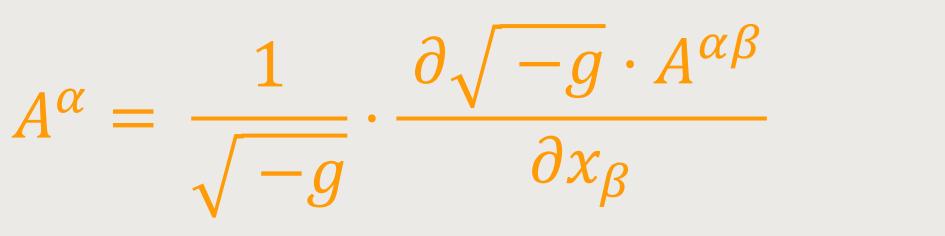
Dies ist der Ausdruck der Divergenz eines kontra­varianten Sechser­vektors.

Divergenz des gemischten Tensors zweiten Ranges. Bilden wir die Ver­jüngung von (39) bezüg­lich der Indizes α und σ, so erhalten wir mit Rücksicht auf (29a): (41)

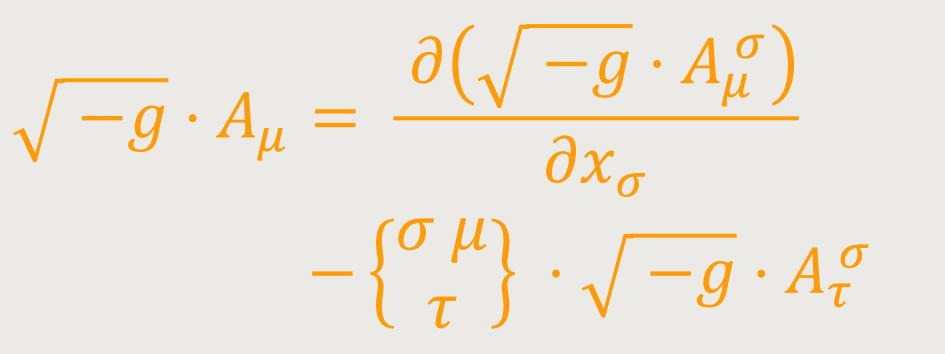
Führt man im letzten Glied den kontra­varianten Tensor A^ϱσ = g^ϱτ A_τ^σ ein, so nimmt es folgende Form an:

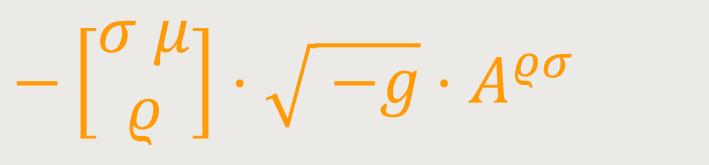
Ist ferner der Tensor A^ρσ ein symmetrischer, so reduziert sich der Ausdruck auf:

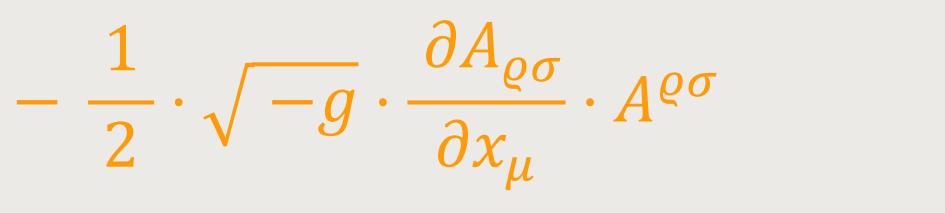
Hätte man statt A^ϱσ den eben­falls symmetrischen kovarianten Tensor A_ϱσ = g_ϱα g_σβ A^αβ eingeführt, so würde das letzte Glied auf Grundlage von (31) folgende Form annehmen:

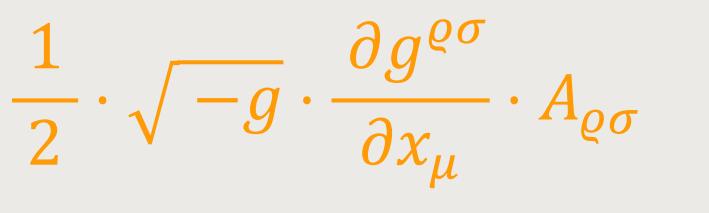
In dem betrachteten Symmetrie­fall kann also (41) auch durch die Formen: (41a)

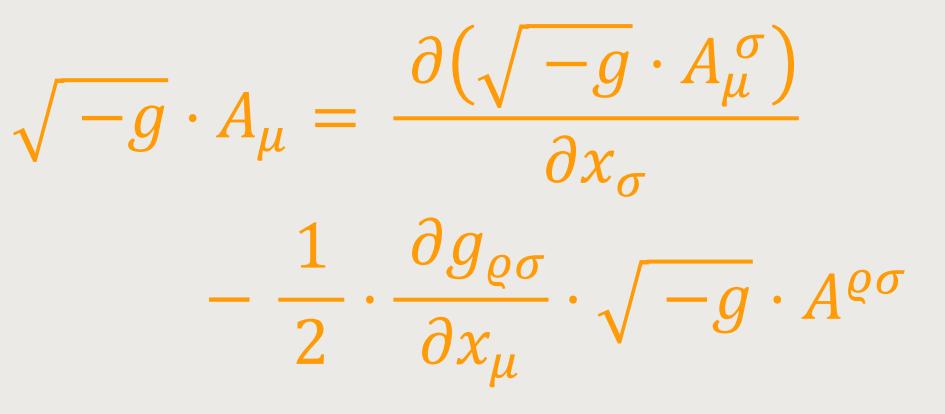
und: (41b)

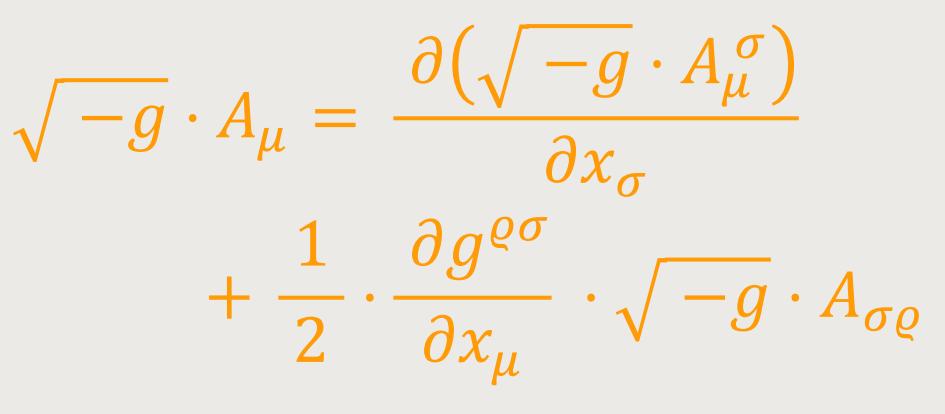
ersetzt werden, von dem im Nach­folgenden Gebrauch gemacht wird.

§ 12. Der Riemann-Christoffelsche Tensor.

Nun geht es um Frage nach denjenigen Tensoren, welche aus dem Fundamental­tensor der g_μν allein durch Differen­tiation gewonnen werden können. Die Antwort scheint nach Einstein zunächst auf der Hand zu liegen. Man setzt in (27) statt des beliebig gegebenen Tensors A_μν den Fundamental­tensor g_μν ein, und erhält dadurch einen neuen Tensor, nämlich die Erweiterung des Fundamental­tensors. Man kann sich jedoch leicht davon über­zeugen, dass diese letztere in gleicher Weise ver­schwindet, indem man auf folgendem Weg zum Ziel gelangt. Man setzt in (27) folgendes ein:

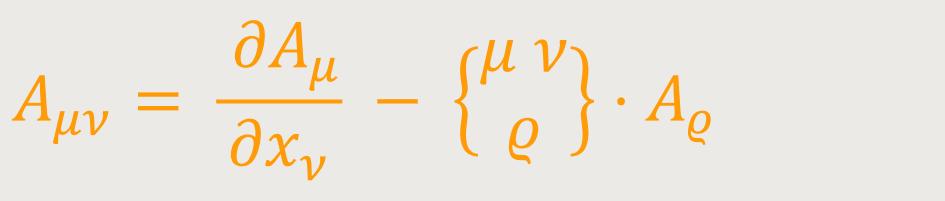
das heißt, die Erweiterung des Vierer­vektors A_ν. Dann erhält man (bei etwas geänderter Benennung der Indizes) den Tensor dritten Ranges:

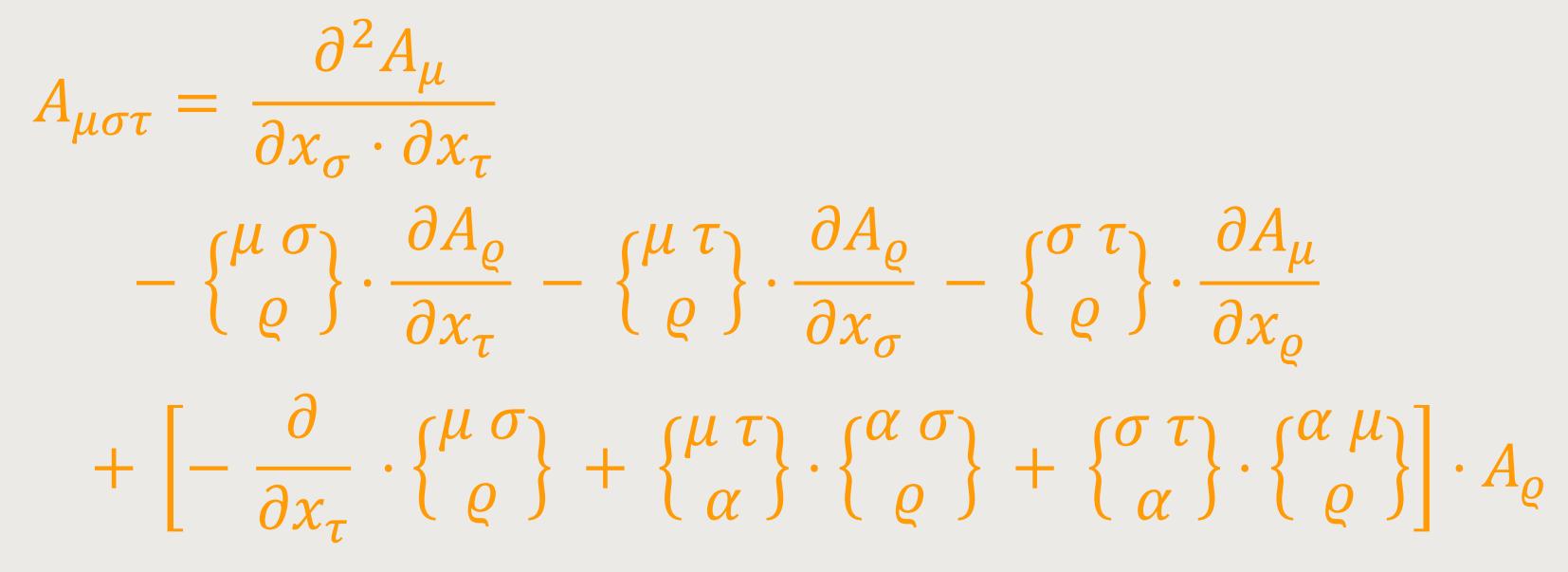
Dieser Ausdruck lädt nach Einsteins Worten förmlich zur Bildung des Tensors A_μστ − A_μτσ ein. Denn dabei heben sich folgende Terme des Ausdrucks für A_μστ gegen solche von A_μτσ weg: Das erste Glied, das vierte Glied, sowie das dem letzten Term in der eckigen Klammer entspre­chende Glied. Denn alle diese sind in σ und τ symmetrisch. Gleiches gilt von der Summe des zweiten und dritten Gliedes. Man erhält entspre­chend: (42)

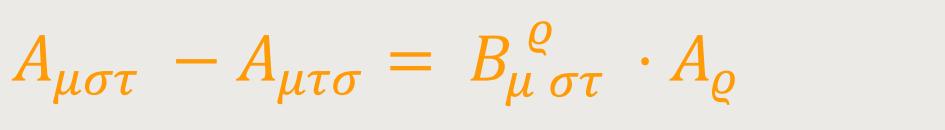
bzw.: (43)

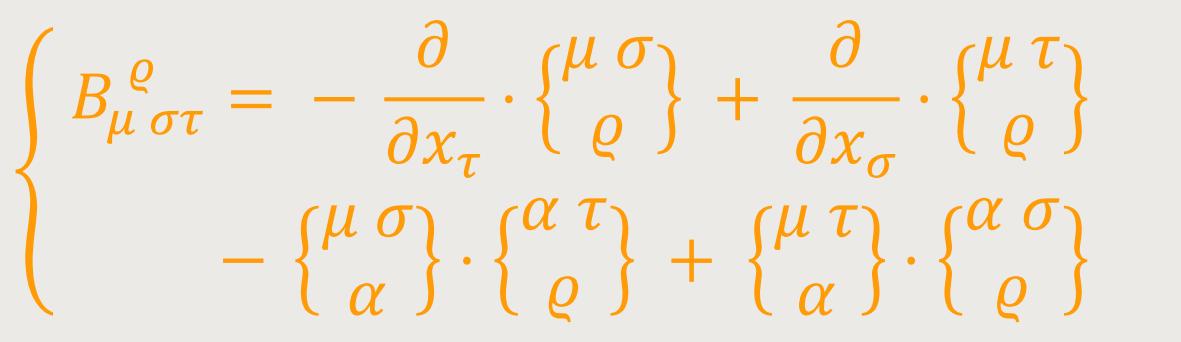
Wesentlich ist an diesem Resultat, dass auf der rechten Seite von (42) nur die A_ϱ, aber nicht mehr ihre Ableitungen auf­treten. Aus dem Tensor­charakter von A_μστ − A_μτσ in Verbin­dung damit, dass A_ϱ ein frei wähl­barer Vierer­vektor ist, folgt, auf Grund­lage der Resultate des §7, das B_μ^ρ_στ ein Tensor ist. In diesem Fall ein Riemann-Christoffel­scher Tensor.

Die mathematische Bedeutung dieses Tensors lässt sich wie folgt beschrieben. Wenn das Kontinuum so beschaffen ist, dass es ein Koordinaten­system gibt, bezüglich dessen g_μν Konstanten sind, so ver­schwinden alle R_μ^ϱ_στ. Wählt man statt des ursprüng­lichen Koordi­naten­systems ein beliebiges neues, so werden die auf letzteres bezogenen g_μν keine Konstanten sein.

Der Tensorcharakter von R_μ^ϱ_στ bringt es aber mit sich, dass diese Kompo­nenten auch in dem beliebig gewählten Bezugs­system gänz­lich ver­schwinden. Das Ver­schwinden des Riemannschen Tensors ist also eine not­wendige Bedingung dafür, dass durch geeignete Wahl des Bezugs­systems die Konstanz der g_μν herbei­geführt werden kann. In vor­liegender Frage­stellung ent­spricht dies dem Fall, dass bei passender Wahl des Koordinaten­systems in begrenzten raum­zeitlichen Gebieten die Spezielle Relativitätstheorie gilt.

Durch Verjüngung von (43) bezüg­lich des Indizes τ und ϱ erhält man den kovarianten Tensor zweiten Ranges: (44)

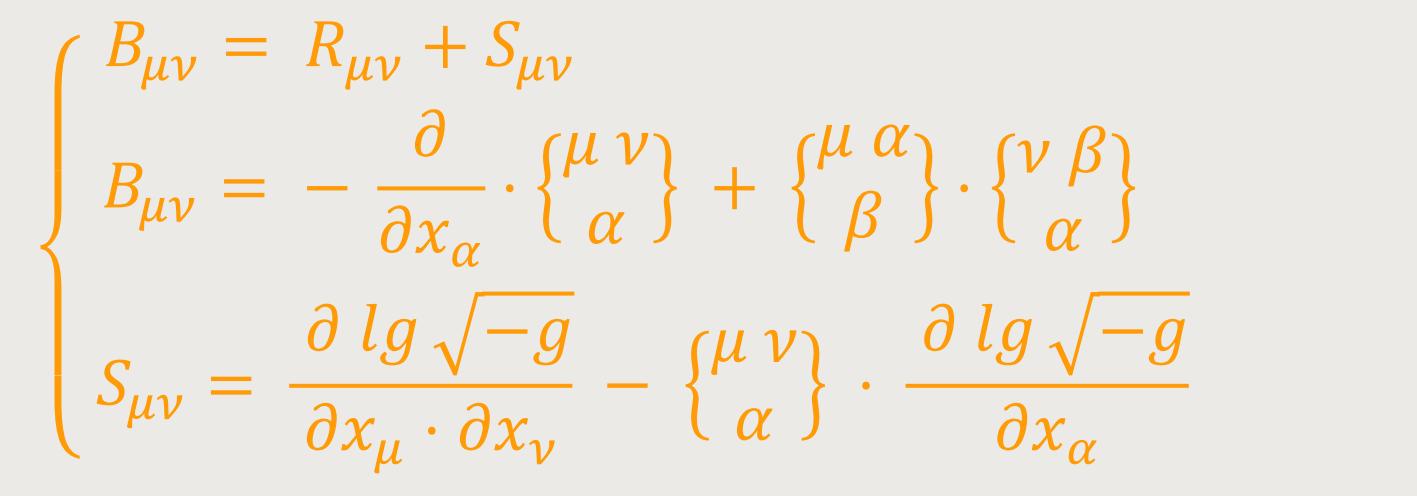
Bemerkung über die Koordinaten­wahl. Es ist schon in §8 im Anschluss an die Gleichung (18a) erwähnt worden, dass die Koordinaten­wahl bevorzugt so getroffen werden kann, dass √−g = 1 wird. Ein Blick auf die in den beiden letzten Para­graphen erlangten Gleichungen zeigt, dass durch eine solche Wahl die Bildungs­gesetze der Tensoren eine bedeutende Verein­fachung erfahren. Besonders gilt dies für den soeben ent­wickelten Tensor B_μν, welcher in der hier dar­gelegten Theorie eine fundamen­tale Rolle spielt. Die ins Auge gefasste Speziali­sierung der Koordi­naten­wahl bringt nämlich das Ver­schwinden von S_μν mit sich, so dass sich der Tensor B_μν auf R_μν reduziert.

Aus diesem Grund ging Einstein im Nach­folgenden dazu über, alle Beziehungen in der verein­fachten Form anzugeben, welche die genannte Speziali­sierung der Koordi­naten­wahl mit sich bringt. Nach seinen Worten sei es dann ein Leichtes, auf die all­gemein kovarianten Gleichungen zurück­zugreifen, falls dies in einem speziellen Fall erwünscht erscheint.

⇦ Kapitel Kapitel ⇨