Der „Minkowski-Raum” ist benannt nach Hermann Minkowski (1864-1909), der sich dem Studium der Mathe­matik und Physik gewidmet hat. Bei diesem Raum handelt es sich um einen 4-dimen­sionalen Raum, in welchem sich die Relativitäts­theorie elegant formu­lieren lässt. Um das Jahr 1907 erkannte Minkowski, dass die Arbeiten von Hendrik A. Lorentz (1904) und Albert Einstein (1905) zum Thema „Relativitäts­theorie” in einem nicht-euklidischen Raum verstanden werden können. Minkowski vermutete, dass Raum und Zeit in einem 4-dimen­sionalen Raum-Zeit-Kontinuum mit­einander verbunden sind.

Drei der Koordinaten des Minkowski-Raums sind die klassischen des Eukli­dischen Raums. Hinzu kommt eine vierte Koordinate für die Zeit. Der Minkowski-Raum ist also analog wie ein 4-dimen­sionaler eukli­discher Raum aufgebaut. Doch wegen der unter­schied­lichen Struktur von Raum- und Zeit­koordinaten unter­scheiden sich beide Räume voneinander.

Der Minkowski-Raum kann als 4-dimen­sionaler reeller Vektor­raum aufgefasst werden, in welchem das Skalar­produkt nicht durch den üblichen Ausdruck, sondern durch eine sogenannte nicht­ausgeartete „Bilinear­form” vom Index 1 gegeben ist.

Als Bilinear­form bezeichnet man in der linearen Algebra eine Funktion, die zwei unabhän­gigen Vektoren einen Skalar­wert zuordnet und die linear in ihren beiden Argumenten ist. Insofern ist diese Bilinear­form nicht positiv definiert. Hierbei ordnet man den Minkowski-Vektoren (vier an der Zahl), man spricht auch von Ereig­nissen, 4-kompo­nentige Elemente x bzw. y zu. Folgende Regel ist gebräuchlich:

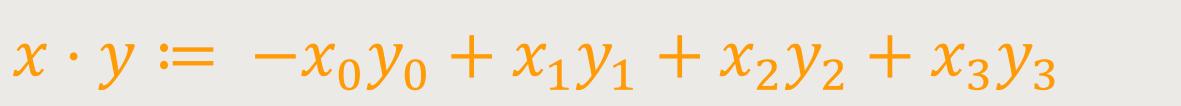
Die Koordinate x₀ = c · t geht mittels der Licht­geschwin­dig­keit c aus der Zeit­komponente t hervor.

In der Allgemeinen Relativitäts­theorie wird all­gemein obige Signatur (−,+,+,+) verwendet. Eine physikalisch äquivalente umgekehrte Signatur (+,−,−,−) ist in der Teil­chen­physik weit verbreitet. Die Zeit wird manch­mal auch als vierte (x₄ y₄) statt als nullte Koordinate geführt.

Alternativ kann man das innere Produkt zweier Elemente des Minkowski-Raums auch als Wirkung des metrischen Tensors η_μν auffassen:

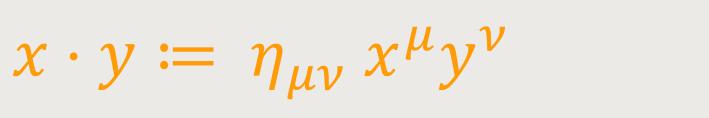
In der oben dargestellten Tensor-Schreib­weise unter­scheidet man zwischen kontra­varianten (Indizes oben) und kovarianten (Indizes unten) Vektor­komponenten.

Ein 4-dimen­sionaler Raum mit Minkowski-Metrik wird definiert als:

(Der Abstand zweier Vierer-Vektoren r₁ und r₂ im Minkowski-Raum ist damit gegeben durch:

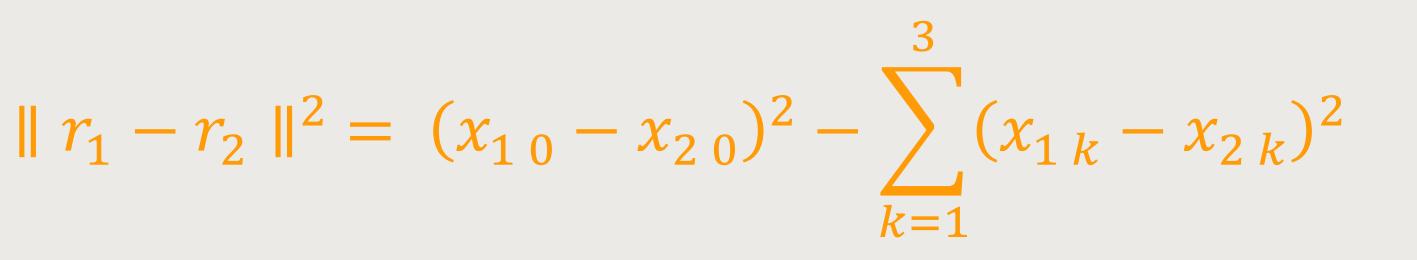
Die inhomogene Lorentz­gruppe lässt den Vierer-Abstand invariant; sie umfasst die räum­lichen und zeit­lichen Trans­lationen und Spiege­lungen sowie die Trans­formationen der homogenen Lorentz­gruppe.

Aufgrund der Lorentz-Trans­formation lässt sich erkennen, dass die Zeit­koordinate mit einbe­zogen werden muss, weil sich die Zeit beim Trans­formieren auch ändert. Deswegen muss die Zeit in den grafischen Darstel­lungen mit berück­sichtigt werden. Und dem­entspre­chend bewegt man sich in einem 4-dimen­sionalen Raum.

Minkowski hatte basierend auf den Arbeiten von Lorentz und Einstein die Idee, Raum und Zeit nicht mehr als zwei separate physika­lische Einheiten zu sehen, sondern beide in einem Modell zu vereinigen.

Minkowski unter­teilte seine Argumen­tation in 5 Abschnitte, in welchen er schritt­weise ausführte, wie man von der gegen­wärtig ange­nommenen Mechanik allein durch rein mathe­matische Über­legungen zu verän­derten Ideen über Raum und Zeit kommen könnte. Zunächst bezog sich Minkowski auf die Gleichungen der Newton'schen Mechanik und deren zwei­facher Invarianz (Unver­änder­lich­keit). Zum einen bleibt deren Forma­lismus erhalten, selbst wenn man das zugrunde gelegte räum­liche Koordinaten­system einer beliebigen Lage­verän­derung unter­zieht. Selbst wenn man seinen Bewegungs­zustand verändert, indem man ihm irgend­eine gleich­förmige Trans­lation aufprägt. Und selbst der Null­punkt der Zeit spielt hierbei keine Rolle.

Nach Minkowskis Worten ist man gewohnt, die Axiome der Geometrie als unver­änder­lich anzusehen, wenn man bereit ist, sich mit den Grund­sätzen der Mechanik zu beschäf­tigen. Aus diesem Grund, so bemerkte Minkowski, würde man auch die Unver­änder­lich­keit selten in einem Atemzug erwähnen.

Die Unver­änder­lich­keit beider Bereiche beinhaltet eine gewisse Gruppe von Trans­formationen für die Differen­tial­gleichungen der Mechanik. Die Trans­formationen in der Geometrie sieht man als einen fundamen­talen Charakter des Raums an. Die Trans­formationen der Mechanik will man aber ungern darauf anwenden, weil es schwer zu ermessen ist, ob sich ein Raum, den man als ruhend betrachtet, sich nicht doch in einer gleich­förmigen Trans­lation (Bewegung) befindet. Dieser gänz­lich eigen­ständige Charakter hat nach Minkowskis Ansicht viele seiner­zeit davon abge­halten, beide Bereiche harmonisch mit­einander zu verbinden.

Um das graphisch zu veran­schau­lichen, wählte er, wie wir es auch heute noch gewohnt sind, x, y, z als recht­winklige Koordi­naten für einen gedachten Raum. Für die Zeit wird t gewählt. Gemäß unserer Wahr­nehmung sind Ort und Zeit stets mit­einander ver­bunden. Niemand betrachtet einen Ort los­gelöst von der Zeit oder anders herum, wenn­gleich beide Begriffe eine unter­schied­liche Bedeutung haben.

In unserem Beispiel soll ein Raum­punkt, der einem Werte­system, bestehend aus x, y, z, t ent­spricht, im weiteren Verlauf „Weltpunkt” genannt werden. Die Gesamt­heit aller denkbaren Werte­systeme x, y, z, t soll dementspre­chend „Welt” heißen. Bereits an dieser Stelle betonte Minkowski, dass, würde man vier Welt­achsen mit Kreide auf eine Tafel zeichnen, bereits eine dieser Achsen aus lauter schwin­genden Molekülen bestünde, die ihrer­seits mit der Erd­rotation eine Kurve im All beschreiben würde.

Der Raum unserer Anschauung soll zudem kein Vakuum aufweisen, sodass an allen Orten und zu jeder Zeit etwas wahr­genommen werden kann. Minkowski wählte dafür nicht den Begriff „Materie” oder „Elektrizität”, sondern wählte bewusst den Begriff „Substanz”. Dabei konzen­trieren wir uns auf den im Welt­punkt x, y, z, t vorhan­denen substan­ziellen Punkt, wobei wir in der Lage sind, diesen substan­ziellen Punkt zu jedem Zeit­punkt zu lokalisieren.

Einem Zeitpunkt dt sollen die Ände­rungen dx, dy, dz der Raum­koordi­naten dieses substan­ziellen Punktes ent­sprechen. Als Abbild beschreibt dieser substan­zielle Punkt einen Kurven­verlauf bzw. eine Welt­linie, deren Punkte sich ein­deutig auf den Parameter t von −∞ bis +∞ beziehen lassen. Die ganze gedachte „Welt” lässt sich in der­artige Welt­linien auf­lösen, wobei zwischen den einzelnen Welt­linien die Gesetze der Physik und deren Wechsel­wirkungen zu beobachten sind.

Durch die Begriffe „Raum” und „Zeit” fallen die x, y, z-Mög­lich­keiten bezogen auf t = 0 und ihre zwei Gegen­sätze t > 0 und t < 0 auseinander. Bestimmt man den Null­punkt von Raum und Zeit, so bedeutet das für die Trans­forma­tionen der Mechanik, dass die x, y, z-Achsen zum Zeit­punkt t = 0 beliebig um den Null­punkt gedreht werden dürfen. Das ent­spricht auch den homogenen linearen Trans­formationen des Ausdrucks:

Eine weitere Trans­formation bedeutet, dass wir, eben­falls ohne den Ausdruck der mecha­nischen Gesetze zu verändern, x, y, z, t durch

mit beliebigen Konstanten α, β, γ ersetzen dürfen. Der Zeit­achse kann hier­nach eine völlig beliebige Richtung entspre­chend der Vorgabe t > 0 in der grafisch dar­gestellten oben angeord­neten „halben Welt” gegeben werden.

Welche Verbindung besteht nun zwischen der Forderung der Ortho­gonalität im Raum und der völligen Freiheit der Zeit­achse nach oben hin?

Um dies zu verdeut­lichen, wird ein weiterer Parameter c hinzu­gefügt, wodurch sich folgende Beziehung ergibt:

Daraus ergeben sich zwei durch den Punkt t = 0 getrennte Schalen, in Anlehnung eines zweischaligen Hyper­boloids. Zunächst betrach­ten wir die in positive Richtung zeigende Schale im Bereich t > 0. Außer­dem werden jetzt die homogenen linearen Trans­forma­tionen von x, y, z, t in vier neue Variable mit der Bezeich­nung x', y', z', t' über­tragen, wobei der Ausdruck dieser Schale in den neuen Variablen entspre­chend wird. Zu diesen Trans­forma­tionen gehören offenbar die Drehungen des Raums um den Null­punkt. Ein volles Verständnis der übrigen Trans­forma­tion ergibt sich bereits, wenn wir uns auf eine Trans­forma­tion beschrän­ken, bei der y und z unver­ändert bleiben. Hierzu betrachten wir in nach­folgender Grafik (Abb. 1) einen Schnitt durch jene Schale, deren Schnitt­ebene die x-t-Achse betrifft.

Abb. 1: Zeigt den von Minkowski skizzierten Hyperbelast mit seinen Asymptoten

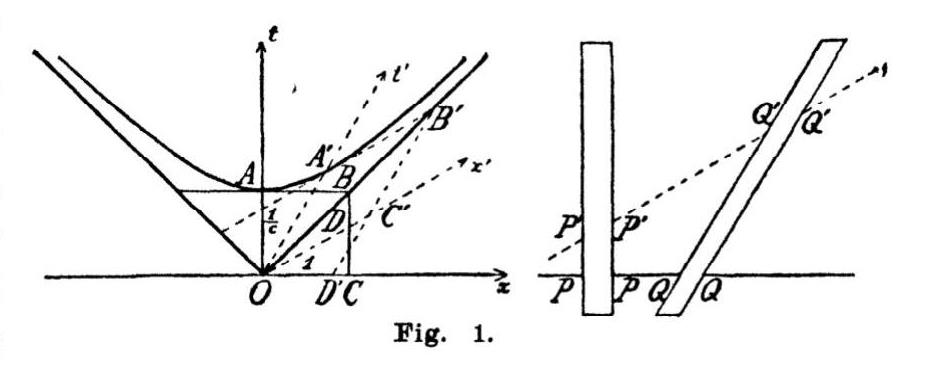
Es geht im Wesent­lichen um den oberen Hyperbelast mit seinen Asymptoten, der wie folgt definiert ist:

Zusätz­lich wird ein beliebiger Radius­vektor OA', ausgehend vom Null­punkt O, ein­getragen. Außer­dem wird eine Tangente im Punkt A' an die Hyperbel bis zum Schnitt­punkt B' mit der Asymptote rechts davon gelegt. Die Eck­punkte OA' B' werden nun noch zu einem Parallelo­gramm mit den Eck­punkten OA' B' C' vervoll­ständigt. Abschlie­ßend wird das für die Punkte B' C' bis zum Schnitt D' mit der x-Achse durchgeführt.

Betrachtet man nun die Punkte OC' und OA' als Achsen für die Parallel­koordinaten x', t' mit den Maßstäben OC' = 1 und OA' = 1/c, so erhält man für jenen Hyperbelast wieder den Ausdruck c² t'² - x'² = 1, t' > 0. Und der Über­gang von x, y, z, t zu x', y', z', t' ist eine der gesuchten Trans­formationen.

Zu den vorge­nannten Trans­forma­tionen sollen nun noch beliebige Verschie­bungen des Raum-Zeit-Null­punktes hinzu­gefügt werden. Dadurch erhalten wir graphisch eine von dem Parameter c abhängige Gruppe von Trans­forma­tionen, die Minkowski mit G_c bezeichnete.

Lassen wir jetzt c ins Unend­liche wachsen, also 1/c nach Null konver­gieren, so fällt in der obigen Abbildung auf, dass sich der Ast der Hyperbel immer mehr der x-Achse annähert. Der Asymptoten­winkel breitet sich somit zu einem gestreckten Winkel aus. Daraus ergibt sich eine Trans­forma­tion, an deren Grenze die t'-Achse oberhalb eine beliebige Richtung haben kann, und x' sich immer mehr an x annähert. Unter Berück­sichti­gung, dass aus der Gruppe G_c am Grenz­punkt c = ∞, quasi der Gruppe G_∞, eine Gruppe wird, die den Gesetzen der Newton'schen Mechanik folgt. Bei dieser Tatsache, und dass G_c aus mathe­matischer Sicht einfacher zu beschreiben ist als G_∞, könnte man auf die Idee kommen, dass die Natur­erschei­nungen weniger mit der Gruppe G_∞, als vielmehr mit der Gruppe G_c beschrieben werden können, bei der der Parameter c äußerst groß gewählt wird. Das wäre aus Sicht Minkowskis ein Triumph der reinen Mathematik gewesen.

Um Missverständ­nisse auszuräumen, legte Minkowski fest, um welchen Wert es sich bei dem Para­meter c handelt. Für c soll die Licht­geschwin­dig­keit im Vakuum voraus­gesetzt werden, in welchem ledig­lich die elektro­magne­tischen Wechsel­wirkungen zum Tragen kommen. Die Unveränder­lich­keit der Natur­gesetze soll daher für die Gruppe G_c gelten.

Auf Grund­lage aller Natur­erschei­nungen kann durch konse­quente Annähe­rung ein Bezugs­system x, y, z, t als Raum-Zeit-Kontinuum abgeleitet werden, welches den Gesetzen der Natur folgt. Hierbei ist das Bezugs­system jedoch nicht durch die Erschei­nungen ein­deutig fest­gelegt. Dement­spre­chend hielt Minkowski folgendes fest:
Das Bezugs­system lässt sich je nach Trans­forma­tion der Gruppe G_c beliebig verändern, ohne Einfluss auf die Natur­gesetze zu nehmen.

Zum Beispiel könnte man in obiger Abbildung t' der Zeit gleich­setzen. Aller­dings ist es dann aber notwendig, den Raum in seiner Gesamt­heit bezüg­lich der drei Parameter x', y, z zu definieren. Wobei die physikalischen Gesetze in einem Bezugs­system x', y, z, t' genauso gelten wie in einem Bezugs­system x, y, z, t. Das bedeutet, dass wir nicht mehr nur „den” Raum, im Sinne von nur einem, sondern „unendlich viele” Räume betrachten, genauso wie es im 3-dimen­sionalen Raum unend­lich viele Ebenen gibt.

Minkowski schloss den ersten Teil mit den Worten ab, dass auf diese Weise die 3-dimen­sionale Geometrie ein Kapitel der 4-dimen­sionalen Physik wird.

⇦ Kapitel Kapitel ⇨