§ 13. Bewegungsgleichung des materiellen Punktes im Gravitationsfeld.
Ausdruck für die Feldkomponenten der Gravitation.

Ein frei beweglicher, äußeren Kräften nicht unter­worfener Körper, bewegt sich nach der Speziellen Relativi­täts­theorie gerad­linig und gleich­förmig. Dies gilt auch nach der Allgemeinen Relativi­täts­theorie für einen Teil des 4-dimen­sionalen Raumes, in welchem das Koordi­naten­system K₀ so wähl­bar und so gewählt ist, dass die g_μν die in (4) gegebenen speziellen konstanten Werte haben.

Betrachtet man eben diese Bewegung von einem beliebig gewählten Koordi­naten­system K₁ aus, so bewegt er sich von K₁ aus, beurteilt nach den Über­legungen des §2 (Teil-A) in einem Gravi­tations­feld. Das Bewegungs­gesetz mit Bezug auf K₁ ergibt sich leicht aus folgender Über­legung. Mit Bezug auf K₀ ist das Bewegungs­gesetz eine 4-dimen­sionale Gerade, also eine geodätische Linie. Da nun die geodätische Linie abhängig vom Bezugs­system definiert ist, wird ihre Gleichung auch die Bewegungs­gleichung des materiellen Punktes in Bezug auf K₁ sein. Legt man fest: (45)

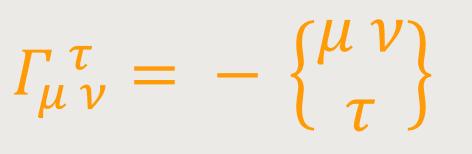
so lautet also die Gleichung der Punktbewegung in Bezug auf K₁: (46)

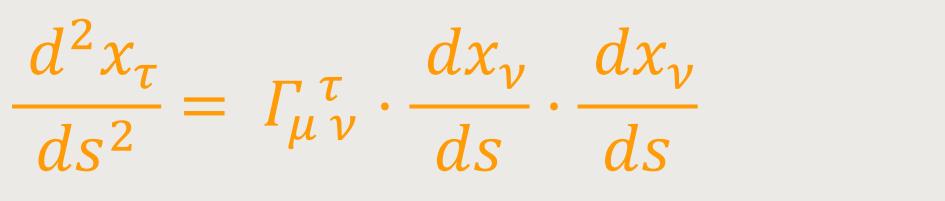
Es liegt nahe anzunehmen, dass dieses allgemein kovariante Gleichungs­system die Bewegung des Punktes im Gravi­tations­feld auch in dem Fall bestimmt, dass kein Bezugs­system K₀ existiert, bezüg­lich dessen in endlichen Räumen die Spezielle Relativi­täts­theorie gilt. Diese Annahme ist umso berechtigter, als (46) nur erste Ablei­tungen der g_μν ent­hält, zwischen denen auch im Spezial­fall der Existenz von K₀ keine Bezie­hungen bestehen.

Einstein ergänzt hierzu, dass erst zwischen den zweiten (und ersten) Ablei­tungen gemäß § 12 die Bezie­hungen B_μ^ϱ_στ = 0 bestehen.

Verschwinden die Γ_μ^τ_ν, so bewegt sich der Punkt gerad­linig und gleich­förmig. Diese Größen rufen also die Abwei­chung der Bewegung von der Gleich­förmig­keit hervor. Sie sind die Kompo­nenten des Gravi­tations­feldes.

§ 14. Die Feldgleichungen der Gravitation bei Abwesenheit von Materie.

Man unterscheidet im Folgenden zwischen „Gravi­tations­feld” und „Materie”, in dem Sinne, dass alles außer dem Gravi­tations­feld als „Materie” bezeichnet wird, also nicht nur die „Materie” im üblichen Sinne, sondern auch das elektro­magne­tisches Feld.

Als Nächstes gilt es, die Feldg­leichungen der Gravi­tation bei Abwesen­heit von Materie zu unter­suchen. Dabei ver­wendet man wieder dieselbe Methode wie im vorigen Para­graphen bei der Auf­stellung der Bewegungs­gleichung des materiellen Punktes. Ein Spezial­fall, in welchem die gesuchten Feld­gleichungen jeden­falls erfüllt sein müssen, ist der der ursprüng­lichen Relativitäts­theorie, in dem die g_μν gewisse konstante Werte haben. Dies sei der Fall in einem gewissen end­lichen Gebiet in Bezug auf ein bestimmtes Koordi­naten­system K₀. In Bezug auf dieses System ver­schwinden sämt­liche Kompo­nenten B_μ^ϱ_στ des Riemannschen Tensors [Gleichung (34)]. Diese ver­schwinden dann für das betrach­tete Gebiet auch bezüg­lich jedes anderen Koordi­naten­systems.

Die gesuchten Gleichungen des materie­freien Gravi­tations­feldes müssen also jeden­falls erfüllt sein, wenn alle B_μ^ϱ_στ ver­schwinden. Allerdings ist diese Bedingung sehr weit­reichend. Denn es ist nach­vollziehbar, dass z.B. das von einem Massen­punkt in seiner Umgebung erzeugte Gravi­tations­feld ziemlich sicher durch keine Wahl des Koordi­naten­systems „wegtransformiert”, das heißt auf den Fall konstanter g_μν trans­formiert werden kann.

Deshalb liegt es nahe, für das materie­freie Gravi­tations­feld das Ver­schwinden des aus dem Tensor B_μ^ϱ_στ abgeleiteten symmetrischen Tensors B_μν zu ver­langen. Man erhält so 10 Gleichungen für die 10 Größen g_μν, welche im Speziellen erfüllt sind, wenn sämtliche B_μ^ϱ_στ ver­schwinden. Diese Gleichungen lauten mit Rück­sicht auf (44) bei der von uns getroffenen Wahl für das Koordi­naten­system für das materie­freie Feld: (47)

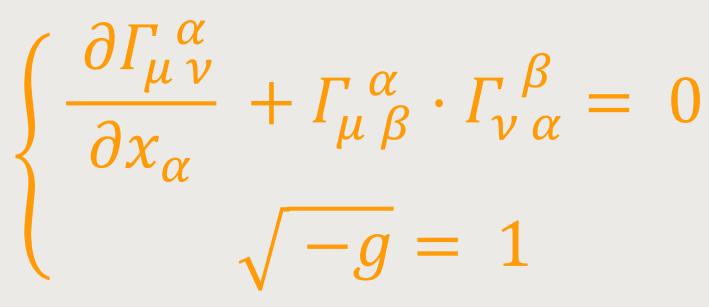
Nach Einsteins Worten muss darauf hingewiesen werden, dass der Wahl dieser Gleichungen ein Minimum von Willkür anhaftet. Denn es gibt außer B_μν keinen Tensor zweiten Ranges, der aus den g_μν und deren Ablei­tungen gebildet ist, keine höheren als zweite Ablei­tungen ent­hält, und in letzteren linear ist.

Einstein ergänzt hierzu, dass sich dies eigent­lich nur von dem Tensor B_μν + λg_μν (g^αβ B_αβ) behaupten lässt, wobei λ ein Konstante ist. Setzt man jedoch diesen = 0, so kommt man wieder zu den Glei­chungen B_μν = 0.

Dass diese Gleichungen sich aus der Forderung der allge­meinen Relativi­tät auf rein mathe­matischem Weg in Verbin­dung mit den Bewegungs­gleichungen (46) ergeben, und zwar in erster Nähe­rung das Newtonsche Attrak­tions­gesetz, sowie in zweiter Nähe­rung die Erklä­rung der von Le Verrier ent­deckten Perihel­bewegung des Merkur liefern, über­zeugten Einstein von der physika­lischen Richtig­keit der Theorie.

§ 15. Hamiltonsche Funktion für das Gravitationsfeld, Impulsenergiesatz.

Um zu zeigen, dass die Feld­gleichungen dem Impuls­energie­satz entsprechen, ist es am bequemsten, sie in folgender Hamiltonscher Form zu schreiben: (47a)

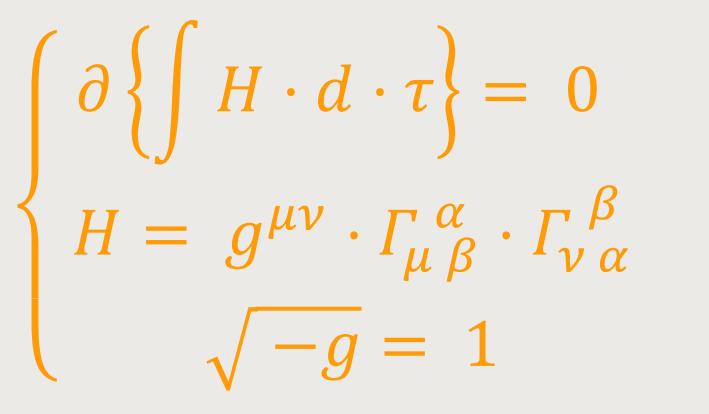
Dabei verschwinden die Varia­tionen an den Grenzen des betrach­teten begrenzten 4-dimen­sionalen Integrations­raumes.

Einstein zeigte zunächst, dass die Form (47a) mit den Gleichungen (47) äquivalent ist. Zu diesem Zweck betrachtet man H als Funktion der g^μν und der

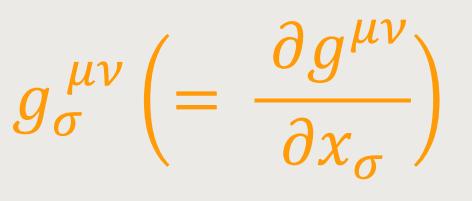
Dann ist zunächst

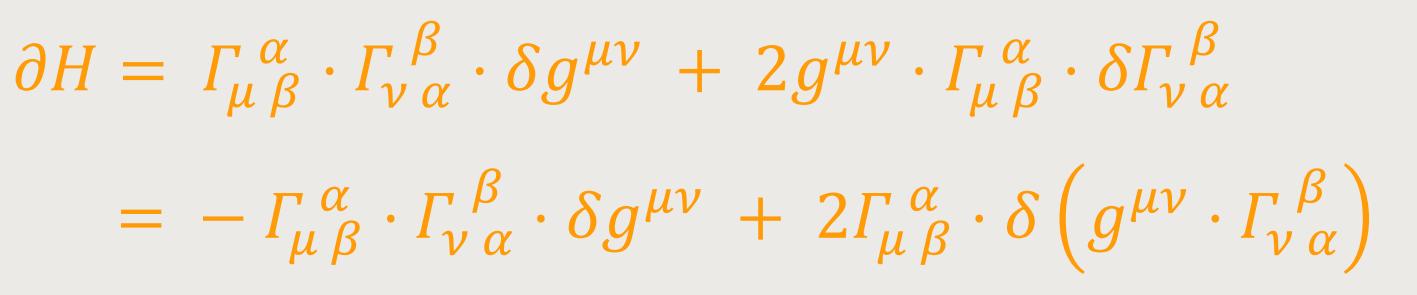
Nun ist aber

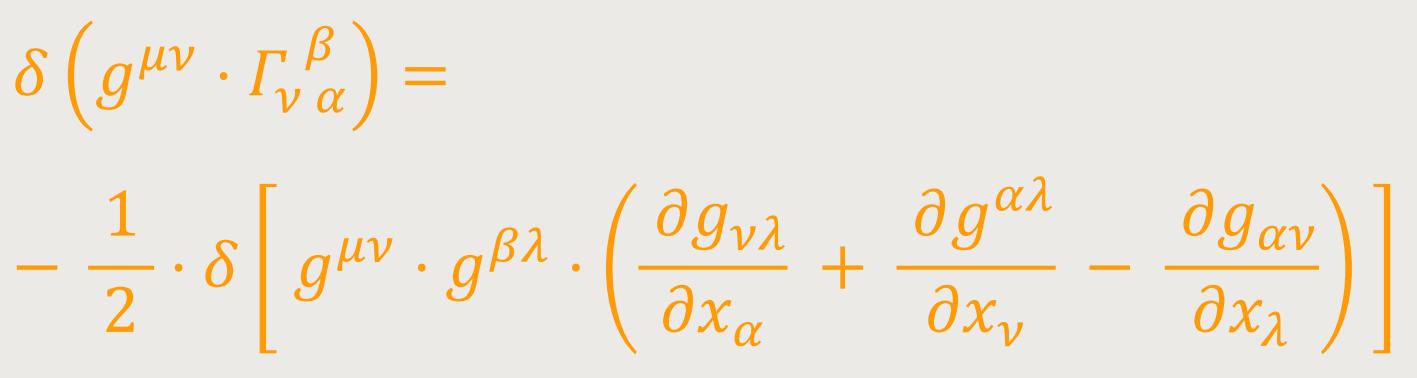
Die aus den beiden letzten Termen der runden Klammer hervor­gehenden Terme sind von verschie­denem Vor­zeichen und gehen aus­einander (da die Benennung der Summations­indizes belang­los ist) durch Ver­tauschung der Indizes μ und β hervor. Sie heben einander im Ausdruck für δH weg, weil sie mit der bezüg­lich der Indizes μ und β symmetrischen Größe Γ_μ^α_β multi­pliziert werden. Es muss also nur das erste Glied der runden Klammer berück­sichtigt werden, so dass man mit Rück­sicht auf (31) erhält:

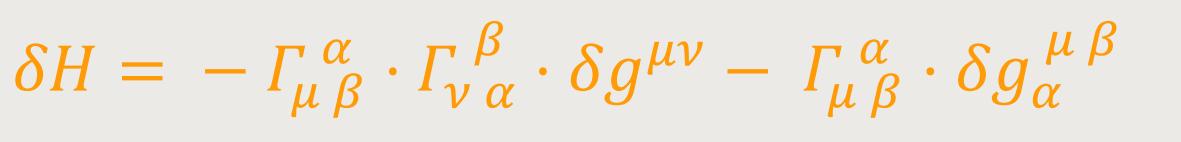
Daraus folgt demnach: (48)

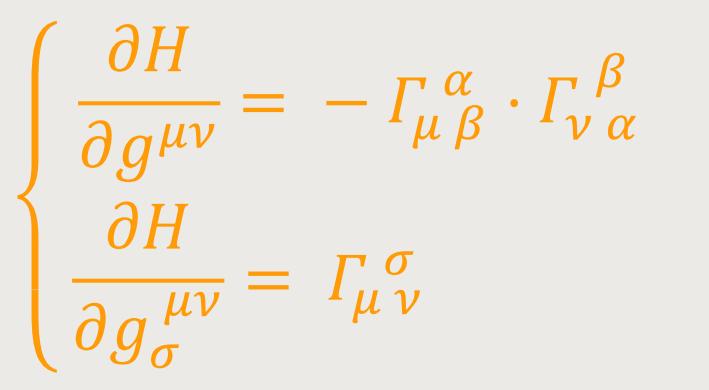
Die Ausführung der Variation in (47a) ergibt zunächst folgendes Gleichungs­system: (47b)

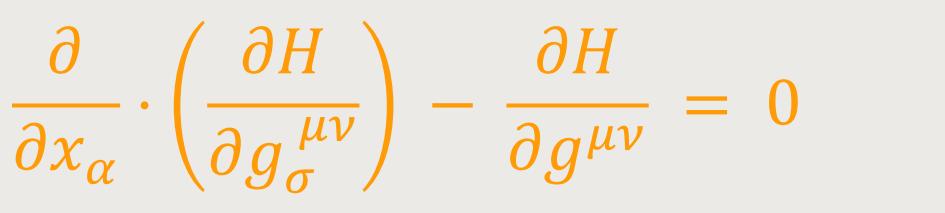
welches wegen (48) mit (47) über­einstimmt, was nach Einsteins Worten zu beweisen war. Multi­pliziert man (47b) mit g_σ^μν, so erhält man, weil

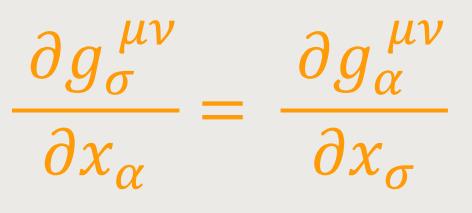
und folglich

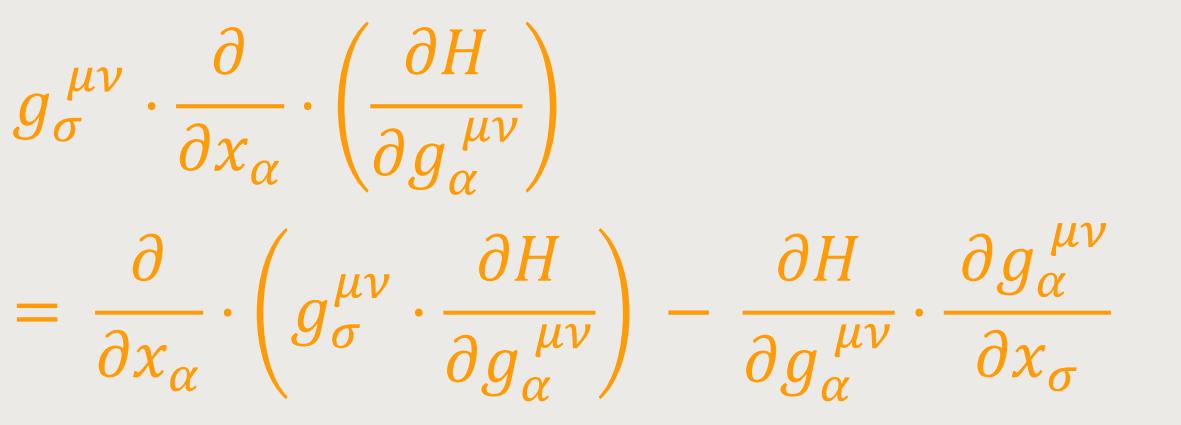
folgende Gleichung:

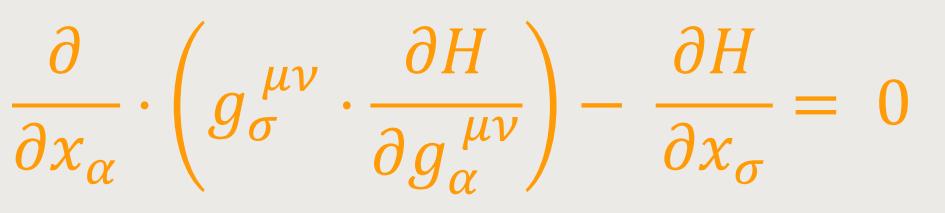
Oder: (49)

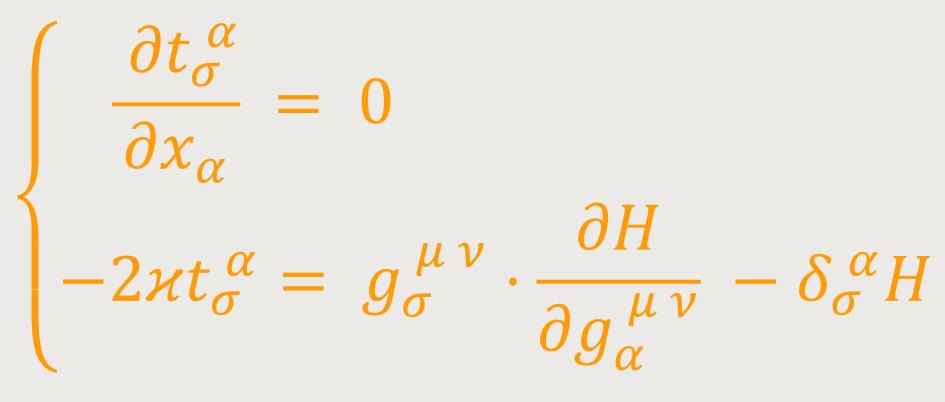
bzw. wegen (48), der zweiten Gleichung (47) und (34): (50)

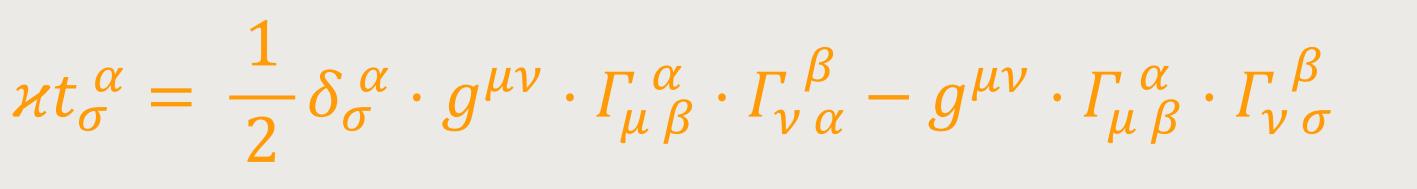
Es ist zu beachten, dass t_σ^α kein Tensor ist. Dagegen gilt (49) für alle Koordinaten­systeme, für welche √−g = 1 ist. Diese Gleichung drückt den Erhaltungs­satz des Impulses und der Energie für das Gravi­tations­feld aus. Tatsäch­lich liefert die Integration dieser Gleichung über ein 3-dimen­sionales Volumen V die vier Gleichungen: (49a)

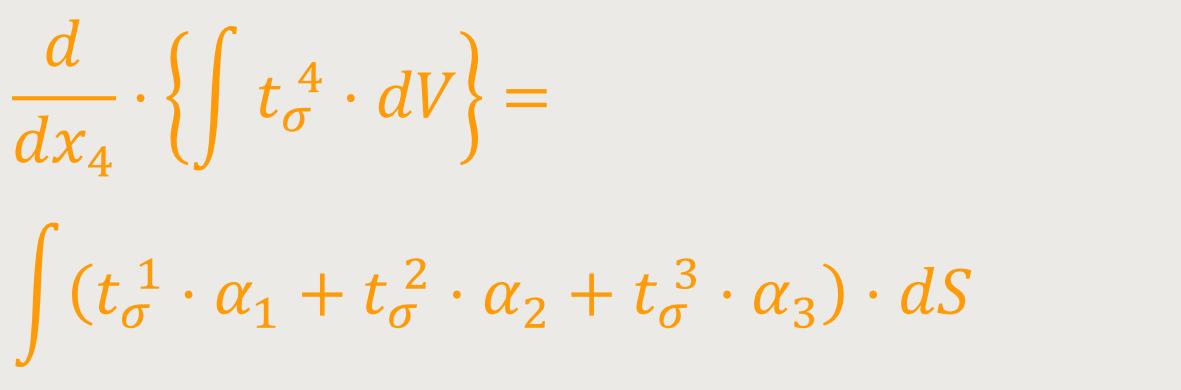
Wobei α₁, α₂, α₃ der Richtungs­kosinus der nach innen gerich­teten Normale eines Flächen­elementes der Begrenzung von der Größe dS (im Sinne der euklidischen Geometrie) bedeuten. Man erkennt hierin den Ausdruck der Erhaltungs­sätze in üblicher Fassung. Die Größen t_σ^α bezeichnet man als die „Energie­komponenten” des Gravi­tations­feldes.

Einstein gab die Gleichungen (47) noch in einer dritten Form an, die für den Sachverhalt besonders dienlich wäre. Durch Multi­plikation der Feld­gleichungen (47) mit g^νσ ergeben sich diese in der „gemischten” Form. Beachtet man, dass

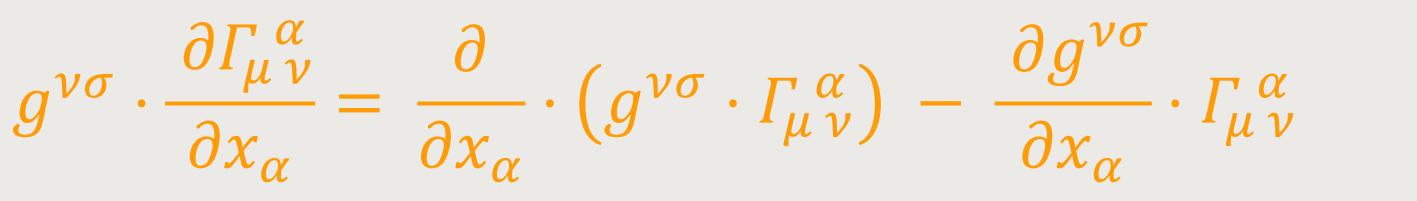
welche Größe wegen (34) gleich

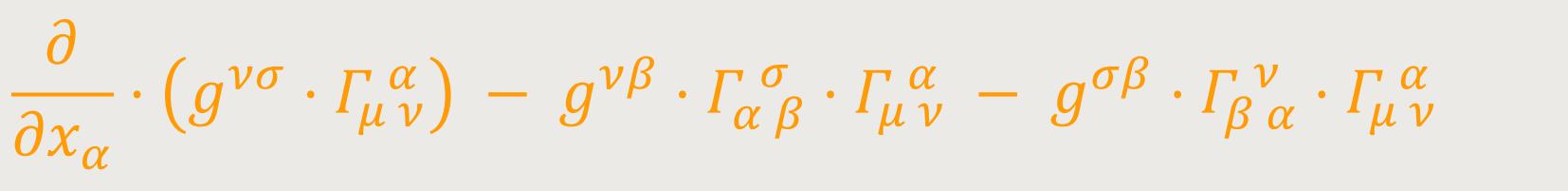
oder (nach geänderter Benennung der Summations­indizes) gleich ist

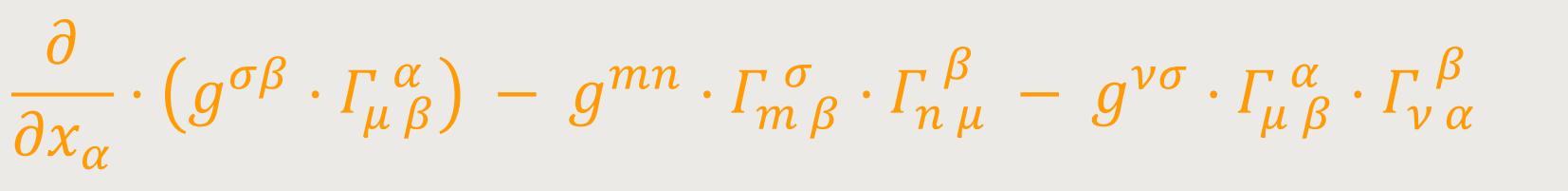
Das dritte Glied dieses Ausdrucks hebt sich weg gegen das aus dem zweiten Glied der Feld­gleichungen (47) entstehende. An Stelle des zweiten Gliedes dieses Ausdrucks lässt sich nach Beziehung: (50)

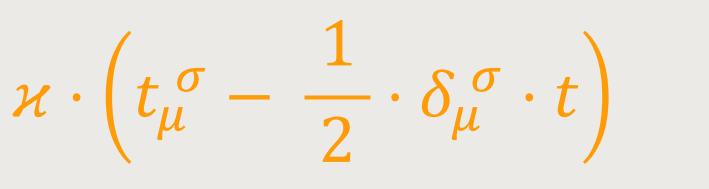
setzen (t = t_α^α). Man erhält also an Stelle der Gleichungen (47): (51)

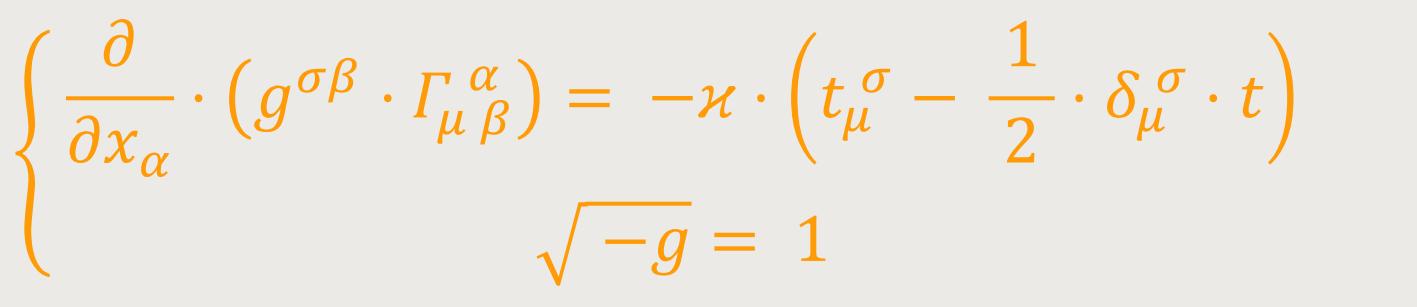
§ 16. Allgemeine Fassung der Feldgleichungen der Gravitation.

Die im vorigen Para­graphen aufge­stellten Feld­gleichungen für materie­freie Räume sind mit der Feld­gleichung

der Newtonschen Theorie zu vergleichen. Es muss die Gleichung heraus­gestellt werden, welche der Poisson-Gleichung

entspricht, wobei ϱ die Dichte der Materie bedeutet.

Die Spezielle Relativi­täts­theorie hat zu dem Ergebnis geführt, dass die träge Masse nichts anderes ist als Energie, welche ihren voll­ständigen mathe­matischen Ausdruck in einem symmetrischen Tensor zweiten Ranges, dem Energie­tensor, findet. Einstein führte daher auch in der Allgemeinen Relativi­täts­theorie einen Energie­tensor der Materie T_σ^α ein, der wie die Energie­kompo­nenten t_σ^α₁ [Gleichungen (49) und (59)] des Gravi­tations­feldes gemischten Charakter hat, aber zu einem symmetrischen kovarianten Tensor gehören wird.

Wie dieser Energie­tensor (entspre­chend der Dichte ϱ in der Poisson-Gleichung) in die Feld­gleichungen der Gravi­tation einzu­führen ist, beschreibt das Gleichungs­system (51). Betrachtet man nämlich ein voll­ständiges System (z.B. das Sonnen­system), so wird die Gesamt­masse des Systems, also auch seine gesamte gravitierende Wirkung, von der Gesamt­energie des Systems, also von der ponderablen und Gravi­tations­energie zusammen, abhängen. Dies wird sich dadurch aus­drücken lassen, dass man in (51) an Stelle der Energie­komponenten t_μ^σ des Gravi­tations­feldes allein die Summen t_μ^σ + T_μ^σ der Energie­kompo­nenten von Materie und Gravi­tations­feld ein­führt. Man erhält so statt (51) folgende Tensor­gleichung: (52)

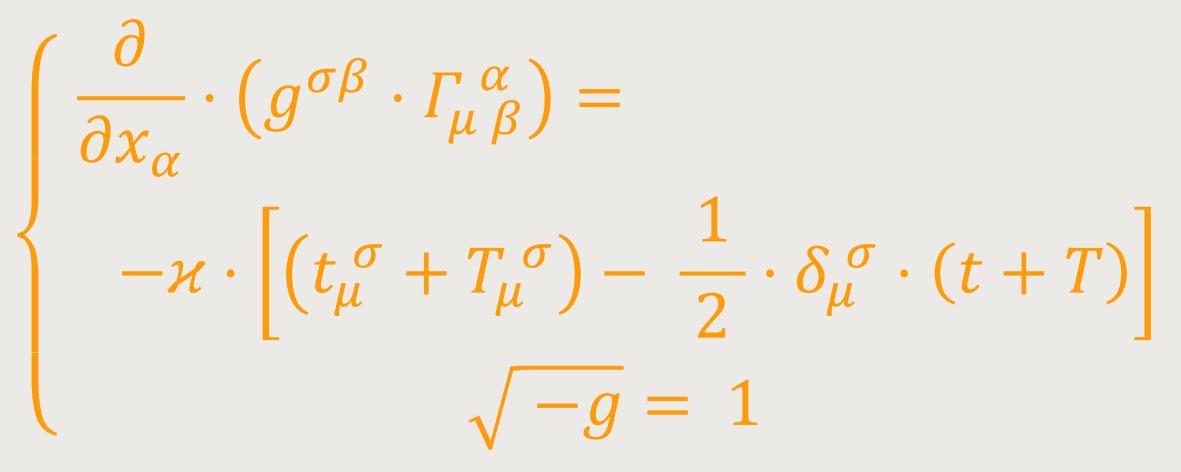
Wobei T = T_μ^μ gesetzt ist (Lauescher Skalar). Dies sind die gesuchten all­gemeinen Feld­gleichungen der Gravi­tation in gemischter Form. An Stelle von (47) ergibt sich daraus rück­wärts folgendes System: (53)

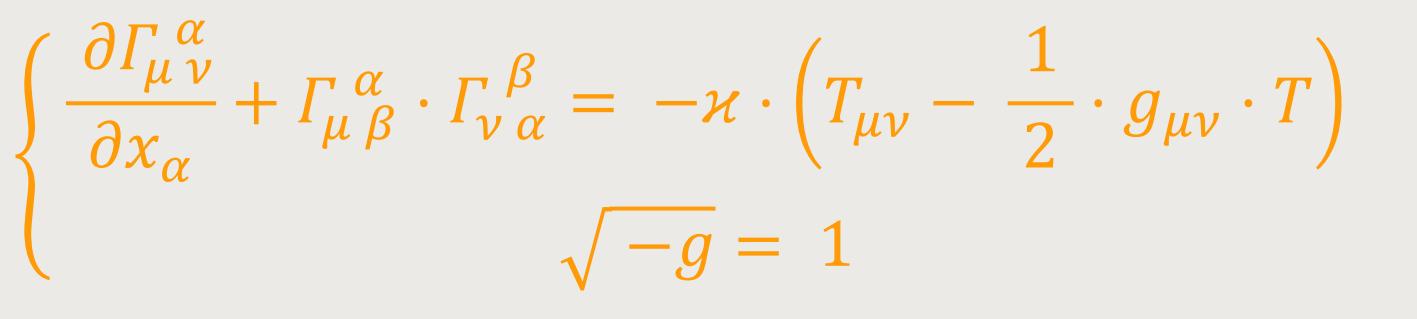
Einstein machte die Einschrän­kung, dass diese Einfüh­rung des Energie­tensors der Materie durch das Relativi­täts­postulat allein nicht gerecht­fertigt wird. Deshalb wurde sie weiter oben aus der Forderung abge­leitet, dass die Energie des Gravi­tations­feldes in gleicher Weise gravi­tierend wirken soll, wie jegliche anders geartete Energie. Der über­zeugendste Grund für die Wahl der vor­stehenden Gleichungen liegt aber darin, dass sie zur Folge haben, dass für die Kompo­nenten der Total­energie Erhaltungs­gleichungen (des Impulses und der Energie) gelten, welche den Gleichungen (49) und (49a) genau ent­sprechen. Dies soll im Folgenden dargelegt werden.

§ 17. Die Erhaltungssätze im allgemeinen Falle.

Die Gleichung (52) lässt sich leicht so umzuformen, dass auf der rechten Seite das zweite Glied weg­fällt. Man verjünge (52) nach den Indizes μ und σ und subtrahiere die so erhaltene Gleichung, mit 1/2 δ_μ^σ multi­plizierte Gleichung von (52). Es ergibt sich daraus: (52a)

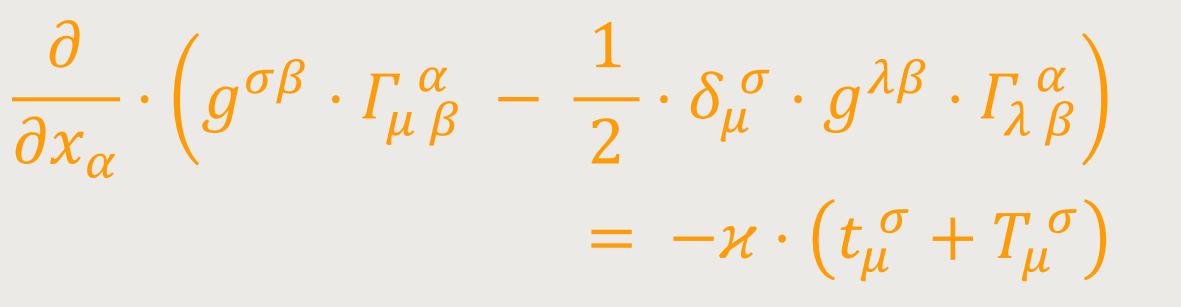
An dieser Gleichung wird die Operation ∂/∂x₀ gebildet. Folglich ist:

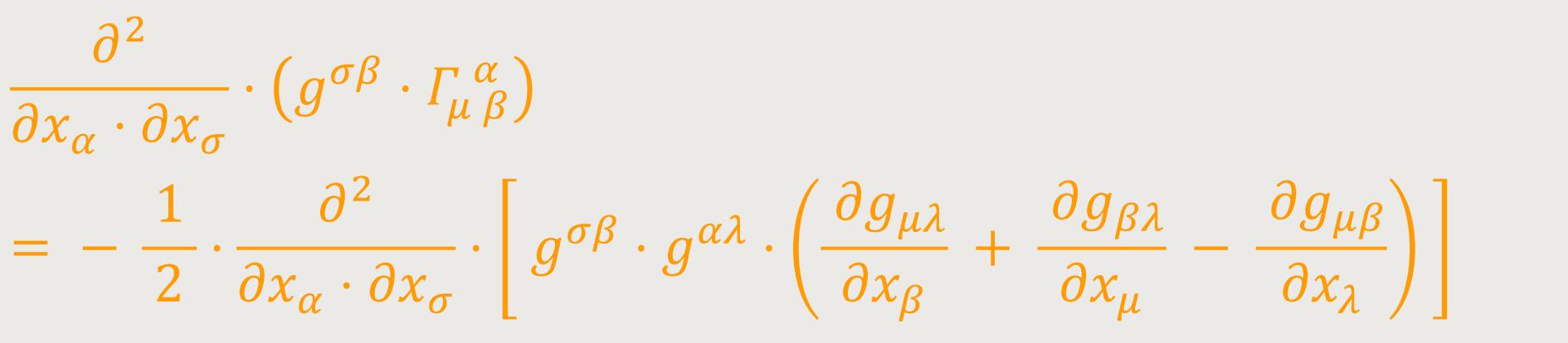
Das erste und das dritte Glied der runden Klammer liefern Beträge, die einander weg­heben, wie man erkennt, wenn im Betrag des dritten Gliedes die Summations­indizes α und σ einer­seits, sowie β und λ anderer­seits ver­tauscht. Das zweite Glied lässt sich nach (31) umformen, so dass man erhält: (54)

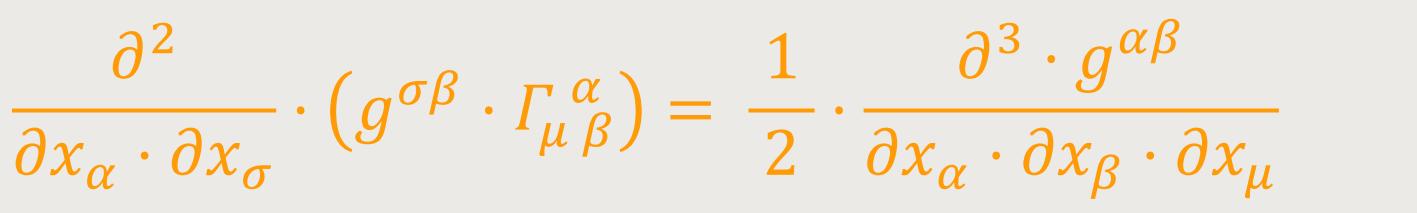
Das zweite Glied der linken Seite von (52a) liefert zunächst

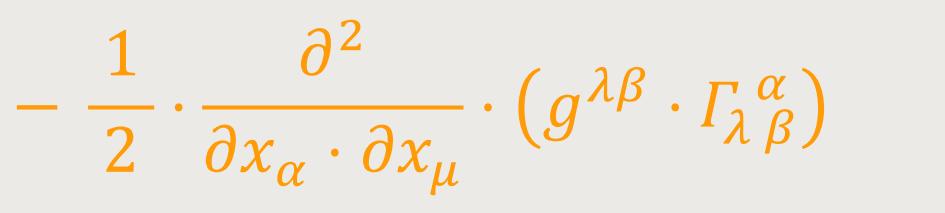
oder

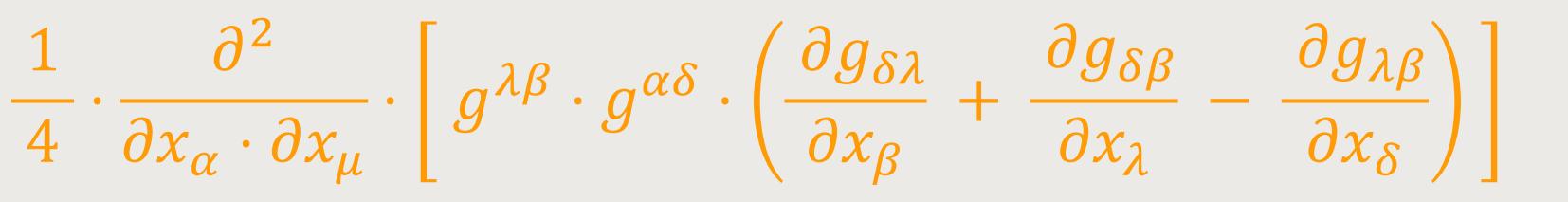
Das vom letzten Glied der runden Klammer herrührende Glied ver­schwindet wegen (29) bei der von uns getroffenen Koordinaten­wahl. Die beiden anderen lassen sich zusammen­fassen und liefern wegen (31) zusammen

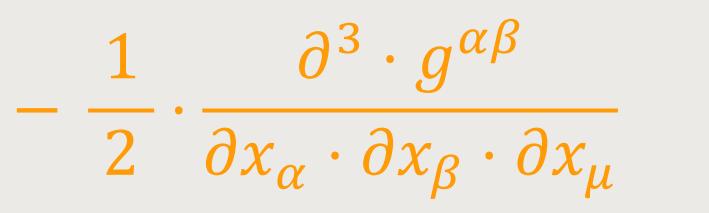
so dass mit Rück­sicht auf (54) folgende Identität besteht: (55)

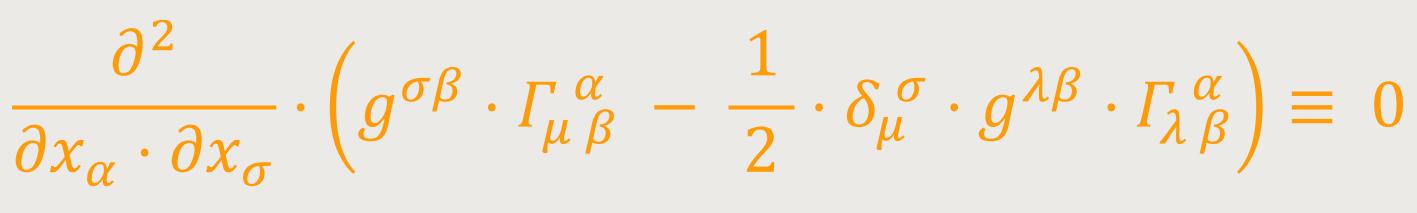
Aus (55) und (52a) folgt: (56)

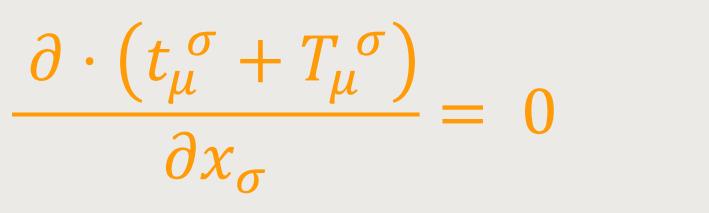
Aus den erhaltenen Feld­gleichungen der Gravi­tation geht also hervor, dass den Erhaltungs­sätzen des Impulses und der Energie Genüge geleistet ist. Man erkennt diese am ehesten in Ver­bindung mit der Betrach­tung, die zur Gleichung (49a) führt. Nur hat man hier an Stelle der Energie­kompo­nenten t_μ^σ des Gravi­tations­feldes die Gesamt­energie­kompo­nenten von Materie und Gravi­tations­feld einzu­führen.

§ 18. Der Impuls­energie­satz für die Materie als Folge der Feld­gleichungen.

Multipliziert man (53) mit ∂g^μν/∂x₀, so erhält man gemäß dem in §15 eingeschla­genen Weg mit Rück­sicht auf das Ver­schwinden von

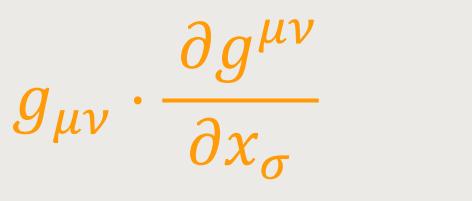
die Gleichung

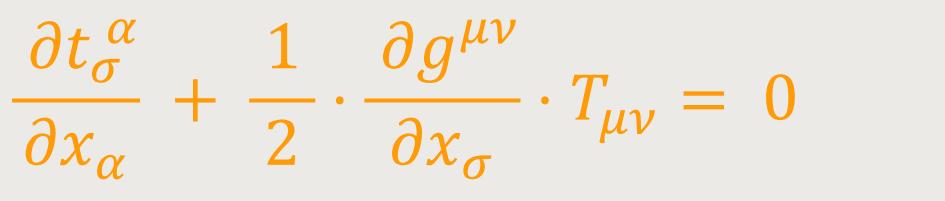
oder mit Rücksicht auf (56): (57)

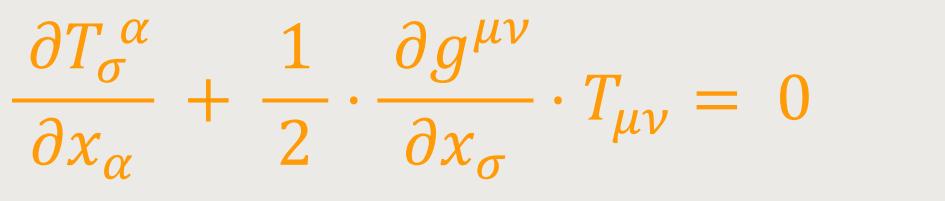
Ein Vergleich mit (41b) zeigt, dass diese Gleichung bei der getroffenen Wahl für das Koordi­naten­system nichts anderes aussagt, als das Ver­schwinden der Divergenz des Tensors der Energie­kompo­nenten der Materie. Physika­lisch zeigt das Auftreten des zweiten Gliedes der linken Seite, das für die Materie allein Erhaltungs­sätze des Impulses und der Energie im eigent­lichen Sinne nicht, bzw. nur dann gelten, wenn die g^μν konstant sind, das heißt wenn die Feld­stärken der Gravi­tation ver­schwinden. Dieses zweite Glied ist ein Ausdruck für Impuls und Energie, welche pro Volumen und Zeit­einheit vom Gravi­tations­feld auf die Materie über­tragen werden. Dies tritt noch klarer hervor, wenn man statt (57) im Sinne von (41) wie folgt schreibt: (57a)

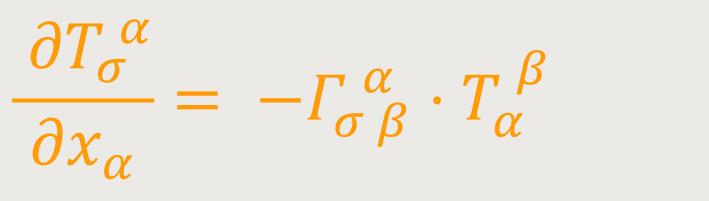
Die rechte Seite drückt die energetische Einwirkung des Gravitationsfeldes auf die Materie aus.

Die Feldgleichungen der Gravi­tation enthalten also gleich­zeitig vier Bedingungen, welchen der materielle Vorgang zu genügen hat. Sie liefern die Gleichungen des materiellen Vorgangs voll­ständig, wenn letzterer durch vier von­einander unab­hängige Differen­tial­gleichungen charakte­risierbar ist.

Was es im Detail mit den „materiellen” Vorgängen auf sich hat, schließt sich im nächsten Teil an.

⇦ Kapitel Kapitel ⇨