Laut Einstein versetzen uns die im Teil B entwickelten mathe­matischen Hilfs­mittel in die Lage, die physika­lischen Gesetze der Materie (Hydro­dynamik, Maxwellsche Elektro­dynamik), wie sie in der Speziellen Relativi­täts­theorie bereits formuliert vor­lagen, so zu verall­gemeinern, dass sie in die Allgemeine Relativi­täts­theorie hinein­passen. Das all­gemeine Relativi­täts­prinzip führt zwar zu keiner weiteren Einschrän­kung der Möglich­keiten, dennoch ver­mittelt es den Ein­fluss des Gravi­tations­feldes auf alle Prozesse exakt, ohne dass irgend­welche neue Hypothese einge­führt werden müsste.

Diese Sachlage bringt es mit sich, dass über die physika­lische Natur der Materie (im engeren Sinne) nicht zwingend bestimmte Voraus­setzungen einge­führt werden müssen. Insbesondere kann die Frage offen bleiben, ob die Theorie des elektro­magnetischen Feldes und des Gravi­tations­feldes zusammen eine hinreichende Basis für die Theorie der Materie liefern oder nicht. Das allgemeine Relativi­täts­postulat kann hierzu im Prinzip nichts beitragen. Es muss sich bei dem Ausbau der Theorie zeigen, ob Elektro­magnetik und Gravi­tations­lehre zusammen leisten können, was ersterer allein nicht gelingen will.

§19. Eulersche Gleichungen für reibungslose adiabatische Flüssigkeiten.

Es seien p und ϱ zwei Skalare, bei denen es sich um den Druck und die Dichte einer Flüssig­keit handelt, wobei zwischen ihnen eine Gleichung bestehe. Der kontra­variante symme­trische Tensor sei der kontra­variante Energie­tensor der Flüssig­keit: (58)

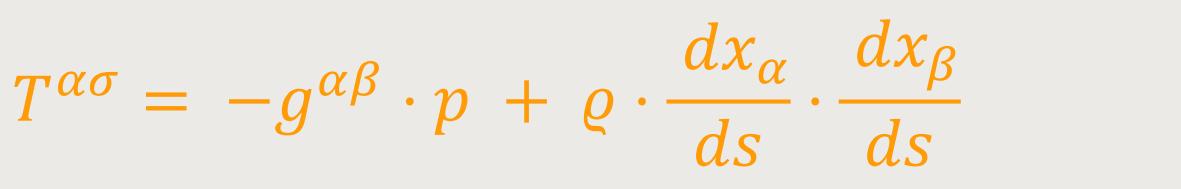
Zu ihm gehört der kovariante Tensor: (58a)

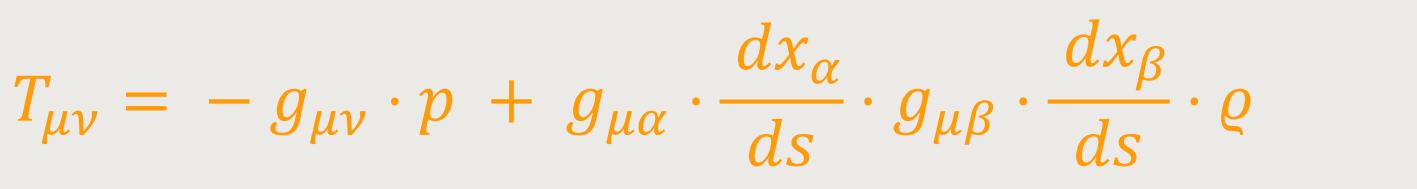
sowie der gemischte Tensor: (58b)

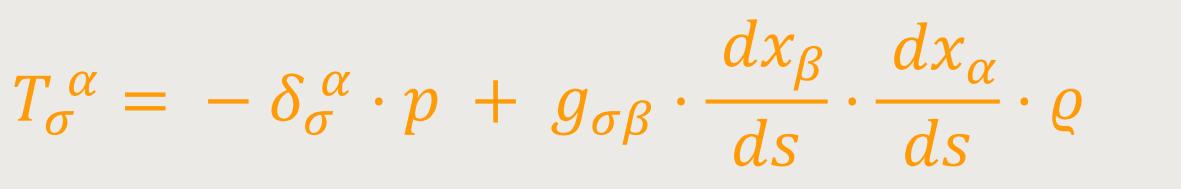
Einstein ergänzt hierzu, dass für einen mit­bewegten Beobachter, der im unendlich Kleinen ein Bezugs­system im Sinne der Speziellen Relativi­täts­theorie benutzt, die Energie­dichte T₄⁴ gleich ϱ − p ist.

Setzt man die rechte Seite von (58b) in (57a) ein, so erhält man die Eulerschen hydro­dynamischen Gleichungen der Allgemeinen Relativi­täts­theorie. Diese lösen das Bewegungs­problem im Prinzip voll­ständig. Denn die vier Gleichungen (57a) zusammen mit der gegebenen Gleichung zwischen p und ϱ und der Gleichung

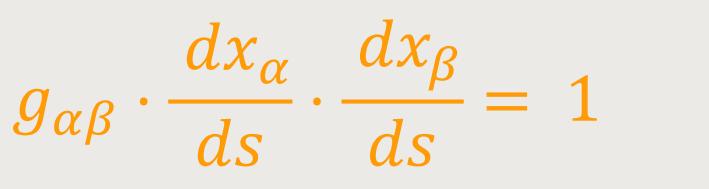
genügen bei gegebenen g_αβ zur Bestimmung der folgenden 6 Unbekannten:

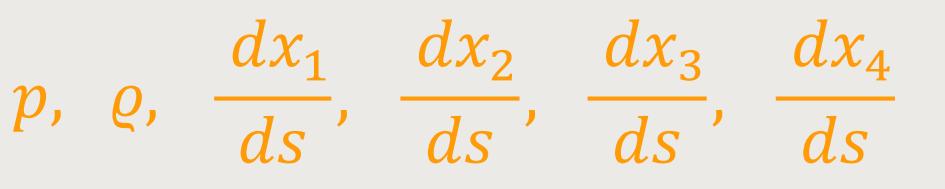
Sind auch die g_μν unbekannt, so kommen hierzu noch die Gleichungen (53). Dies sind 11 Gleichungen zur Bestimmung der 10 Funktionen g_μν, so dass diese über­bestimmt scheinen. Es ist indessen zu beachten, dass die Gleichungen (57a) in den Gleichungen (53) bereits enthalten sind, so dass letztere nur mehr 7 unabhängige Gleichungen repräsen­tieren. Diese Unbestimmt­heit hat ihren Grund darin, dass die weit­gehende Freiheit in der Wahl der Koordi­naten es mit sich bringt, dass das Problem mathe­matisch in dem Maße unbestimmt bleibt, dass drei der Raum­funktionen beliebig gewählt werden können.

Hierzu ergänzt Einstein, dass bei Verzicht auf die Koordi­naten­wahl gemäß g = −1 vier Raum­funktionen frei wähl­bar blieben, entspre­chend den vier willkür­lichen Funktionen, über die man bei der Koordi­naten­wahl frei verfügen kann.

§ 20. Maxwellsche elektromagnetische Feldgleichungen für das Vakuum.

Es seien φ_ν die Kompo­nenten eines kovarianten Vierer­vektors, und zwar des Vierer­vektors des elektro­magne­tischen Poten­tials. Aus ihnen bildet man gemäß (36) die Kompo­nenten F_ϱσ des kovarianten Sechser­vektors des elektro­magnetischen Feldes gemäß folgendem Gleichungs­system: (59)

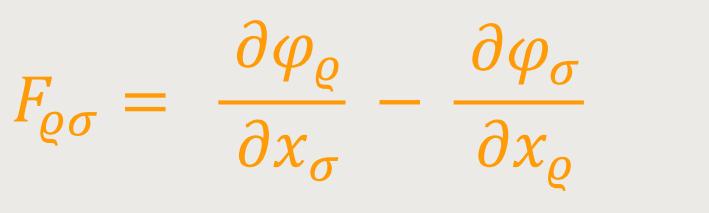
Aus (59) folgt, dass das folgendes Gleichungs­system erfüllt ist: (60)

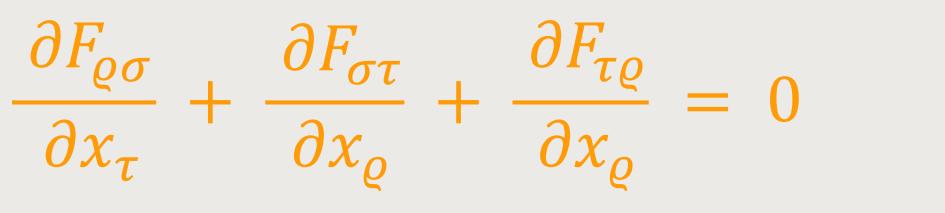
Wobei dessen linke Seite gemäß (37) ein anti­symmetrischer Tensor dritten Ranges ist. Das System (60) enthält also im Wesent­lichen 4 Gleichungen, die ausge­schrieben wie folgt lauten: (60a)

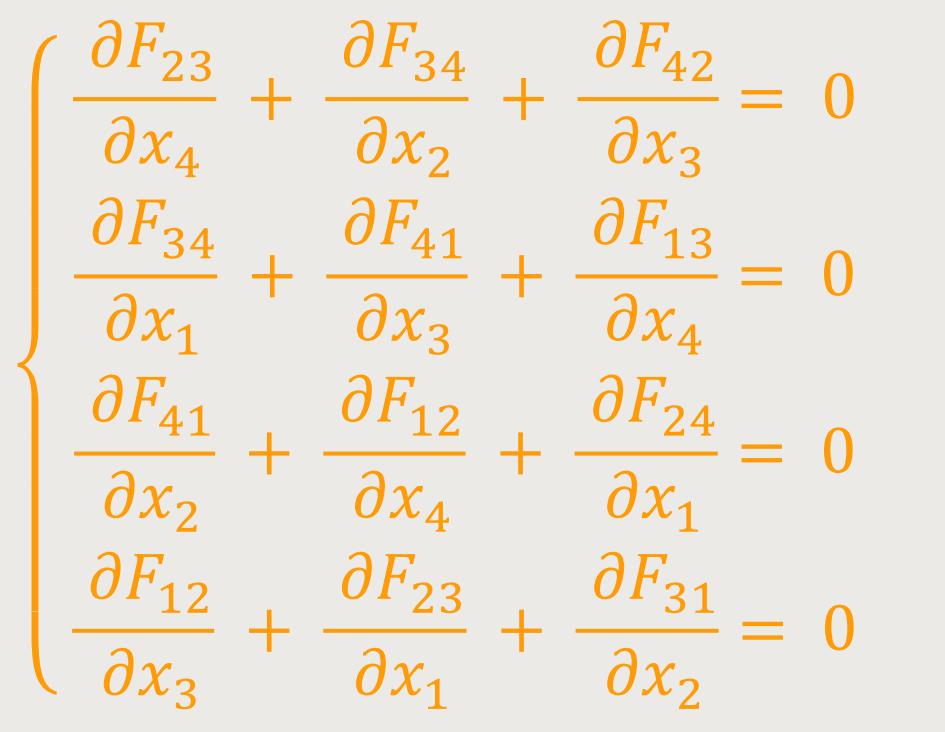
Dieses Gleichungs­system ent­spricht dem zweiten Gleichungs­system Maxwells. Nach Einsteins Worten würde man dies sofort erkennen, wenn man folgendes festlegt: (61)

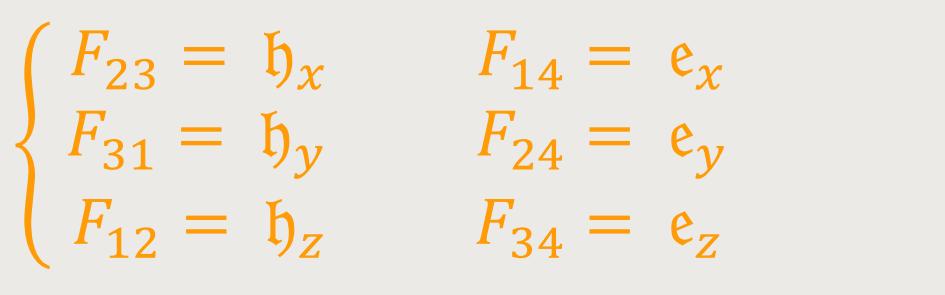
Dann kann man statt (60a) in der üblichen Schreib­weise der 3-dimen­sionalen Vektor­analyse fest­legen: (60b)

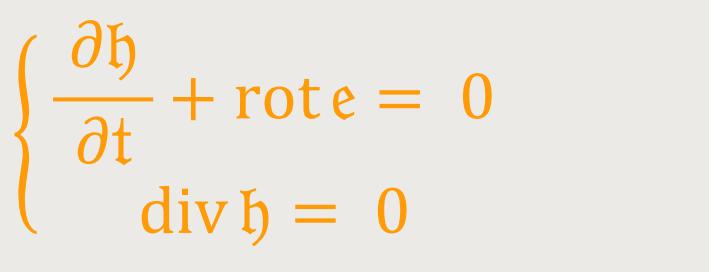
Das erste Maxwellsche System erhält man durch Verallge­meinerung der von Minkowski ange­gebenen Form. Nun führt man den zu F_αβ gehörenden kontra­varianten Sechser­vektor ein: (62)

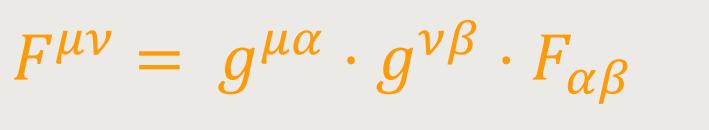
Sowie den kontra­varianten Vierer­vektor J ^μ der elektrischen Vakuum­strom­dichte. Dann lässt sich mit Rück­sicht auf (40) gegen­über beliebigen Substitu­tionen von der Deter­minante 1 (gemäß der getroffenen Koordi­naten­wahl) folgendes invariante Gleichungs­system fest­legen: (63)

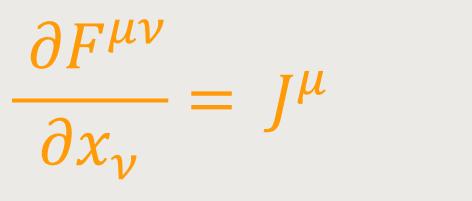
Legt man nämlich folgendes fest: (64)

Wobei dessen Größen im Spezial­fall der Speziellen Relativi­täts­theorie den Größen h_x ... e_z ent­sprechen, und außerdem:

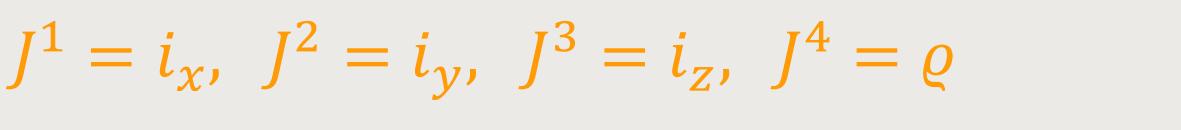
So erhält man an Stelle von (63): (63a)

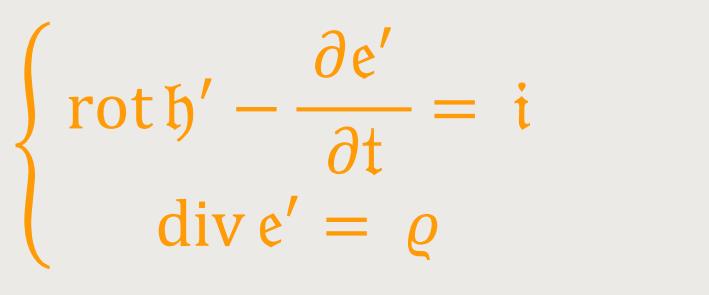
Die Gleichungen (60), (62) und (63) bilden also die Verallge­meinerung der Maxwellschen Feld­gleichungen des Vakuums bei der im vorliegenden Fall bezüg­lich der Koordinaten­wahl getroffenen Fest­setzung.

Die Energie­komponenten des elektro­magnetischen Feldes. Man bildet das innere Produkt: (65)

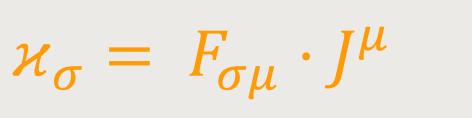
Seine Komponenten lauten gemäß (61) in 3-dimen­sionaler Schreib­weise: (65a)

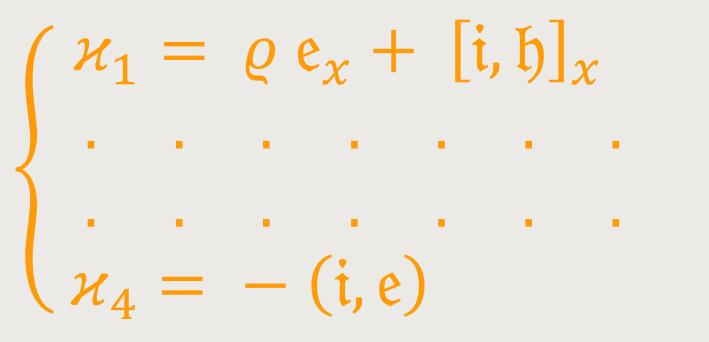
Es ist ϰ_σ ein kovarianter Vierer­vektor, dessen Kompo­nenten gleich sind mit dem negativen Impuls bzw. der Energie, welche pro Zeit- und Volumen­einheit auf das elektro­magne­tische Feld von den elek­trischen Massen über­tragen werden. Sind die elektrischen Massen frei, das heißt stehen sie allein unter dem Einfluss des elektro­magne­tischen Feldes, so wird der kovariante Vierer­vektor ϰ_σ verschwinden.

Um die Energiekomponenten T_σ^ν des elektro­magne­tischen Feldes zu erhalten, muss der Gleichung ϰ_σ = 0 nur die Gestalt der Gleichung (57) gegeben werden. Aus (63) und (65) ergibt sich zunächst:

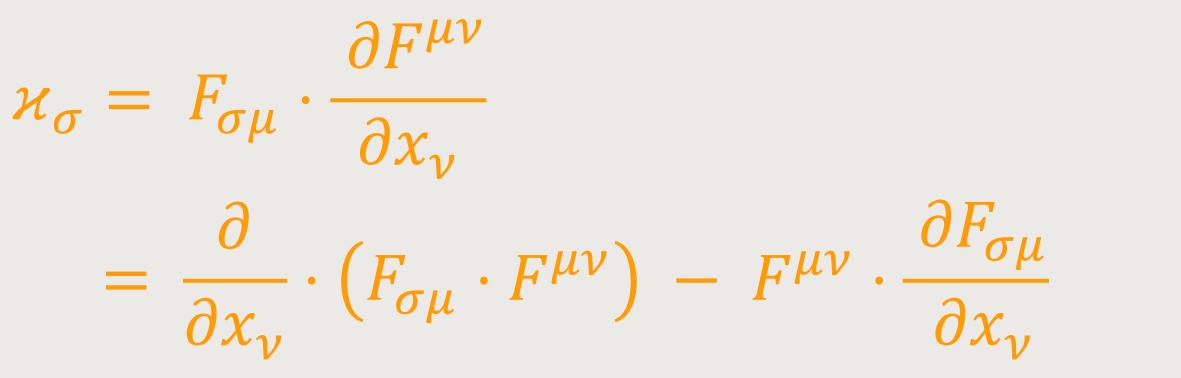
Das zweite Glied der rechten Seite ermöglicht auf Grund­lage von (60) die Umformung:

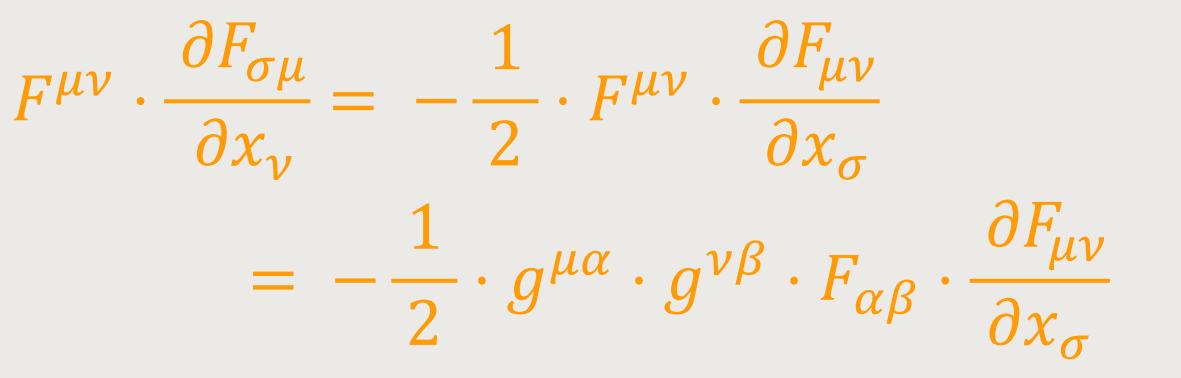
Dessen letzter Ausdruck kann aus Symmetrie­gründen auch wie folgt geschrieben werden:

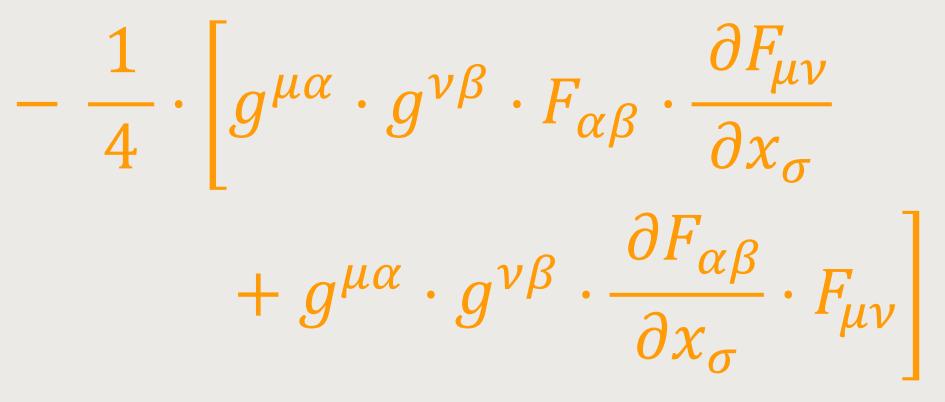
Hierfür aber lässt sich auch festlegen:

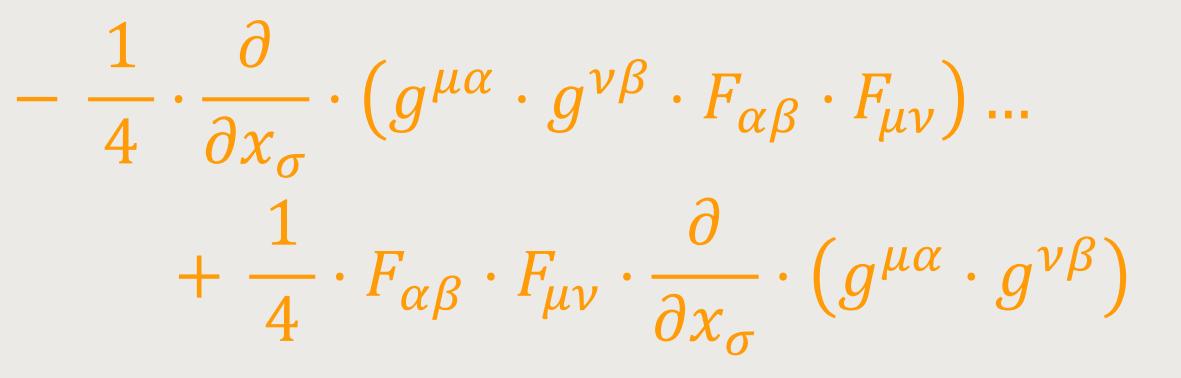
Das erste dieser Glieder lautet in gekürzter Schreib­weise:

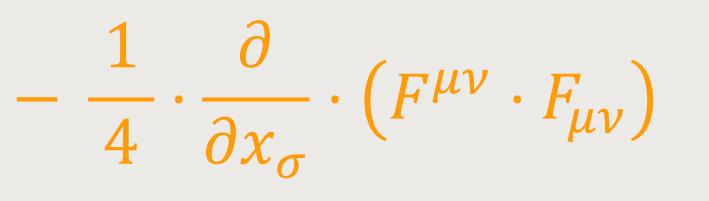
Das zweite Gleid ergibt nach Ausführung der Differentiation nach einiger Umformung:

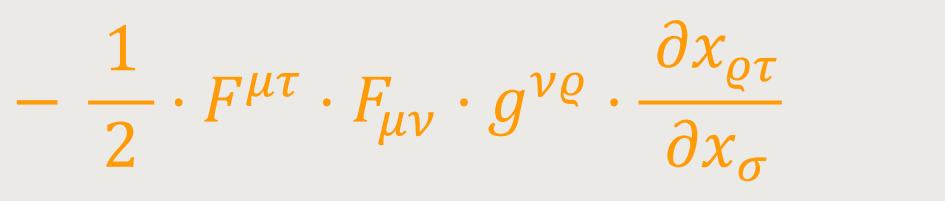
Fasst man alle drei berechneten Glieder zusammen, so erhält man folgende Relation: (66)

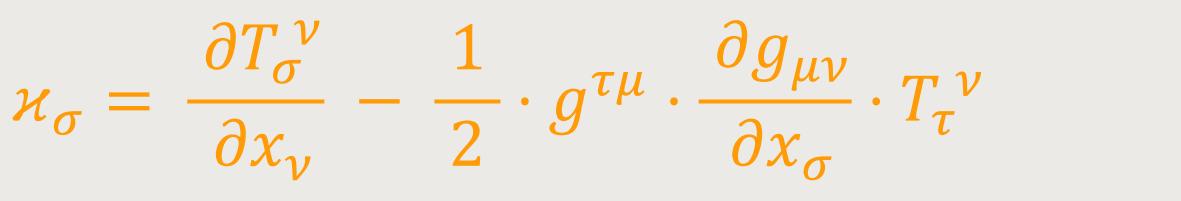
Wobei sich ergibt: (66a)

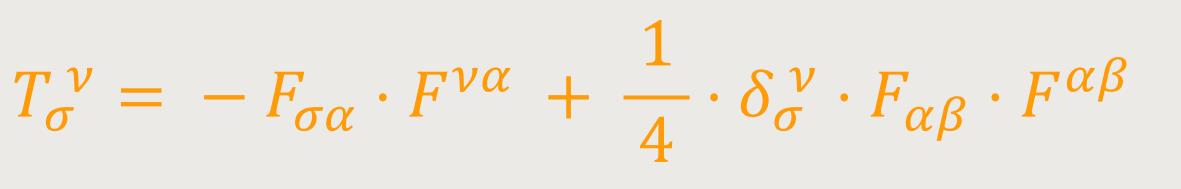
Die Gleichung (66) ist für unter­schiedliche ϰ_σ wegen (30) mit (57) bzw. (57a) gleich­wertig. Es sind also die T_σ^ν die Energie­komponenten des elektro­magne­tischen Feldes. Mithilfe von (61) und (64) lässt sich leicht zeigen, dass diese Energie­kompo­nenten des elektro­magne­tischen Feldes im Fall der Speziellen Relativi­täts­theorie die wohl­bekannten Maxwell-Pointingschen Ausdrücke ergeben.

Es wurden also die grund­legenden Gesetze abgeleitet, welche für das Gravi­tations­feld und die Materie maßgeblich sind, indem man sich konsequent eines Koordi­naten­systems bedient hat, für welches √−g = 1 gilt. Man erhält dadurch eine wesent­liche Verein­fachung der Formeln und Rechnungen, ohne dass man auf die Forderung der all­gemeinen Kovarianz ver­zichten muss. Denn es wurden die Gleichungen durch Speziali­sierung des Koordi­naten­systems aus allgemein kovarianten Gleichungen abgeleitet.

Immerhin sei aus Einsteins Sicht die Frage nicht ohne formales Interesse, ob bei entspre­chend verall­gemeinerter Definition der Energie­kompo­nenten des Gravi­tations­feldes und der Materie auch ohne Speziali­sierung des Koordi­naten­systems Erhaltungs­sätze von der Gestalt der Gleichung (56) sowie Feld­gleichungen der Gravitation von der Art der Gleichungen (52) und (52a) gelten, und zwar in der Weise, dass links eine Divergenz (im gewöhn­lichen Sinne), dagegen rechts die Summe der Energie­komponenten der Materie und der Gravi­tation steht. Einstein habe heraus­gefunden, dass tatsäch­lich beides der Fall ist. Doch er glaubte, dass eine Darlegung seiner ziemlich umfang­reichen Betrach­tungen über diesen Sach­verhalt sich nicht lohnen würde, da sich inhalt­lich nicht Neues dabei ergibt.

§ 21. Newtons Theorie als erste Näherung.

Wie schon mehrfach erwähnt, ist die Spezielle Relativi­täts­theorie ein Spezial­fall der Allgemeinen und dadurch charakte­risiert, dass die g_μν die konstanten Werte (4) haben. Dies bedeutet nach dem bisher Behandelten eine völlige Vernach­lässigung der Gravitations­wirkungen. Eine mehr an der Wirklich­keit orientierte Approxi­mation erhält man, indem man den Fall betrachtet, bei dem die g_μν von den Werten (4) nur um (gegen 1) kleine Größen abweichen, wobei kleine Größen zweiten und höheren Grades vernach­lässigt werden. Das wäre ein erster Gesichts­punkt der Approximation.

Ferner soll angenommen werden, dass in dem betrachteten raum­zeitlichen Gebiet die g_μν im räumlich Unendlichen bei passender Wahl der Koordinaten den Werten (4) zustreben, das heißt man betrachtet Gravi­tations­felder, welche als aus­schließlich durch im Endlichen befind­liche Materie erzeugt betrachtet werden können.

Man könnte annehmen, dass diese Vernach­lässi­gungen auf Newtons Theorie hinführen müssten. Statt­dessen bedarf es hier­für noch der approxi­mativen Behand­lung der Grund­gleichungen nach einem zweiten Gesichts­punkt. Indem man die Bewegung eines Masse­punktes gemäß den Gleichungen (46) betrachtet. Im Fall der Speziellen Relativi­täts­theorie können folgende Komponenten beliebige Werte annehmen:

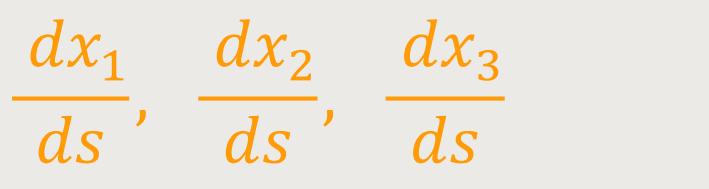
Dies bedeutet, dass beliebige Geschwindig­keiten auftreten können,

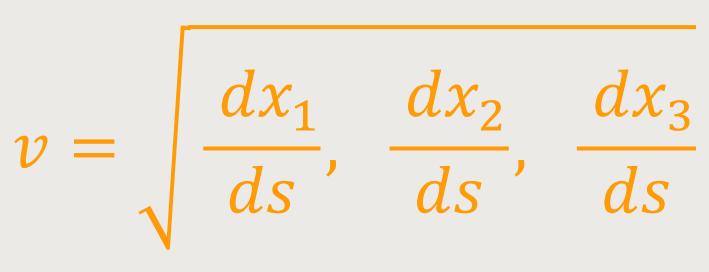
die kleiner sind als die Vakuum­licht­geschwin­dig­keit (v < 1). Will man sich auf den ausschließ­lich unserer Erfahrung beruhenden Fall beschränken, dass v gegen die Licht­geschwin­dig­keit klein ist, so bedeutet dies, dass nach­folgende Kompo­nenten als kleine Größen zu behandeln sind:

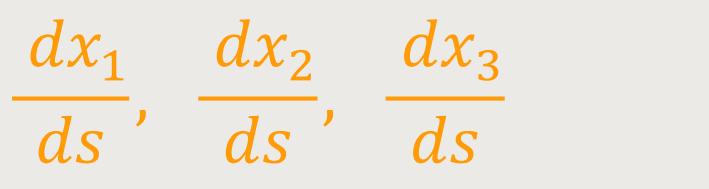
Während dx₄ /ds bis auf Größen zweiter Ordnung den Wert 1 hat. Dies ist der zweite Gesichts­punkt der Approximation.

Nun gilt zu beachten, dass nach dem ersten Gesichts­punkt der Approxi­mation die Größen Γ_μ^τ_ν alle kleine Größen mindestens erster Ordnung sind. Ein Blick auf (46) zeigt also, dass in dieser Gleichung gemäß dem zweiten Gesichts­punkt der Approxi­mation nur Glieder zu berück­sichtigen sind, für welche μ = ν = 4 gilt. Bei Beschrän­kung auf Glieder niedrigster Ordnung erhält man an Stelle von (46) zunächst folgende Gleichungen:

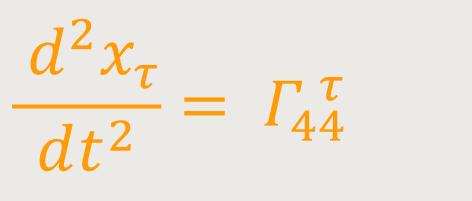
Wobei ds = dx₄ = dt fest­gelegt ist, oder unter Beschränkung auf Glieder, die nach dem ersten Gesichts­punkt der Approxi­mation erster Ordnung gilt:

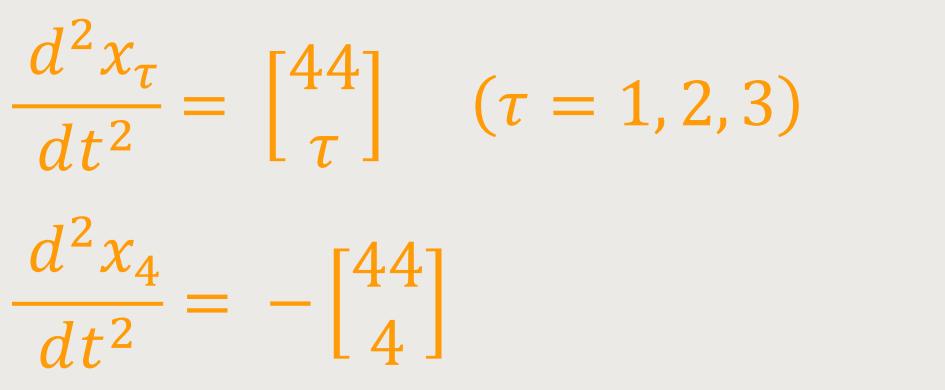
Setzt man außerdem voraus, dass das Gravi­tations­feld ein quasi statisches sei, indem man sich auf den Fall beschränkt, dass die das Gravi­tations­feld erzeugende Materie sich nur langsam (im Vergleich mit der Fort­pflanzungs­geschwin­dig­keit des Lichtes) bewegt, so kann man auf der rechten Seite Ableitungen nach der Zeit neben solchen nach den örtlichen Koordi­naten vernach­lässigen, so dass man erhält: (67)

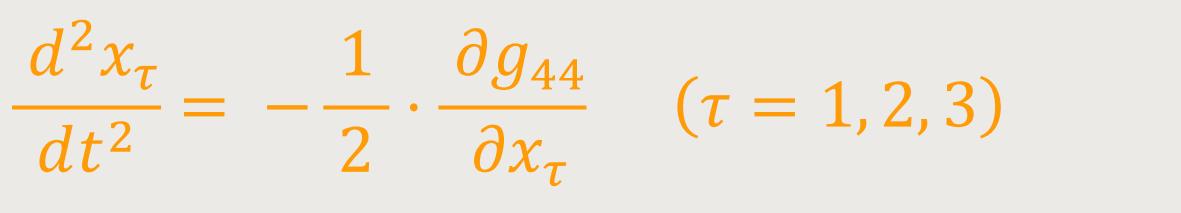
Dies ist die Bewegungs­gleichung des materiellen Punktes nach Newtons Theorie, wobei g₄₄/2 die Rolle des Gravi­tations­potentials über­nimmt. Das Merkwürdige an diesem Resultat ist, dass nur die Komponente g₄₄ des Fundamental­tensors allein in erster Näherung die Bewegung des materiellen Punktes bestimmt.

Wir wenden uns nun den Feld­gleichungen (53) zu. Dabei ist zu berück­sichtigen, dass der Energie­tensor der „Materie” fast ausschließ­lich durch die Dichte ϱ der Materie im engeren Sinne bestimmt wird, das heißt durch das zweite Glied der rechten Seite von (58) [bzw. (58a) oder (58b)]. Bildet man die uns interes­sierende Näherung, so verschwinden alle Kompo­nenten bis auf die Komponente:

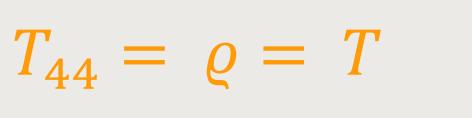
Auf der linken Seite von (53) ist das zweite Glied klein von zweiter Ordnung. Das erste Glied liefert in der uns interes­sierenden Näherung:

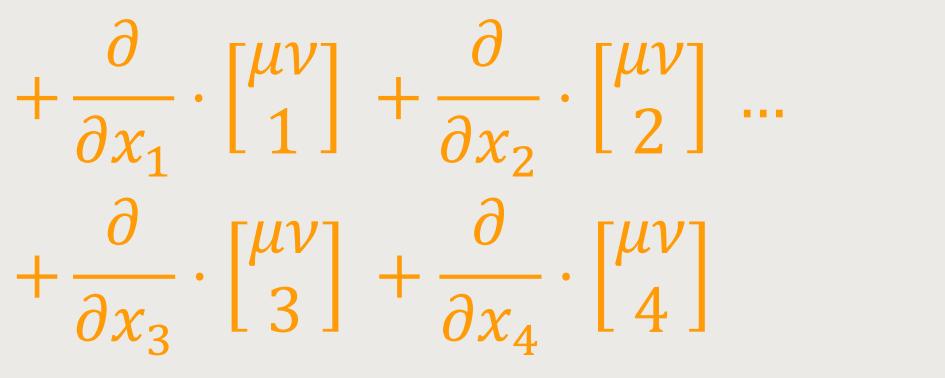
Dies liefert für μ = ν = 4 bei Weglassung von nach der Zeit differenzierten Gliedern:

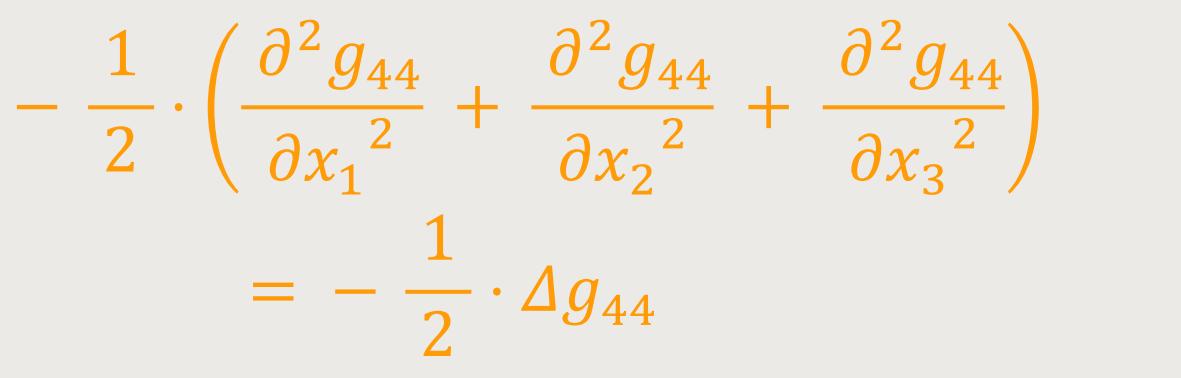
Die letzte der Gleichungen (53) liefert also: (68)

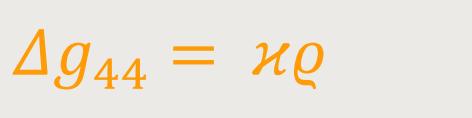
Die Gleichungen (67) und (68) zusammen sind äquivalent mit dem Newtonschen Gravi­tations­gesetz.

Für das Gravitations­potential ergibt sich nach (67) und (68) der Ausdruck: (68a)

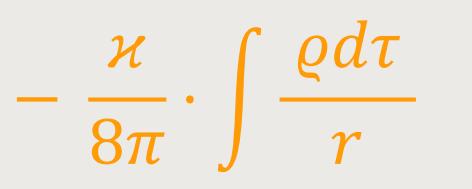
Während Newtons Theorie bei der von uns gewählten Zeit­einheit folgendes ergibt:

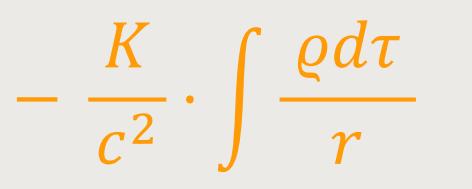
Wobei nach Einstein K die allgemein als Gravi­tations­konstante bezeichnete Konstante 6,7 · 10⁻⁸ bedeutet. Durch Vergleich ergibt sich: (69)

Hinweis: Heute schreibt man für die Gravi­tations­konstante: G = 6,67430(15) · 10⁻¹¹ m³/(kg·s²)

§ 22. Verhalten von Maßstäben und Uhren im statischen Gravitationsfeld. Krümmung der Lichtstrahlen. Perihelbewegung der Planetenbahnen.

Um die Newtonsche Theorie als erste Näherung zu erhalten, braucht man von den 10 Kompo­nenten des Gravi­tations­potentials g_μν nur g₄₄ zu berechnen, da nur diese Kompo­nente in die erste Näherung (67) der Bewegungs­gleichung des materiellen Punktes im Gravi­tations­feld eingeht. Man kann indessen schon daraus erkennen, dass noch andere Kompo­nenten der g_μν von den in (4) ange­gebenen Werten in erster Näherung abweichen müssen, dass letzteres durch die Bedingung g = −1 verlangt wird.

Für einen im Anfangs­punkt des Koordi­naten­systems befind­lichen feld­erzeugenden Massen­punkt erhält man in erster Näherung folgende radial­symmetrische Lösung: (70)

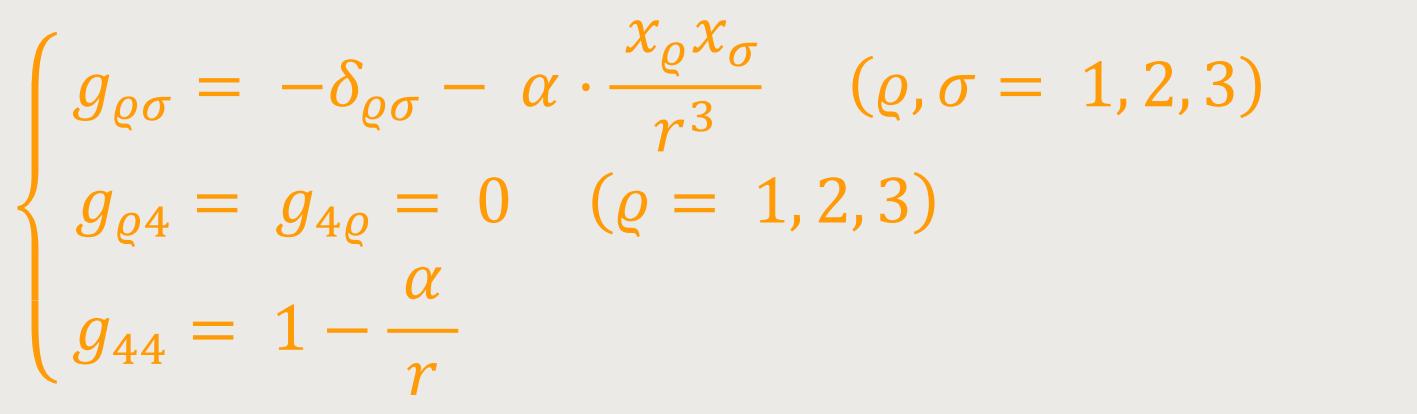
δ_ϱσ ist dabei 1 bzw. 0, je nachdem ob ϱ = 0 oder ϱ · σ.
Wobei r folgende Größe ist:

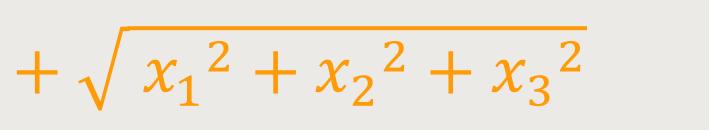
Wegen (68a) gilt für α: (70a)

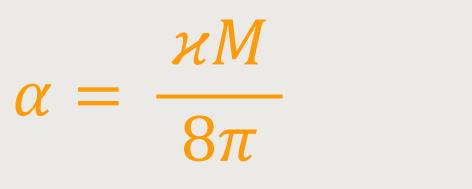
Wobei mit M die feld­erzeugende Masse bezeichnet wird. Dass durch diese Lösung die Feld­gleichungen (außerhalb der Masse) in erster Näherung erfüllt werden, sei nach Einsteins Aussage leicht zu verifizieren.

Nun gilt es, die Beeinflussung zu untersuchen, welche die metrischen Eigen­schaften des Raumes durch das Feld der Masse M erfahren. Stets gilt zwischen den „lokal” (§ 4) gemessenen Längen und Zeiten ds einer­seits und den Koordinaten­differenzen dx_ν anderer­seits folgende Beziehung:

Für einen „parallel” zur x-Achse gelegten Einheits­maßstab wäre beispiels­weise fest­zulegen:

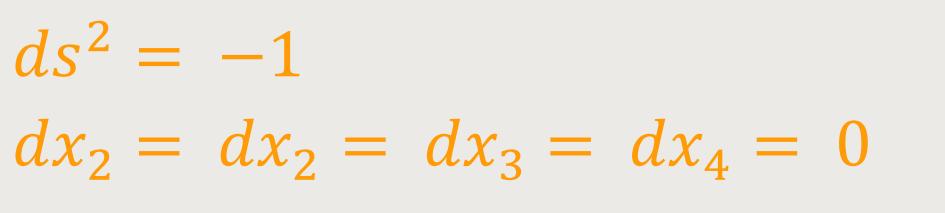
Also

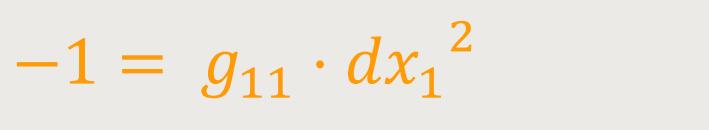
Liegt der Einheits­maßstab außerdem auf der x-Achse, so ergibt die erste der Gleichungen: (70)

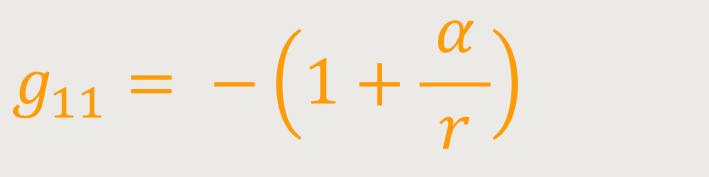
Aus beiden Relationen folgt in erster Näherung: (71)

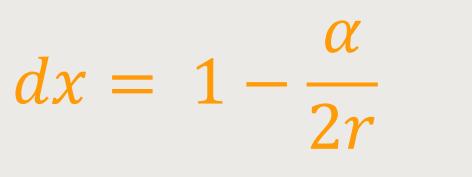
Der Einheitsmaßstab erscheint also mit Bezug auf das Koordi­naten­system mit dem ermittelten Betrag durch das Vor­handen­sein des Gravitations­feldes verkürzt, wenn er radial angelegt wird.

Analog erhält man seine Koordi­naten­länge in tangentialer Richtung, indem man beispiels­weise festlegt:

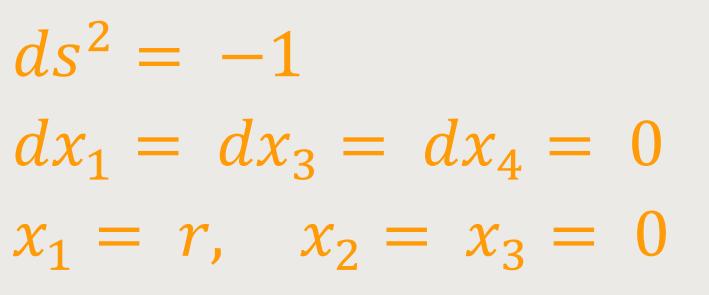
Daraus ergibt sich: (71a)

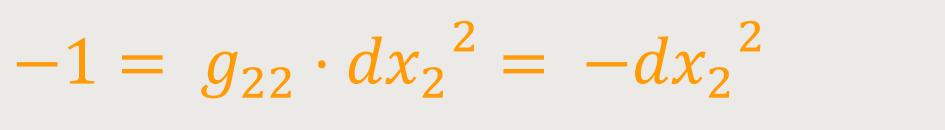
Bei tangentialer Stellung hat also das Gravi­tations­feld des Massen­punktes keinen Einfluss auf die Stablänge.

Es gilt demnach die Euklidische Geometrie im Gravi­tations­feld nicht einmal in erster Näherung, falls man ein und denselben Stab unabhängig von seinem Ort und seiner Orientierung als Realisierung derselben Strecke auffassen will. Aller­dings zeigt ein Blick auf (70a) und (69), dass die zu erwartenden Abwei­chungen viel zu gering sind, um sich bei der Vermes­sung der Erdober­fläche bemerkbar machen zu können.

Des Weiteren gilt es, ferner die auf die Zeit­koordinate unter­suchte Gang­geschwin­digkeit einer Einheits­uhr zu unter­suchen, welche in einem statischen Gravi­tations­feld ruhend angeordnet ist. Hier gilt für eine Uhr­periode:

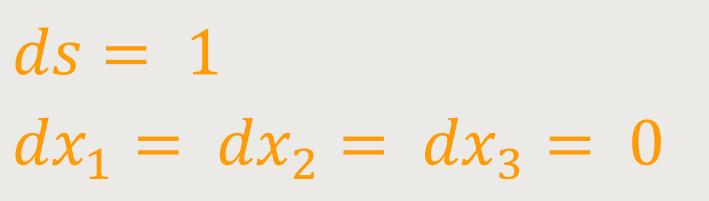
Also ist

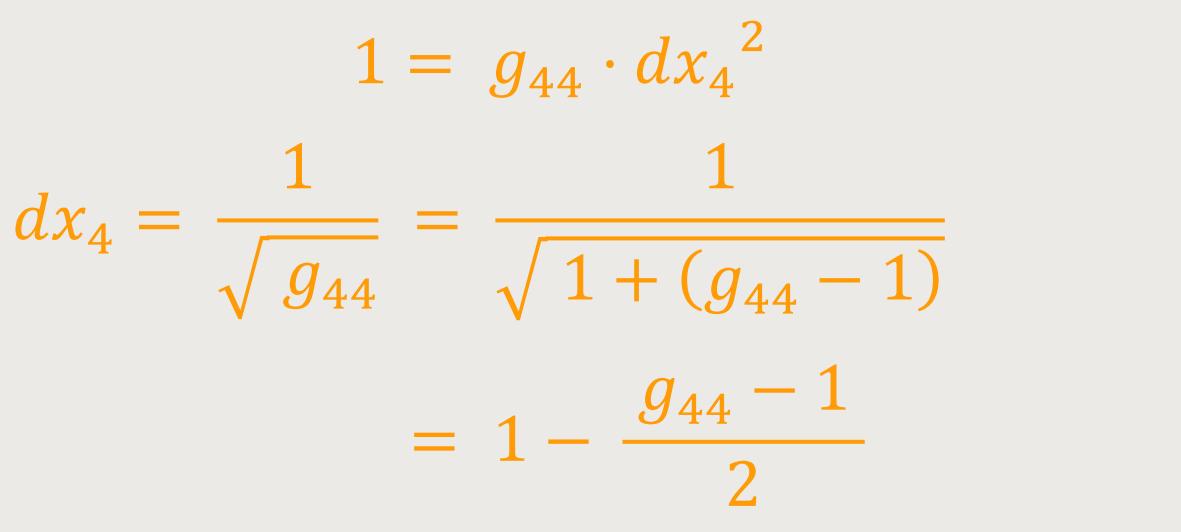
oder: (72)

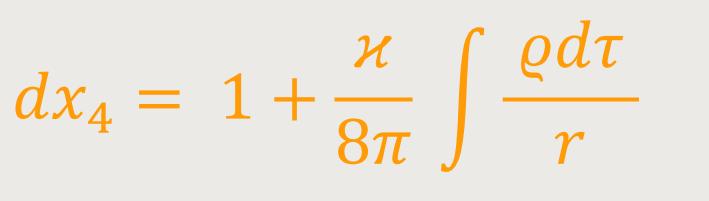
Die Uhr läuft demnach langsamer, wenn sie in der Nähe ponderabler Massen auf­gestellt ist. Es folgt daraus, dass die Spektral­linien von der Ober­fläche großer Sterne zu uns gelangenden Lichtes nach dem roten Spektralende verschoben erscheinen müssen.

Untersucht man ferner den Gang der Licht­strahlen im statischen Gravi­tations­feld, so gilt gemäß der Speziellen Relativi­täts­theorie für die Licht­geschwin­dig­keit folgende Gleichung:

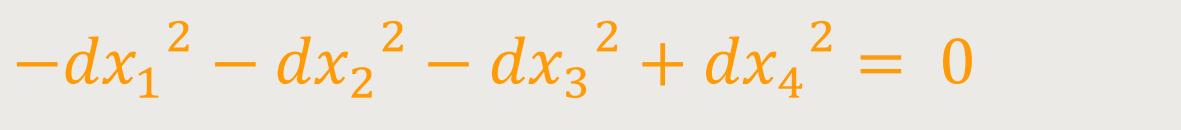
Oder gemäß der Allgemeinen Relativi­täts­theorie durch die Gleichung: (73)

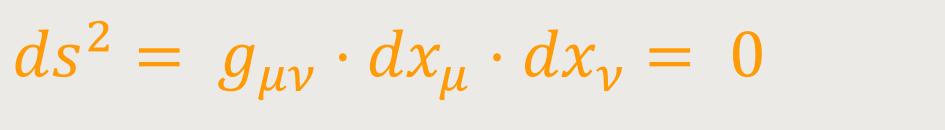
Ist die Richtung, das heißt das Verhält­nis dx₁ : dx₂ : dx₃ gegeben, so liefert die Gleichung (73) folgende Größen:

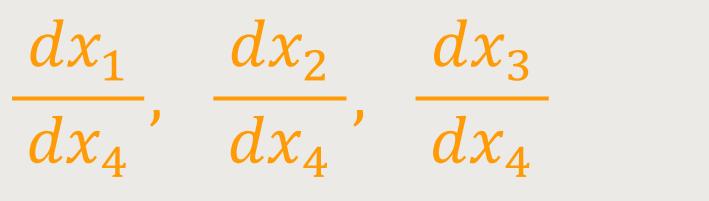
Und damit ist die Geschwindig­keit im Sinne der Euklidischen Geometrie definiert als:

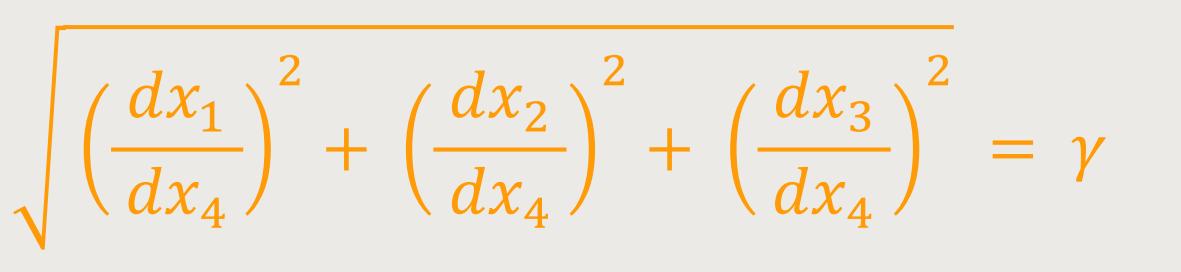
Nach Einsteins Worten ist leicht zu erkennen, dass die Licht­strahlen gekrümmt verlaufen müssen mit Bezug auf das Koordi­naten­system, falls die g_μν nicht konstant sind. Ist n eine Richtung senkrecht zur Licht­fort­pflanzung, so ergibt das Huygenssche Prinzip, dass der Licht­strahl [in der Ebene (γ, n) betrachtet] die Krümmung −dγ/∂n besitzt.

Abb. 1: Zeigt die von Einstein skizzierte Abweichung eines Lichtstrahls

Nun gilt es, die Krümmung zu unter­suchen, welche ein Licht­strahl voll­zieht, der im Abstand n an einer Masse M vorbei­geht. Wählt man das Koordi­naten­system gemäß der vor­stehenden Skizze, so ist die gesamte Biegung B des Licht­strahls (positiv gerechnet, wenn sie nach dem Ursprung hin konkav ist) in genügender Näherung gegeben durch:

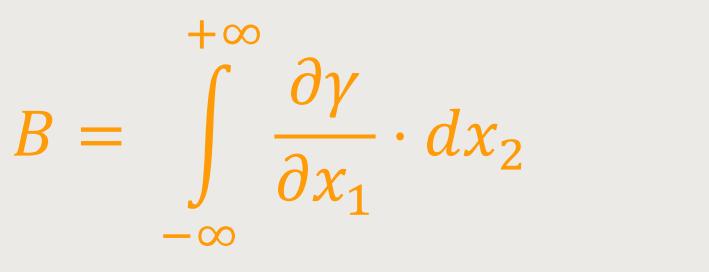
Während (73) und (70) folgendes ergeben:

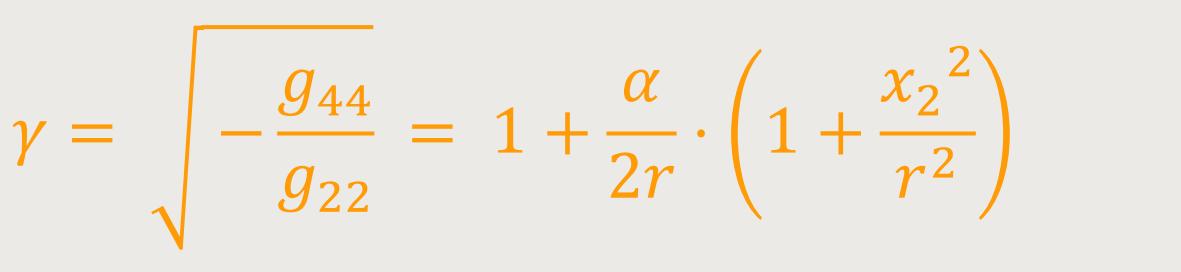
Als Ergebnis erhält man: (74)

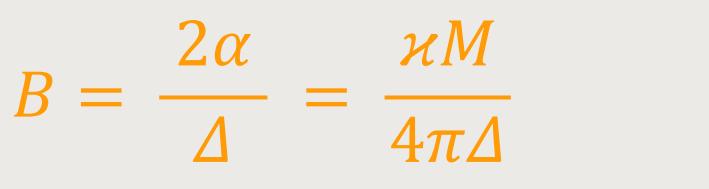
Laut Einsteins Berechnungen voll­zieht ein an der Sonne vorbei­gehender Licht­strahl demnach eine Biegung von 1,7'', wogegen ein am Planten Jupiter vorbei­gehender Strahl eine Biegung von 0,02'' vollzieht.

Berechnet man das Gravitations­feld um eine Größen­ordnung genauer, und ebenso mit entspre­chender Genauig­keit die Bahn­bewegung eines materiellen Punktes von relativ unendlich kleiner Masse, so erhält man gegen­über den Kepler-Newton­schen-Gesetzen der Planeten­bewegung eine Abweichung von folgender Art. Die Bahn­ellipse eines Planeten erfährt in Richtung der Bahn­bewegung pro Umlauf eine langsame Drehung mit folgendem Wert: (75)

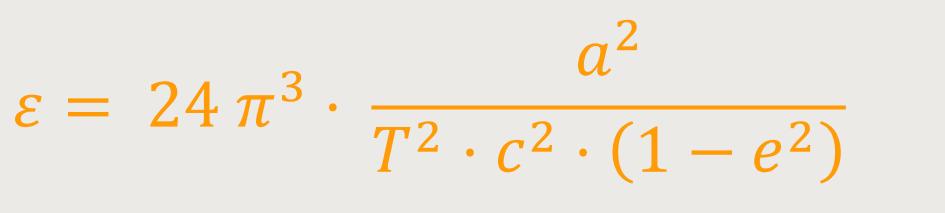
In dieser Formel bedeutet a die große Halbachse, c die Licht­geschwin­dig­keit in üblichem Maße, e die Exzentri­zität, T die Umlaufzeit in Sekunden.

Die Berechnung ergibt für den Planeten Merkur eine Drehung der Bahn um 43'' pro Jahrhundert, genau entspre­chend der Konstatierung des Astronomen Le Verrier. Dieser fand nämlich einen durch Störungen der übrigen Planeten nicht erklärbaren Rest der Perihel­bewegung dieses Planeten von der angegeben Größe.

⇦ Kapitel Kapitel ⇨