Nun erhebt sich die Frage, welche Umstände uns eine veränderte Sicht von Raum und Zeit aufzwingen? Denn wenn die neue Sicht­weise den Natur­erschei­nungen nicht wider­spricht, eröffnet sich die Möglich­keit, Beziehungen ein­deutig zu definieren. Bevor Minkowski darauf einging, stellte er eine wichtige Bemerkung voran.

Wenn Raum und Zeit eine Erwei­terung erfahren haben, so ent­spricht einem ruhenden substan­ziellen Punkt als Welt­linie eine zur t-Achse parallele Gerade. Handelt es sich dagegen um einen gleich­förmig bewegten substan­ziellen Punkt, so ist es eine gegen die t-Achse geneigte Gerade. Und wenn es schließ­lich um einen ungleich­förmig bewegten substan­ziellen Punkt geht, ist die Welt­linie irgendwie gekrümmt.

Setzen wir einen beliebigen „Welt­punkt” x, y, z, t nun der jeweiligen Welt­linie gleich, und verläuft diese in der oben beschrie­benen hyper­boloidischen Schale parallel zu irgend­einem Radius­vektor OA', so kann die Strecke OA' dann als neue Zeit­achse einge­führt werden. Und aus­gehend von dem neu definierten Verständnis von Raum und Zeit erscheint die Substanz in dem betref­fenden Welt­punkt als ruhend.

Hierzu führte Minkowski folgendes Axiom ein:
Die in einem beliebigen Welt­punkt vorhandene Substanz kann stets bei geeigneter Fest­setzung von Raum und Zeit als ruhend auf­gefasst werden.

Das Axiom besagt, dass in jedem Welt­punkt stets der Ausdruck

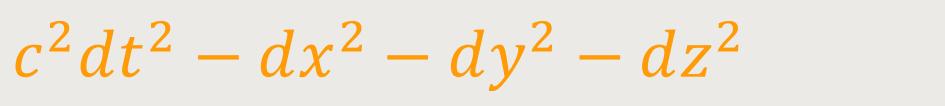
... Gültig­keit hat. Oder mit anderen Worten, jede Geschwin­dig­keit v ist stets kleiner als die Licht­geschwin­dig­keit c. Bezogen auf alle substan­ziellen Geschwin­dig­keiten würde c als obere Grenze bestehen und hierin die tiefe Bedeutung der Größe c liegen.

Nach Minkowski scheint dieses Axiom auf den ersten Blick etwas Unbefriedi­gendes zu beinhalten. Er gibt zu bedenken, dass eine modifizierte Mechanik vonnöten ist, was bedeutet, dass in obiger Differen­tial­gleichung zweiten Grades die Quadrat­wurzel mit eingeht. Dies sei notwendig, damit auch Fälle von Über­licht­geschwindig­keit eine Rolle spielen können, so wie es auch in der Geometrie „Figuren” mit imaginären Koordinaten gibt.

Ausschlag­gebend für die Annahme, dass sich die Gruppe G_c so verhält, kommt daher, weil die Differen­tial­gleichung diesen Aspekt der Ausbreitung von Licht­wellen im leeren Raum beinhaltet. Anderer­seits macht der Begriff „starrer Körper” nur in einer Mechanik mit der Gruppe G_∞ einen Sinn.

Minkowski schluss­folgerte, dass wenn man beispiels­weise die Gruppe G_c betrachtet und es gäbe es starre Körper, man erkennen könnte, dass durch die zwei zu den beiden Gruppen G_c und G_∞ gehörenden hyper­boloidischen Schalen nur „eine” t-Richtung verläuft. Und das würde als Konsequenz bedeuten, dass man an geeig­neten starren optischen Instrumenten eine Verän­derung der Erscheinungen bei unter­schied­licher Ausrichtung gegen die Rotations­richtung der Erde wahr­nehmen müsste.

Alle Bemühungen in diese Richtung, insbe­sondere der Versuch von Michelson, zeigten jedoch ein negatives Ergebnis. Um eine Erklä­rung dafür zu finden, ent­wickelte H.A. Lorentz eine Hypothese, deren Erfolg in der Invarianz (Unver­änder­lich­keit) der Betrach­tung für die Gruppe G_c zu finden ist. Nach Lorentz soll jeder Körper, der in Bewegung ist, in Richtung der Bewegung eine Verkür­zung erfahren, und zwar bei einer Geschwin­dig­keit v im Verhältnis

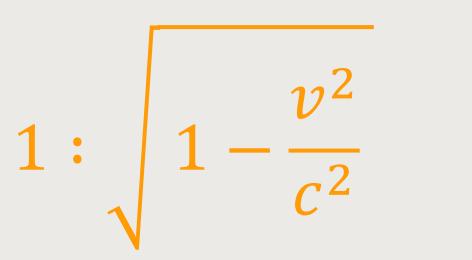
Diese Hypothese klang für Minkowski äußerst phantastisch. Denn die Kontraktion sei nicht eine Folge von Wider­ständen im Äther, so wie man sich das All ursprünglich vorstellte, sondern ein Glücks­fall, quasi als Begleit­umstand der Bewegung zu sehen.

Minkowski wollte nun an einer Grafik veranschau­lichen, dass die Hypothese von Lorentz völlig äquivalent mit Einsteins Aufsatz über die Auffassung von Raum und Zeit ist, wodurch sie viel verständ­licher wird.

Der Einfach­heit halber trennen wir die Dimen­sionen y und z gedank­lich ab, und denken uns nur mehr eine räum­lich 1-dimensionale Welt. Daraus ergibt sich ein entsprechend der t-Achse aufrechter und ein gegen die t-Achse geneigter Parallel­streifen (siehe Abb. 1). Die Dar­stellung spiegelt den Verlauf eines ruhenden, bezüg­lich eines gleich­förmig bewegten Körpers wider, der jedes Mal eine konstante räum­liche Ausdehnung behält.

Abb. 1: Zeigt in der rechten Hälfte die von Minkowski skizzierten Parallelstreifen

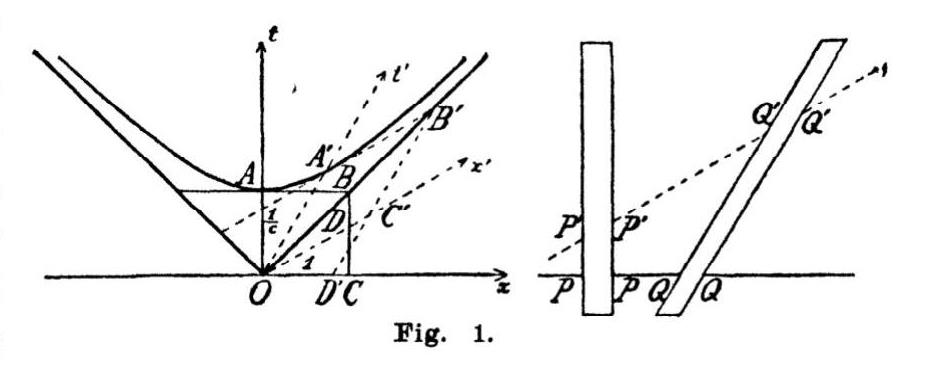
Ist der Abschnitt OA' parallel zum zweiten Streifen, so können wir t' als Zeit und x' als Raum­koordinate ein­führen. Und es erscheint dann der zweite Körper als ruhend, der erste dagegen als gleich­förmig bewegt. Des Weiteren nehmen wir an, dass der erste Körper im Ruhe­zustand die Länge l hat, d.h. der Quer­schnitt PP des ersten Streifens auf der x-Achse dem Wert l · OC ent­spricht, wobei OC die Einheits­größe auf der x-Achse repräsen­tiert. Anderer­seits hat der zweite Körper, als ruhend auf­gefasst, die gleiche Länge l. Letzteres bedeutet dann, dass der parallel zur x'-Achse gemessene Quer­schnitt des zweiten Streifens, sprich Q' Q' dem Wert l · OC' entspricht.

Durch diese zwei Körper werden zwei gleiche Lorentzsche Elek­tronen abgebildet, ein ruhendes und ein gleich­förmig bewegtes. Hält man aber an den ursprüng­lichen Koordinaten x, t fest, so ist als Aus­dehnung des zweiten Elektrons der Quer­schnitt Q Q seines zuge­hörigen Streifens parallel der x-Achse anzugeben. Daraus wird deutlich, dass Q' Q' = l · OC' und Q Q = l · OD' ent­spricht. Eine Rechnung ergibt, dass wenn dx/dt für den zweiten Streifen = v steht, sowie OQ' = OC · √(1 - (v²/c²)), demnach auch PP : QQ = 1 : √(1 - (v²/c²)) ent­spricht.

Und genau das sei der Sinn der Lorentzschen Hypothese, bezüg­lich der Kontraktion der Elektronen bei Bewegung. Fassen wir anderer­seits das zweite Elektron als ruhend auf, über­nehmen also das Bezugs­system x', t', so ist als Länge des ersten Elektrons mit dem Quer­schnitt P' P' seines Streifens parallel OQ' zu bezeichnen. Und man würde in genau dem bezeich­neten Verhältnis das erste Elektron gegen­über dem zweiten Elektron verkürzt wahrnehmen.

Entspre­chend obiger Abbildung erhält folgende Beziehung:

Lorentz bezeichnete in seiner Abhand­lung die Verbindung t' von x und t als Orts­zeit des gleich­förmig bewegten Elektrons und benutze eine physika­lische Konstruktion dieses Begriffs zum besseren Verständnis der Kontraktions­hypothese. Jedoch zu erkennen, dass die Zeit des einen betrachteten Elektrons dem des anderen gleicht, also t und t' gleich­zusetzen ist, sei erst ein Verdienst von A. Einstein gewesen.

Damit war der Begriff „Zeit” durch die Darstellungen als eine ein­deutige Größe fest­gelegt worden. An dem Begriff des „Raums” rüttelten weder Einstein noch Lorentz viel­leicht auch deshalb nicht, weil bei der oben ange­führten Trans­forma­tion, bei der die x', t'-Ebene sich mit der x, t-Ebene deckt. Was die Schluss­folgerung zulässt, als sei die x-Achse des Raums in ihrer Lage erhalten geblieben. Über den Begriff des „Raums” in entspre­chender Weise hinweg­zuschreiten, sei wohl nur als Verwegen­heit der mathe­matischen Kultur einzu­ordnen.

Nach dem nun zwingend not­wendigen erlangten Verständnis der Gruppe G_c erschien Minkowski das Wort „Relativitäts­postulat” für die Forderung einer Unveränder­lich­keit der Gruppe G_c nicht aus­reichend. Das würde dem Sinn nach bedeuten, dass durch die Erschei­nungen in Raum und Zeit nur eine 4-dimen­sionale Welt abge­bildet wird, aber die Projek­tion in Raum und in Zeit für sich noch mit einer gewissen Freiheit vor­genommen werden kann. Aus diesem Grund verwendete Minkowski lieber den Namen „Postulat der absoluten Welt” (oder kurz Weltpostulat).

Durch das neu definierte Welt­postulat wird es nach Minkowskis Ansicht möglich, die vier Bestimmungs­stücke x, y, z, t gleich zu behandeln.

Vor allem wird deutlich, was es mit dem Begriff Beschleu­nigung auf sich hat.

Minkowski bediente sich hierzu einer geome­trischen Ausdrucks­weise, die sich nach seinen Worten anbietet, wenn man im Tripel, also dort, wo die Koordinaten­punkte x, y, z zusammen­treffen, still­schweigend nur noch von dem Punkt z spricht. In diesen Punkt wird nun der Raum-Zeit-Null­punkt O gelegt.

Der Kegel, definiert als

... und mit dem Punkt O als dessen Spitze (siehe Abb. 2), besteht aus zwei Teil­bereichen. Der eine Bereich mit den Werten Null­punkt t < 0, und der andere Bereich mit den Werten t > 0.

Abb. 2: Zeigt die von Minkowski skizzierten zwei Bereiche

Den ersten, uns zuge­wandten Bereich, hatte Minkowski als „Vor­kegel” bezeichnet, der aus allen Welt­punkten bestehen soll, die Licht „in Richtung O senden”. Der zweite, von uns weg­gewandte Bereich, bezeich­nete er als „Nach­kegel”, der seiner­seits aus allen Welt­punkten besteht, die Licht „von O aus­gehend” empfangen. Die vom Vor­kegel einge­grenzte Fläche bezeich­nete Minkowski als „dies­seits von O” und die Fläche des Nach­kegels als „jenseits von O”. Jenseits von O entspräche dann der weiter oben betrach­teten hyper­boloidischen Schale:

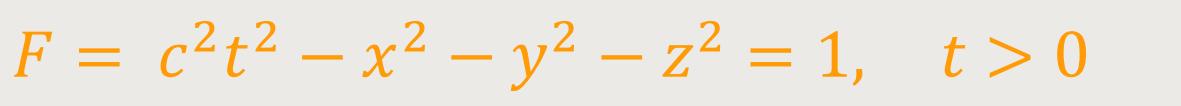
Der Bereich zwischen den Kegeln wird ein­gegrenzt von den ein­schaligen hyper­boloidischen Verläufen

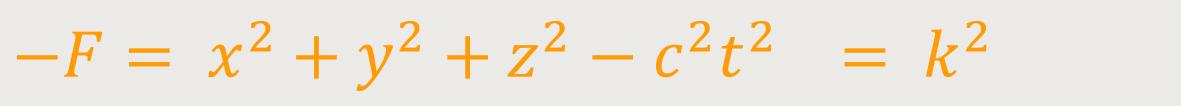
... und beinhaltet alle konstanten positiven Werte k². Für uns sind besonders die Hyperbeln wichtig, die den Punkt O als deren Mittelpunkt haben und obiger Darstellungen seitlich liegen.

Die einzelnen Äste dieser Hyperbeln werden zunächst als „Zwischen­hyperbeln zum Zentrum” O bezeichnet. Ein derartiger Hyperbelast würde, wenn er einer Welt­linie eines substan­ziellen Punktes entspräche, eine Bewegung wider­spiegeln, die für t = −∞ und t = +∞ sich asymptotisch der Licht­geschwin­dig­keit c annähert.

In Anlehnung an den klassischen Vektor­begriff in einem Raum soll jetzt eine definierte Strecke stell­vertretend für alle Möglich­keiten x, y, z, t als Vektor bezeichnet werden. Dabei wird aller­dings unter­schieden zwischen den zeit­artigen Vektoren, die vom Punkt O wegzeigen. Diese Vektoren zeigen in Richtung der Schale +F = 1, t > 0, und stehen für die Zeit. Die raum­artigen Vektoren zeigen in Richtung des Bereichs mit −F = 1, und stehen für den Raum. Die Zeit­achse an sich kann mit jedem Zeit­vektor parallel verlaufen. Jeder Welt­punkt, der zwischen dem Vor­kegel und dem Nach­kegel liegt, kann auf Grund­lage des Bezugs­systems ent­weder mit dem O-Punkt zusammen­fallen, oder früher als O bzw. später als O posi­tioniert werden. Damit ist dann ein­deutig definiert, ob sich ein Welt­punkt zeitlich vor oder nach dem O-Punkt befindet. Beim Grenz­über­gang c = ∞ würde es in diesem Fall zu einem voll­ständigen Zusammen­klappen des keil­förmigen Ein­schnitts zwischen den Kegeln kommen, was der „ebenen” Mannig­faltig­keit t = 0 ent­spricht. In der Grafik wurden die Bereiche absicht­lich unter­schied­lich breit dargestellt.

Einen solch beliebigen Vektor x, y, z, t, der von O ausgeht, zerlegen wir nun in seine vier Komponenten x, y, z, t. Treffen die Richtungen zweier Vektoren bzw. die eines Radiusvektors mit den Punkten OR vom Punkt O ausgehend, mit einer der Flächen ± F = 1 zusammen, und ergibt sich eine Tangente mit den Punkten RS im Punkt R der betref­fenden Fläche, so sollen die Vektoren mit „normal” zueinander bezeichnet werden. Dement­spre­chend gilt:

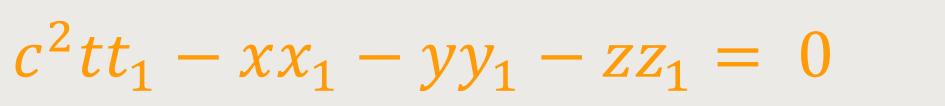
Diese Bedingung legt fest, dass die Vektoren mit den Kompo­nenten x, y, z, t und x₁, y₁, z₁, t₁ normal zueinander stehen.

Für die Beträge der Vektoren der unter­schied­lichen Richtungen sollen Einheits­größen fest­gelegt werden. Insofern soll einem raum­artigen Vektor vom Punkt O aus­gehend, hin zum Bereich −F = 1, stets der Betrag 1 zugewiesen werden. Wogegen für einen zeit­artigen Vektor, eben­falls aus­gehend vom Punkt O hin zum Bereich +F = 1, t > 0 stets der Betrag 1/c gelten soll.

Versetzten wir uns nun gedank­lich in einen solchen Welt­punkt P der durch seine Kompo­nenten x, y, z, t bestimmt ist, und die durch einen substan­ziellen Punkt verlaufende Welt­linie. Verfolgt man diesen Punkt auf seinem Weg, ergibt sich für den Betrag des zeit­artigen Vektor­elements dx, dy, dz, dt im weiteren Verlauf der Linie der Betrag:

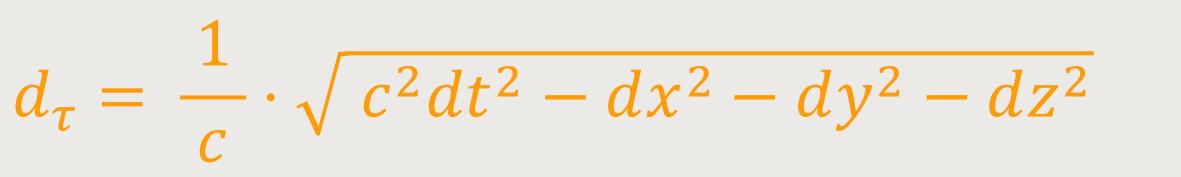
Das Integral ∫ d_τ = τ dieses Betrags auf der Welt­linie, aus­gehend von einem festen Ausgangs­punkt P₀ bis zu dem variablen Endpunkt P, soll als die „Eigen­zeit” des substan­ziellen Punktes im jewei­ligen Punkt P bezeichnet werden.

Auf der Welt­linie sollen die Kompo­nenten 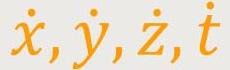x, y, z, t, die dem Vektor OP entspre­chen, als Funktionen der Eigen­zeit τ betrachtet werden. Der erste Differential­quotient nach τ wird mit bezeichnet. Der zweite Differen­tial­quotient nach τ wird mi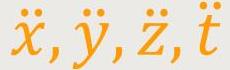t bezeichnet. Die dazu­gehörigen Ableitungen des Vektors OP nach τ bezeichnen wir als „Bewegungs­vektor” im Punkt P, und die Ableitung dieses Bewegungs­vektors nach τ bezeichnen wir als „Beschleu­nigungs­vektor” im Punkt P. In diesem Fall gilt:

Das heißt, der Bewegungs­vektor ist der zeit­artige Vektor in Richtung der Welt­linie im Punkt P mit dem Betrag 1, und der Beschleu­nigungs­vektor im Punkt P ist normal zum Bewe­gungs­vektor in diesem Punkt P, in jedem Fall ein raum­artiger Vektor.

Bei näherer Betrachtung gibt es einen Hyperbelast, der mit der Welt­linie im Punkt P drei unend­lich benach­barte Punkte hat. Und das dies die vom Vor­kegel und Nach­kegel erzeugten Asymptoten sind (siehe Abb. 3, nächstes Kap.). Diesen Hyperbelast bezeichnen wir fortan mit „Krümmungs­hyperbel” im Punkt P. Ent­spricht der End­punkt M dem Zentrum dieser Hyperbel, so handelt es sich hierbei um eine Zwischen­hyperbel aus­gehend vom Zentrum M. Als Betrag des Vektors MP wählen wir ϱ, wobei man den Beschleu­nigungs­vektor im Punkt P als den Vektor in Richtung MP mit dem Betrag c²/ϱ auf­fassen kann.

Sind die Kompo­nenten 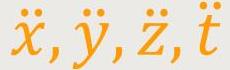alle­samt Null, so reduziert sich die Krümmungs­hyperbel auf die im Punkt P die Welt­linie berüh­rende Gerade, worauf­hin für ϱ = ∞ gilt.

⇦ Kapitel Kapitel ⇨