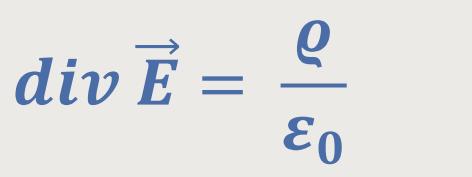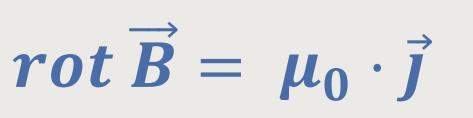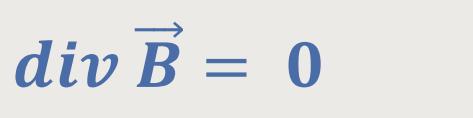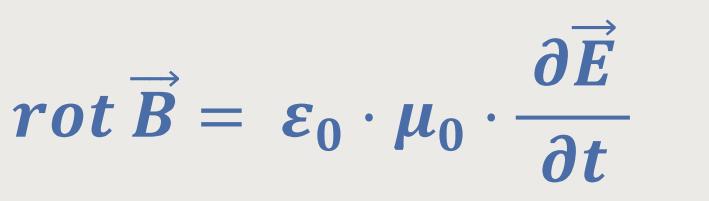Die vier Maxwell-Gleichungen inklusive der Lorentzkraft bilden die Grundlage für die Feldtheorie der Elektrodynamik. Diese Gleichungen beinhalten gewisse symmetrische und unsymmetrische Strukturen. Um das zu verdeutlichen, bedient man sich geometrischer Überlegungen.
Deshalb werden wir nun betrachten, in welcher Weise sich aus vorhandenen Ladungen und Strömen elektrische und magnetische Felder ergeben.
Als erstes betrachten wir die statischen Felder.
Grafik (wird später eingefügt)
Hierzu kann man sich gedanklich eine Punktladung q
vorstellen, um die herum sich ein elektrisches Feld befindet. Die Feldlinien und die
Feldstärkevektoren  sind
alle strahlenförmig angeordnet. Positive Ladungen zeigen nach außen, negative
Ladungen zeigen nach innen.
sind
alle strahlenförmig angeordnet. Positive Ladungen zeigen nach außen, negative
Ladungen zeigen nach innen.
Die 1. Maxwell-Gleichung beschreibt diesen Prozess:
Bei dieser Beziehung spielt die Ladungsdichte eine Rolle. Es ist aber auch möglich, ein statisches Feld aufgrund einer Stromdichte zu erzielen.
Grafik (wird später eingefügt)
In diesem Fall wird der Strom I durch die Stromdichtevektoren
 beschrieben, der sich mit einem
magnetischen Feldwirbel
beschrieben, der sich mit einem
magnetischen Feldwirbel  umgibt. Die Rotation dieses Vektorfeldes
umgibt. Die Rotation dieses Vektorfeldes 
Die 2. Maxwell-Gleichung beschreibt diesen Prozess:
Diese Beziehung beinhaltet nicht den elektrischen Verschiebungsstrom, weil es jetzt nur um statische Felder geht.
Im Gegensatz dazu gibt es zeitabhängige magnetische Felder, die in der Realität eher die Regel sind.
Grafik (wird später eingefügt)
In diesem Fall wird das magnetische Feld durch die Feldvektoren
 beschrieben. Da sich diese Vektoren
zeitlich ändern, lassen sie sich beschreiben als:
beschrieben. Da sich diese Vektoren
zeitlich ändern, lassen sie sich beschreiben als:
 / ∂t
/ ∂t
Diese Vektoren sind den Feldvektoren entgegengerichtet, was zu einem kleineren magnetischen Feld führt.
Und die 3. Maxwell-Gleichung, die das beschreibt, lautet:
Somit ist der Rotationsvektor

 / ∂t
/ ∂t
Insofern umgibt sich ein zeitlich änderndes magnetisches Feld mit einem elektrischen Wirbelfeld. Und genau das erhält man aus dem Induktionsgesetz. Denn die Induktionsspannung ist ein Anzeichen dafür, dass es ein elektrisches Wirbelfeld geben muss.
Darüber hinaus gibt es noch zeitlich veränderliche elektrische Felder.
Grafik (wird später eingefügt)
In diesem Fall wird ein zeitlich veränderliches elektrisches Feld durch die
Feldvektoren  beschrieben. Hierzu
kann man sich gedanklich zwei Kondensatorplatten vorstellen, zwischen denen ein
solches Feld liegt. Und wenn sich der Kondensator auflädt, umgibt sich dieses
elektrische Feld mit einem magnetischen Feldwirbel
beschrieben. Hierzu
kann man sich gedanklich zwei Kondensatorplatten vorstellen, zwischen denen ein
solches Feld liegt. Und wenn sich der Kondensator auflädt, umgibt sich dieses
elektrische Feld mit einem magnetischen Feldwirbel
 . Und wenn sich das elektrische Feld
durch den Ladestrom verändert, ergibt sich ein elektrischer
Feldstärkevektor
. Und wenn sich das elektrische Feld
durch den Ladestrom verändert, ergibt sich ein elektrischer
Feldstärkevektor
 / ∂t
/ ∂t
Die 4. Maxwell-Gleichung, die das beschreibt, lautet:
Hier wurde der zusätzliche Term

An dieser Stelle ist noch zu erwähnen, dass sich verschiedene Felder durchaus überlagern können. Und da die Maxwell-Gleichungen lineare Differentialgleichungen sind, ist auch das „Superpositionsprinzip” gültig. Mit anderen Worten, es werden sich die Felder, wenn sie von unterschiedlichen Quellen herrühren, auch linear überlagern. Das gilt aber nur für moderate Feldstärken. Denn bei hohen Feldstärken kommt es zu nichtlinearen Phänomenen.
Bisher haben wir nur langsame Veränderungen betrachtet. In den meisten Fällen bildet sich aber ein elektrisches oder magnetisches Feld „schlagartig” und unmittelbar aus. Bei besonders hohen Frequenzen kommt es zu zeitlichen Verzögerungen der voneinander in Abhängigkeit stehenden Felder. So dass es dann schließlich zu einer Wellenausbreitung kommt.
Bevor wir uns aber der Wellenausbreitung zuwenden, werden wir die elektromagnetischen
Schwingungen betrachten. Hierbei geht es noch um Frequenzen, die langsam genug ist. In der
Wechselstromlehre haben wir typischer Weise Frequenzen bis
Nachdem wir nochmals alle Maxwell-Gleichungen gegenübergestellt haben, wenden wir uns jetzt den magnetischen Eigenschaften der Materie zu.
Bei den magnetischen Eigenschaften zeigt sich, dass im Allgemeinen die Beeinflussung eines Magnetfeldes durch die Anwesenheit einer magnetisierbaren Materie sehr gering ist. Anders verhält es sich dagegen bei dem Ferromagnetismus.
Dort lassen sich ganz besondere Effekte beobachten, die um einen Faktor 1.000 oder sogar 10.000 höher ausfallen. Diesen ferromagnetischen Medien haben wir eine Vielzahl heutiger Technologien zu verdanken.
Doch wenn man über magnetische Eigenschaften spricht, betrachtet man zuerst die magnetischen Dipole. in einem früheren Kapitel wurde bereits das magnetische Dipolmoment behandelt.
Grafik (wird später eingefügt)
Es ging um eine stromdurchflossene Stromschleife, die eine kreisförmige
Fläche umschließt. Diese Fläche hat einen Flächenvektor
 , der senkrecht auf der Fläche steht.
Der Strom I fließt nach der Rechte-Hand-Regel rechts herum. Das
magnetische Dipolmoment
, der senkrecht auf der Fläche steht.
Der Strom I fließt nach der Rechte-Hand-Regel rechts herum. Das
magnetische Dipolmoment
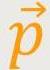 m
m
Das magnetische Dipolmoment war definiert als:
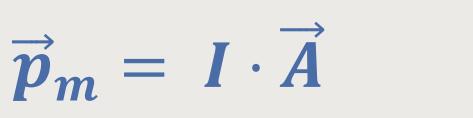
Somit besteht ein Unterschied zwischen dem magnetischen und dem elektrischen Dipol.
Grafik (wird später eingefügt)
Denn beim elektrischen Dipol war es so, dass es zwei gleich große,
gegensätzliche Punktladungen gibt, die mit einem Verbindungsvektor
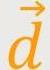 verbunden sind. Dieser Vektor zeigt von
der negativen zur positiven Ladung. Das elektrische Dipolmoment
verbunden sind. Dieser Vektor zeigt von
der negativen zur positiven Ladung. Das elektrische Dipolmoment
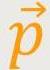 e
e
Und das elektrische Dipolmoment war definiert als:
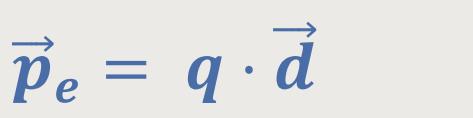
Ein magnetischer Dipol wird aber nicht wie beim elektrischen Dipol durch zwei Punktpole realisiert, sondern vielmehr durch einen Kreisstrom, der eine Fläche umschließt. Jetzt stellt sich natürlich die Frage, wie die Felder im Detail ausschauen.
Beim elektrischen Dipol ist es sehr einfach, denn die Feldlinien zeigen immer in einem Bogen von +q nach −q. Bei der Stromschleife dagegen umschließen die Feldlinien den dünnen stromdurchflossenen Leiter. Was ergibt sich daraus?
Im Fernfeld, also wenn man relativ weit weg ist von den Dipolen, haben beide Felder eine gewisse Ähnlichkeit. Schaut man sich dagegen das Nahfeld im Innern dieses Dipols an, zeigt das magnetische Feld in Richtung des magnetischen Dipolmoments, wogegen das elektrische Feld genau in entgegengesetzte Richtung zum elektrischen Dipolmoment zeigt. Und das ist der Grund dafür, warum die magnetischen Werkstoffe das Feld beim magnetischen Dipol noch verstärken, wogegen das Feld beim elektrischen Dipol abgeschwächt wird.
Wir erinnern uns, beim Berechnen eines Magnetfeldes einer kreisförmig
stromdurchflossenen Leiterschleife hatte sich ergeben, dass bei zunehmendem
Abstand von der Schleife, die magnetische Flussdichte betragsmäßig mit
Die Moleküle, die einen derartigen magnetischen Dipol aufweisen, werden sich in einem äußeren magnetischen Feld ebenfalls ausrichten können. Diese Ausrichtung führt letztlich dazu, dass das Magnetikum spezielle Eigenschaften aufweist.
Wir betrachten zunächst, wie sich ein magnetischer Dipol in einem homogenen äußeren magnetischen Feld verhält. Wieder geht es zunächst einmal um eine stromdurchflossene Schleife, bei der sich zusätzlich ein äußeres Magnetfeld ausbildet. Insofern ergeben sich Ströme in diesem äußeren Magnetfeld, die durch die Lorentzkraft hervorgerufen werden.
 (a)
(a)
Für die weitere Überlegung kann man sich eine rechteckige Stromschleife vorstellen, die sich in einem solchen äußeren Magnetfeld befindet.
Grafik (wird später eingefügt)
Hierzu denkt man sich ein horizontal verlaufendes äußeres Magnetfeld
 (a),
welches z.B. von links nach rechts verläuft. Dieses Magnetfeld tritt durch die besagte
rechteckige Fläche hindurch, die in diesem Fall allerdings nicht senkrecht
zum Feld steht, sondern schräg angeordnet ist. Sodass der Flächenvektor
(a),
welches z.B. von links nach rechts verläuft. Dieses Magnetfeld tritt durch die besagte
rechteckige Fläche hindurch, die in diesem Fall allerdings nicht senkrecht
zum Feld steht, sondern schräg angeordnet ist. Sodass der Flächenvektor
 , der ja immer senkrecht zur Fläche
steht, jetzt ebenfalls in einem Winkel zum Magnetfeld steht.
, der ja immer senkrecht zur Fläche
steht, jetzt ebenfalls in einem Winkel zum Magnetfeld steht.
Die Eckpunkte des Rechtecks werden im Uhrzeigersinn mit 1,
2, 3 und 4 bezeichnet,
beginnend mit 1 unten rechts. Dementsprechend soll der Strom
in dieser rechteckigen Stromschleife rechtsläufig fließen. Nun kann
man die Lage der Stromschleife noch mit zwei Einheitsvektoren beschreiben. Am
Eckpunkt 1 verläuft der eine Einheitsvektor
 a
a b
b m
m
Nun möchte man wissen, welche Kraft auf eine solche Fläche in einem homogenen äußeren Magnetfeld ausgeübt wird. Hierzu rechnet man sich die Lorentzkraft für alle vier Teilabschnitte aus.
Wir erinnern uns, diese Lorentzkraft wurde definiert als:
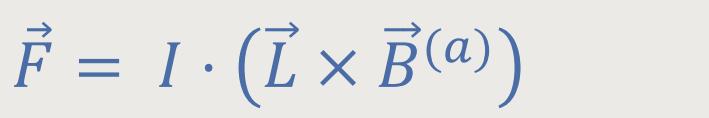
 ist ein Teilabschnitt der
Leiterschleife
ist ein Teilabschnitt der
Leiterschleife
Die Kräfte auf die beiden Leiterabschnitt b sind entgegengesetzt gerichtet und in der gleichen Wirkungslinie. Daher kompensieren sich diese beiden Kräfte. Anders verhält es sich dagegen mit den Teilabschnitten a. Die Kräfte auf die Teilabschnitte a sind zwar auch gleich groß und entgegengesetzt, liegen aber aufgrund der Verdrehung nicht auf der gleichen Wirkungslinie und bilden deshalb ein Kräftepaar. Aus der Statik wissen wir, dass ein solches Kräftepaar ein Drehmoment bewirkt. Deshalb schauen wir uns die Kräfte auf die Leiterstücke a genauer an.
Die Kraft für den Teilabschnitt
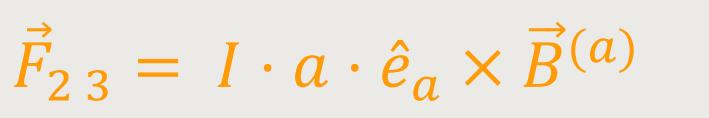
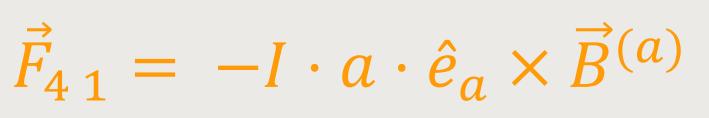
 "Dach"
ist immer ein Vektor mit der Länge Eins
"Dach"
ist immer ein Vektor mit der Länge Eins
Da die beiden Kräfte entgegengesetzt nach außen gerichtet sind, wird sich die Fläche der Leiterschleife so ausrichten wollen, das der Flächenvektor mit dem magnetischen Feld parallel ausgerichtet ist.
Grafik (wird später eingefügt)
Der Ausdruck für das Drehmoment lautet entsprechend:
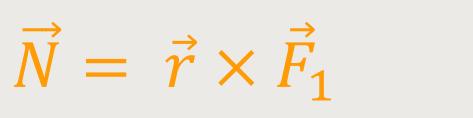
Durch Einsetzten erhält man ein doppeltes Vektorprodukt:
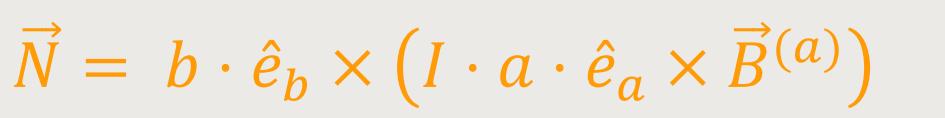
Wenn man alle konstanten skalaren Faktoren heraushebt, ergibt sich nach Umformung:
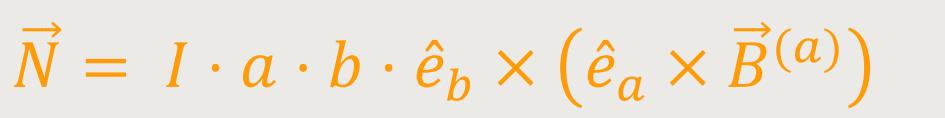
Eine Vektorproduktregel lautet:
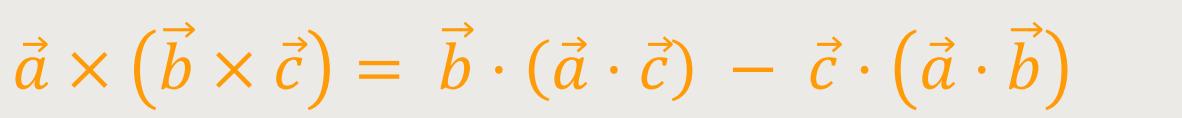
Und wenn man diese Regel umformt, erhält man:
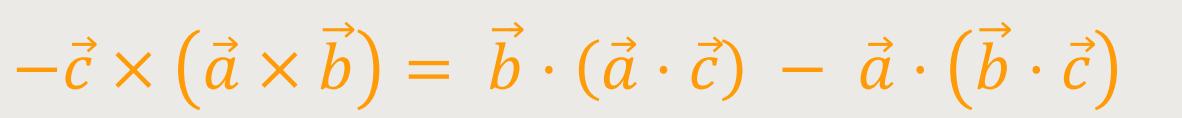
In diesem Fall kann man für das linke Vektorprodukt auch schreiben:

Bei obiger Produktregel sagt der zweite Term aus, falls bei der Stromschleife ...

... vorliegt, die Stellung der Klammern geändert werden darf, sodass daraus folgt:
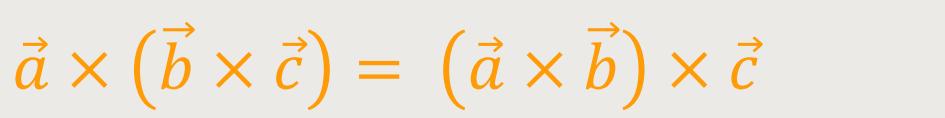
Und genau das wird bei obigem Drehmoment ausgesagt.
Da beide senkrecht zueinander stehen, darf die Lage der Klammern bei dem doppelten Vektorprodukt verändert werden. Insofern ergibt sich jetzt durch Umformung:
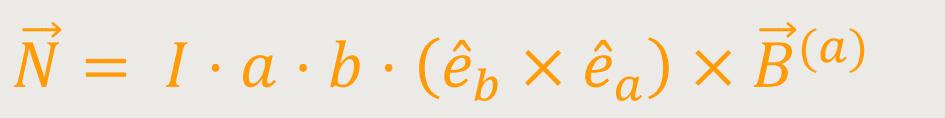
Dieses  b ×
b ×
 a )
a ) .
.
Und I ·
 entspricht dem magnetischen
Dipolmoment
entspricht dem magnetischen
Dipolmoment
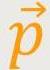 m
m
Damit ergibt sich für das Drehmoment die einfache Beziehung:
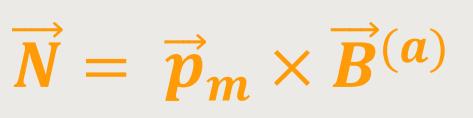
Und wir erinnern uns, für das elektrische Dipolmoment galt analog:
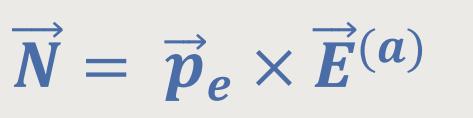
Insofern erkennt man auch hier eine gewisse Symmetrie.
Was wird aber letztlich durch die Definition des Drehmoments ausgesagt?
Das Kräftepaar wird so lange wirken, bis das magnetische Dipolmoment
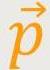 m
und das äußere Magnetfeld
m
und das äußere Magnetfeld
 (a)
parallel zueinander ausgerichtet sind. Denn das vektorielle Produkt zweier paralleler
Vektoren ist Null. Das Drehmoment des äußeren Feldes
bewirkt, dass sich die stromdurchflossene Schleife zum äußeren
Magnetfeld quer stellt. Und in diesem Fall zeigt auch das eigene Magnetfeld der
Stromschleife in die gleiche Richtung wie das äußere Magnetfeld. Durch die
gleiche Ausrichtung der beiden magnetischen Felder wird das äußere Magnetfeld
sogar noch verstärkt.
(a)
parallel zueinander ausgerichtet sind. Denn das vektorielle Produkt zweier paralleler
Vektoren ist Null. Das Drehmoment des äußeren Feldes
bewirkt, dass sich die stromdurchflossene Schleife zum äußeren
Magnetfeld quer stellt. Und in diesem Fall zeigt auch das eigene Magnetfeld der
Stromschleife in die gleiche Richtung wie das äußere Magnetfeld. Durch die
gleiche Ausrichtung der beiden magnetischen Felder wird das äußere Magnetfeld
sogar noch verstärkt.
Damit erhält man folgende Aussage:
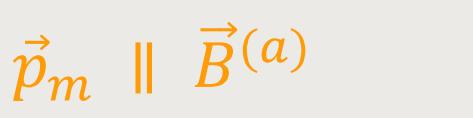
Wir haben also eine Gleichorientierung, die zu einer Verstärkung des äußeren Magnetfeldes führt.
Dagegen ist es beim elektrischen Feld genau anders herum. Der elektrische Dipol richtet sich so aus, dass sein eigenes inneres Feld entgegengerichtet ist gegen das äußere elektrische Feld, und dieses damit abgeschwächt wird.
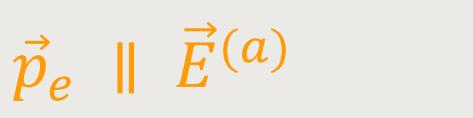
Wir haben auch hier eine Gleichorientierung, die aber wie erwähnt, zu einer Abschwächung des äußeren elektrischen Feldes führt.
Und auf diesen Unterschied kommt es letztlich an, denn der Ferromagnetismus zeichnet sich durch die Verstärkung des äußeren Magnetfeldes aus.
⇦ Kapitel Kapitel ⇨