Bei diesem Experiment geht es um die Bewegung von einzelnen Ladungs­trägern in einem Gas. Auf ihrem Weg durch das verdünnte Gas werden die Gasmole­küle durch Stoß angeregt, und fallen anschließend wieder in ihren Grund­zustand zurück. Das Ganze findet unter Emission von Photonen statt. Diese Photonen kann man als eine Licht­erscheinung sehen, sodass eine Lichtspur der geladenen Teilchen zu erkennen ist.

Grafik (wird später eingefügt)

Hierzu betrachtet man einen kugel­förmigen Glasbe­hälter, in dessen Innen­raum an einer außer­mittigen Stelle eine Elektronen­kanone angebracht ist. Auf diese Weise werden durch eine Glüh­wendel Elektronen emittiert. Zusätzlich wird im Innern eine Beschleu­nigungs­spannung angelegt, bei der die Elektronen auf eine gewisse Energie beschleunigt werden. Dement­sprechend tritt zunächst ein gerad­liniger Elektronen­strahl aus.

Auf den Glasbe­hälter wirkt nun von außen ein magne­tisches Feld, wobei im vorderen und hinteren Bereich Magnet­spulen konzen­trisch angeordnet sind. Diese Spulen bewirken ein nahezu homogenes Feld, welches diesen Glasbe­hälter durch­setzt. In dem Elek­tronen­strahl kann man sich jetzt noch einen Geschwindig­keits­vektor denken. In Achsrich­tung der Spulen verläuft ein magne­tischer Fluss­dichte­vektor . Dement­sprechend ergibt sich ein Kraft­vektor , der senkrecht auf beide zeigt. Aufgrund der Kraft­wirkung wird der Elektronen­strahl abgelenkt.

Wenn die Elek­tronen abgelenkt werden, ändert sich zunächst deren Geschwindig­keits­richtung. Und wenn sich die Richtung ändert, verändert sich auch die Anordnung des Kraft­vektors. Dennoch bleibt der Betrag der Geschwindig­keit generell immer konstant. Dement­sprechend wird sich die Bahn­kurve zu einer Kreis­bahn ausbilden. Bei einer Kreis­bahn ergibt sich eine konstante nach innen gerichtete Beschleunigung, auch Zentri­petal­beschleu­nigung genannt. Eine konstante zum Zentrum gerichtete Kraft hält die Teilchen auf einer Kreisbahn.

Wenn im weiteren Verlauf der Strom in der Spule erhöht wird, bildet sich auch ein größeres magne­tisches Feld aus. Demzu­folge wird auch die Kraft auf die Teilchen zunehmen. Und wenn die Kraft bei konstantem Geschwindig­keits­betrag anwächst, wird sich die Kreis­bahn stärker krümmen.

Zusätz­lich lässt sich der Glasbe­hälter mitsamt der Elektronen­kanone etwas schwenken. Dadurch wird erreicht, dass es eine kleine Komponente der Geschwindig­keit parallel zur magne­tischen Fluss­dichte gibt. Eine solche Geschwindig­keits­komponente, parallel zu erzeugt aller­dings keine Kraft, weil ein vekto­rielles Produkt Null ergibt. Demnach bleibt der Betrag einer solchen Komponente unver­ändert erhalten, und demzu­folge wird sich das Teilchen nicht auf einer Kreis­bahn bewegen, sondern auf einer Schrauben­bahn. Die Teilchen schrauben sich auf ihrer Bahn entlang der magne­tischen Feld­linien.

Wenn der Abstand der Helmholtz-Spulen gleich dem Radius der Spule ist, erzielt man ein besonders gutes homogenes Magnetfeld.

Die Kraft, die diese Wirkung hervorruft, wurde als Lorentz-Kraft definiert:

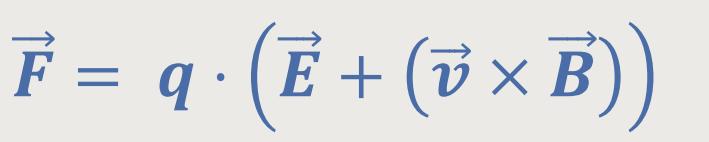
Wie sieht es mit den Dimensionen aus?

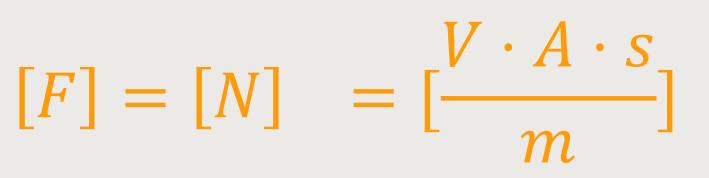
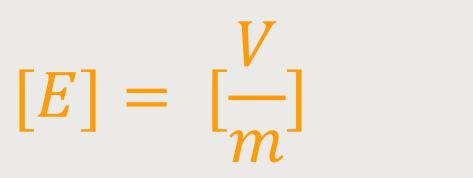
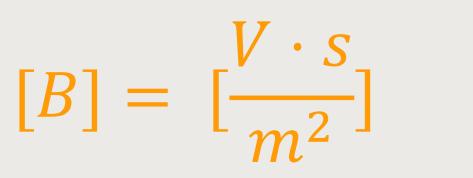
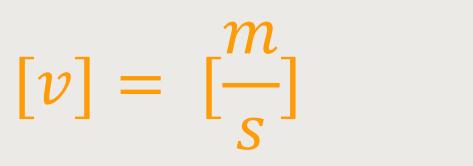
Wenn man diese Dimensionen jetzt in die Lorentz-Gleichung einsetzt, kann man erkennen, ob es alles aufgeht.

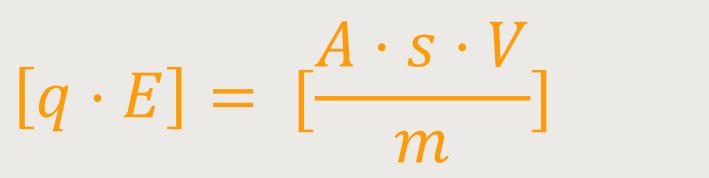
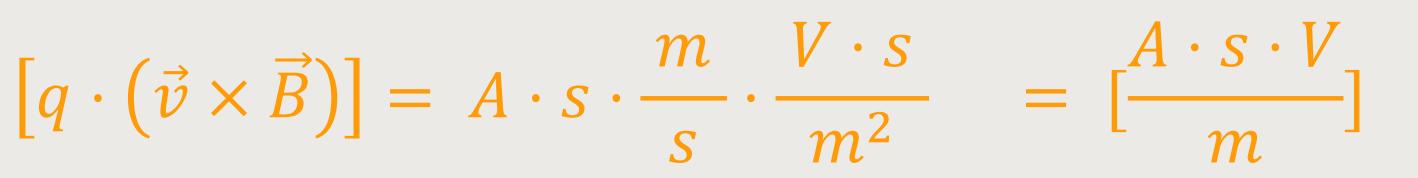
Damit stimmen die Dimensionen, sodass keine weiteren Feld­konstanten berück­sichtigt werden müssen. Erforder­liche Feld­konstanten finden sich nur in den Maxwell-Gleichungen und nicht in der Lorentz-Kraft.

Aus der Beobachtung der Kreis­bahn im Elektronen­strahl­rohr lässt sich eine wichtige Größe ermitteln. Denn wenn man den Radius der Kreis­bahn kennt, sowie die Geschwindig­keit und damit die Energie der Elektronen, und außerdem die Ladung eines Elektrons kennt, sowie die Größe der magne­tischen Fluss­dichte, kann man letzten Endes mit mecha­nischen Rechnungen aus der Zentri­petal­kraft die Größe e /m_e bestimmen.

e     ist die elektrische Elementarladung eines Elektrons
m_e   ist die Masse eines Elektrons

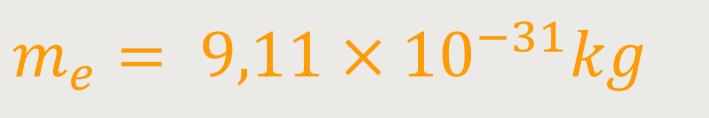
Das ist 1/1836 der Protonen­masse. Dieser Wert gilt aller­dings nur für v ≪ c_₀, also für klassische Bedingungen.

Im Nach­folgenden wird die Kraft auf einen strom­durch­flossenen Leiter in einem homogenen Magnet­feld ausgerechnet.

Grafik (wird später eingefügt)

A   ist die Leiter-Querschnittsfläche
q   ist die Ladung eines Ladungsträgers
n   ist die Anzahl der Ladungsträger pro Volumeneinheit
_D   ist die Driftgeschwindigkeit

Die Kraft auf ein kleines Leiter­stück dL stellt sich wie folgt dar:

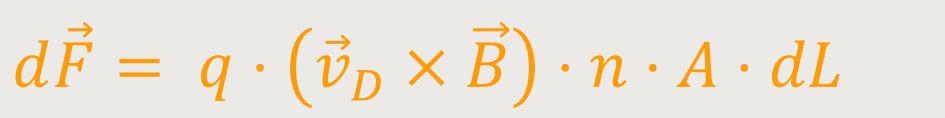
Für _D· dL kann man auch schreiben v_D · d . Man kann so vorgehen, weil beide den gleichen Betrag haben und parallel zueinander verlaufen.

Nun lässt sich diese Beziehung entsprechend umformen:

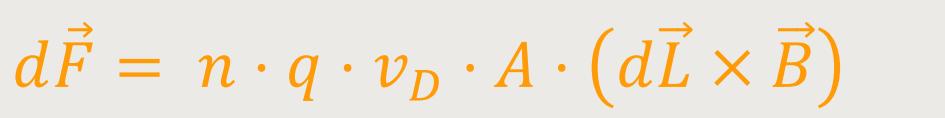
n · q    ist die Ladungs­dichte ϱ
ϱ · v_D   ist die Strom­dichte j
j · A    ist die Stromstärke I

Somit bleibt nur noch übrig:

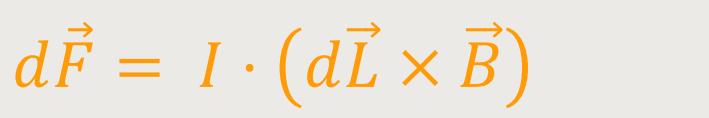
Damit erhält man eine sehr einfache Beziehung für die Kraft auf ein Leiter­stück, welches von einem Strom durch­flossen wird und sich in einem homogenen Magnet­feld befindet.

Diesen Formalismus kann man jetzt dazu verwenden, die Kraft­wirkung zwischen parallelen dünnen strom­durch­flossenen Leitern zu berechnen.

Grafik (wird später eingefügt)

Hierzu stellen wie uns zwei parallel verlaufende dünne strom­durch­flossene Leiter vor, mit einem Abstand d. Der erste Leiter umgibt sich mit einem magne­tischen Feld. Das bedeutet, dass sich der zweite Leiter im Magnet­feld des ersten Leiters befindet. Entspre­chend des Geschwindig­keits­vektors und dem magne­tischen Fluss­dichte­vektor erfolgt die Kraft­wirkung ausge­hend vom ersten auf den zweiten Leiter. Nun betrachtet man eine bestimmte Länge l_₂ des zweiten Leiters, die groß genug ist gegen­über deren Abstand.

Jetzt interessiert uns das Magnet­feld vom ersten Leiter an der Stelle des zweiten Leiters.

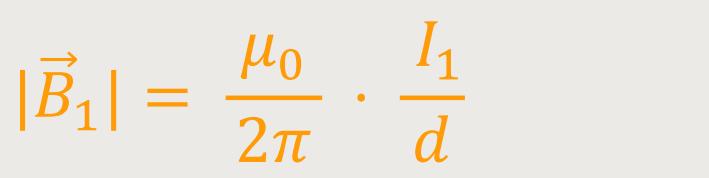
Die Kraft auf den zweiten Leiter stellt sich wie folgt dar:

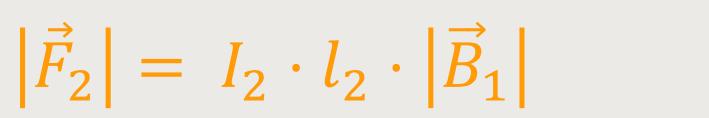
Nach Einsetzung erhält man:

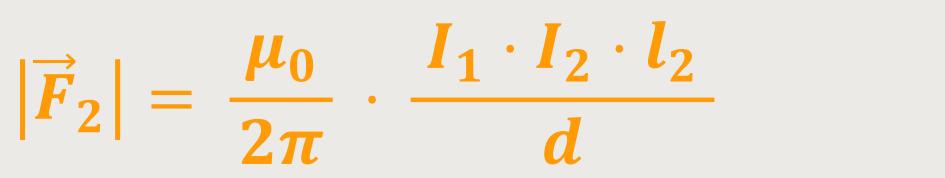
Das ist das Ampere'sche Kraftgesetz.

Der eine Leiter liefert das Magnet­feld, während sich der zweite Leiter sich in diesem Feld befindet.

Dieses Gesetz ist das magne­tische Gegen­stück zum Coulomb-Gesetz. Auf diese Weise lassen sich die Wechsel­wirkungen zwischen mehreren Strömen untersuchen.

Mit diesem Ampere'schen Kraft­gesetz definiert man letztlich die Einheit der Strom­stärke. Dazu kann man sich über­legen, was für eine Kraft wirken muss, wenn in beiden Leitern ein Strom von 1 Ampere fließt? Hierzu muss man ledig­lich die magne­tische Feld­konstante μ_₀ kennen. Definitions­gemäß beträgt diese Feldkonstante:

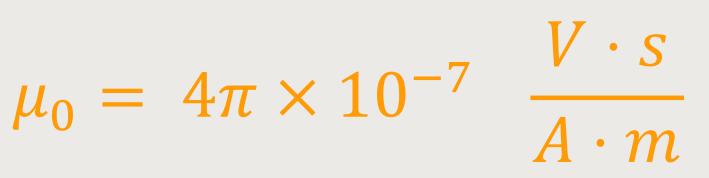
Wenn also l_₁ = l_₂ = 1A, und wenn l_₂ = d = 1m, dann ergibt sich für die Kraft auf den zweiten Leiter folgendes:

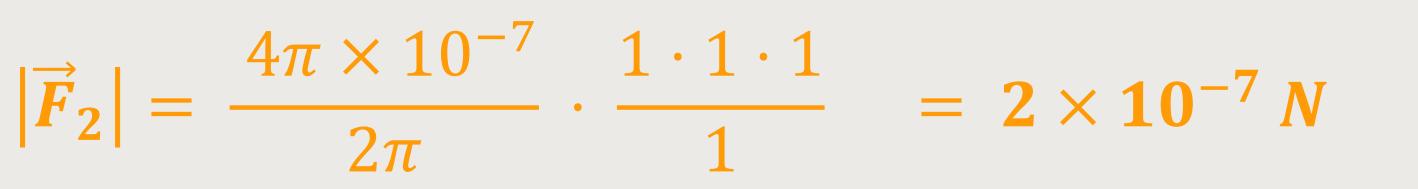
Wenn also in den beiden Leitern jeweils eine Strom­stärke von 1 Ampere durch­fließt, dann wird, wenn die Leiter einen Abstand von 1 Meter haben, auf einem Strecken­abschnitt von 1 Meter, auf den jeweils anderen Leiter eine Kraft von 2 × 10⁻⁷ N wirken.

Auf diese Weise lässt sich allein durch die mecha­nische Kraft­messung die elek­trische Strom­stärke­einheit ermitteln. So lautet die internationale Ampere-Definition.

⇦ Kapitel Kapitel ⇨