Jetzt geht es um die Eigen­schaften von Materie in magne­tischen Feldern. In der Regel hat die Materie, wenn man sie in ein Magnet­feld bringt, nur unwesent­liche Aus­wirkungen auf das magne­tische Feld. Anders verhält es sich dagegen bei ferro­magne­tischer Materie. Dort können die Aus­wirkungen mitunter sehr gravierend sein.

Der Sach­verhalt ist im Prinzip vergleich­bar mit der Beschrei­bung der Eigen­schaften von Materie bzw. Dielek­trika in elek­trischen Feldern. Dort gab es auch die Überlegung, dass die Moleküle, aus denen die Materie besteht, elek­trische Dipol­momente haben und sich entspre­chend ausrichten werden. Eine ähnliche Beschreibung lässt sich auch auf die magne­tische Materie übertragen.

Grund­sätz­lich kann Materie Träger eines magne­tischen Feldes sein. Also, wenn Materie in den Einfluss­bereich eines magne­tischen Feldes gelangt, wird das Feld im Allge­meinen diese Materie durch­setzen und kann durch die Materie selbst in irgend­einer Weise beeinflusst werden. Einer­seits kann die Materie eine Abschwä­chung verur­sachen, ähn­lich wie es bei Dielektrika in elek­trischen Feldern zu beobachten ist. Ander­seits kann durch ein Magne­tikum eine Verstär­kung des magne­tischen Feldes verur­sacht werden. Und wenn man zusätz­lich ein spezielles Ferro­magne­tikum einsetzt, kommt es zu erheb­lichen Verstär­kungen.

Als Ausgangs­punkt werden wir zunächst eine zylin­drische Spule im Vakuum betrachten.

Grafik (wird später eingefügt)

Durch eine zylin­drische Spule fließt ein Strom I. Zudem geht es um ein Rechts­system, in welchem die magne­tischen Fluss­dichte­vektoren _vac entspre­chend ausge­richtet sind.

Wir erinnern uns, laut des Ampere'schen Gesetzes ergibt sich:

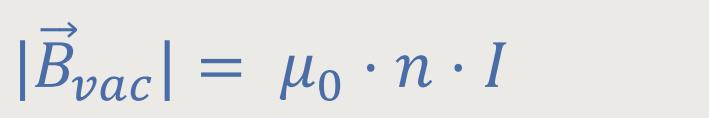
n   ist die Windungszahldichte (Anzahl der Windungen pro Längeneinheit)

Nun lässt sich noch einen Ersatz­term einführen, denn dieses n · I   ist der soge­nannte Spulen­ober­flächen­strom η pro Längen­einheit der Spule.

Durch Einsetzen erhält man:

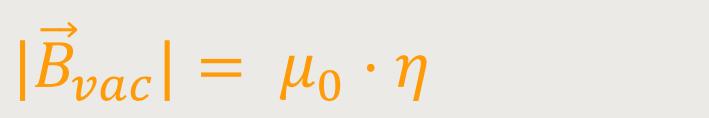
η   ist der Spulenoberflächenstrom pro Längeneinheit

Was passiert, wenn Materie in die betrachtete Spule einge­schoben wird?

Materie besteht aus Atomen oder Molekülen. Diese können sich ausrichten und haben im Allge­meinen ein magne­tisches Moment.

Grafik (wird später eingefügt)

Hierzu denken wir uns wieder eine zylin­drische Spule, durch die ein Strom I fließt. Nach wie vor geht es um ein Rechts­system. Diesmal wird aber zusätz­lich ein zylin­drischer Körper aus Materie in die Spule einge­führt. Die Moleküle in dem Körper werden sich jetzt entspre­chend des magne­tischen Flusses ausrichten.

Wenn es ein äußeres Vakuum­feld gibt, werden sich vorhan­dene magne­tische Dipole unter der Wirkung des äußeren Magnet­feldes so ausrichten, dass die magne­tischen Dipol­momente parallel und zu den Fluss­dichte­vektoren gleich­gerichtet sein werden. Diese Vektoren sind den Feld­vektoren entgegen­gerichtet, was zu einem kleineren magne­tischen Feld führt.

Dadurch wird die Orientierungs­richtung der Kreis­ströme für jeden Dipol gleich­sinnig mit der Orientierungs­richtung des Stroms durch die Spule sein. Es folgt also eine Polari­sation der Materie durch Ausrichtung der moleku­laren Dipole.

Grafik (wird später eingefügt)

Durch die Anwesen­heit des Materie­stücks wird sich eine Verände­rung des magne­tischen Feldes einstellen. Und so wird aus der magne­tischen Fluss­dichte _vac im Vakuum ein _mat in der Materie.

Wie schaut jetzt die Magnetisierung in der Materie aus?

Bei den elek­trischen Eigen­schaften wurde bereits über die Polari­sation des Dielektrikums gesprochen. Als Analogie spricht man jetzt aber nicht von der magn­etischen Polari­sation, sondern von der „Magneti­sierung”. Darunter versteht man die Summe aller Dipol­momente pro Volumen­einheit. Daher ergibt sich für die Magneti­sierung:

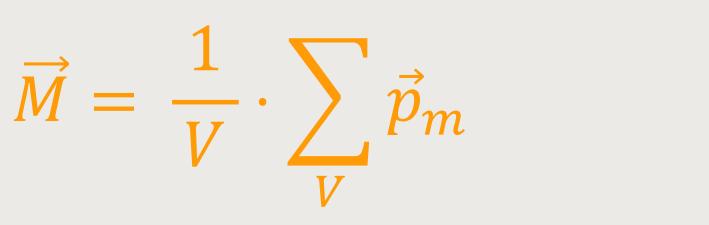
V   ist das Volumen der Materie

Bei paralleler Ausrich­tung aller magne­tischen Dipole stellt sich der Betrag wie folgt dar:

N   ist die Anzahl der Moleküle pro Volumeneinheit
  ist der Flächenvektor des Dipolmoments
i   ist der Strom, der um den Dipol herum fließt

Es gilt zu beachten, dass die Kreis­ströme im Innern des Zylinder­blocks so liegen, dass sich diese Kreis­ströme in ihren magne­tischen Wirkungen alle gegen­seitig kompen­sieren. Nur außen bleibt ein Polari­sations­strom in der Zylinder­ober­fläche erhalten.

Wie lässt sich dieser Polari­sations­strom abschätzen?

1 / N   ist das Volumen eines Moleküls
1 / (N · A)   ist die Querdimension eines Dipolmoleküls (Höhe)
N · A   ist die Anzahl der Molekülschichten pro Längeneinheit

Insofern lässt sich dieser Polari­sations­strom näherungs­weise wie folgt ausrechnen:

Mit dieser Ausgangs­situation kann man auch das magne­tische Polari­sations­feld ausrechnen:

Wie lässt sich aus dieser Betrags­gleichung die zuge­hörige Vektor­gleichung darstellen? In diesem Zusammen­hang unter­sucht man die Lage der Felder.

Grafik (wird später eingefügt)

Das magne­tische Polari­sations­feld _pol ist parallel und gleich­sinnig ange­ordnet zu den äußeren magne­tischen Fluss­dichte­vektoren _vac. Das ist ein wesent­licher Unter­schied gegen­über elek­trischen Eigen­schaften eines Dielektrikums. Des Weiteren sind auch alle magne­tischen Dipol­momente der einzelnen Moleküle in der gleichen Richtung ausge­richtet. Insofern zeigt auch die Magneti­sierung in die Fluss­richtung.

Mit anderen Worten, das Magnet­feld wird durch die Anwesen­heit des polari­sierten Magnetikums verstärkt. Und wenn alles gleich ausge­richtet ist, kann man die Betrags­striche weglassen und es ergibt sich:

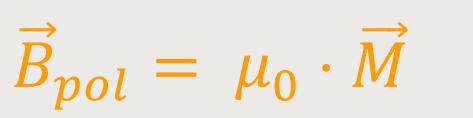
Damit lässt sich das Magnet­feld in der Materie ausrechnen:

Was bedeutet das konkret? Hierzu wird die Magneti­sierung pro Volumen­einheit benötigt. Bei der Polari­sation der Materie gibt es zum Beispiel auch den Diamagne­tismus. Was versteht man darunter?

Es gibt nicht nur Körper, die bereits magne­tische Dipol­momente aufweisen, sondern auch Körper, dessen Moleküle zunächst gar kein magne­tisches Dipol­moment besitzen. Sie werden erst eines erhalten, wenn man den Spulen­strom einschaltet. Aufgrund des veränder­lichen magne­tischen Flusses wird im Innern des Moleküls eine Spannung induziert. Der Strom, der sich dann ergibt, wird dem induzie­renden äußeren Vakuum­feld entgegen­gerichtet sein, wodurch das Feld geschwächt wird.

In diesem Fall wird ein magne­tisches Dipol­moment induziert, welches dem ursprüng­lichen Feld entgegen­gerichtet ist. Mit anderen Worten, die induzierten Dipol­momente werden jetzt, anders als zuvor betrachtet, das magne­tische Feld abschwächen. Das ist der sogenannte „Diamagnetismus”.

Die Verstärkung des magne­tischen Feldes nennt man dagegen den „Paramagnetismus”. Und wenn wir ein Material haben, in welchem sich die Moleküle besonders gut ausrichten lassen, spricht man von dem „Ferro­magnetismus”.

Es zeigt sich experi­mentell, dass die Magneti­sierung propor­tional zur Fluss­dichte des Vakuums ist:

Des Weiteren ist die Magneti­sierung gleich einem Propor­tionalitäts­faktor pro Volumen­einheit:

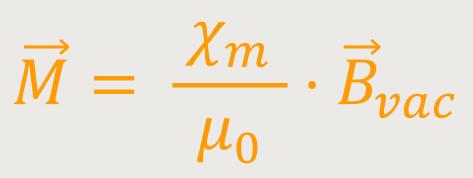
Χ_m   ist die magne­tische Suszeptibilität

Dieser Faktor ist abhängig von dem jeweiligen Material.

Und wenn man das entspre­chend einsetzt, erhält man jetzt für das Magnet­feld der Materie:

Vereinfacht ausgedrückt, schreibt man auch:

μ_r   ist die relative magnetische Permeabilität

Zusammen­fassend bedeutet das, dass die magne­tische Fluss­dichte um den Faktor μ_r verändert wird. Je nach Material bzw. bei Anwesen­heit eines Magne­tikums wird die magne­tische Fluss­dichte entweder verringert oder verstärkt. Oder anders ausge­drückt, wenn die magne­tische Suszepti­bilität < 0, wird das μ_r < 1 und damit das Feld abge­schwächt. Wenn die magne­tische Suszepti­bilität dagegen > 0, wird das μ_r > 1, und damit wird das Feld in der Materie verstärkt.

Beispiele für Diamagnetismus

Tabelle (wird später eingefügt)

⇦ Kapitel Kapitel ⇨