Wenn man Schalt­vor­gänge bei Spulen untersucht, insbesondere den Ausschalt­vorgang, lässt sich beobachten, dass nach dem Ausschalten der Strom noch eine Zeitlang weiter­fließt. Hinter dieser Beobachtung muss irgen­deine Energie stecken, damit die Spule dazu in der Lage ist. Die Ursache liegt darin, dass neben dem elek­trischen Feld auch das magne­tische Feld einen Energie­gehalt hat.

Grafik (wird später eingefügt)

Vor dem Schaltvorgang ist der Stromstärke zum Zeitpunkt t = 0 definiert als:

Nach dem Schalt­vorgang sieht die Situation wie folgt aus:

Wir erinnern uns, laut Induktions­gesetz ist die induzierte Spannung definiert als:

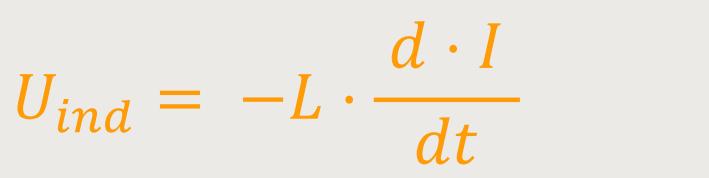
Des Weiteren erinnern wir uns, dass laut 2. Kirchhoff-Gesetz die induzierte Spannung definiert ist als:

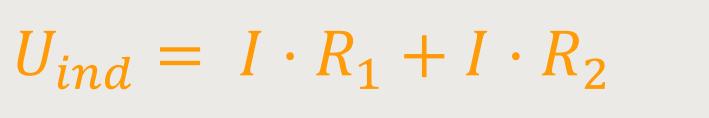
Wenn man R = R_₁ + R_₂ setzt, ergibt sich:

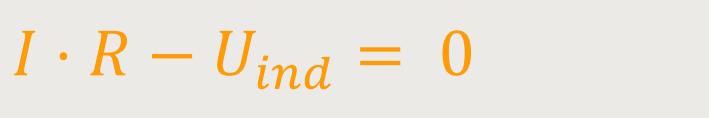
Wenn man diese Beziehung in das Induktions­gesetz einsetzt, erhält man folgende Differential­gleichung:

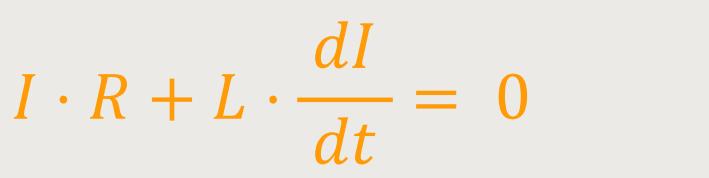
Weil es sich hierbei um eine homogene Differential­gleichung handelt, kann man eine Trennung der Variablen durchführen:

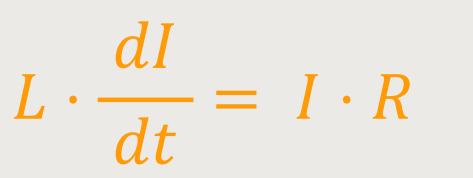
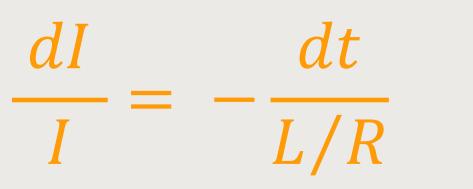
Nach Integration ergibt sich:

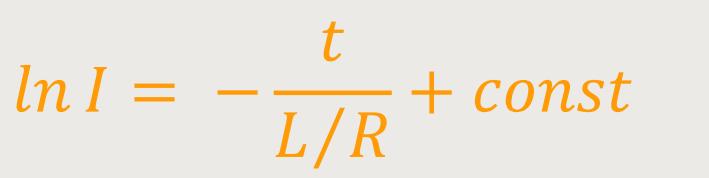
Um eine Integrations­konstante zu erhalten, schaut man sich die Anfangs­bedingungen an:

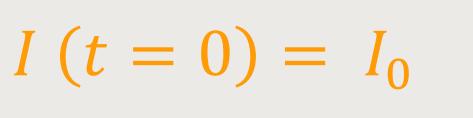
Daraus folgt:

Als Ergebnis erhält man:

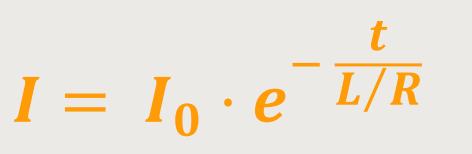
Dieses L /R muss auch die Dimension einer Zeit haben, damit der Exponent dimensionslos bleibt. Daraus folgt, dass man eine Zeit­konstante angibt, die definiert ist als:

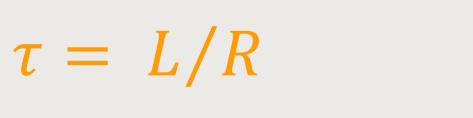
Diese Zeitkonstante besagt, wenn t = τ, dann erhält man e ⁻¹.

Grafik (wird später eingefügt)

Jetzt interessiert uns noch, was mit der Spannung an der Spule passiert.

Grafik (wird später eingefügt)

Aber woher nimmt die Spule die Energie, damit sie bewirken kann, dass der Strom noch eine Zeitlang weiter­fließt?

Ausgangs­punkt ist die oben erarbeitete Gleichung:

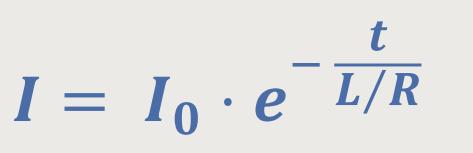
Wir betrachten jetzt, wie es sich mit der Energie verhält, die beim Ausschalt­vorgang in dem Ohm'schen Wider­stand verbraucht wird.

Die verbrauchte Energie lässt sich wie folgt ausrechnen:

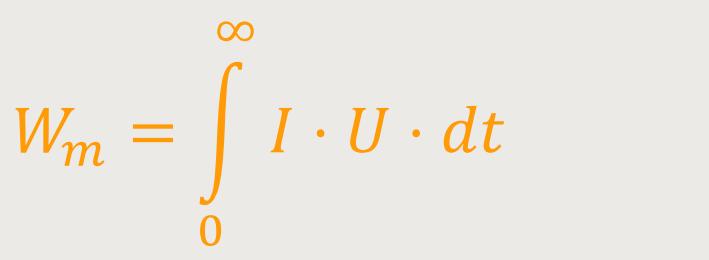
W_m   ist die geleistete Arbeit (magnetisch)

Unter Berück­sichtigung des Ohm'schen Gesetzes kann man auch schreiben:

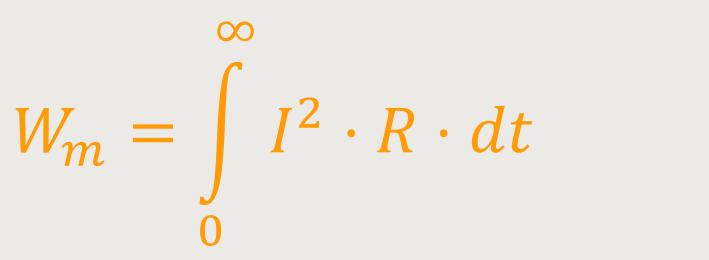
Und wenn man jetzt die Beziehung für den Strom einsetzt, ergibt sich:

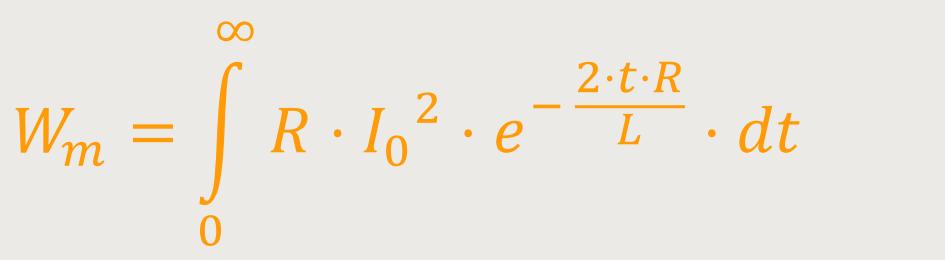
Für die weitere Integration wird durch Substitution der ganze Exponent durch u ersetzt:

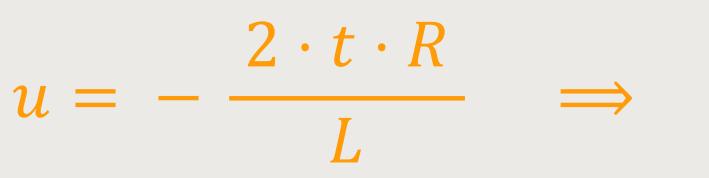
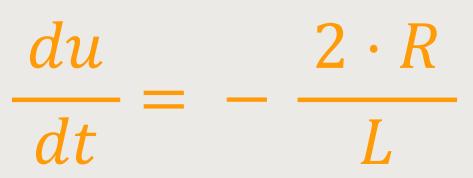
Dann ergibt sich für das dt durch Umstellen:

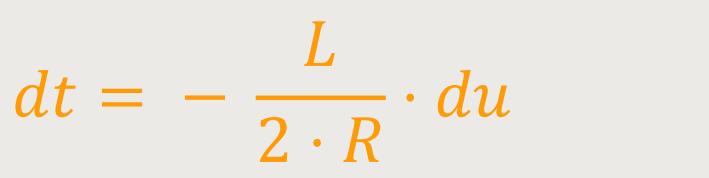
Damit erhält man durch Einsetzen für das Integral:

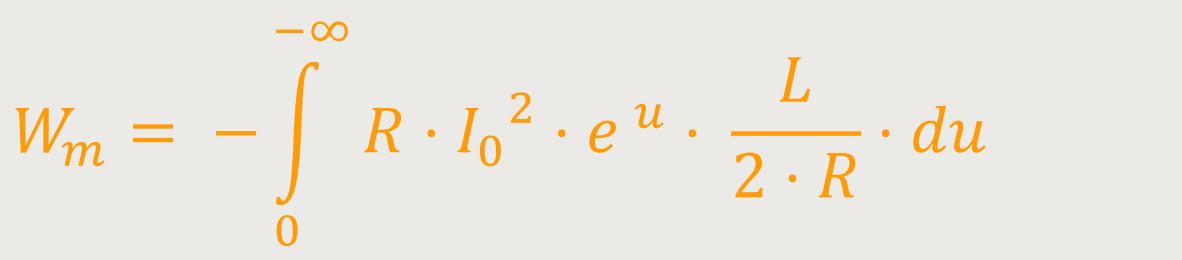
Wenn nun noch die Konstanten vor das Integral gesetzt werden, bleibt stehen:

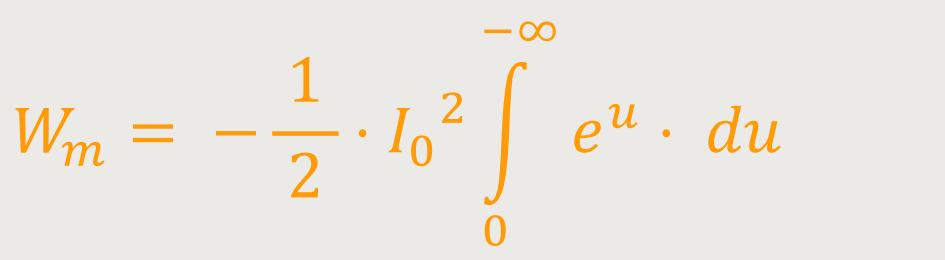
Damit ist die Stamm­funktion e^u, was für das Integral bedeutet:

Nun über­tragen wir das Ganze auf eine idealisierte zylin­drische Spule.

Wir erinnern uns, die Induktivität war definiert als:

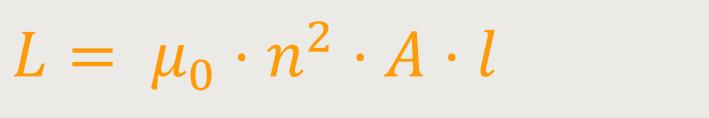
Ander­seits gilt für die magne­tische Fluss­dichte im Inneren dieser Spule:

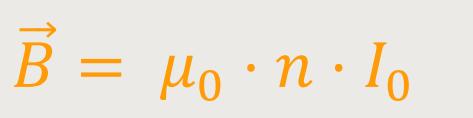
Damit erhält man für die Arbeit (magnetisch) bzw. Energie durch Einsetzen:

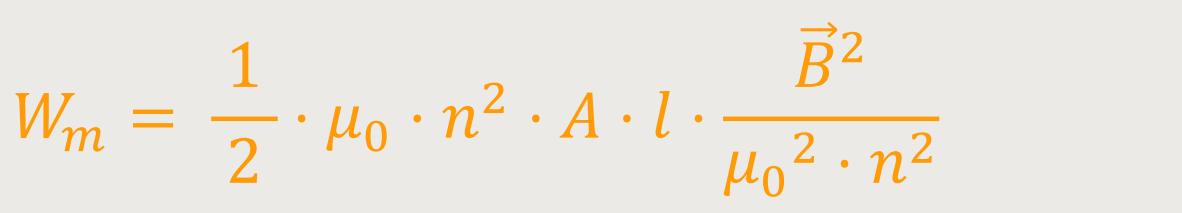
Nach Wegkürzen erhält man:

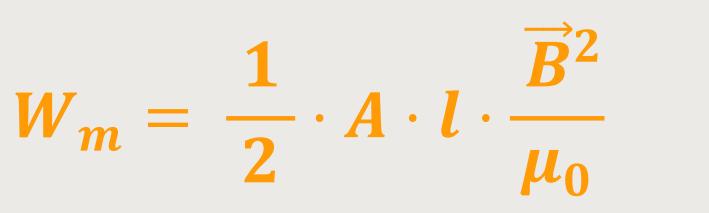
Das ist die Energie, die im Inneren der Spule steckt. Und hier kann man erkennen, dass die Energie in dem Volumen der Spule gespeichert wurde.

A · l   ist das Feldvolumen

In diesem Volumen befindet sich das gesamte Magnet­feld. Auf diese Weise lässt sich die Energie des Magnet­feldes pro Volumen­einheit ausrechnen.

Die Energie­dichte dieses Magnet­feldes ergibt sich als:

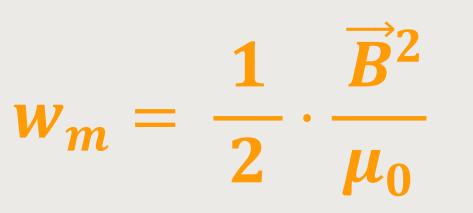
Wir erinnern uns, die Energie­dichte des elek­trischen Feldes wurde definiert als:

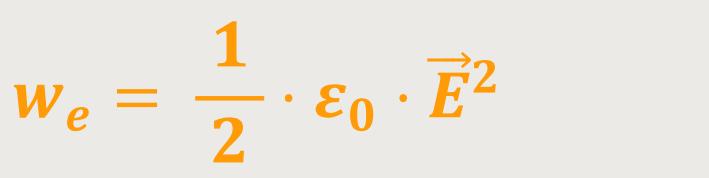
Und damit lässt sich abschließend die Energie­dichte es gesamten elektro­magne­tischen Feldes definieren:

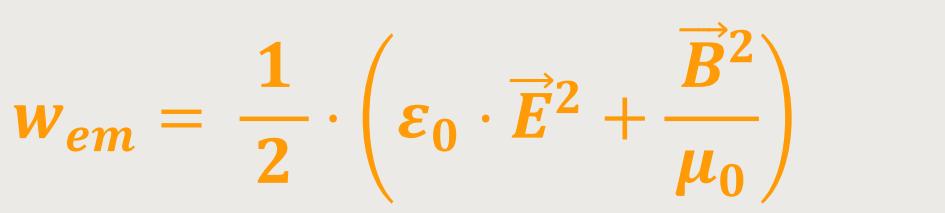
Diese Energiedichte ist dafür verant­wortlich, dass mit den elektro­magne­tischen Wellen Energie über­tragen werden kann. Denn in elektro­magne­tischen Wellen sind gleicher­maßen zeitlich veränder­liche elektrische und magnetische Feld­vektoren enthalten. Und wenn sich die Wellen­felder ausbreiten, breitet sich mit diesen Feldern auch die Energie aus.

⇦ Kapitel Kapitel ⇨