Die nach­folgende Betrach­tung dient als Grund­lage um zu verstehen, warum es elektro­magne­tische Wellen gibt. Denn elektro­magne­tische Wellen sind ein sehr wichtiges Modell, mit dem sich unter anderem die Licht­ausbreitung beschreiben lässt.

Wir erinnern uns, das Ampere'sche Gesetz sagt aus, dass die magne­tische Spannung längs einer geschlossenen Schleife oder Spule gleich dem elek­trischen Strom ist, der von dieser Schleife einge­schlossen wird:

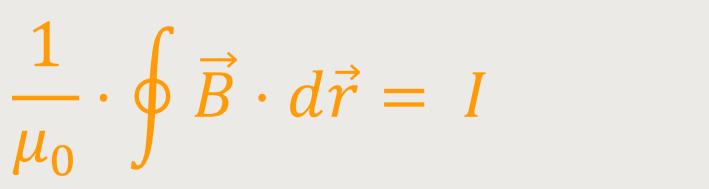
Eine andere Schreibweise lautet:

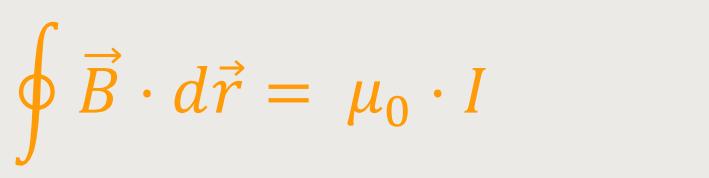
Daraus ergab sich als Folgerung die 2. Maxwell-Gleichung:

Gleichungen haben aber nur dann ihre Gültig­keit, wenn diese auf ihre Schlüssig­keit geprüft worden sind. Und so kam man bei dieser Maxwell-Gleichung auf die Idee, die Divergenz zu bilden.
Hinweis: Die Vektor­differential­operatoren spielen immer wieder eine wichtige Rolle.

Und so ergibt sich:

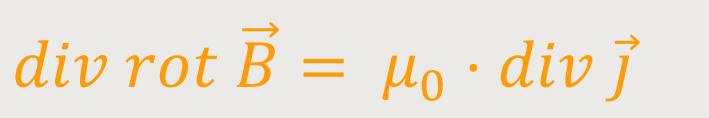
Da aber stets div rot = 0 ist und es ich bei μ_₀ um eine Konstante handelt, folgt daraus:

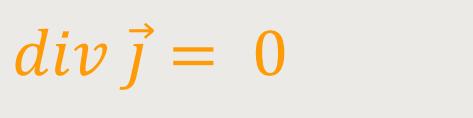
Wie schon mehrfach erwähnt, ist die Ladungs­erhaltung eine wesent­liche Grund­lage in der Elektro­dynamik. Diese Ladungs­erhaltung kann ebenso dar­gestellt werden wie die Massen­erhaltung in der Hydro­dynamik. Das geschieht im All­gemeinen durch eine Kontinuitäts­gleichung:

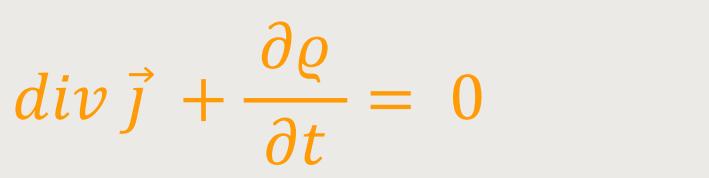
Wenn div > 0, dann gibt es einen Netto-Strom­fluss aus einem Volumen heraus, wobei die Ladungs­dichte zurück­geht. Bei genauer Betrach­tung stellt man fest, dass die unter­schied­lichen Divergenz-Bildungen jeweils zu Null führen.

Das würde aber bedeuten, dass immer ∂ϱ / ∂t = Null ist. Und damit wäre unsere Welt total statisch und es könnte sich niemals eine Ladungs­dichte verändern. Da das natür­lich in dieser Form nicht sein kann, kommt es auf den ersten Blick zu einem ernsten Wider­spruch. Also, was bedeutet das? Entweder stimmt die Ladungs­erhaltung nicht oder es stimmt etwas nicht mit der Ladungs­dichte.

Wenn man aber sinn­voller Weise davon ausgehen kann, das die Ladungs­erhaltung stimmt, dann muss die 2. Maxwell-Gleichung erweitert werden, damit die Ladungs­dichte ≠ Null ist.

Um das zu unter­mauern, wollen wir gedank­lich ein Experiment durch­führen.

Hierzu betrachten wir einen Strom­kreis mit einem Platten­konden­sator. Der Konden­sator soll entweder aufge­laden oder entladen sein. Um das zu erreichen, legt man eine zeit­lich wechselnde Spannung an. Dadurch wird der Konden­sator einmal in der einen und einmal in der anderen Richtung aufge­laden. Wir betrachten jetzt genau den Zeit­punkt während eines Auflade-Vorgangs.

Es sei erwähnt, dass trotz des Dielek­trikums − hier soll es ein Vakuum zwischen den Konden­sator­platten sein − ein Lade­strom fließen wird. Und wenn solch ein Lade­strom fließt, wird sich auch ein Magnet­feld ausbilden. Gemäß dem Ampere'schen-Gesetz entsteht in Folge dessen rund­herum ein magne­tischer Feld­wirbel K_₁ mit einem Radius r.

Was wird passieren, wenn man jetzt einen weiteren Kreis K_₂ zwischen die Konden­sator­platten einfügt. Zunächst würde man davon ausgehen, dass sich dort kein magne­tischer Feld­wirbel ausbildet, weil ja im Dielek­trikum kein elek­trischer Lade­strom fließt. Dem ist aber nicht so, denn in der Realität zeigt sich, dass es auch zwischen den Platten einen gleich­artigen magne­tischen Feld­wirbel gibt.

Mittels Ampere'schen-Gesetz lässt sich der magne­tische Feld­wirbel K_₁ berechnen:

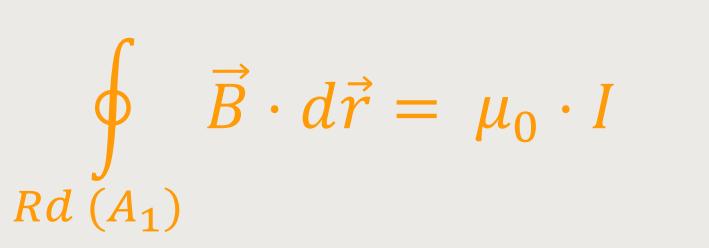
Das Ring­integral ist, wie wir bereits wissen, gleich dem Kreis­umfang multi­pliziert mit dem Vektor­feld (betrags­mäßig):

Andererseits lässt sich mittels Ampere'schen-Gesetz genauso K_₂ berechnen:

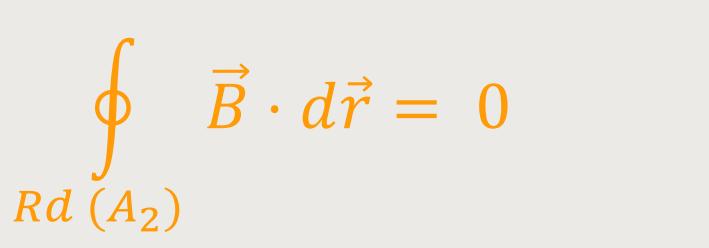
Da nichts einge­schlossen wird, ist das Ring­integral in diesem Fall Null.

Das ist aber ein Wider­spruch zum experimen­tellen Befund. Somit führt das Ampere'sche-Gesetz hier nicht zum Ziel.

Es gibt aller­dings eine interes­sante Über­legung. Bei dem Ampere'schen-Gesetz heißt es ja nur, dass längs einer geschlossenen Kurve integriert wird, durch die ein Strom hindurch­tritt. Es wird aber nicht gesagt, dass diese Fläche, um deren Rand es geht, eine ebene Fläche sein muss. Man kann ja auch eine Art Glocke betrachten, also eine gewölbte Fläche, die in das Dielektrikum hinein­reicht. Eine solche Fläche _₁ lässt sich auch als Ring-Integral darstellen.

Mittels Ampere'schen-Gesetz lässt sich das verän­derte K_₁ berechnen:

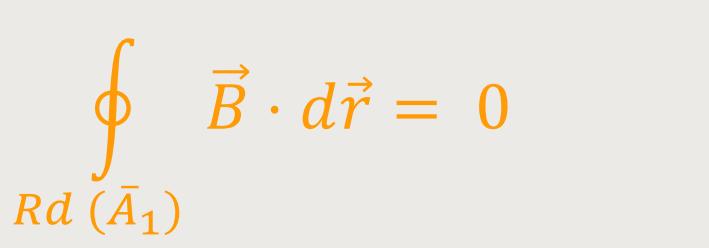
Damit erhalten wir aber einen Wider­spruch sowohl zum obigen Ergebnis als auch zum Experiment.

Um dieses Problem zu lösen, hatte Maxwell die Idee, einen zusätz­lichen imaginären Strom einzuführen. Dabei handelt es sich um den sogenannten Maxwell'schen Verschie­bungs­strom. Hierbei geht es um einen Zusammen­hang zwischen dem Strom einer­seits und der Ände­rung der Ladungen auf den Konden­sator­platten anderer­seits.

Die Ände­rung der Ladung ergibt sich aus dem Strom in den Zuleitungen:

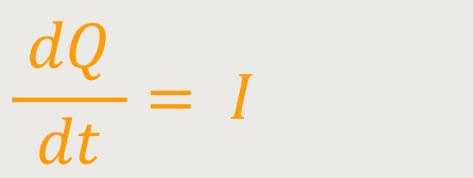
Jetzt wird ein imaginärer Strom zwischen den Konden­sator­platten einge­führt, so als würde dort ein Strom fließen, was aber in Wirklich­keit nicht der Fall ist. Aus diesem Grund wird der Verschie­bungs­strom I_v mit dem Lade­strom I gleich­gesetzt:

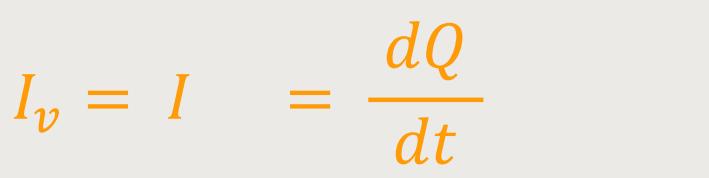
Wir erinnern uns, dass die Ladung ist definiert als:

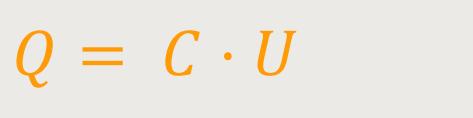
Und die Kapazität ist definiert als:

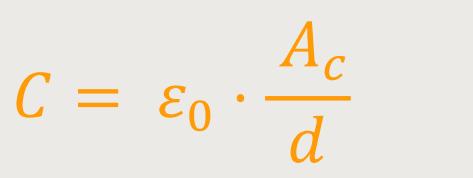
d    ist die Distanz zwischen den Konden­sator­platten
A_c   ist die Fläche der Konden­sator­platten

Durch Einsetzen ergibt sich daher:

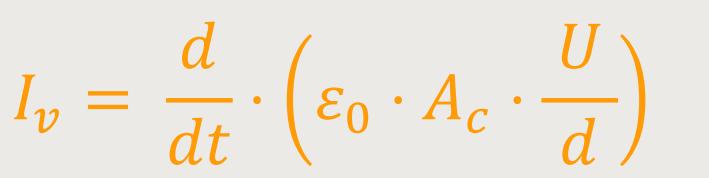
U /d   ist der Betrag der elek­trischen Feld­stärke E

Daher kann man auch schreiben:

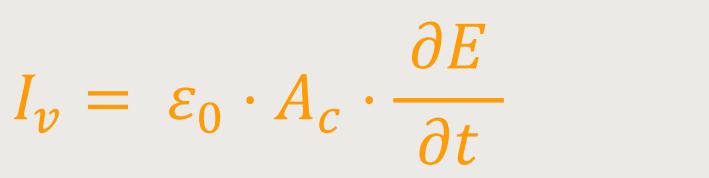
Hier wurde eine partielle Schreib­weise gewählt, weil die elek­trische Feld­stärke auch von den Orts­koordinaten abhängig ist.

Natürlich lässt sich das auch vektoriell schreiben, indem man die Platten­fläche mit einem Flächen­vektor _c beschreibt. In diesem Fall lässt sich der Verschie­bungs­strom vektoriell darstellen als:

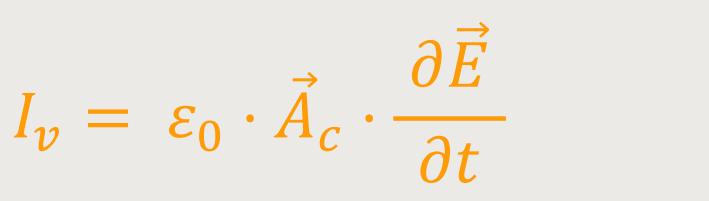
Auf diese Weise steht nicht mehr die Ladung im Vorder­grund, sondern die zeit­liche Ände­rung des elek­trischen Feldes. Wenn sich das elek­trische Feld zwischen den Platten ändert, also wenn sich der Konden­sator auflädt oder entlädt, dann kommt es zu einem Verschie­bungs­strom. In unserem Fall ist dieser Verschie­bungs­strom gleich­bedeutend mit dem tatsäch­lich fließenden Ladungs­strom.

Im nächsten Schritt wird zu dem Ladungs­strom I, der nur die Zu- und Ableitung betrifft, der Verschie­bungs­strom I_v hinzu­gefügt, der seiner­seits nur den Bereich zwischen den Konden­sator­platten betrifft. Durch diese Vorgehens­weise sieht es so aus, als wenn der elek­trische Strom stetig und ohne Unter­brechung durch die gesamte Anordnung fließt.

Damit wird dem Verschie­bungs­strom I_v jetzt die gleiche magne­tische Wirkung zuge­schrieben, wie dem tatsäch­lichen Strom. Und daher erhält das Ampere'sche Gesetz einen anderen, allge­meineren Formalismus:

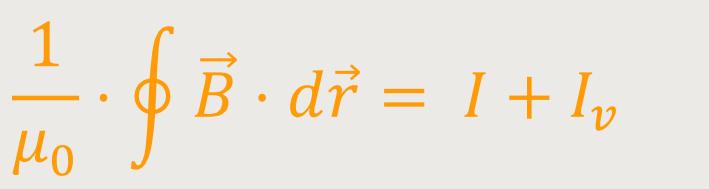
Wenn man diese Beziehung umformen und in eine differen­tielle Schreib­weise bringen möchte, benötigt man von dem Verschie­bungs­strom zunächst die zugehörige Dichte.

Die Verschie­bungs­strom­dichte ist definiert als:

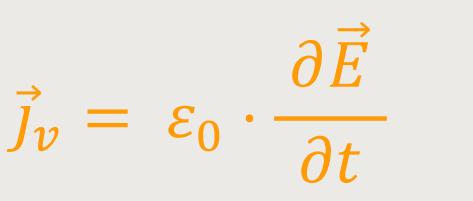
Das heißt, wenn sich in dem Konden­sator das Feld nicht ändert, dann ist die Verschie­bungs­strom­dichte Null. In diesem Fall fließt außer­halb kein Strom, und dann entsteht auch kein magne­tisches Feld. Natür­lich betrachten wir hier einen ideali­sierten Konden­sator mit unendlich großen Platten bei einem geringen Abstand.

Dadurch erhält man auch eine allgemeinere Maxwell-Gleichung:

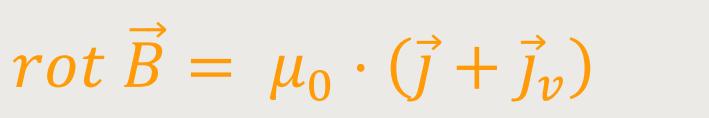
Durch Einsetzen ergibt sich:

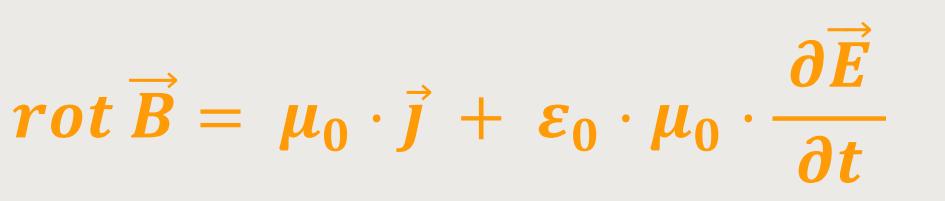
Hinweis: Der zweite Term entspricht dem Maxwell'schen Verschie­bungs­strom.

Warum nennt man ihn aber Verschie­bungs­strom, wenn doch tatsäch­lich gar kein Strom fließt? Das wird anhand dieser Gleichung klar. Nämlich, ein magne­tischer Feld­wirbel wird nicht nur durch einen Strom­fluss bewirkt, sondern zusätzlich und unabhängig davon auch von einem zeitlich veränderlichen elek­trischen Feld.

Und damit gibt es in Wirklich­keit zwei Ursachen für die Ausbildung eines magne­tischen Feld­wirbels. Um zu erkennen, ob diese neue Beziehung stimmig ist, bildet man erneut die Divergenz.

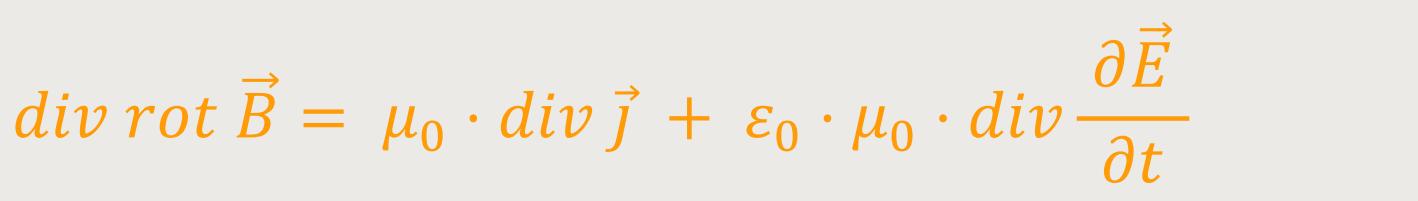
Hinweis: Räum­liche und zeit­liche partielle Differen­tiationen können hierbei ausge­tauscht werden, wenn diese ausreichend definiert sind. Daher kann man auch schreiben:

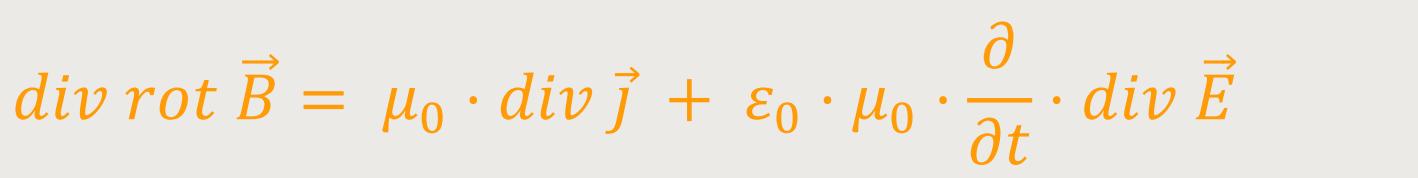
Das ist praktisch, denn die 1. Maxwell-Gleichung gesagt ja, dass:

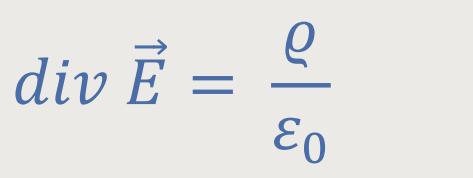
Außerdem ist, wie allgemein bekannt:

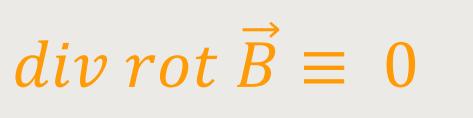
Durch Einsetzten ergibt sich daher:

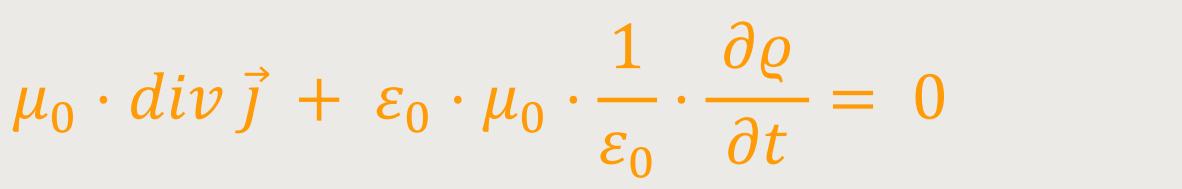
Nach Wegkürzen bleibt schließlich nur noch übrig:

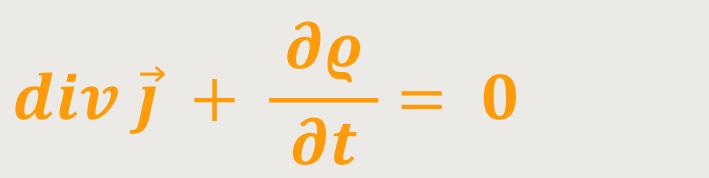
Und genau das ist die Kontinui­täts­gleichung, die der Ladungs­erhaltung entspricht.

Damit sind alle Wider­sprüche geklärt, und man kann ohne Weiteres aus der 2. Maxwell-Gleichung die Divergenz bilden.

Alles in allem ist die Kontinui­täts­gleichung bzw. die Ladungs­erhaltung in die Maxwell-Gleichung mit eingebaut. Daher kann die Kontinui­täts­gleichung auch als eine „Konsistenz­bedingung” aufgefasst werden: „Nur wenn die Ladungs­dichten und die Strom­dichten miteinander konsistent sind, bleibt es bei einer Ladungs­erhaltung.”

Insgesamt haben wir nun vier Maxwell-Gleichungen aus experimen­tellen Befunden gewonnen.

Wir haben zwei inhomogene Gleichungen:

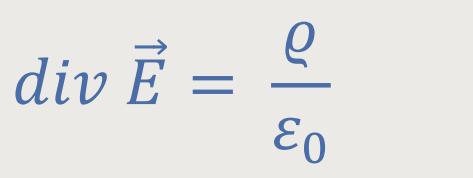
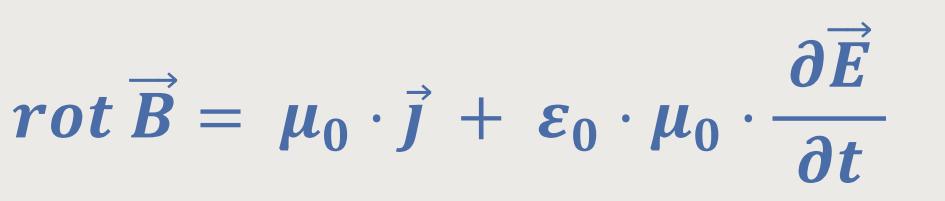
Man bezeichnet beide als inhomogen, weil sie die Ladungs­dichte und die Strom­dichte enthalten.

Und wir haben zwei homogene Gleichungen:

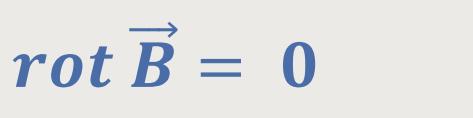
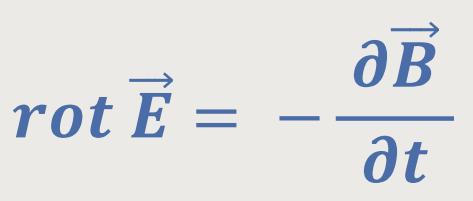
In dem negativen Vorzeichen wird die Energie­erhaltung ausgedrückt.

Zu diesen vier Maxwell-Gleichungen kommt die bereits betrachtete Lorentz­kraft. Bei vorge­gebenen ϱ und lassen sich elek­trische und magne­tische Felder ermitteln. Sind die Felder bekannt, lässt sich mittels der Lorentz­kraft die Kraft­wirkung auf andere Fluss­dichten darstellen.

Wir hatten die Lorentz­kraft bereits definiert als:

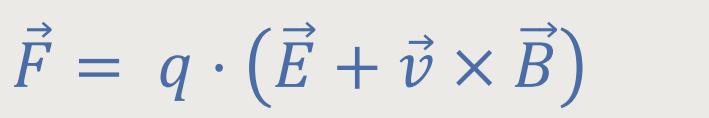
Diese fünf Gleichungen stellen die gesamte elektro­magne­tische Wechsel­wirkung dar und bilden die Basis für die klassische Feld­theorie der Elektro­dynamik. Wenn man obige Maxwell-Gleichungen auf ein gleich­förmig bewegtes Bezugs­system trans­formiert, kommen Gleichungen mit zusätz­lichen Termen heraus, die proportional zu v_² / c_₀² sind. Doch dazu später mehr.

Dieser Effekt scheint auf den ersten Blick sehr unangenehm, doch die zusätz­lichen Terme haben keinen Einfluss mehr auf die Maxwell-Gleichungen. Vielmehr wurde es notwendig, die Newton'sche Mechanik zu reformieren. Und das führte schließlich zur Speziellen Relativitäts­mechanik.

⇦ Kapitel Kapitel ⇨