Jetzt wenden wir uns den zeitab­hängigen Magnet­feldern zu, bei denen neue Phäno­mene in Erschei­nung treten. Wir werden uns aller­dings nur auf Zeitab­hängig­keiten beschränken, die verhältnis­mäßig langsam ablaufen. Das bedeutet, dass die typischen Änderungs­zeiten für die betrach­teten Vorgänge lang sind, im Verhältnis zu den Ausbreitungs­zeiten der elektro­magne­tischen Wellen.

Das hat den Vorteil, dass unter­schied­liche Rahmen­bedingungen ein­heitlich betrachtet werden können. In der Realität erfolgt die Ausbrei­tung elektro­magne­tischer Wellen und elektro­magne­tischer Felder blitzartig. Derartige endliche Verzöge­rungen werden wir nach­folgend vernach­lässigen, und quasi im Vergleich dazu „schnecken­haft” langsame Verände­rungen betrachten.

Wenn man zum Beispiel einen Permanent­magneten durch eine Spule fallen lässt, während diese nur an einem Oszilloskop ange­schlossen ist, entsteht trotzdem ein Signal in Form einer Schwingung, obwohl kein Strom fließt. Was ist die Ursache für diesen Effekt? Nun, wenn der Magnet in die Nähe der Spule kommt, steigt das magne­tische Feld bei Eintritt an, und wenn der Magnet wieder austritt, sinkt das Feld wieder ab. Die Schwingung im Oszilloskop schlägt zunächst einseitig aus. Auf der Gegen­seite fällt der Ausschlag der Schwingung höher aus, was je nach Spulenan­ordnung mit der höheren Fall­geschwindig­keit des Magneten beim Durch­lauf zu tun hat.

Beim Ansteigen und beim Abfallen des Feldes macht sich an der Spule eine Spannung bemerkbar. Man bezeichnet das auch als „indizierte Spannung”. Die Höhe des Signals bzw. der Amplitude ist propor­tional zur Änderungs­geschwindig­keit des Magnet­feldes. Je schneller es sich ändert, desto höher werden die Signale.

Wenn man mit zeitabhängigen magne­tischen Feldern zu tun hat, treten neue Effekte auf. Wie das Beispiel zuvor beschrieben, bewirkt ein Permanent­magnet im freien Fall, der durch eine Spule hindurch­tritt, dass an den Enden dieser Spule eine Spannung messbar wird. Diese Induktions­spannung ist propor­tional zur Geschwindig­keit der Bewegung.

Die Spannung, die in so einem Leiter­kreis (Spule) entsteht, hängt davon ab, wie schnell sich das magne­tische Feld ändert.

Das Integral über den Spannungs­impuls ist unabhängig von der Geschwindig­keit der Bewegung. Eine höhere Geschwindig­keit bedeutet eine höhere Induktions­spannung, aber nur einen halb so breiten Impuls.

Anderer­seits hat die Fläche, die von einem Leiter­kreis umschlossen wird, Ein­fluss auf die Spannung. Insbe­sondere dann, wenn das Magnet­feld konstant bleibt. Eine solche Ände­rung des magne­tischen Flusses kann man somit dadurch erreichen, indem eine Leiter­schleife in dem Magnet­feld geschwenkt wird.

Grafik (wird später eingefügt)

Wenn zum Beispiel die Leiter­schleife in einem magne­tischen Feld um 90° geschwenkt wird, streift das magne­tische Feld jetzt nur noch parallel entlang. Da in diesem Fall das magne­tische Feld, obwohl konstant, nicht mehr durch die Fläche der Leiter­schleife hindurch­tritt, kommt es zu einer erheb­lichen Ände­rung des magne­tischen Flusses. Und bereits dadurch kann eine Induktions­spannung beobachtet werden. Auf dieses Art und Weise lassen sich Spannungen erzeugen, wie das bei einem Generator der Fall ist.

Hierzu möchten wir gedanklich eine Versuchs­anordnung betrachten. Nehmen wir an, wir haben einen Leiter­kreis oder eine Spule, bestehend aus mehreren solcher Leiter­kreise mit offenen Leiter­enden. Wenn man jetzt einen Stab­magneten hinein­schiebt, wird dadurch eine Ände­rung des magne­tischen Feldes verursacht, sowie eine Ände­rung des magne­tischen Flusses durch die von dem Leiter­kreis umschlossene Fläche. Wodurch letzt­lich eine Spannung induziert wird.

Wenn es sich dagegen um eine geschlossene Spule handelt, wird aufgrund dieser Induktions­spannung in der Spule ein Strom zu fließen beginnen. Aller­dings spricht man dabei nie von einem induzierten Strom, sondern nur von einer „induzierten Spannung”. Ob jedoch wirk­lich ein Strom fließt, hängt somit von den Verhält­nissen ab, also ob ein Leiter­kreis geschlossen ist oder offen.

Wenn aber ein Strom zu fließen beginnt, wird seiner­seits ein Magnet­feld entstehen. Als Folge davon wird der Stab­magnet das Magnet­feld spüren. Nun wird es so sein, dass der Stab­magnet entweder durch das Magnet­feld noch mehr beschleunigt wird oder es wird ihn abbremsen. In diesem Fall wird das Magnet­feld den Stab­magneten wegen der Energie­erhaltung abbremsen.

Insofern wird ein Teil seiner kinetischen Energie in eine andere Energie­form umge­wandelt. Da die Spule einen gewissen Ohm'schen Wider­stand hat, und der Strom zu fließen beginnt, wird er den Leiter aufwärmen. Diese frei­gesetzte Wärme, entspricht genau der Energie, die dem Magneten entzogen wurde.

Diese Behinderung in der Bewegung des Stab­magneten wird durch die Lenz'sche Regel definiert.

Die „Lenz'sche Regel” besagt, dass die induzierte Spannung zu einer Behinde­rung des induzie­renden Vorgangs führt. Es ist aber nicht die induzierte Spannung selbst, die diesen Vorgang behindert. Sondern die Spannung hat zunächst den Strom zur Folge. Der Strom seiner­seits bewirkt ein Magnet­feld. Und das Magnet­feld behindert schließlich den Stabmagneten.

In allen Fällen geht es um die induzierte Spannung längs eines Leiter­kreises. Hier reicht die Definition der Spannung, „Spannung ist Potential­differenz”, nicht mehr aus. Zutref­fender ist vielmehr, dass die elek­trische Spannung „Arbeit pro Ladungs­einheit” ist.

Demnach gilt für die induzierte Spannung:

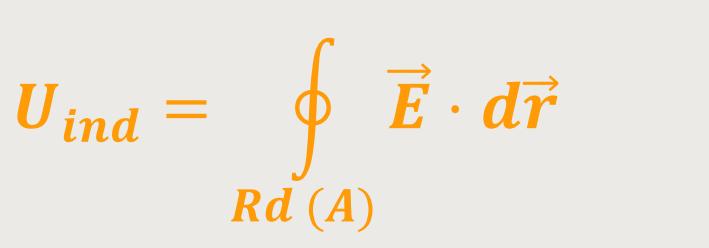
Bei diesem Formalismus geht es nicht um Potenziale oder Potenzial­differenzen. Denn wenn dieses Ring­integral ≠ null ist, dann hat man nicht mehr die Situation, dass das Integral längs jeder geschlossenen Kurve = Null ist. Daher ist das elek­trische Feld, um das es hier geht, kein konser­vatives Feld. Es geht daher um eine Fläche A, die von dem Leiter umschlossen wird.

Für den magnetischen Fluss gilt:

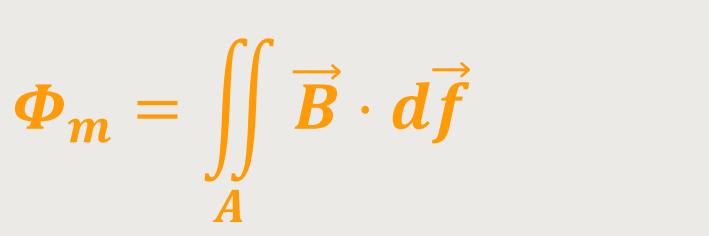
Es geht demnach um eine elek­trische Spannung und einen magne­tischen Fluss.

Grafik (wird später eingefügt)

Im Grunde geht es um eine Spannung längs des gesamten Leiter­kreises. Die -Vektoren in dem Leiter­kreis sind für die Spannung verant­wortlich, und rufen einen elek­trisches Wirbel­feld hervor, der zu der Induktions­spannung führt.

Daraus ergibt sich das Faraday'sche Induktions­gesetz:

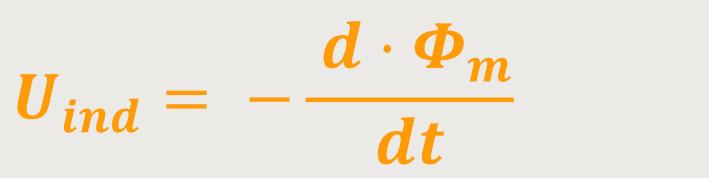
Wie verhält es sich mit dem Zeitintegral?

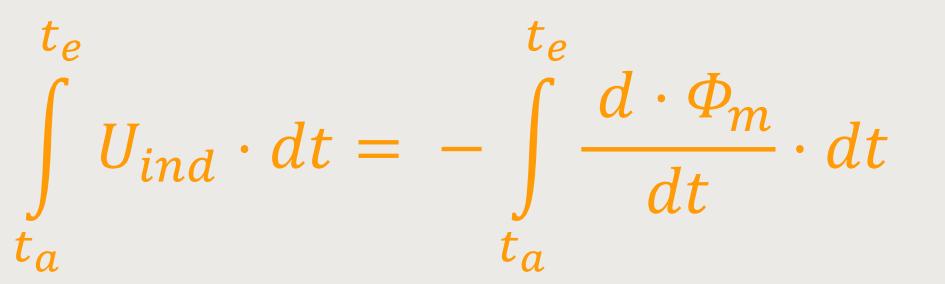
Diese Beziehung lässt sich durch Substitution umformen, und mit anschlie­ßender Integration erhält man:

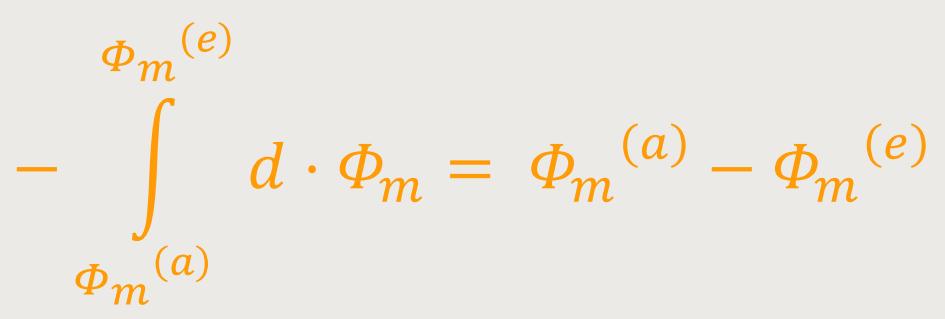
Am Anfang und am Ende hat der magne­tische Fluss ϕ_m einen bestimmten Wert. Daher wird die Differenz immer konstant sein, wobei die Änderungs­geschwindig­keit keine Rolle spielt.

Jetzt gibt es aber einen interes­santen Zusammen­hang zwischen dem Induktions­gesetz und der Lorentz-Kraft. Bei der Lorentz-Kraft war es ja so, wenn man einen Ladungs­träger in einem magnetischen Feld bewegt, wird eine Kraft auf den Ladungs­träger ausgeübt.

Grafik (wird später eingefügt)

Was das mit nun dem Induktions­gesetz zu tun hat, zeigt folgende Überlegung:

Hierzu stellt man sich gedank­lich eine recht­eckige Leiter­schleife vor. Ein konstantes äußeres Magnet­feld tritt durch diese Schleife hindurch. Des Weiteren nehmen wir an, dass die Leiter­schleife veränder­lich ist. Deshalb ist ein elek­trischer Schleif­kontakt ange­schlossen, der sich auf der Schleife bewegen lässt. Die Fläche, die von der Leiter­schleife einge­schlossen wird, definieren wir mit l · b.

Der Schleif­kontakt wird sich mit einer Geschwindig­keit bewegen. Aufgrund der Geometrie sind drei Teile des recht­eckigen Leiters in Ruhe und nur ein Teil bewegt sich. Wenn nun eine Kraft auf den beweg­lichen Schleif­kontakt ausgeübt wird, werden sich die Ladungs­träger zu bewegen beginnen. Und wenn diese Leitungs­elektronen in dem magne­tischen Feld bewegt werden, wirkt senkrecht zu beiden eine Kraft. Aufgrund dessen wird in der Schleife eine Spannung auftreten und dement­sprechend ein Strom fließen.

Anderer­seits lässt sich das auch aus Sicht des Induktions­gesetzes auffassen. Hierzu betrachten wir die gleiche Geometrie. Die Leiter­schleife bewegt sich jetzt flexibel in einem konstanten Magnet­feld. Dadurch, dass man den Schleif­kontakt verschiebt, verändert man die Fläche und damit auch den magne­tischen Fluss, welcher durch die Fläche hindurch­tritt. Und in ähn­licher Weise wird ein Strom zu fließen beginnen.

Die Eckpunkte des Schleif­kontakts bezeichnen wir mit P und Q. Die beiden anderen Eckpunkte der Fläche mit R und S. Nun werden wir die Lorentz-Kraft dem Induktions-Gesetz gegen­über­stellen und unter­suchen, ob es einen Zusammen­hang gibt.

Zunächst unter­suchen wir obige Geometrie anhand der „Lorentz-Kraft” und betrachten insbe­sondere das Leiter­stück PQ. Dieses Leiter­stück (Schleif­kontakt) wird mit der Geschwindig­keit bewegt. Als Folge davon wirkt eine Lorentz-Kraft auf eine Ladung q. Weil alles senk­recht zueinander ange­ordnet ist, lässt sich die Kraft skalar beschreiben. Die Kraft lässt sich definieren als:

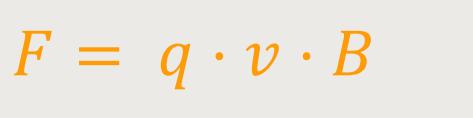
Die Kraft aus Sicht des Schleif­kontakts lässt sich auch inter­pretieren. Wenn in einem Leiter eine Kraft­wirkung auf die Ladungs­träger entsteht, dann wird der Leiter das so inter­pretieren, als wenn aus seiner Sicht ein elek­trisches Feld vorhanden ist. Dieses elek­trische Feld führt zu dieser Kraft­wirkung. Und dieser Kraft­wirkung entspricht ein elek­trisches Feld E .

Daraus folgt:

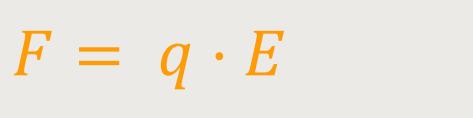
Durch Einsetzten erhält man für das elektrische Feld:

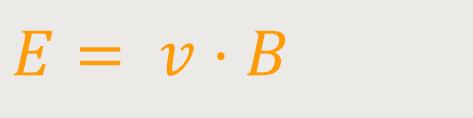
Bezogen auf die Spannung ergibt sich:

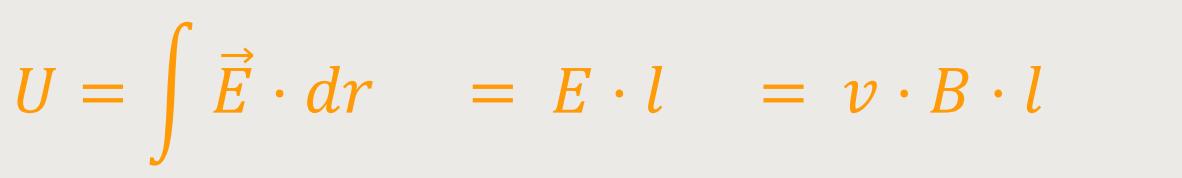
l   ist der Abstand zwischen P und Q

Um das  Induktions­gesetz” verwenden zu können, benötigt man den magnetischen Fluss durch die Leiter­schleife in obigem Beispiel.

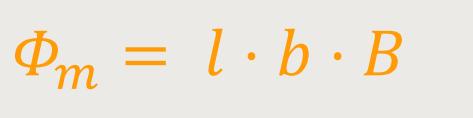
Da sich die Länge b der Leiter­schleife ändert, ergibt sich daraus für den magne­tischen Fluss:

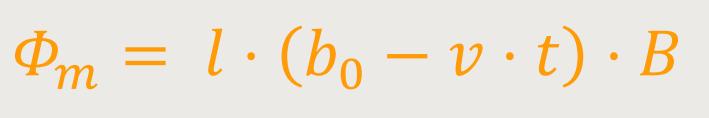
Durch Differen­tiation nach t erhält man:

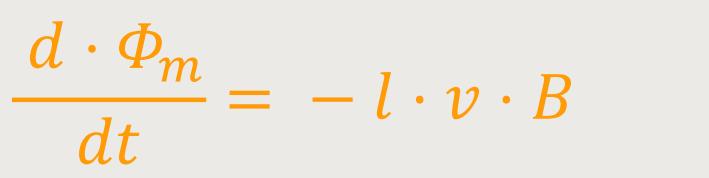
Unter Anwendung des Induktions­gesetzes ergibt sich::

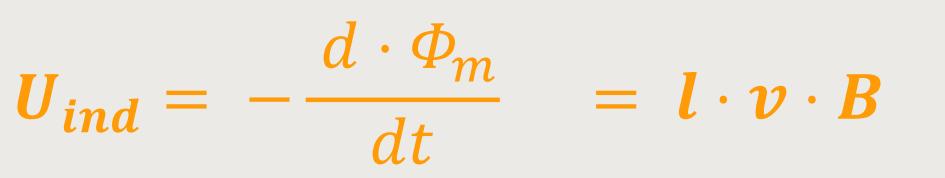
Und damit kommt in beiden Fällen (s.o.) das Gleiche heraus.

Abschließend lässt sich Induktions­gesetz noch umformen in eine differen­tielle Form.

Die Spannung in einer geschlossenen Leiter­schleife (s.o.) ist definiert als:

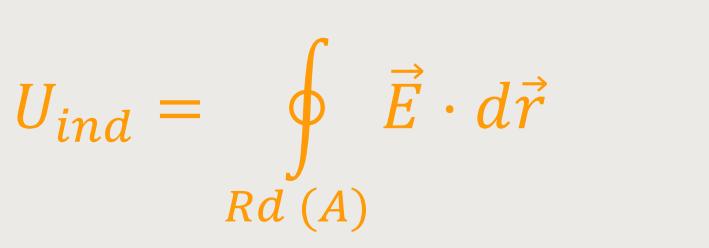
Nach dem Stokes'schen Integral­satz lässt sich das auch umformen und als Flächenintegral schreiben:

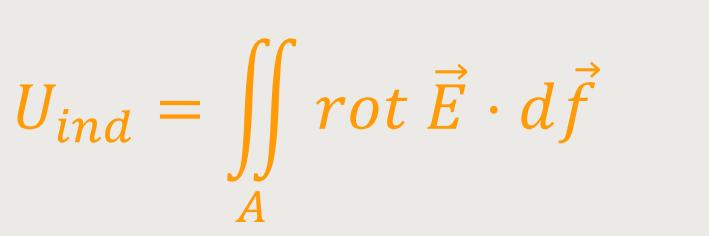
Andererseits gilt für das Flächen­integral des magne­tischen Flusses (s.o.):

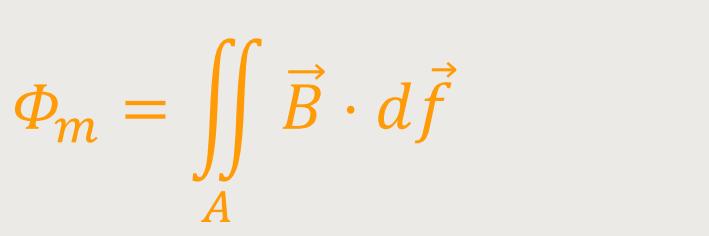
Wenn dieses Flächen­integral nach der Zeit abge­leitet wird, folgt daraus:

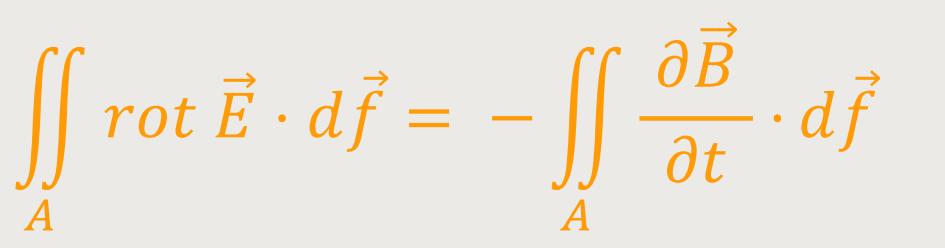
Da diese Beziehung für alle beliebigen umschlossenen Flächen gelten soll, gilt es auch für die Integranden. Und damit erhält man:

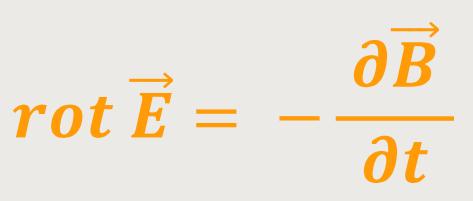
Und das ist die 4. Maxwell-Gleichung.

Somit haben wir aus dem Induktions­gesetz die 4. Maxwell-Gleichung erhalten. Hierbei handelt es sich wieder um eine homogene Gleichung. Diese Maxwell-Gleichung sagt im Wesent­lichen aus, dass eine zeit­liche Änderung des magne­tischen Feldes zu einem elek­trischen Wirbel­feld führt.

⇦ Kapitel Kapitel ⇨